具有避难所的非自治差分修正Leslie－Gower捕食－食饵系统的动力学行为研究

陈婉琳，龚晓杰，赵亮，张惠英

(福州大学数学与计算机科学学院，福建福州 350116)

0 引言

近年来，学者们研究了具有避难所的捕食－食饵系统［1－4］，发现避难所对系统动力学行为的影响较为复杂．吴玉敏等［4］研究了一类具有避难所和修正Leslie－Gower项的非自治捕食－食饵系统，发现避难所的增大有利于系统的持久发展．而由于其它食物来源的存在，捕食者种群恒持久，且捕食者种群密度随着其他食物来源的增大而增大，从而间接的对食饵种群产生不利影响．考虑到对于生命短世代不重叠的种群或是数量较少的生命长世代重叠的种群用差分方程表示更为合理，在文［4］的基础上，我们研究如下差分系统:

其中:x(n)，y(n)分别表示食饵和捕食者的种群数量;a(n)，b(n)，c(n)，r1(n)，r2(n)，k(n)，q(n)均为有正的上下界的非负序列，a(n)，r1(n)分别表示食饵和捕食者的内禀增长率，b(n)为食饵种群的密度制约因素，c(n)表示捕获率，k(n)衡量了捕食者除食饵之外的其他食物来源的丰富程度，q(n )(0≤q(n)＜ 1)为食饵避难所的最大容纳量，q(n)x数量的食饵躲进避难所， (1－q(n))x数量的食饵可被捕食者捕获．根据生物学意义，假设系统(1)满足初始条件x(0)＞0，y(0)＞0，从而易知，对于任意n≥0，都有x(n)＞0，y(n)＞0．本文的目的旨在通过对差分系统(1)的动力学行为进行详细探讨．

此外，对于任一非负有界序列{f(n)}，定义:

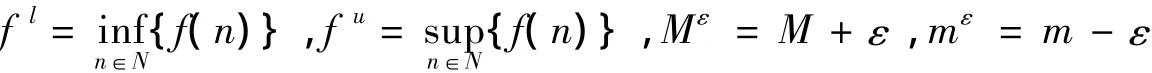
1 持久性

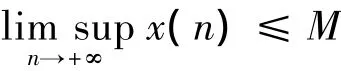
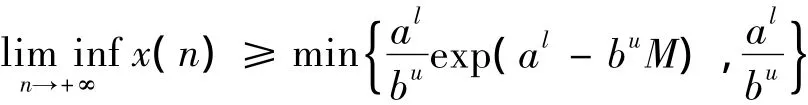
定理1 假设条件

成立，则系统(1)是持久的．

证明 设 (x(n)，y(n))T为系统(1)的任一正解，类似文［2］中定理2．3的证明，可以得到:

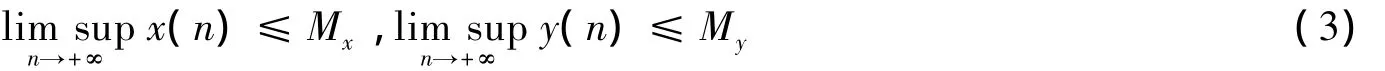
根据引理1知:

所以

于是，有:

令ε→0，有:

由系统(1)的第二个方程有:

根据引理1得:

通过计算，可知:

所以，有:

令ε→0，有:

根据(3)，(4)和(6)式可知，在(2)条件下系统(1)是持久的．定理证毕．

2 全局稳定性

定理2 在条件(2)成立的前提下，进一步假设条件:

成立，则系统(1)的正解是全局渐近稳定的．

证明 设 (x(n)，y(n))T， (x*(n)，y*(n))T是系统(1)的两个正解，令:

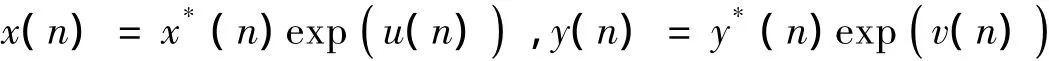
利用中值定理，则系统(1)等价于:

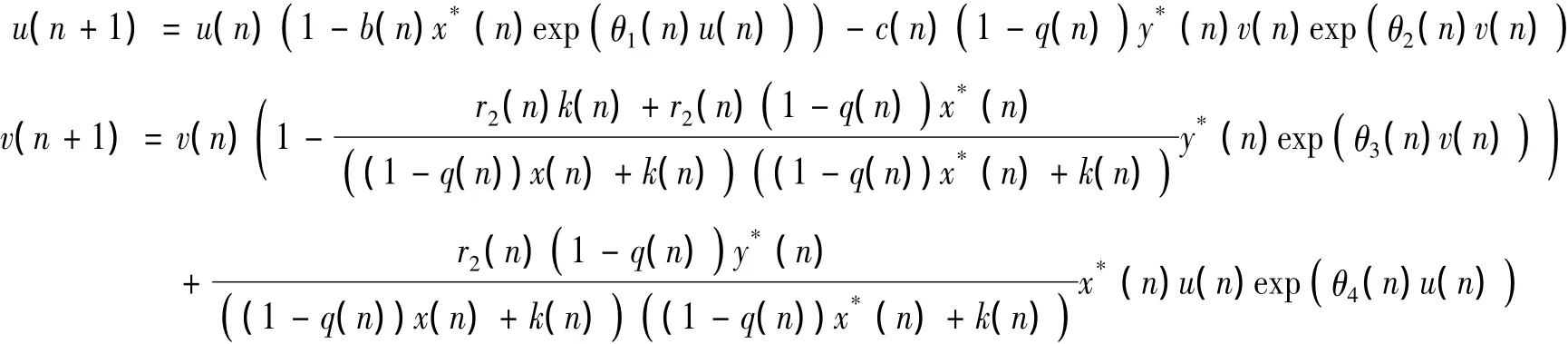
这里，θi(n)∈(0，1)(i=1，2，3，4)．要证明定理的结论成立，只需证明nlim+u(n)=0，nlim+v(n)=0．→∞→∞

由条件(7)，存在足够小的ε＞0，使得:

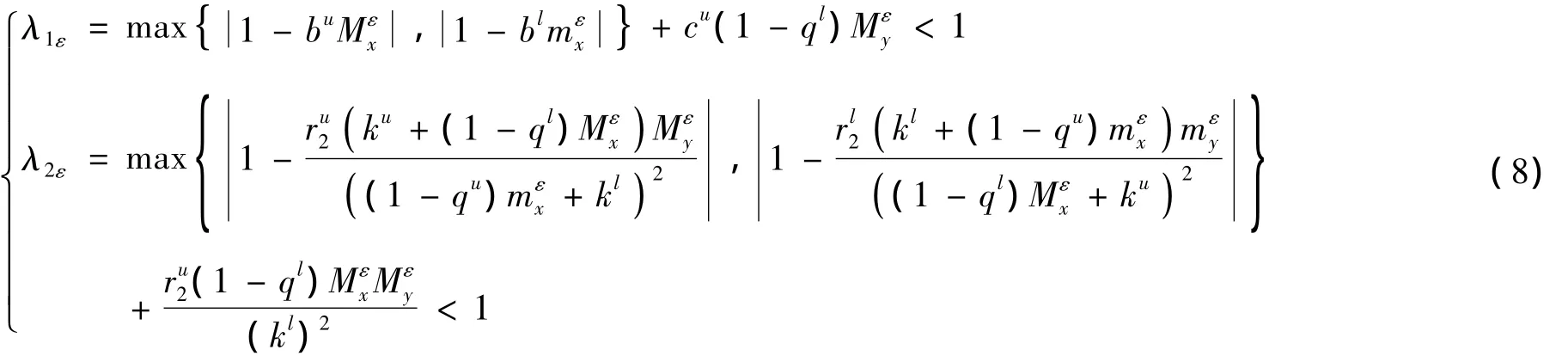
对于上述ε＞0，根据定理1，存在N2＞N1，当n≥N2时，有:

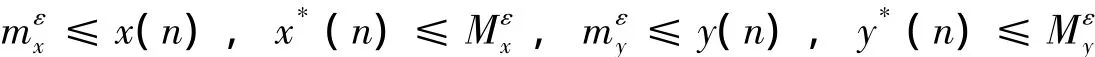
又因为θi(n)∈ (0，1)(i=1，2，3，4)，所以，x*(n)exp(θi(n)u(n))(i=1，2)在x*(n)和x(n)之间，y*(n)exp(θj(n)v(n))(j=3，4)在y*(n)和y(n)之间．从而，由(8)式得，

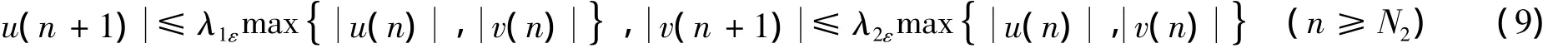
再令 λ =max{λ1ε，λ2ε}，由(9)式，有:

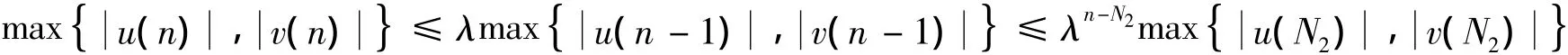
从而得到nlim+u(n)=0，nlim+v(n)=0．定理证毕．→∞→∞

3 食饵种群的绝灭性和捕食者种群的稳定性

定理3 假设条件

和条件

成立，则

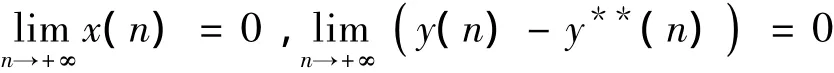
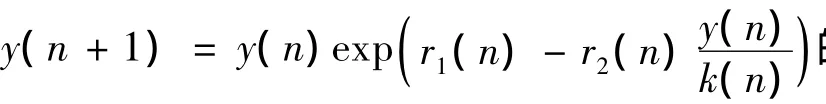
证明 由条件(10)可知，au－cl(1－qu)my＜0，从而可取到足够小的正数ε和δ，使得au－cl(1－qu)mεy＜ －δ＜ 0．设 (x(n)，y(n))T是系统(1)的任一正解，根据定理1，对于上述ε，存在N3＞N1，当n≥N3时，有y(n)≥mεy．故由系统(1)的第一个方程得:

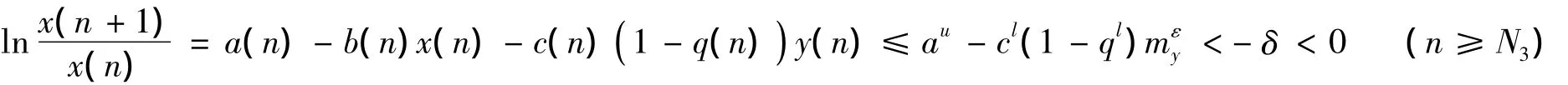
对上式从N3到n求和，得

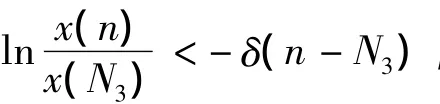
令 y(n)=y＊＊(n)exp(v(n)) ，利用中值定理可得，系统(1)的第二个方程等价于:

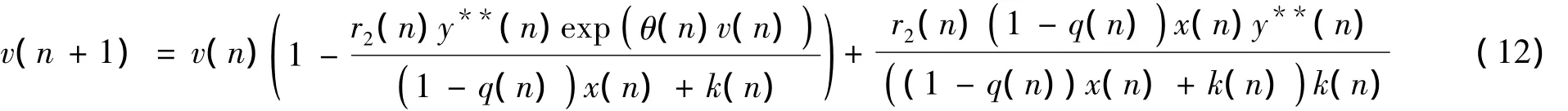
也就是:

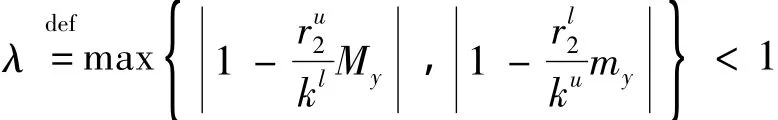
则可选取任意小的ε'＞0，使得:

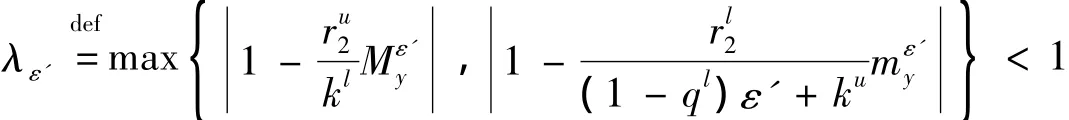
对于上述ε'，根据nlim+x(n)=0以及定理1，存在充分大的N4＞N3，当n≥N4时，有:→∞

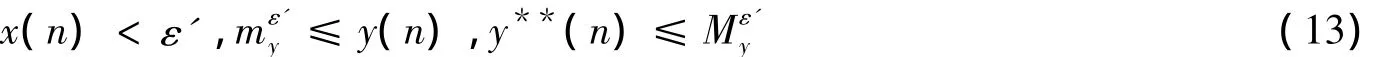
由于 θ(n)∈ (0，1)，所以 y＊＊(n)exp(θ(n)v(n)) 在y＊＊(n)和y(n)之间．由(12)和(13)式可得:

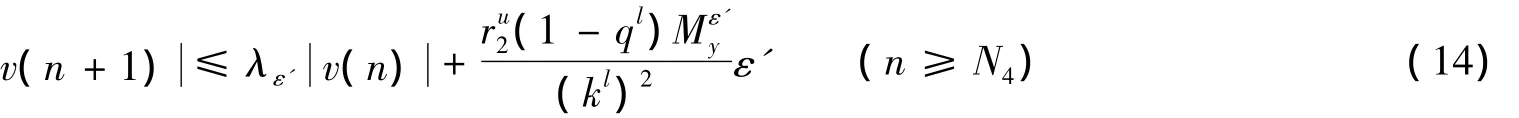
由(14)式，有:

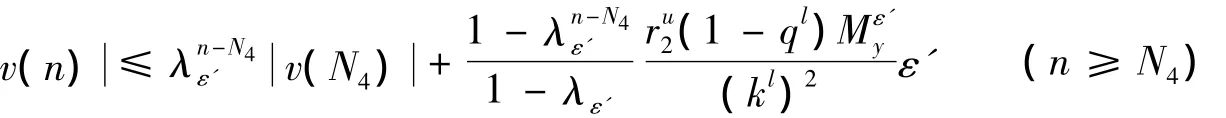
由于λε'＜1，并且ε'任意小，由上式可得nlim+v(n)=0．定理证毕．→∞

4 结语

研究具有避难所的非自治差分修正Leslie－Gower捕食－食饵系统，发现其他食物来源对系统的持久性起重要作用．由于捕食者种群具有其他的食物来源，捕食者种群恒持久，这与文［4］中所得的结果一致．同时，建立足够大的避难所就能保证食饵种群持续生存．也就是说，足够大的避难所确保了系统的持久发展，这与Lotka－Volterra模型中，避难所过大时，捕食者种群会由于缺少食物而绝灭的结论有所不同．此外，我们还进一步研究了系统的绝灭性，发现当避难所较小时，食饵种群由于捕食者的捕食而最终绝灭，但此时捕食者种群由于拥有其他的食物来源仍可以稳定振荡的形式存在．通过以上研究发现，对捕食者种群而言，多食性捕食者由于食物来源丰富能获得更好的生存机会，这是单食性物种无法比拟的;对食饵种群而言，建立足够大的保护区是确保其持续生存的重要手段．