修正q－Phillips算子的逼近性质

任美英，曾亮

(1．武夷学院数学与计算机学院，福建武夷山 354300;2．厦门大学数学科学学院，福建厦门 361005)

0 引言

自1997年Phillips［1］提出并研究q－Bernstein算子以来，q－微积分在逼近论中的应用成为了一个研究热点，很多逼近论方向的专家学者致力于该领域的研究，获得了许多很好的结果，如文献［2－6］．2011年，Yüksel［7］研究了q－Phillips算子的逼近性质．提出修正的q－Phillips算子，并研究修正q－Phillips算子的逼近性质．

首先，引入q－整数和q－微积分的若干概念，这里所述的概念详细可见文献［8－12］．对任意固定的实数q＞0和非负整数k，q－整数和q－阶乘分别定义为:

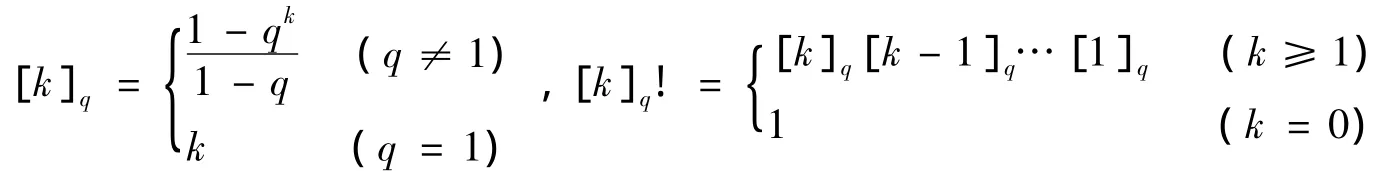
两个q－模拟指数函数分别定义为:

q－Jackson积分和q－广义积分分别定义为:

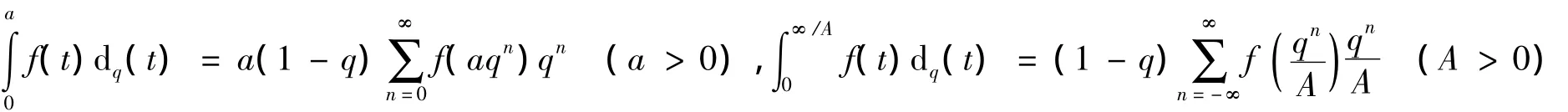
假设级数绝对收敛．对t＞0，q－Gamma函数定义为:

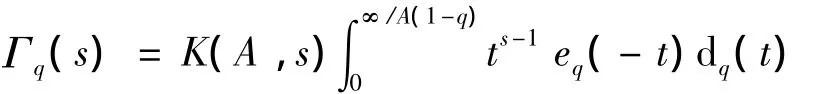
1 算子的构造

设f∈C［0，∞)，q∈(0，1)，x∈［0，∞)，n∈N，文献［7］定义了如下q－Phillips算子:

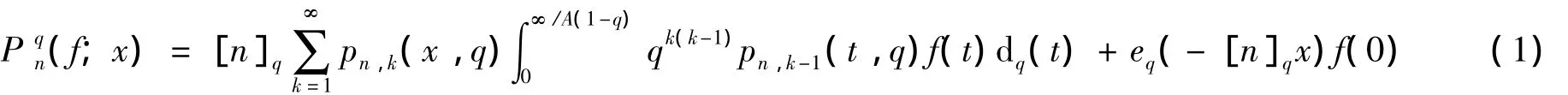
其中:

可以计算得到算子Pqn(f;x)的如下各阶矩量(见文献［7］)．

引理 1［7］对式(1)给出的算子Pqn(f;x)，让 em(t)=tm，m=0，1，2，3，4，则

由引理1知，算子Pqn(f;x)只保持常数．为了提高算子列{Pqn(f;x)}的收敛速度，可以将它进行修正，使得修正后的算子能保持线性函数．

设f∈C［0，∞)，q∈(0，1)，x∈［0，∞)，n∈N，定义修正的q－Phillips算子如下:

其中:pn，k(x，q)由(2)式给出．

引理2 对(3)式定义的算子~Pqn(f;x)，让em(t)=tm，m=0，1，2，3，4，则

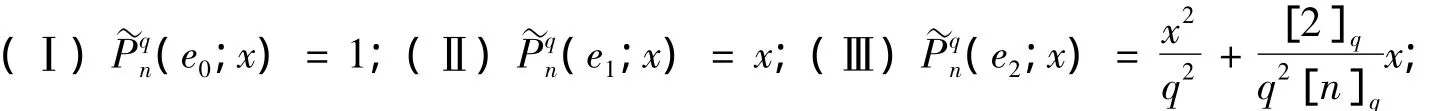
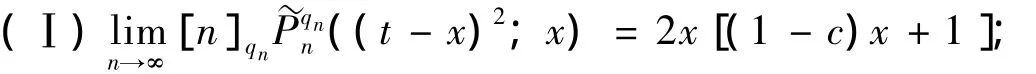
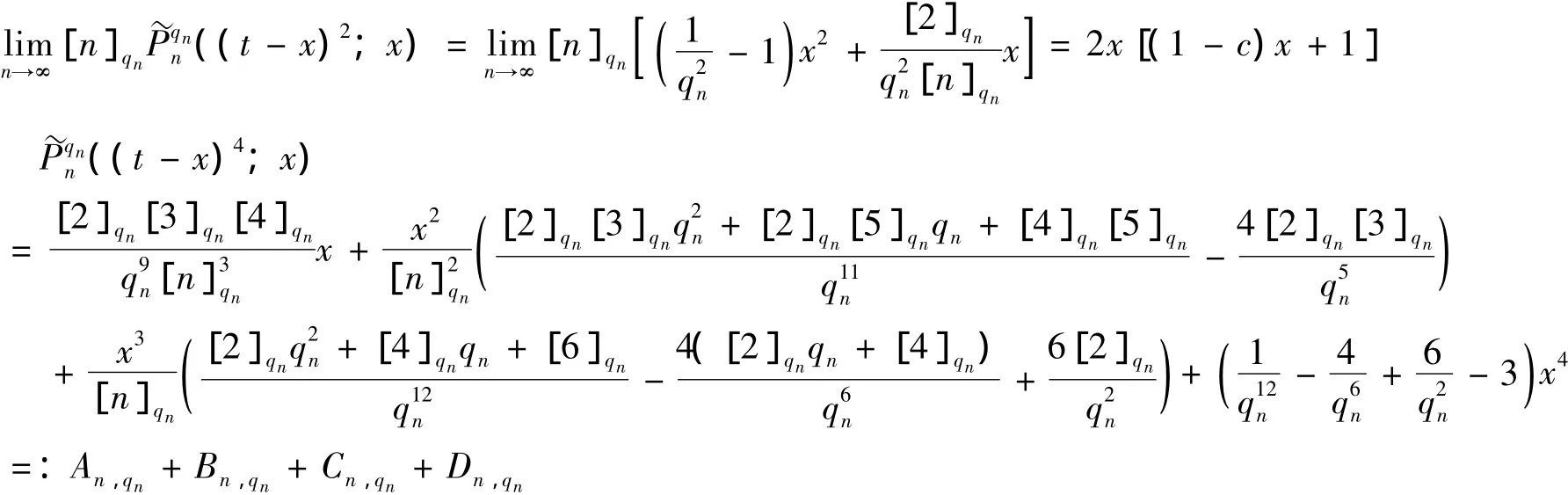
基于qn∈(0，1)，=1时，由n→∞ 可得［n］qn→∞(见文献［13］)和，易知，

2 主要结果及其证明

定理1 设qn∈(0，1)，则对任意f∈C2*［0，∞)，序列{(f;x)}在区间［0，A］上一致收敛于f当且仅当=1．

另一方面，若对f∈C2*［0，∞)，序列{(f;x)}在［0，A］上一致收敛于f，则=1．事实上，若不然，注意到qn∈(0，1)，则必存在一个子列{qnk}⊂(0，1)，使得=q0∈［0，1)，这样，这表明序列{(f;x)}在［0，A］上非一致收敛于f，与已知矛盾．因此，=1．定理证毕．

定理2 设序列{qn}满足qn∈(0，1)，=1且qnn=c(c是常数)，则对任意f∈C2*［0，∞)使得f'，f″∈C2*［0，∞)，有［n］qn((f;x)－ f(x))= ［(1 － c)x+1］xf″(x)．

由Cauchy－Schwartz不等式，有

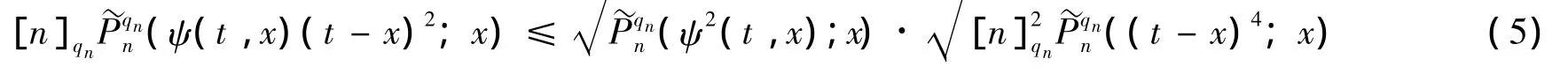
在此还应特别提及各级教研组织的力量．例如，中国特有的“教研员”在这方面就具有特别重要的作用：“中国有专门的包含省、地（市）、县（区）等各级教研室的教研工作管理系统，这个系统中的教研员通过有计划的、形式多样的教研活动，组织不同层级的课例研究，从而为中国教师专业发展提供有效支持．”[9]

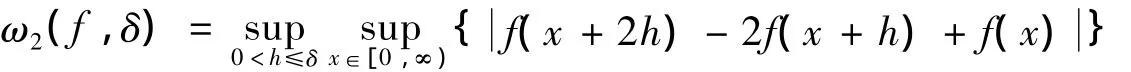
由文献［15］有:

其中:c是一个正常数．

定理3 设q∈(0，1)，f∈CB［0，∞)，则对任意的x∈(0，∞)，有:

其中:c是一个正常数．

证明 设g∈W2，x∈(0，∞)，由泰勒公式知，

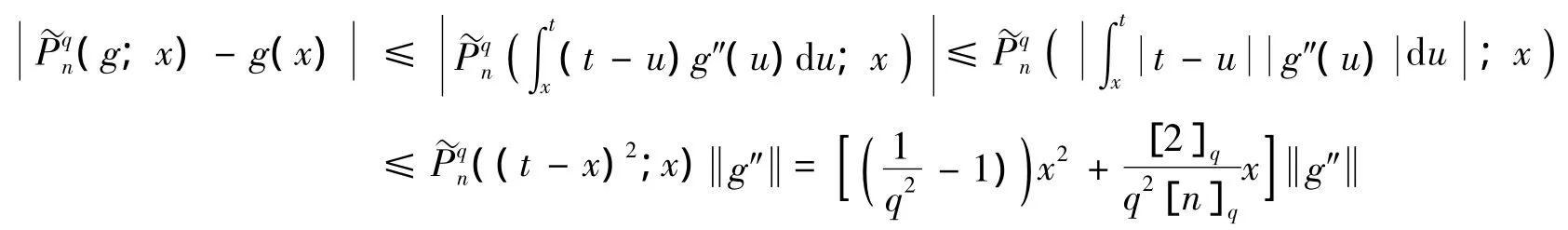
因为对f∈CB［0，∞)，n∈N和x∈(0，∞)，由式(3)和引理2可得:

因此，有:

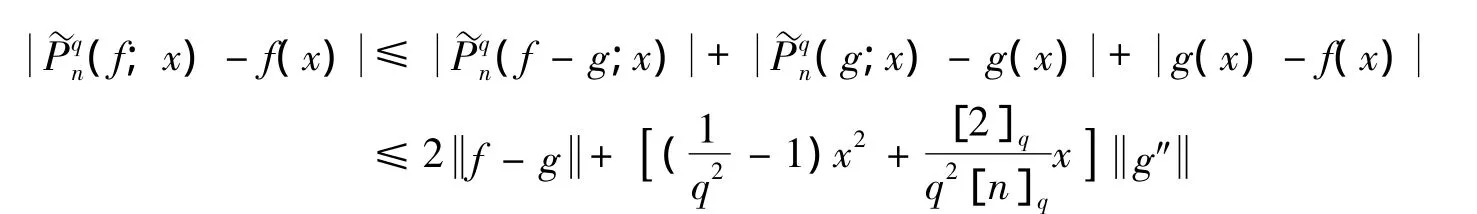
对上式右边关于g∈W2取下确界，有:

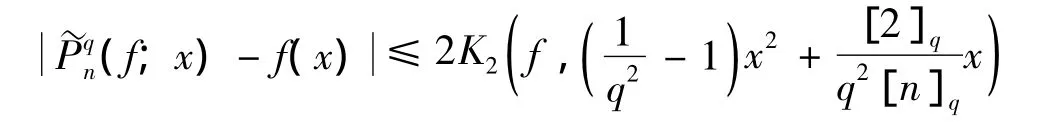
从而由式(6)知，存在常数c＞0，使得:

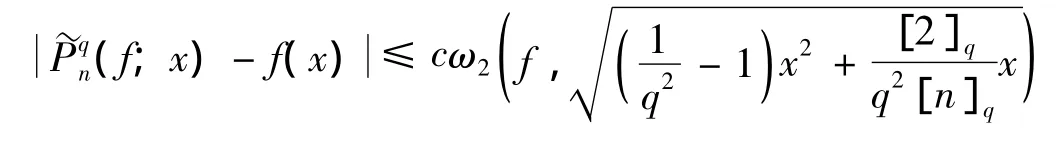
定理证毕．