一类四阶微积分方程的有限元逼近

任全伟，庄清渠

(1．上海师范大学数理学院，上海 200234;2．华侨大学数学科学学院，福建泉州 362021)

0 引言

很多数学物理问题的研究最终都可归结为微积分方程的研究．人们也一直在用微积分方程模型来解释和预知各种自然现象．然而只有少数比较简单的微积分方程能够用初等解法进行求解．大部分由实际问题建模得到的微积分方程往往具有比较复杂的形式，要找出解的解析表达式是比较困难甚至是不可能的．有些解虽然能解析表达，但表达式往往比较复杂而不切实用．况且实际问题往往也只要在一定的精度范围内求出微积分方程的解在某些点上的值，并不一定要求出它的解析表达式．因此研究微积分方程的数值解法对生产生活有着重要的现实意义，为微积分方程寻求快速有效的解法也成为当今计算数学工作者的主要工作．

在众多微积分方程的数值解法中，有限元方法是一种进行工程计算的有效方法，自20世纪50年代起，在航空航天、水利、土木建筑、机械和流体力学等方面得到了广泛的应用［1－2］．在研究长为L的悬索桥中，当竖向位移为y(x)，负重为p(x)时，可得如下方程［3］

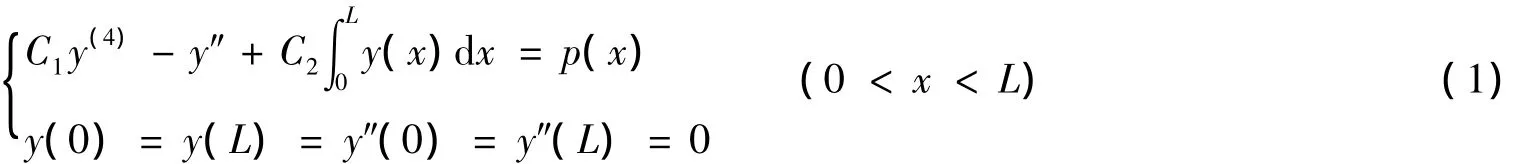
其中:C1和C2都是正常数;p(x)(≤0或≥0)是在区间［0，L］上的连续函数．为了问题的方便描述，假设在区间［0，L］上p(x)≤0．

对该四阶微积分方程，文献［4］给出了混合有限元方法的误差分析;由于对式(1)进行求解的主要难处在于非线性项的处理，文献［5－6］介绍了一种简单迭代格式来处理非线性项，并给出了有限元逼近的数值结果，但未给出误差分析．而且在计算过程中，文献［5－6］的迭代算法收敛速度不是很快，当区间分割较小时，其计算过程将会耗用大量的时间．本文将引入Newton型迭代法［7－9］对非线性项进行处理，可以较大提高迭代的收敛速度．另外，给出了有限元逼近的误差分析，最后通过数值算例来说明算法的可行性和有效性．

1 有限元逼近

记I=(0，L)，对任意1≤p≤∞，定义Lp(I)={v;vLp＜∞}，其中

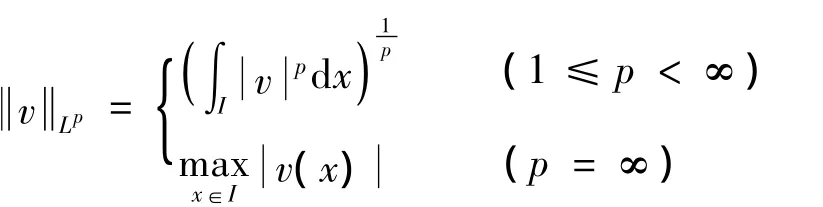
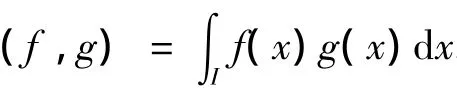
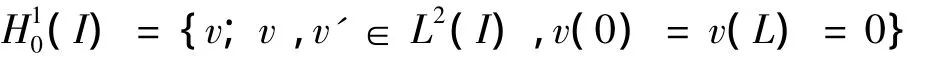
令φ=－y″，则式(1)可以写成

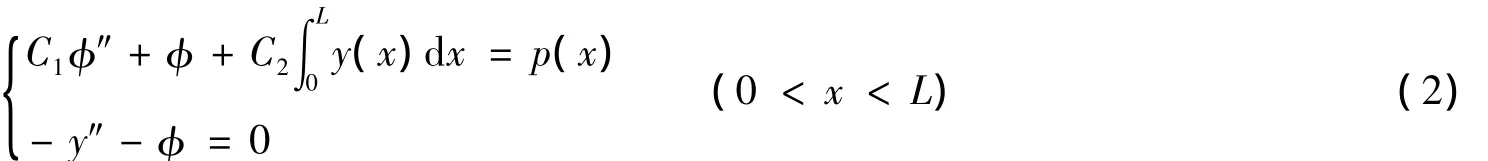
式(2)的变分形式可以写为:找(φ，y)∈H10(I)×H10(I)，使得

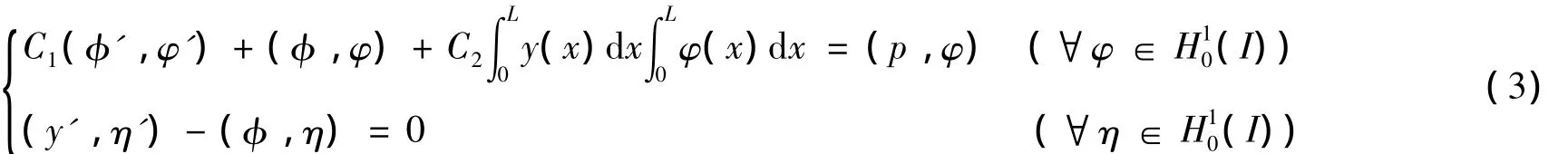
为了给出式(1)的有限元逼近形式，对区间I进行均匀剖分，令h=L/n为区间分割的长度，即

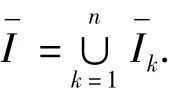
设Pm为次数不超过m的多项式空间．构造满足方程式(1)的边界条件的分片线性多项式空间X0h如下:

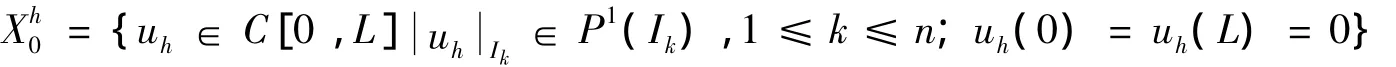
因X0h⊂H10(I)，即X0h是H10(I)的子空间．则(3)式的有限元逼近形式为:找(φh，yh)∈X0h×X0h，使得

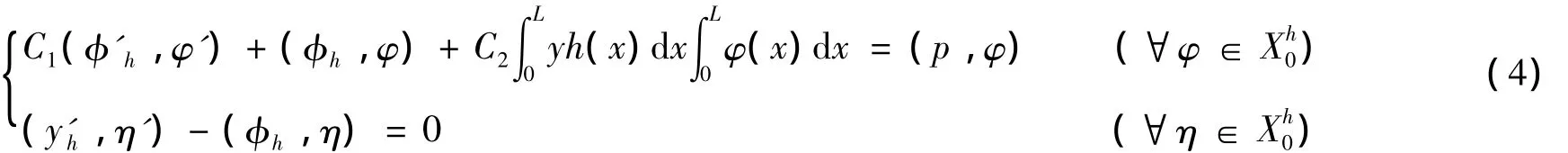
下面证明(2)式弱解的唯一性．

定理1 若(φ1，y1)，(φ2，y2)都是(4)式的解，则它们是相等的．

证明 由假设与(4)式可得

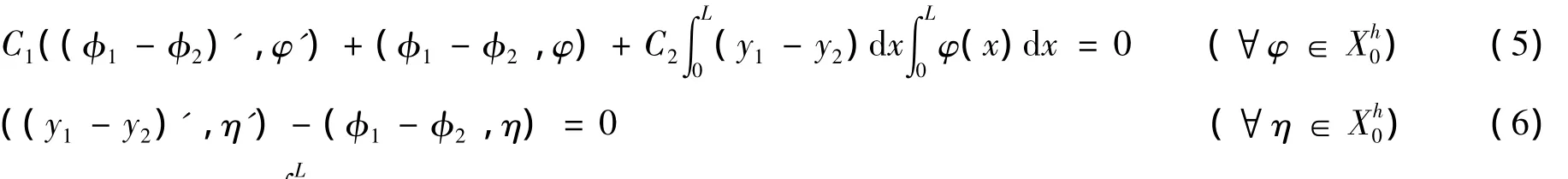
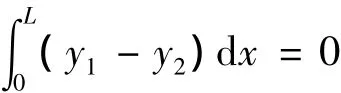
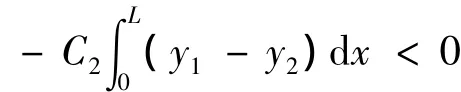
2 迭代求解

在(4)式中由于积分项的存在，直接计算将会给求解带来一些困难．因此，引入一种新的迭代格式来处理积分项．首先，记

则(4)式可等价地写为:找(φh，yh)∈Xh0×Xh0，使得

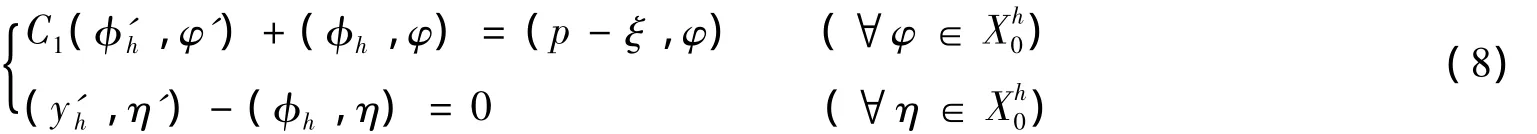
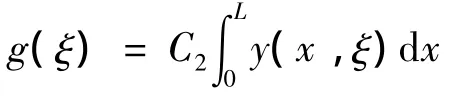
原问题的求解可归结为求解(9)式．在求解(9)式的过程中，可能会遇到下面两种情况:

1)式(9)的解析解容易求得，则由式(8)可求出式(1)的解．

2)式(9)的解析解不容易求或者求不出，则需采用牛顿型迭代算法对其数值求解，进而求解式(1)．

记f(ξ)=g(ξ)－ξ．则求解式(9)可归结为求解f(ξ)=0，其Newton迭代格式为

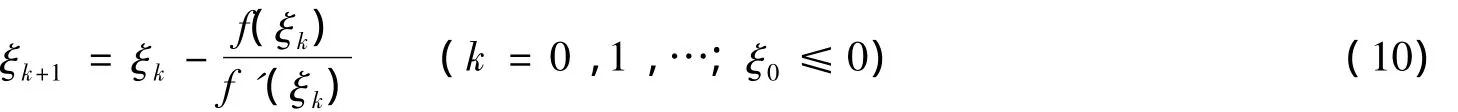
因此，式(8)的迭代计算过程是:找(φkh，ykh)∈Xh0×Xh0，使得

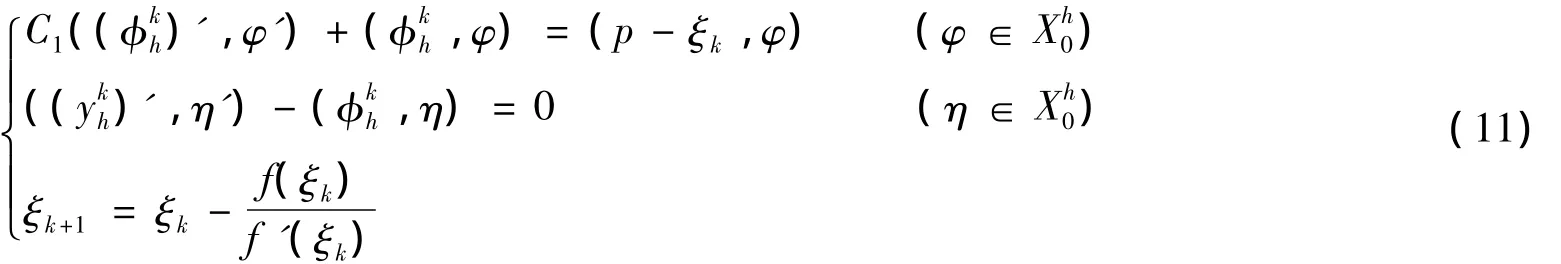
由上式可知，在迭代过程中需计算f(ξk)，f'(ξk)的值．由于f(ξk)的显式表达式通常难以求得，可采用数值积分来计算f(ξk)，即

对于f'(ξk)采用差商的形式进行替代，两种迭代格式分别称之为Newton法1，Newton法2．

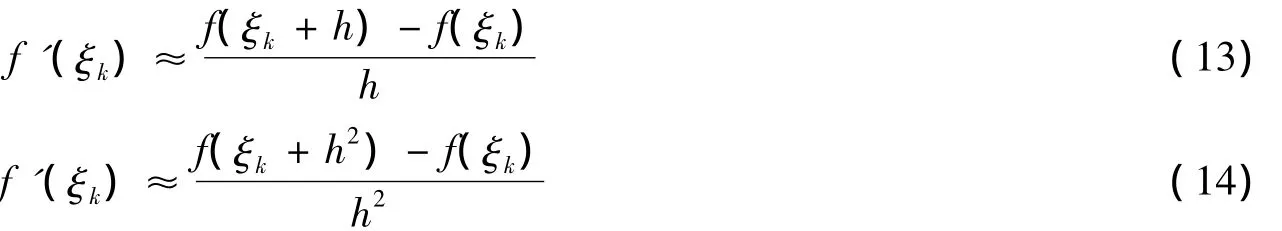
其中:h为区间分割的长度，通过求解式(11)可求得式(1)的数值解．

3 误差估计

首先，令P01，hy，φ∈X0h分别表示y，φ∈H10(I)到空间X0h上的投影算子，且定义如下:

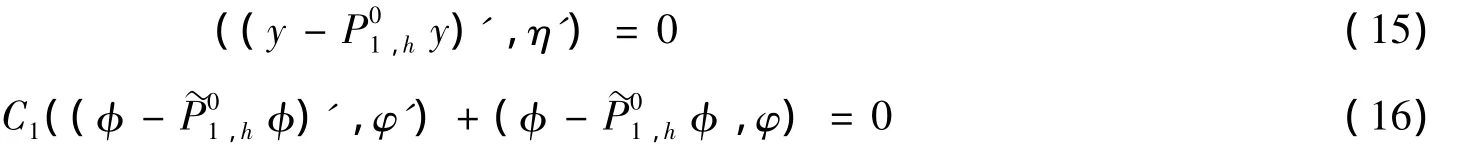
由文献［11］可知如下结论成立

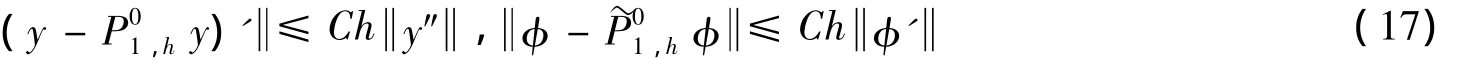
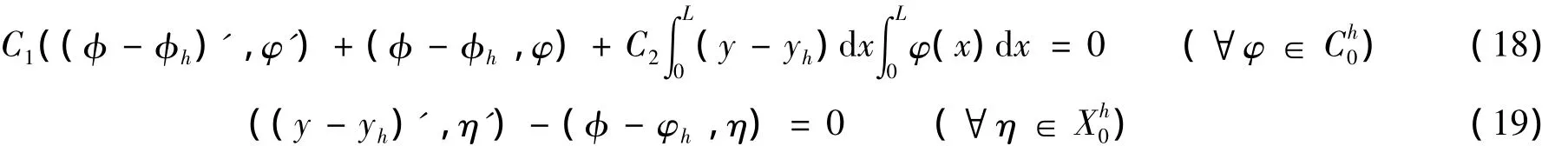
其中C是正常数．此外，由式(13)、(14)可得类似文献［12］中引理3．1的证明过程，易得如下结论．

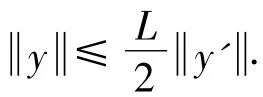
引理2 若(φ，y)，(φh，yh)分别是式(3)、(4)的解，P01，h，分别是式(15)、(16)中定义的投影算子，则可得

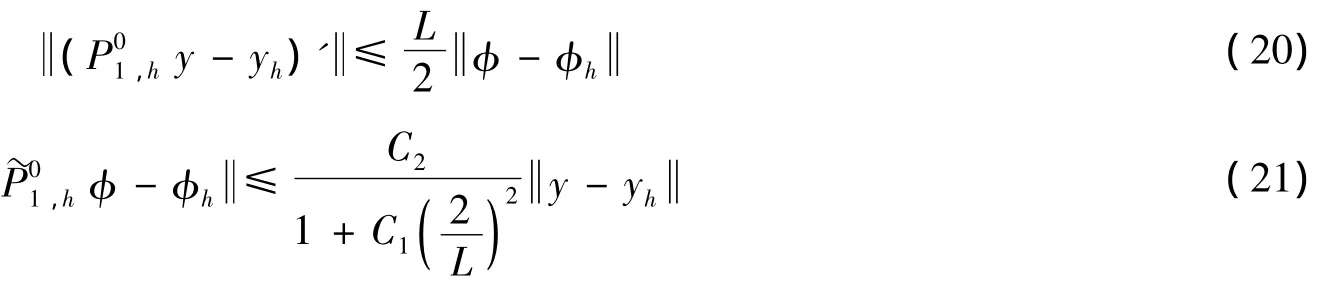
证明:对于式(20)，在式(19)中令η=P01，hy－yh，由式(15)和引理1可得

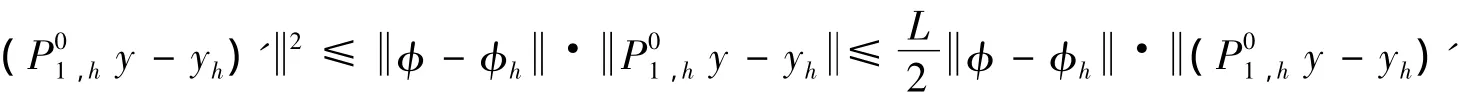
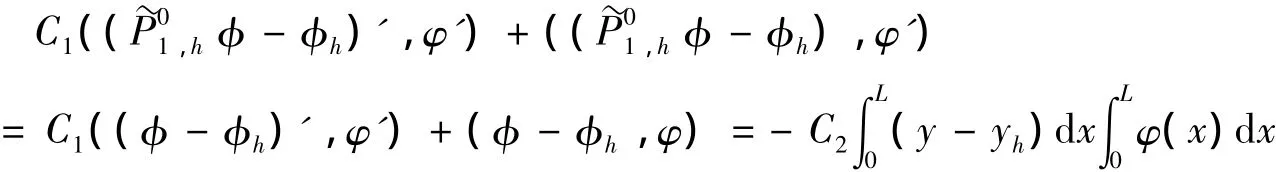
在上式中令φ =P~01，hφ － φh，由引理1可得

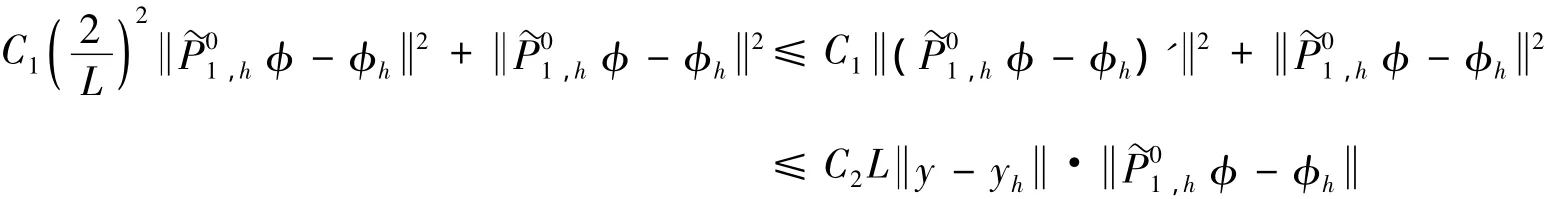
证明完毕．

这里，O(h)表示h的高阶无穷小．在证明过程中，不同式子中M可能代表不同的常数．证明 对于式(22)，由引理1，引理2和三角不等式可得:

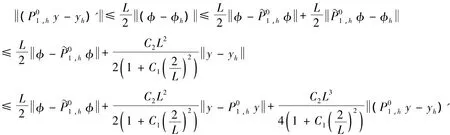
即

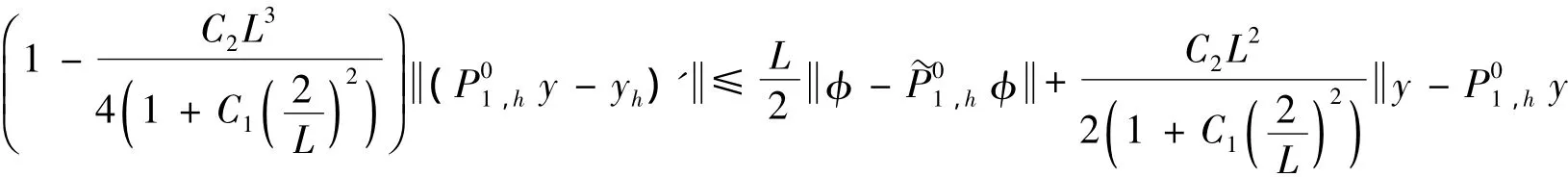
式可知:

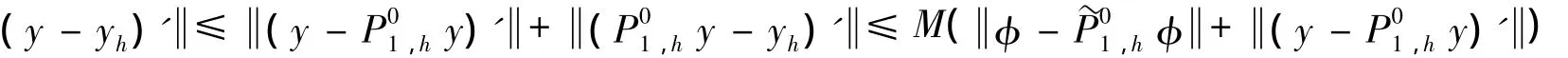
由式(17)可得 (y－yh)'=O(h)．

对于式(23)，由引理1及引理2可知

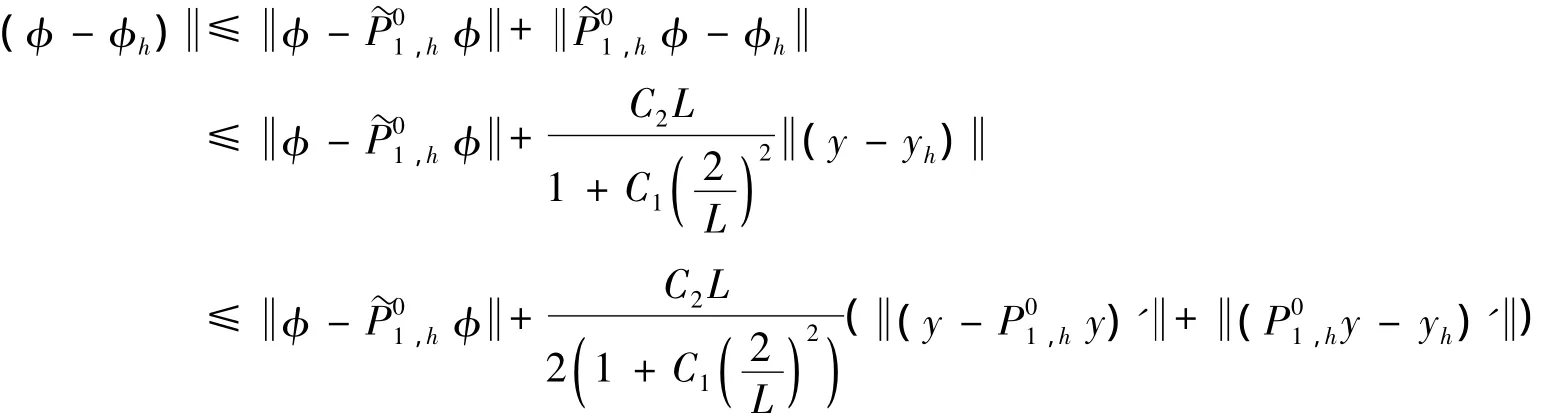
由式(17)和(22)，可得 φ－φh=O(h)，证明完毕．

4 数值结果

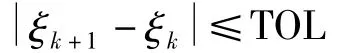
例1 p(x)=－π4sin(πx)－π2sin(πx)－2/π．此时方程式(1)的精确解为 y(x)=－sin(πx)，φ =－π2sin(πx)．

首先验证算法的收敛性．表1给出的是TOL=10－14时误差随h的变化关系．由表易见，数值解关于h平方收敛．

再取h=0．01与TOL=10－8和TOL=10－14进行计算，相应的数值结果在表2～3中给出．由表可见，在节点个数和迭代精度相同的情况下，Newton型迭代法的收敛速度比Semper迭代法快得多．但是Newton型迭代法需要求解方程(8)两次(ξk和ξk+h或ξk+h2)．

表1 TOL=10－14，Newton法1所得(例1)的数值结果Tab．1 Numerical results using Newton method 1(Example 1)with TOL=10 －14

表2 TOL=10－8，h=0．01 的数值结果Tab．2 Numerical results with TOL=10 －8 and h=0．01

例2 p(x)=11/4 －(6e+6e－1－12)/(e1－e－1)－6x，此时(1)的精确解y(x)=5x－(6ex－6e－x)/(e － e－1)+x3，φ =(6ex－ 6e－x)/(e － e－1)－ 6x．

表4～5分别给出了当TOL=10－6，h=0．01、0．001时的数值结果．由表可见，在节点个数和迭代精度相同的情况下，Newton型迭代法的收敛速度比Semper迭代法快得多．

表3 TOL=10－14，h=0．01 的数值结果Tab．3 Numerical results with TOL=10 －14 and h=0．01

表4 TOL=10－6，h=0．01 的数值结果Tab．4 Numerical results with TOL=10 －6 and h=0．01

表5 TOL=10－6，h=0．001 的数值结果Tab．5 Numerical results with TOL=10 －6 and h=0．001

在实际应用中，有时难以求得式(1)的精确解．下面从式(1)精确解未知的情况下来说明上述迭代算法的适用性．

例3 p(x)=－x2，此时式(7)的精确解难以求得．

图1，图2分别给出了当h=0．1、0．01，TOL=10－8时由Newton法1所得的数值解φh和yh

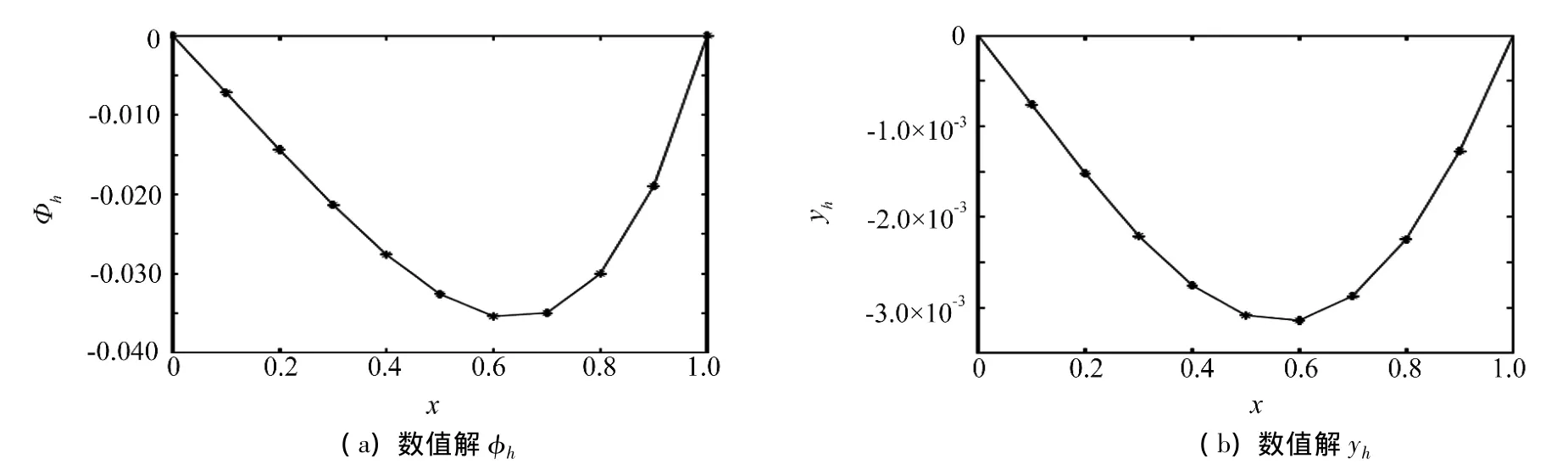
图1 h=0．1时，(φ，y)的数值解:φh，yhFig．1 Numerical solution of(φ，y)with h=0．1:φh，yh

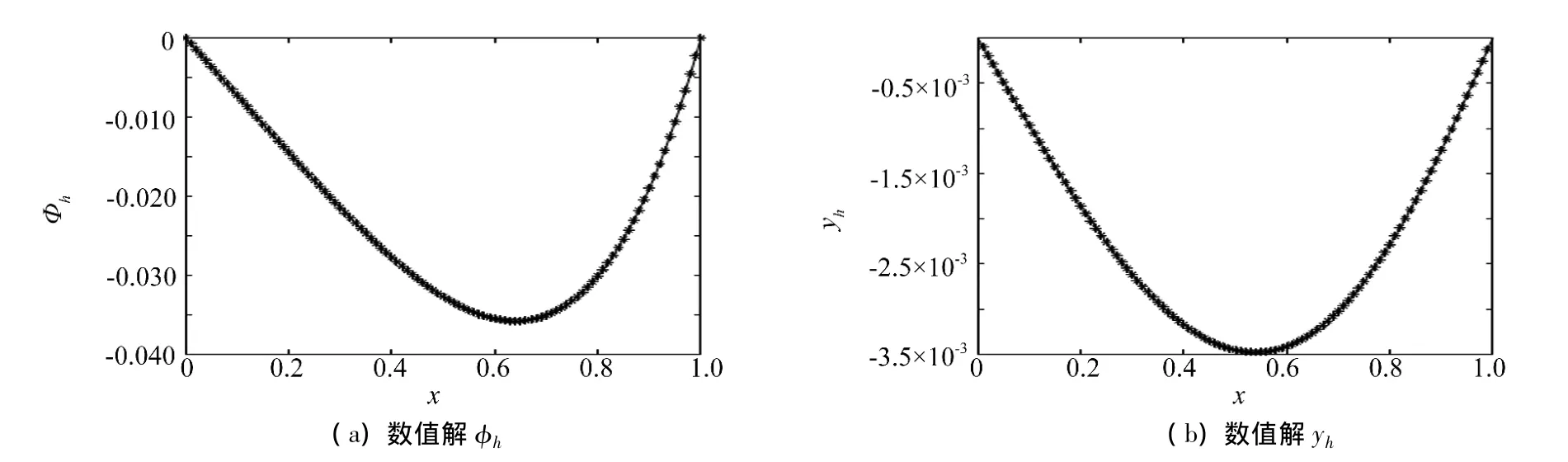
图2 h=0．01时，(φ，y)的数值解:φh，yhFig．2 Numerical solution of(φ，y)with h=0．01:φh，yh

5 结论

用逐次线性有限元和牛顿迭代法相结合数值求解四阶微积分吊桥模型．给出了详细的迭代计算过程以及误差估计．由数值结果可知:

1)采用Newton型迭代法所得的数值结果和理论分析是一致的;

2)在相同的条件下，Newton型迭代法收敛速度比Semper所采用的迭代法收敛速度快的多．需要指出的是，由于Newton型迭代法需计算式(13)或(14)值，因此在计算过程中需要求解两次方程组(ξk和ξk+h或ξk+h2);

3)迭代法可用于求解现实生活中的一些具体问题．