微积分解题中拉格朗日中值定理的运用初探

严海霞

（阜宁高等师范学校江苏盐城224000）

微积分解题中拉格朗日中值定理的运用初探

严海霞

（阜宁高等师范学校江苏盐城224000）

拉格朗日中值定理在微积分学中有着重要的地位，它建立起函数和其导数之间的关系，并且能够借助于导数的性质来推导出函数的性质，以达到对函数进行分析的目的。本文对拉格朗日中值定理在微积分解题中运用进行探讨，对其在不等式、极限以及级数收敛性的判断上的运用进行分析和归纳。

拉格朗日中值定理；微积分；运用

0.前言

在微积分学中的中值定理有着重要的地位，拉格朗日中值定理很好地把函数和其导数之间的关系联系起来，课本[1]上对其应用仅仅停留在表面，没有对其进行系统地分析和总结。因此，本文将首先对其进行简要概述，并着重对在不等式问题、求极限问题以及级数收敛性判定上如何巧妙借用其定理进行分析和研究，并给出实例加以例证。以促进对学生在学习上对该定理的掌握程度，也促进在教师之间对其的研究和交流。

1.拉格朗日中值定理概述

拉格朗日中值定理指出，假如函数f(x)具备以下两个条件：①函数f(x)在闭区间[a,b]上连续；②函数f(x)在开区间（a，b）内可导，则至少存在一点ξ，其取值范围为（a,b），可以得到:

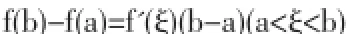
上面这个表达式给出了该定理的增量形式。将这个增量形式与在a和b之间的ξ相结合就可以在微积分中对不等式等多种题型进行解答。拉格朗日除了上面这种表达式外，还有另外几种表达形式，不同的表达形式具有不同的应用范围和作用。

（1）假如要表示曲线上某点切线斜率时，这个表达式可用式（1-1）表示：

（2）当表示函数的改变量和该函数在某一点的导数和自变量相乘的关系时，可以采用下面（1-2）这个表达形式：

（3）当表示其函数和其导数之间的关系时，可以采用下面（1-3）这个表达形式：

该定理也可以称之为中值公式或者拉格朗日公式，其作为微积分中一个重要理论，无论在学术上亦或在实际中都具有十分高的地位和研究价值，尤其对不等式证明、函数求极限以及判定级数的收敛性等问题，应用此定理，将使得需要求解的问题简单化。

在讨论该定理在微积分中的运用时候，我们必须要分析和研究其证明思路。下面对该定理的证明思路进行简要分析：

对该定理的证明思路必须引起高度地重视，因为该定理的证明思路是在不等式证明、极限求解等一切问题中应用的前提依据和重要基础。对于该定理的证明思想，可以细分为以下几个步骤：

第一，将需要证明的结论中的改为未知变量x，并借助于化简和整理后可以让等式右边为零，也即下面的（1-4）式：

第二，试图找出（1-4）式的一个原函数，其方法如下式（1-5）：

第三，f(x)就是构造出的辅助函数，再借助于罗尔定理来证明其结论的正确。

借助于罗尔定理，可以得到f(a)=f(b)，因此可以知道，f(x)在闭区间[a,b]上满足罗尔定理的条件，因此，开区间(a,b)上至少会有一点ξ，可以得到F'(ξ)=0，从而能够推导出该定理的基本公式：

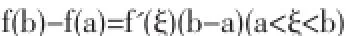
2.拉格朗日中值定理在微积分解题中的应用

2.1 拉格朗日中值定理在不等式中的应用

该定理在不等式的运用，其思想是，对于该定理公式中的ξ在开区间(a,b)中取值，不管的取得的值为多少，都能够借助于ξ在开区间(a,b)的某一值，则能够估计f'(x)的范围，或者也可以认为，在ξ是(a,b)上的取值的基础上，能够确定f'(x)取值的上下界，然后再利用f'(x)取值的最大最小值去替换该定理中的f'(ξ)，这样就很轻松地得到不等式。为此，首先应该分析该定理在证明不等式的思路和步骤方法。

第一步，要观察不等式的结构，思考假如将其进行变形后是否可以变为该定理的基本公式相关的形式。

第二步，在可以进行第一步变形的基本要求和前提下，应该分析题目给出的已知条件来构造出函数f(x)。

第三步，对所构造出的函数f(x)，要验证其是不是能够满足该定理的条件。

第四步，借助于f'(x)可以满足的不等式的条件求出要题目中需要证明的不等式。

下面，结合几个例题来详细讲解拉格朗日中值定理在不等式中的应用。

证明：设f(x)=arctanx，则可以在区间[0,h]上采用该定理进行运算，也即得：

讨论：对待本题，假如对该定理在不等式中的运用有比较清楚的认识，一般学习者解题都会构造函数，利用单调性等性质进行求解，然而，这样的解题是十分麻烦，而且计算量也很大，而利用该中值定理进行解题，问题则会简单得很多。同时也应该注意，由于拉格朗日中值定理中有求导的式子，所以要对arctanx、arccotx等一系列简单的求导公式要熟记于心，这是解题的基础，也是正确解题不可忽视的一部分。

2.2 拉格朗日中值定理在极限求解中的应用

该定理的应用十分广泛，在极限求解问题中也是经常使用到。大体来说，我们采用极限的定义、性质或者采用洛必达法则等一些常规方法来求极限，但是很多题目采用此定理来解答会方便快捷得很多，下面采用一些实例来说明在一些极限求解问题上运用此定理的好处。

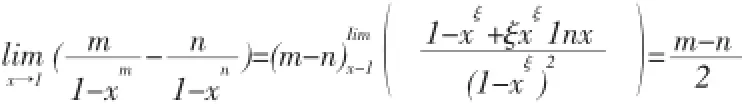
讨论：初看此题，似乎没有可以解题的方法和思路，但是注意到此题中和有一个共同的特点，也就是它们的结构是相同的，都可以表示为，这样采用该定理来求解，就会显得简单便捷的很多。

讨论：本题假如用极限的定义或者性质求解，将会很麻烦而且计算过程也会很复杂。假如仔细观察这类题目的特点，可以发现被减数和减数之间的自变量就相差为1，而这类题型的求解假如采用拉格朗日中值定理来求解，如上述解题过程，不仅方便，而且解题思路很清晰。

2.3 拉格朗日中值定理在收敛级数中的应用

该定理的也在判定级数的收敛性上有着具体的应用，最典型的例子是对调和级数的收敛性进行判断。下面通过这个例子的讲解，来分析此定理在收敛级数中的运用。

证明：假设f(x)=lnx，则f(x)在区间[N,N+1]上是连续的，在开区间（N，N+1）上可导，根据该定理可知，在区间（N，N+1）上至少存在着一点ξ，可以使得：

于是可得，当N=1时候，ln2-ln1〈1；当N=2时，有，当N=3时，有以此类推，可知，当N=n时，有

讨论：对调和级数的发散性，高等数学中只是指出用其发散性和其他级数相比较来判断其他级数的敛散性，对于调和级数的发散性的证明，假如仅仅使用级数的收敛性质或者判定准则进行判断是一件十分困难的事情，而本题中借助于该定理来判断调和级数的发散性，其解答过程简单，而且比较容易理解，不失为该定理在审敛级数中具体运用的典范。

3.结束语

拉格朗日中值定理作为微积分学中一个重要的核心定理之一，对于初学者来说，应当牢固对其基本概念以及有关该定理的应用进行系统学习。在借助于拉格朗日中值定理来解决不等式问题、极限求解问题以及判断级数的收敛性问题等一系列问题的核心是必须构造出满足该定理的辅助函数和相应的区间，然后才能对其采用拉格朗日中值定理来求解题目中的问题就显得很方便。所以，这里又要求我们对构造函数的性质、有关特征等一系列问题都必须搞清楚和真正弄懂弄通，对这些函数的使用范围要很熟悉。当然，除此之外，要加强数学能力的提高，而数学能力的提供的途径在于对问题多思考和加以总结和分析，并结合一定的习题练习，这样才能够更快更好的构造出拉格朗日中值定理的辅助函数来求解。

［1］华东师范大学数学系.数学分析(上册)[M].北京:高等教育出版社，2001.

［2］刘振航.关于拉格朗日中值定理的证明[J].天津商学院学报，2002,(5):35-36.

G642.3

A

2095-7327（2015）-08-0031-02

严海霞（1979.11—），女，江苏射阳人，硕士，讲师，就职于阜宁高等师范学校，研究方向为数学教学。