基于加权Voronoi图的无人飞行器航迹规划
2015-12-28聂俊岚张庆杰王艳芬
聂俊岚,张庆杰,王艳芬
(1.燕山大学 信息科学与工程学院,河北 秦皇岛066004;2.燕山大学 河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛066004)
0 引言
无人飞行器航迹规划问题可定义为:在给定的规划空间内,寻找飞行器从起始点到目标点的满足某种性能指标的最优航迹[1]。航迹规划的任务就是让飞行器以较小的威胁穿越阵地,最终到达目的地[2]。近年来,国内外研究人员已经对飞行器的航迹规划问题作了大量研究。目前用于航迹规划的算法大致可分为两类[3]:(1)确定型搜索算法,主要包括动态规划法、Voronoi图法、A*算法以及D*算法等;(2)随机型搜索算法,主要包括神经网络算法、遗传算法、粒子群算法、蚁群算法和模拟退火算法等。其中Voronoi图法与其他方法相比具有较强的直观性和把复杂的空域问题转换为区域划分问题的能力,有较好的时间特性和空间特性,适合单飞行器的航迹规划[4],且 Voronoi图法的航迹规划结果具有固有的威胁回避能力[5]。对于确定的威胁区域,Voronoi图边到周围威胁区域的距离是最远的;因此相比其他航迹规划方法,Voronoi图法能够计算得到更为安全的航迹。
目前,Voronoi图法在无人飞行器航迹规划领域已有较多进展。文献[5]将威胁源处理成平面点集,在规划空间内威胁分布一致的情况下,采用Voronoi图法进行飞行航迹的规划,并对航迹进行平滑和修正,其缺点是只将威胁源处理成平面点而没有考虑威胁源的覆盖范围,在实际应用中有较大局限性。考虑到威胁源的覆盖范围问题,文献[6]以雷达位置作为圆心,以雷达探测半径作圆,将雷达探测范围拟合成圆形区域,但其只考虑了一种扫描类型的雷达,而在实际的飞行空间中,不同威胁源有不同的作用方式和距离,只有研究具有不同作用方式和距离的威胁源的航迹规划才更有实际意义[7]。
此外,文献[6]也未考虑山峰等地形障碍,这些威胁源形状各异,如何对其进行拟合是无法回避的问题。文献[8]虽然考虑了地形等威胁因素,但其简单将海上岛屿拟合成椭圆形,造成了威胁源覆盖范围扩大的问题,进而可能会影响到最优航迹的计算。
针对上述问题,本文主要研究了在面对不规则地形以及类型各异的雷达威胁时,无人飞行器的航迹规划问题。首先对规划空间中的威胁区域进行预处理,采用文献[9-10]中提出的方法计算威胁区域的加权Voronoi图,在考虑飞行代价的基础上对计算得到的航迹进行平滑处理,最终规划出满足各项约束的最优航迹。
1 飞行空间预处理
实际情况中,山峰、雷达等威胁源都是三维的,为简化运算,本文将三维的雷达侦察区域和山峰等障碍物映射到二维空间进行处理。首先将威胁源处理成威胁区域,这些威胁区域的形状轮廓都不太规则,对其进行拟合时考虑两种解决方案:(1)轮廓外接圆法。如图1(a)所示,首先提取其轮廓,然后用轮廓的外接圆拟合该威胁区域,如图1(b)所示,显然这种方案会造成威胁区域的扩大;(2)轮廓均分法。提取出轮廓后,用若干半径相等的相交圆对威胁区域进行拟合,如图1(c)所示,这种办法依据山峰的轮廓绘制威胁区域,尽管计算量相比第一种方案要大,但其拟合出的威胁区域相比第一种方案要精确很多。本文采取将两种方案相结合的思路,对于轮廓形状近似于圆形的威胁区域用轮廓外接圆法对其进行拟合,而对于轮廓形状较为复杂的威胁区域,则用轮廓均分法进行拟合。
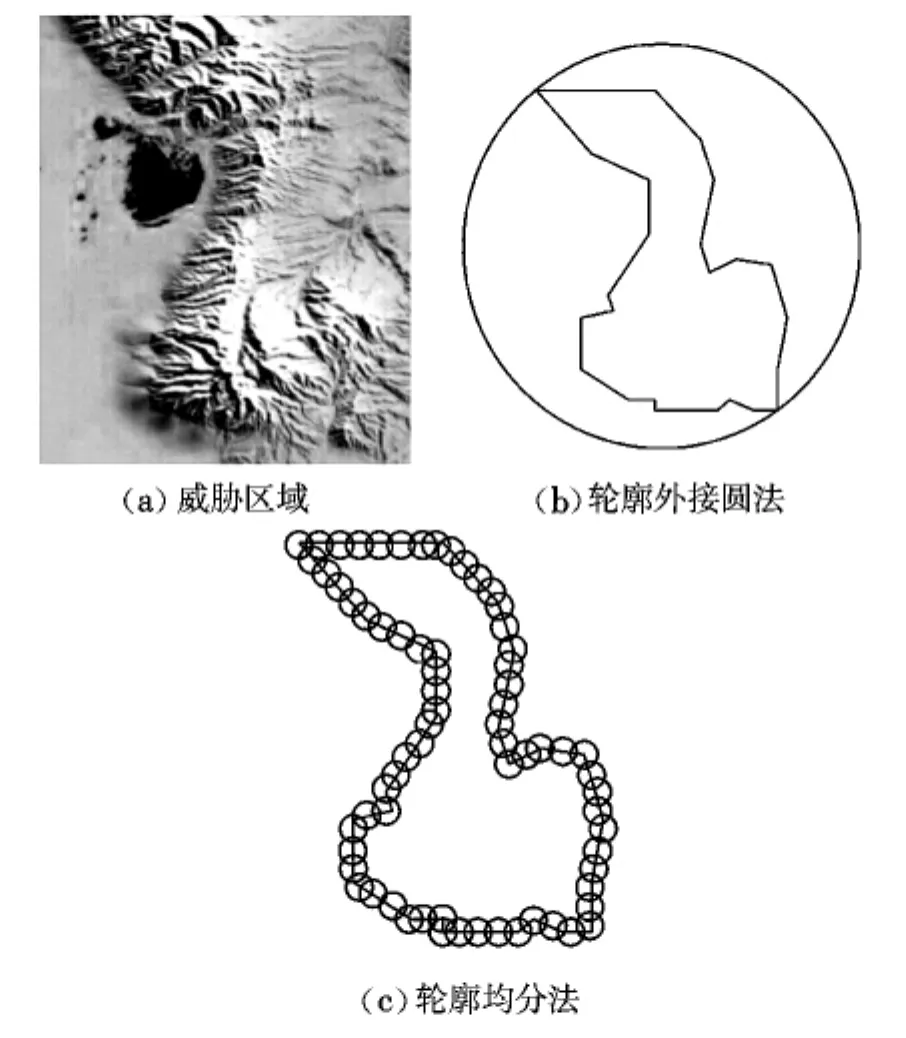
图1 威胁区域轮廓的拟合Fig.1 Fitting of threatening area’s outline
1.1 轮廓外接圆法拟合威胁区域
对图1(a)中的威胁区域进行外接圆的拟合。确定一个圆需要有圆心坐标(x0,y0)、半径(或直径)两个参数,设 S{(xi,yi)|i=1,…,n}为威胁区域轮廓上的n个点所构成的集合。用圆对威胁区域进行拟合的过程就是寻找外接圆的过程。其步骤为:
(1)计算边界点集S中任意两点间的距离dij(i,j=1,…,n;i≠j);
(2)寻找 dij中的最大值 max dij,记为 d,在 S中与d对应的两个点记为A(x1,y1)和B(x2,y2);
(3)求出线段AB的中点O(x0,y0),点O即为所需圆的圆心,线段AB为圆的直径。
1.2 轮廓均分法拟合威胁区域
对图1(a)中的威胁区域进行相交圆的拟合。同样设S{(xi,yi)|i=1,…,n}为待拟合威胁区域上的n个点所构成的集合,设一个偏离阈值p,最大圆半径Rmax,其步骤为:
(1)对威胁区域的轮廓进行直线拟合:
①从S中取一定数量连续点作为S的子集Si;
②用最小二乘法对Si中的点进行直线拟合,并计算每个点到直线的距离d;
③如果d>p,则从Si中去除一些连续点,再执行步骤②,直到满足需求,得到一条线段l;
④ 从S中去除Si,即执行S-Si;
⑤重复步骤①~④,直到S为空,最终得到拟合后的线段集合L{li|i=1,…,m}。
(2)取一条线段 li,若 li的长度 di>2Rmax,则令圆半径 R=Rmax,若 di≤2Rmax,则令 R=3di/4;
(3)从li的一个端点开始,每隔5/3R的长度取采样点,直到到达另一个端点,得到采样点集P{pi|i=1,…,n};
(4)以P中每个点为圆心,R为半径作圆。
通过以上工作,即可将不规则的轮廓用一系列相交的圆来覆盖。
2 航迹代价模型
航迹代价是衡量飞行器受到地形威胁或被雷达发现的可能性的指标。在现有文献中无人飞行器的代价函数通常包含长度代价和威胁代价[11]。考虑到飞行器转弯时物理性能的制约,文献[8]将最大转弯角引入到代价函数中。为提高飞行器完成任务的成功率,本文为飞行器加入警戒半径Rm,仅当航迹上任意一点到威胁区域的距离大于Rm时该航迹才可飞,因此为代价函数引入警戒半径参数θ,将航迹中两个转弯点之间的航迹称为一个“航迹段”,θ由航迹到威胁区域的距离s和Rm共同决定:若s>Rm,则θ=1,表示θ对于该航迹段的代价没有影响;若s≤Rm,则θ→∞,使航迹段代价为无穷大。对于某一航迹段Xi而言,其代价J为:

式中:J1,J2,J3分别为该航迹段的长度代价、威胁代价和转弯代价;w1,w2,w3为相应的权值。
对于某一航迹段Xi,若θ(Xi)→∞,则该航迹段的代价为∞;若θ(Xi)=1,则应计算其长度代价、威胁代价和转弯代价的加权和。长度代价与Xi的长度Li成正比,即J1(Xi)=Li。威胁代价指该航迹段上某个位置到周围威胁区域的距离,距离越近其威胁代价越大。转弯代价的计算模型和具体计算方式参见文献[11]。下面重点介绍威胁代价的计算方法,对于某一航迹段Xi,设一个实数K>1,其威胁代价计算方法为:
(1)以一定的步长对Xi进行采样,假设总共有n个采样点,则得到采样点序列P{1,…,n};
(2)设点Pj(j=1,…,n)距周围威胁区域的最短距离为sj,威胁代价为Tj,则有:
① 如果sj≥KRm,则 Tj=0;
② 如果 Rm≤sj<KRm,Tj=1 -sj/(KRm);
(3)Xi的威胁代价J2(Xi)即为Xi航迹段所有采样点的威胁代价之和:
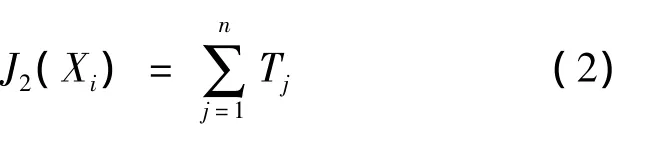
3 基于加权Voronoi图的航迹规划
3.1 算法分析
首先,对于近似圆形的威胁区域用“轮廓外接圆法”直接进行拟合。而对不规则区域进行拟合时,为了使参与计算的几何图形一致从而减少计算的复杂性,本文采用“轮廓均分法”进行拟合,得到一系列相交的圆形区域,相交圆之间生成的加权Voronoi图边会与这两个圆相交,因此通过判断某一条边是否与圆相交来决定是否摒弃这条边。
其次,加权Voronoi图边到其周围圆的距离都相等,如图2所示,在边上任取A,B两点,其到周围两个圆的距离都相等,生成的飞行航迹处于距离威胁区域尽可能远的位置,使危险性降到相对最低。
生成加权Voronoi图后,加权Voronoi图边的交点即为飞行器的可飞节点,所有可飞节点构成了飞行器的可飞节点集,可飞节点集与加权Voronoi边共同构成了一个网络,可用赋权图来描述它[12],对于这个可飞航迹构成的赋权图,可以用Dijkstra算法寻找一条最短航迹。
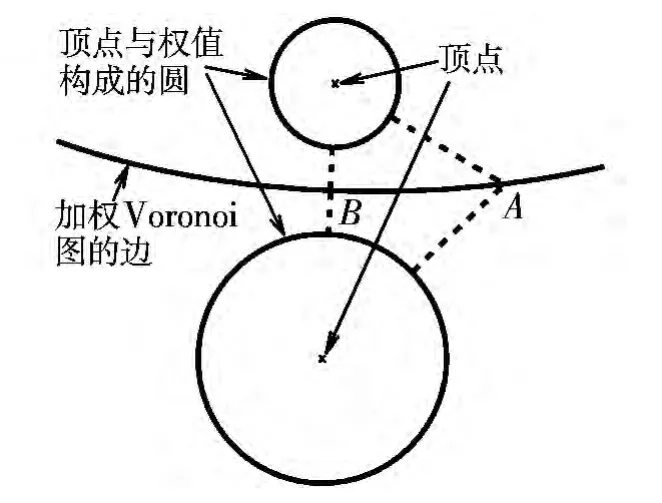
图2 加权Voronoi图Fig.2 Weighted-Voronoi diagram
3.2 算法步骤
(1)采用轮廓外接圆和轮廓均分相结合的方法对飞行空间内的威胁区域进行预处理,得到一系列圆形区域,并读入起始点和目标点;
(2)计算所有圆的加权Voronoi图,图的所有边构成了航迹段集合X{Xi|i=1,…,n}。加权Voronoi图的边大多为曲线段(在计算机中曲线段由若干直线段组成,因此每条曲线段上都有若干折点),每条边都是一条航迹段,边的交点即为拐弯点;
(3)设飞行器的警戒半径为Rm,对于某一航迹段Xi,若Xi的飞行代价为无穷大,则Xi为不安全航迹段,将其从集合X中剔除;
(4)从图上寻找距离飞行器的起始点和目标点最近的两个拐弯点,用Dijkstra算法求取这两个拐弯点之间的最短航迹W;
(5)以航迹W上的每个拐弯点以及每个航迹段的折点作为控制点,用2次B样条函数对航迹进行平滑,得到平滑的航迹W';
(6)输出平滑后的最短航迹W'。
4 仿真试验及分析
4.1 仿真试验
本文使用的飞行空间为600 km×600 km,如图3所示。其中,a为飞行器起始点(70 km,50 km),b为目标点(430 km,420 km),虚线区域为雷达侦察区域。采用“轮廓均分法”对大型山脉的轮廓进行拟合,对小型的山峰和雷达威胁用“轮廓外接圆法”拟合。
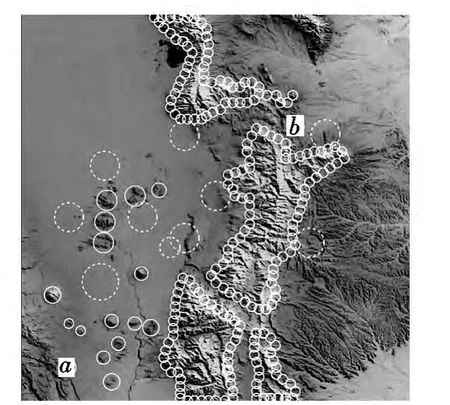
图3 飞行空间示意图Fig.3 Flying space
当警戒半径Rm=5 km时,经本文算法处理,得到加权Voronoi图如图4所示,黑色细线为加权Voronoi图的边,即航迹段,较宽的曲线为平滑后的最短航迹,该航迹是由一系列采样点组成。每个采样点的灰度值是根据该点的威胁代价从灰度条带上采集得到,颜色越深则威胁代价越大(见图5)。
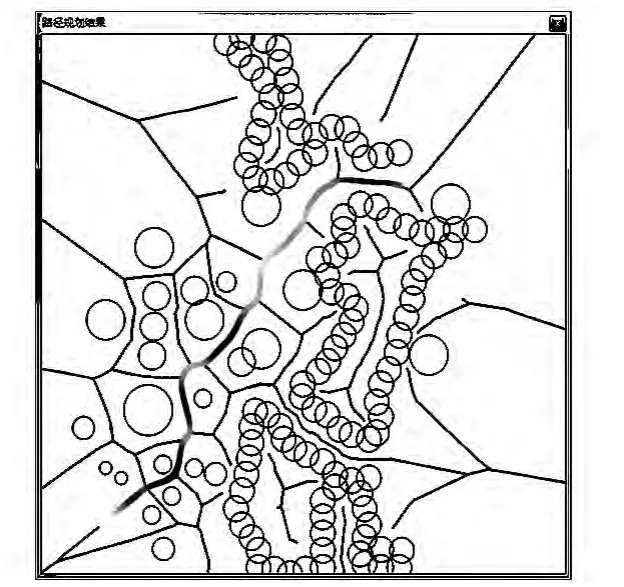
图4 加权Voronoi图及最短航迹Fig.4 Weighted-Voronoi diagram and shortest path

图5 灰度条带Fig.5 Gray image
在同样的飞行空间中仅用轮廓外接圆法对威胁区域进行拟合并生成航迹,当警戒半径Rm=5 km时,得到如图6所示的仿真结果。

图6 轮廓外接圆法生成的航迹Fig.6 Paths Generated by using circumcircle fitting method
表1为从对威胁区域拟合的不同方法和警戒半径大小两方面,考察不同因素对最终生成的航迹的影响。当Rm=8 km或Rm=11 km时,轮廓外接圆法已经无法得到符合条件的航迹,说明这种拟合方法会造成威胁区域范围扩大的问题,尽管计算时间较短,但其生成的航迹较长,且当警戒半径较大时容易出现“不可飞”的情况。采用轮廓均分和轮廓外接圆相结合的方法可以很好地解决这些问题,尽管计算时间较长,但其仍然能满足即时性需求。
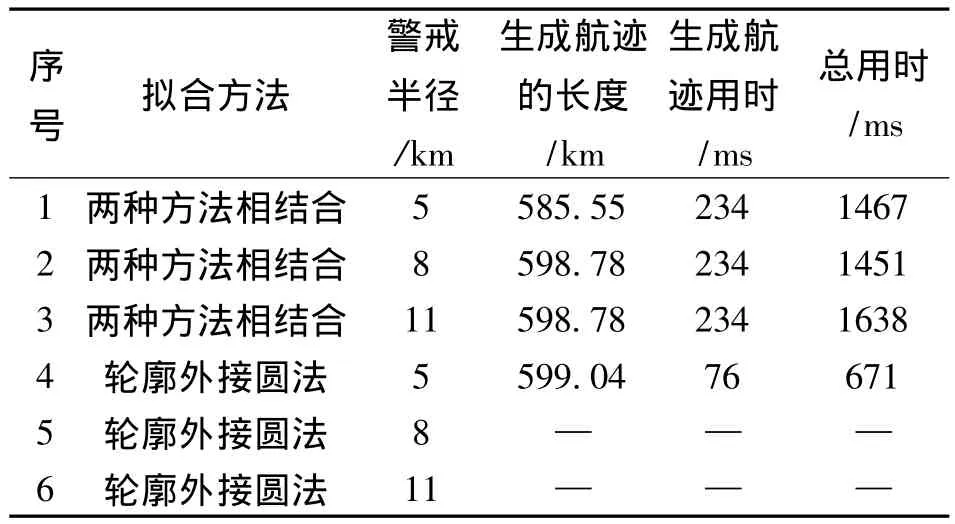
表1 航迹生成结果比较Table 1 Comparison of the paths
4.2 可视分析
为了使最终生成的航迹能够更好地支持决策,采用了多种可视化和交互式的手段来展示航迹规划结果,最终规划的航迹如图7(a)所示,通过航迹上不同位置的颜色深浅能直观地看出该位置的危险程度。
作为一个支持决策的工具,提供具体数据的可视化展示同样非常必要,图7(b)所示为图7(a)中的航迹上各个采样点到威胁区域的详细距离信息。与图7(a)中的航迹类似,图7(b)中的曲线也用不同灰度值的颜色表示距离的远近,即威胁的大小。
在图7(b)上可以进行一些交互式操作。用鼠标滚轮可以放大或缩小图表的大小,右键可以对图表进行拖拽操作,左键可以在图表上进行框选,选中一定区域后,实时地在航迹图上标识出对应的航迹段,如在图7(b)中用鼠标左键进行框选后,图7(a)中会圈出相应的航迹位置。
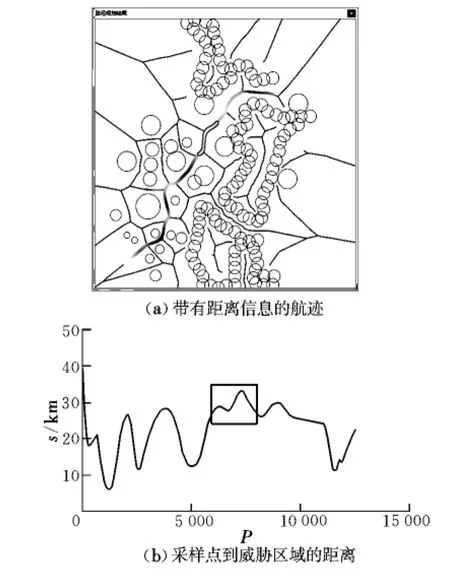
图7 可视分析Fig.7 Visualization analysis
5 结束语
本文主要研究了在二维空间采用加权Voronoi图对无人飞行器进行航迹规划的问题。相比传统Voronoi图法,加权Voronoi图可用于处理具有不同覆盖范围的威胁源的航迹规划,更具实际意义。此外,采取轮廓均分与轮廓外接圆相结合的方法拟合各种威胁区域的轮廓,有效地解决了传统拟合方法造成的威胁区域扩大问题。将警戒半径引入航迹代价模型,使最终生成的航迹更为安全。另外,程序还提供了可视分析功能,决策者可以从多角度分析生成的航迹。试验结果表明,本文方法能规划出更安全且长度较短的航迹,可视化方法的加入为决策者分析航迹提供了交互手段。为简化运算,本文将飞行空间简化到二维空间,而三维空间的航迹规划更具实际意义,因此三维空间内的航迹规划将会是今后的主要研究方向。
[1] 严平,丁明跃,周成平,等.飞行器多任务在线实时航迹规划[J].航空学报,2004,25(5):485-489.
[2] 刘振,史建国,高晓光.Voronoi图在航迹规划中的应用[J].航空学报,2008,29(S1):15-19.
[3] 王维平,刘娟.无人飞行器航迹规划方法综述[J].飞行力学,2010,28(2):6-10.
[4] 赵文婷,彭俊毅.基于VORONOI图的无人机航迹规划[J].系统仿真学报,2006,18(S2):159-162.
[5] 阎代维,谷良贤,王兴治.基于Voronoi图的巡航导弹突防路径规划研究[J].弹箭与制导学报,2005,25(2):11-13.
[6] 单提晓,蒋蓁.一种基于分割法的无人机路径规划新方法[J].弹箭与制导学报,2014,34(2):185-188.
[7] 马培蓓,纪军.3种多导弹航迹规划算法的比较[J].电光与控制,2010,17(10):28-32.
[8] 傅阳光,周成平,胡汉平.无人飞行器海上航迹规划差分进化算法研究[J].兵工学报,2012,33(3):295-300.
[9] Karavelas Menelaos I,Emiris Ioannis Z.Predicates for the planar additively weighted Voronoi diagram[R].ECGTR-122201-01,2002.
[10] Karavelas M I,Emiris I Z.Root comparison techniques applied to computing the additivelyweighted Voronoi diagram[R].ACM-SIAM SODA-15,2003.
[11]傅阳光,周成平,丁明跃.基于混合量子粒子群优化算法的三维航迹规划[J].宇航学报,2010,31(12):2657-2664.
[12]张同法,于雷,刘文杰,等.基于Dijkstra算法的巡航导弹航迹规划方法研究[J].弹箭与制导学报,2008,28(4):65-67.
