飞翼布局飞行器大迎角非定常气动建模

王可，刘超

(1.中国民航飞行学院 飞行技术学院，四川 广汉618307;2.南京航空航天大学 航空宇航学院，江苏 南京210016)

0 引言

评估飞翼布局的动态特性，特别是精确预测飞行器大迎角时的非定常气动力载荷变化趋势，对于战斗机大迎角过失速区域的气动特性的研究、分析和仿真以及飞控系统的设计极为重要。大迎角非定常气动特性研究主要通过数值方法或风洞试验进行系统辨识来获取精确的数学模型［1］。

传统的气动力模型是在稳定性导数方法的基础上，通过模型运动相关参数和气动载荷的线化关系来预估瞬时气动系数［2］。但在大迎角区域有强烈的非定常气动现象时，传统线性气动模型已经不能精确地描述整个系统的变化与发展。Tobak等［3］在1976年提出了具有严格表述的非线性指数响应方法，虽然可以降低方程的求解难度，但实际工程建模中数据处理和参数预估困难。另一种有效方法是通过微分方程进行描述。Goman等［4］提出状态空间模型，引入了具有明确物理意义的气动分量作为流场内部变量，考虑了内部流场的拓扑结构，使建模精度有所提高。文献［5-7］也证明了状态空间法表述非定常现象的可行性。

近年来，模糊逻辑［8-9］、神经网络［10］、最小二乘支持向量机等方法也被运用到非定常条件气动建模过程中。这些方法对样本值的质量要求较高，能够精确给出样本值范围内的预测结果，但模型的外插能力一般。

本文采用状态空间法模型，对常规飞翼布局无人飞行器的单独俯仰和单独滚转小振幅振荡建立非定常模型。利用动导数计算和参数预估得到特征时间常量，研究模型的非定常特性。通过对建模结果的分析和验证，论证状态空间模型的适用性。

1 试验模型和设备

试验模型构型采用北约RTO(Research and Technology Organization)组织的代号为SACCON的常规飞翼布局无人飞行器［11-12］，如图1所示。模型缩比率为0.26;材质为 ABS工程塑料;质量为0.625 kg;具有典型λ翼型平面;平均气动弦长c¯=0.2759 m;模型投影表面积S=0.0521 m2。模型机翼外翼段相对于前缘有5°上扭角，用来推迟大迎角范围内的翼面流动分离，以便在更大迎角范围内研究非定常气动特性。

图1 SACCON试验模型Fig.1 Model of the SACCON

试验在南京航空航天大学NH1低速低湍流开口回流式风洞中进行，试验出口段为1.5 m×1.0 m矩形开口，设计最高风速40 m/s。动态试验风速25 m/s，Re≈0.5 ×106。

2 气动导数分析及辨识

当飞行器在涡系破碎迎角区域内做振荡运动时，气动力将表现出强烈的迟滞特性，致使非定常气动导数显著依赖于振动幅度和频率，因此需要对传统的气动导数线化模型进行修正［13］。从小扰动理论出发，气动导数可以表示为(以法向力系数CN为例):式中:CN0为稳态法向力系数;CNα和为法向力系数随迎角和迎角变化率的导数;CNq和为法向力系数随俯仰角速度和角加速度的变化率;q为俯仰角速度。

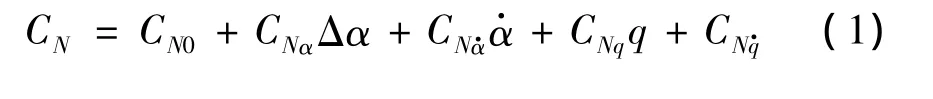
小振幅俯仰振荡时，迎角在中心迎角α0附近的变化规律为:

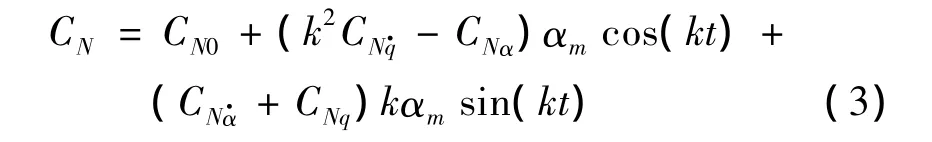
将气动力或力矩系数看作是时间的连续函数Ci(t)(i=X，N，Z，m，l，n)，且其变化规律和运动周期振荡一致，因此气动函数通过拓展可以看作是时域上的周期函数，且满足收敛条件(狄利克雷充分条件)。以法向力系数为例，CN(t)可以表示为如下形式:

式中:a0，a1，b1为傅里叶级数的系数。

比较式(2)和式(3)，通过傅里叶级数的系数公式求解动导数。图2、图3分别是振幅为5°时，单独俯仰和单独滚转的同相、反相动导数随角度变化的分布曲线图。图中，α0和β0为中心角度，不代表任意迎角和侧滑角。

由图2可以看出，在20°～40°迎角范围内，由于翼面涡破碎点的存在，动导数依赖频率的特性愈发明显，使气动导数具有强非线性和非定常特性。由图3可以看出，在小测滑角)范围内，气动系数显现出强烈的非定常特性。

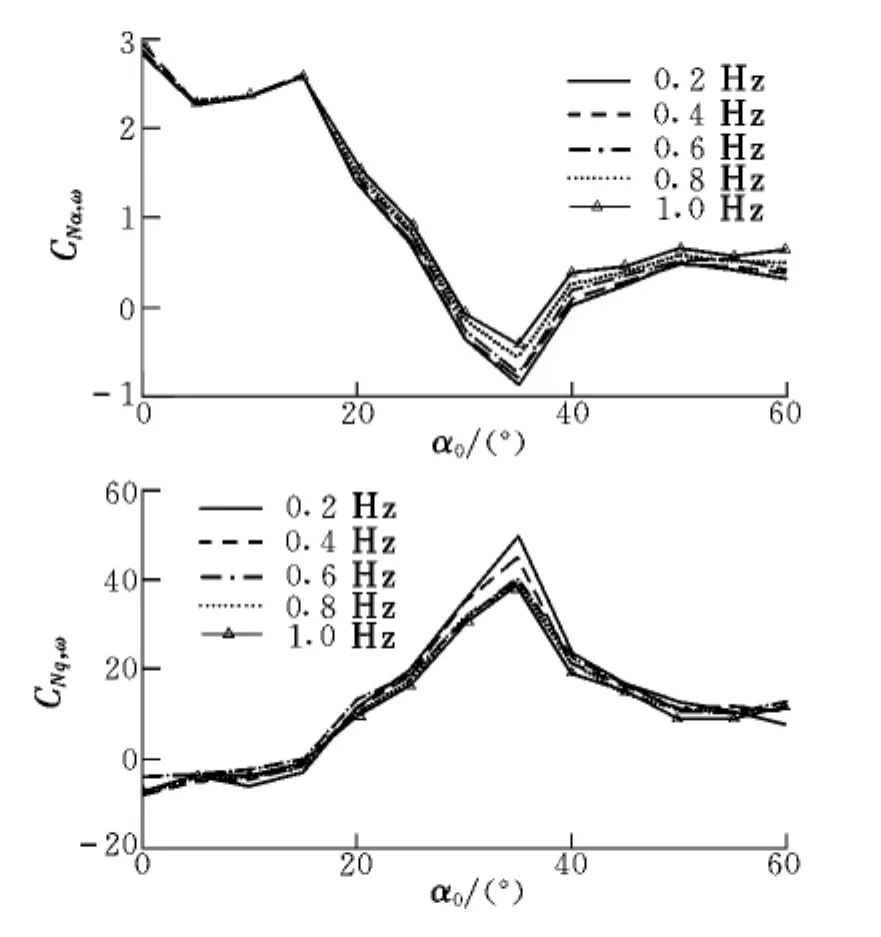
图2 CN的同相、反相导数随迎角的变化Fig.2 Variation of in-phase and out-of-phase components of CN with AOA

3 非定常气动力的数学模型及辨识方法

研究表明，飞行器在迎角变化过程中，表面流场的主要拓扑结构有层流结构、机头强对涡结构，以及沿机翼前缘延伸至翼尖的涡流结构和涡破碎结构。当飞行器在大迎角机动时，非定常流动现象主要与飞行器表面涡流的行程和破碎位置变化相关。当涡流的调整时间远远超过对流的调整时间时，气动力显现出迟滞效应。因此，可以将气动力系数表述为如下普遍形式:

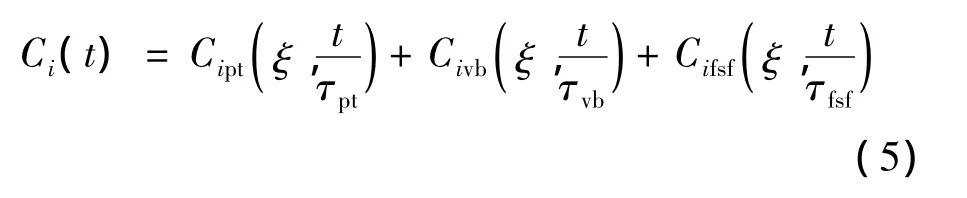
式中:i=(X，N，Z，m，l，n)为气动分量;ξ=(α，β，p，q，，…)为运动参数;τ为流态的内部调整特征时间常数;下标:pt代表势流;vb代表涡破碎流动;fsf代表完全失速流。CFD数值模拟计算结果表明，相比附着流和涡破碎流，完全失速流动的气动贡献很小，可以忽略。涡破碎流动项Civb可以用如下形式来表述其迟滞特性:

以SACCON模型小振幅单独俯仰运动的法向力系数CN为例来说明两步线性回归方法。基于状态空间法的线性模型可以表示为:

式中:q为滚转角速度;CNpt为假设气流无分离时的静态气动力系数;CNq，pt为俯仰运动时旋转流场导致的附加定常气动导数;CNvb为运动过程中由于流场涡系拓扑结构迟滞产生的非定常气动力系数;ΔCN=CNst－ CNpt，CNst为静态法向力系数。

根据式(2)中的角度变化关系，将式(8)线性化，得到:

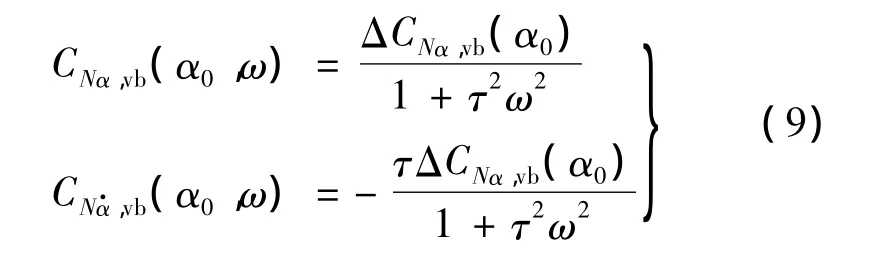
加上势流项，总的气动导数可以表示为:

根据计算得到的同相和反相动导数，从式(10)可以推导出预估特征时间常数τ的公式:

采用常规最小二乘法［15］进行第一步线性回归，由回归结果可以得到τ，将其代入式(10)中，进行第二步线性回归，辨识得到 CNα，pt，CNq，pt，ΔCNα，vb。至此，式(9)中的所有参数均辨识出来。

对于大振幅振荡运动，为了得到更高精度的建模结果，可以将式(8)变为如下的非线性形式:

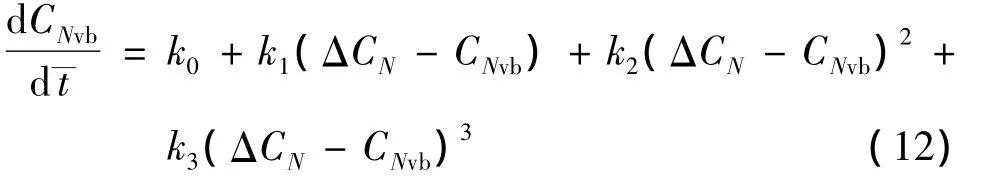
非线性模型中，特征时间常数τ=1/k1。

4 状态空间模型结果与分析

图4给出了小振幅单独俯仰振荡运动时，不同频率(0.2 Hz，0.4 Hz，0.8 Hz，1.0 Hz)下的同相和反相导数分布关系和该运动状态下的带有误差限的特征时间常数τ的分布，可以看出，在20°～30°迎角范围内，同相和反相导数近似地落在一条直线上，表明了气动导数项与振荡频率的依赖性。

图4还给出了第二步线性回归的辨识结果。图中:CN，sta为试验测量的静态法向力系数;CN，exp为试验得到的中心迎角30°、振幅15°、频率0.6 Hz时的动态法向力系数;CN，att为模型辨识得到的势流贡献的气动分量;CN，dyn为通过模型辨识得到的动态涡破碎引起的气动分量;ΔCN，vb为大振幅运动过程辨识得到的涡破碎迟滞变化量;CN，mod1为由线性模型辨识得到的总的法向力气动系数结果;CN，mod2为由非线性模型辨识得到的总的法向力气动系数结果。

同样，对于固定迎角α=30°的小振幅单独滚转运动，得到的结果如图5所示。

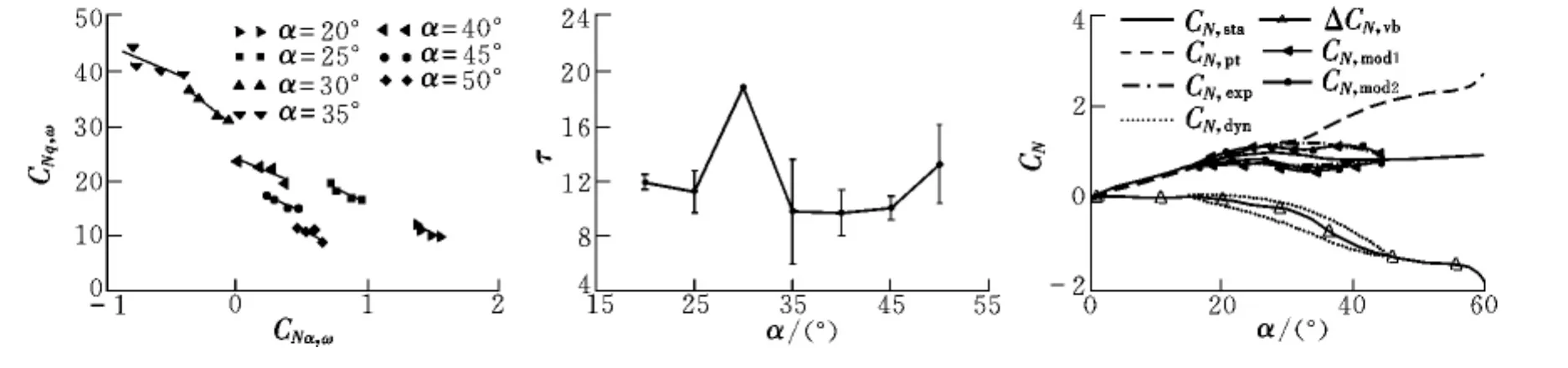
图4 法向力系数的参数辨识及纵向状态建模结果与试验数据比较Fig.4 Identification results for pitch oscillation and comparison for longitude

图5 滚转力矩系数的参数辨识及横航向状态建模结果与试验数据比较Fig.5 Identification results for roll oscillation and comparison for lateral conditions

通过纵向运用状态空间法的线性和非线性建模结果和试验结果对比，可以清楚地看到二者基本一致。说明状态空间模型可以在一定程度上描述飞翼布局飞行器在大迎角下的非线性和非定常特性。同时，状态空间线性模型和非线性模型的结果对比并不非常明显，表明纵向线性模型也可以达到非线性模型的建模精度。而横航向的建模结果与试验数据对比变化趋势一致，但是存在一些误差，可能由于翼面上展向涡系影响了状态空间模型的表达方式。

5 结束语

建模预测结果和试验数据的对比表明，建立的数学模型可以在一定程度上描述SACCON飞行器的非定常气动特性，特别是纵向建模结果具有较高的建模精度。但横航向建模与试验数据的误差表明，还需要更深入了解该构型下的流场结构，以应对具有更复杂外形的飞行器。

［1］ Murphy PC，Klein Vladislav.Estimation of unsteady aerodynamic models from dynamic wind tunnel data［R］.RTO-MP-AVT-189，2011.

［2］ Bryan G H.Stability in aviation［M］.London:Macmillan and Company，1911.

［3］ Tobak M，Schiff L B.On the formulation of the aerodynamic characteristics in aircraft dynamics［R］.NASA TRR-456，1976.

［4］ Goman M，Khrabrov A.State-space representation of aerodynamic characteristics of an aircraft at high angles of attack［J］.Journal of Aircraft，1994，31(5):1109-1115.

［5］ Abramov N B，Goman M G，Greenwell D I，et al.Two-step linear regression method for identification of high incidence unsteady aerodynamic model［R］.AIAA-2001-4080，2001.

［6］ 汪清，蔡金狮.飞机大攻角非定常气动力建模与辨识［J］.航空学报，1996，17(4):391-398.

［7］ 史志伟，倪芳原，陈永亮.基于两步线性回归的状态空间模型建立与验证［J］.空气动力学学报，2013，31(6):699-703.

［8］ 史志伟，明晓.基于模糊聚类的模糊神经网络在非定常气动力建模中的应用［J］.空气动力学学报，2005，23(1):21-24.

［9］ Wang Zhongjun，Edward L C，Brandon J M.Fuzzy logic modeling of nonlinear unsteady aerodynamics［R］.AIAA-98-4351，1998.

［10］史志伟，王峥华，李俊成.径向基神经网络在非线性非定常气动力建模中的应用研究［J］.空气动力学学报，2012，30(1):108-112.

［11］ Cummings R M，Schütte Andreas.An integrated computational/experimental approach to UCAV stability＆control estimation［R］.AIAA-2010-4392，2010.

［12］ Loeser T D，Vicroy D D，Schütte Andreas.SACCON static wind tunnel tests at DNW-NWB and 14'×12'NASA LaRC［R］.AIAA-2010-4393，2010.

［13］ Greenwell D I.Difficulties in the application of statility derivatives to the manoeuvring aerodynamics of combat aircraft［C］//The International Council of the Aeronautical Sciences(ICAS)and the American Institute of Aeronautics and Astronautics，Inc.，1998.

［14］ Klein Vladislav，Murphy Patrick C，Szyba N M.Analysis of wind tunnel lateral oscillatory data of the F-16XL aircraft［R］.NASA/TM-2004-213246，2004.

［15］ Klein Vladislav，Morelli E A.Aircraft system identification theory:theory and practice［M］.USA:American Institute of Aeronautics and Astronautics，2006.