飞机中性速度稳定性PIλDμ控制律设计

王海涛，董新民，周倩，程建锋，王哲

(1.空军工程大学 航空航天工程学院，陕西 西安710038;2.中航工业南京机电液压工程研究中心，江苏 南京211100;3.空军西安飞行学院 理论训练系，陕西 西安710300)

0 引言

现代高性能战斗机电传控制系统的控制律设计中，中性速度稳定性控制律［1］已成为标准化配置。采用中性速度稳定性控制律的主要目的是为了解决用杆力作为输入信号时，输入到比例式控制增稳操纵系统中对驾驶员造成的配平困难。其核心优点是可实现飞机自动配平，从而大大简化飞行员操纵程序、降低劳动强度，如单独推油门实现平飞加速和松杆稳定飞行等。最常见的实现形式是在杆力指令与过载反馈信号综合处的下游插入“比例+积分”环节［1］，即整数阶PI控制器。然而，传统PID控制器存在控制效果差、对飞行状态过于敏感、参数整定工作繁重等缺陷，限制了控制性能的提高;另外中性速度稳定性没有明确的标准要求，PI控制器通常只作为控制增稳控制律的一个动态环节，其参数根据控制增稳性能准则确定后仅针对外部扰动和自动配平性能进行有限的验证与改进。这些都大大限制了中性速度稳定性的性能。

分数阶微积分与整数阶微积分几乎同时起源，它将微积分阶次推广到任意实数甚至复数，因其计算复杂且无明确物理意义，长期局限于数学理论研究，而未得到广泛应用［2］。数学基础理论和计算机技术的发展，为分数阶控制器的设计应用提供了可能，其中 Podlubny［3］提出的 PIλDμ控制器是分数阶控制应用的一个里程碑。考虑到大气粘性、压缩性等也具有分数阶微积分性质，因而文献［4-6］已将分数阶控制理论引入飞行控制，并已取得一定成效。

考虑到分数阶PIλDμ控制器更多的控制自由度和更精确的频域调整能力，本文将设计PIλ控制器，对传统PI控制器实现中性速度稳定性的不足加以改进。

1 分数阶微积分定义

分数阶微积分的定义方法很多，本文介绍两种适用于控制应用的定义方法［7］。

(1)Caputo定义为:

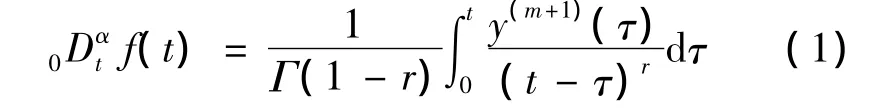
式中:α =m+r，m 为整数，0 ＜ r≤1;Γ(z)为伽马函数，是阶乘n!的推广。对式(1)进行拉氏变换得:

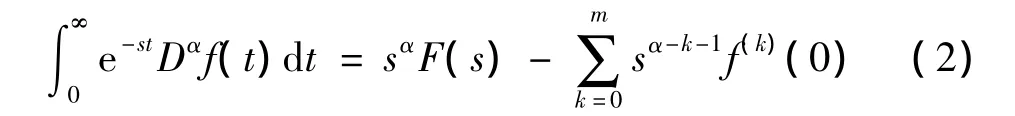
若f(k)(0)=0，则式(2)中的和式部分可以忽略。Caputo定义使Laplace变换更为简洁，便于分数阶微分方程的求解。

由定义(1)可知，连续函数在某点上的分数阶微分不是求该点处的极限，而是与从初始时刻到该点的所有时刻的函数值有关，因此分数阶微积分具有较强的记忆性，这是分数阶微积分异于整数阶微积分的最大优点。

(2)Grunwald-Letnikov(G-L)定义为:

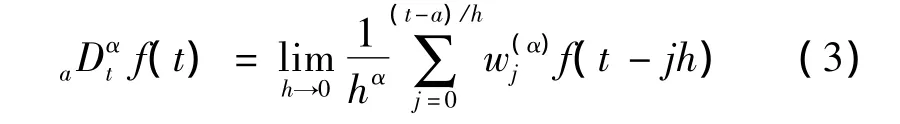
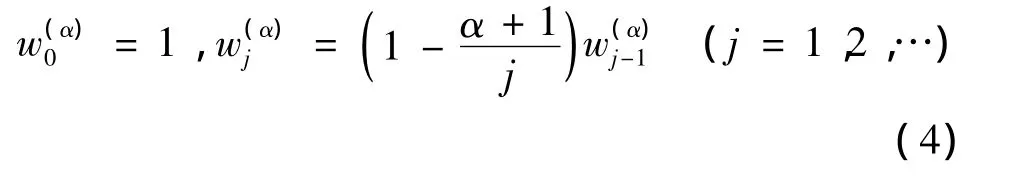
依此定义可推导出分数阶微分近似计算公式:

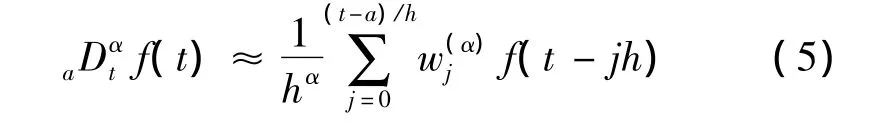
当步长h足够小时，式(5)即可较为准确地近似函数的分数阶微积分。G-L定义可直接用于分数阶微积分的离散化和数值计算。

2 分数阶PIλDμ控制器原理与实现

2.1 分数阶PIλDμ与整数阶PID的关系

由Caputo定义可知，零初始条件下的分数阶PIλDμ控制器［2］传递函数可表示为:

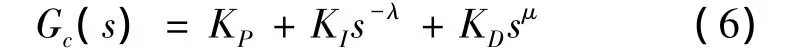
式中:λ，μ＞0为任意实数。与整数阶PID控制器相比，分数阶PIλDμ控制器的积分与微分项阶次可变，即将整数阶PID控制器推广为无限维“空间”，二者之间的关系如图1［7］所示。

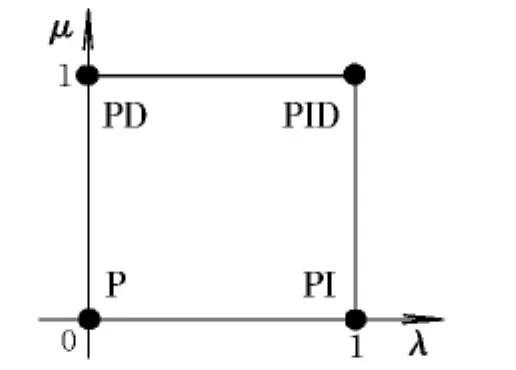
图1 PIλDμ阶次取值平面Fig.1 Plane of the order value of PIλDμ

由图可知，分数阶PIλDμ取值空间为整个平面，而整数阶PID只是其特例。由于取值空间的大大扩展，使分数阶PIλDμ调节自由度更多，为获得更佳的控制效能带来了可能性［2］。

从频域特性来看，整数阶PID只能使系统的幅频曲线斜率以20 dB/dec(分贝/十倍频程)的整数倍变化，而分数阶Laplace算子sr的幅频曲线斜率为20r dB/dec(r为任意实数)，因此分数阶PIλDμ对系统幅相特性的调整更加灵活精细。

2.2 分数阶微积分算子sr的频域近似拟合

目前现有计算工具无法直接进行分数阶运算，因此用整数阶系统近似拟合分数阶系统成为折中的研究思路。方法之一是利用G-L定义，直接进行离散化，该方法适用于数值仿真，但迭代计算量与拟合精度的矛盾往往难以调和。因此本文以Caputo定义为出发点，对Oustaloup频域拟合算法［7］进行研究与改进。

Oustaloup算法［8］的实质是用一组串联的整数阶滤波器在选定的频段内对分数阶Laplace算子sr进行近似拟合，其对任意时间函数f(t)的分数阶微积分相当于f(t)经该组滤波器后的输出0Dαtf(t)，算法原理如图2所示。

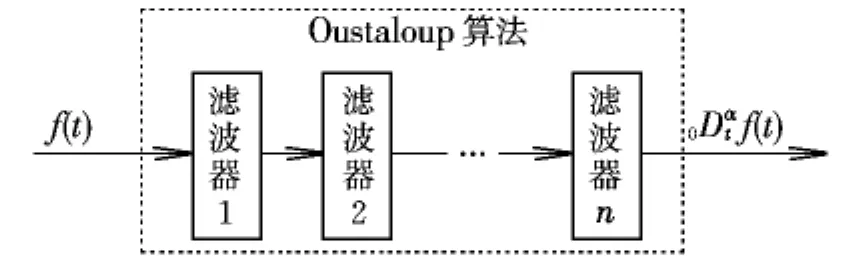
图2 Oustaloup算法功能示意图Fig.2 Function of the Oustaloup algorithm

Oustaloup算法对分数阶Laplace算子sr的频域近似拟合原理如图3［8］所示。

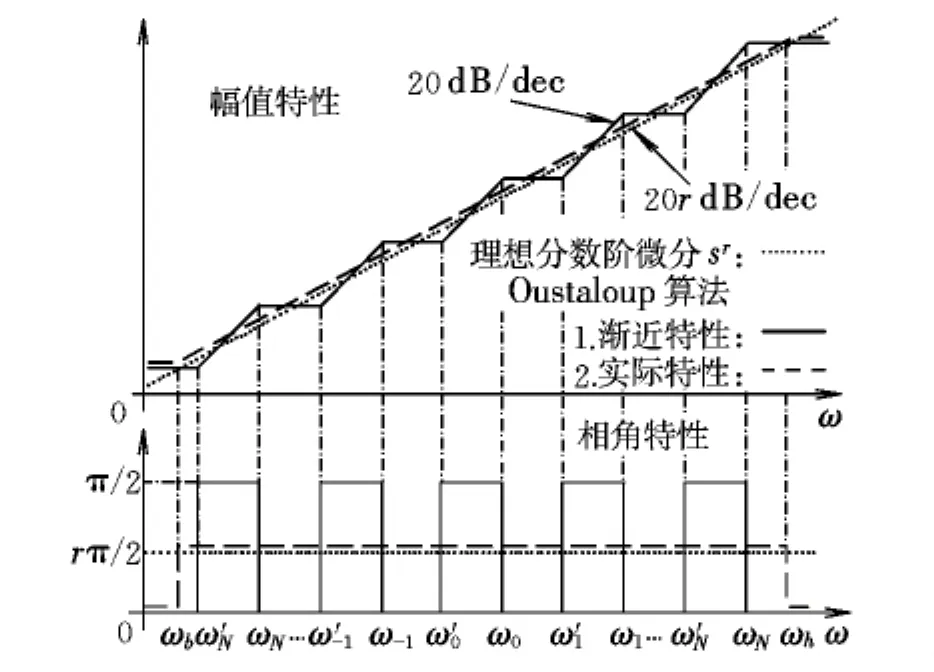
图3 Oustaloup算法的近似拟合原理Fig.3 Principle of the approximate fitting function of the Oustaloup algorithm

由图3可知，Oustaloup算法的基本思路是合理选取各级滤波器的交接频率ω'i和ωi，以使整体滤波器的频域特性近似拟合理想分数阶Laplace算子sr。因而假定选定的拟合频率段为(ωb，ωh)，则Oustaloup算法的整数阶多级滤波器传递函数模型可表示为:

其中ωbωh=1，经推导得各级滤波器交接频率和增益值为:

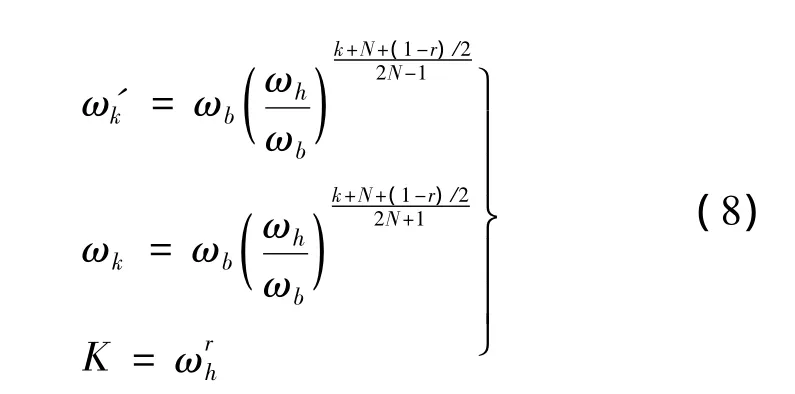
式中:r为拟合分数阶Laplace算子sr的阶次;N为滤波器级数。这种多级滤波器串联结构，对扰动具有很强的抑制作用。通常，N≥5时即可保证较好的拟合效果，综合复杂度考虑，本文选取N=5。

2.3 分数阶微分算子sr的仿真实现

本文在Simulink环境下，对上述算法进行仿真，实现了任意频段的精确拟合，并从时域输出响应和频域特性两个方面，将所设计的分数阶Laplace算子sr模块与Simulink的积分模块进行了仿真对比分析，其结果分别如图4和图5所示。

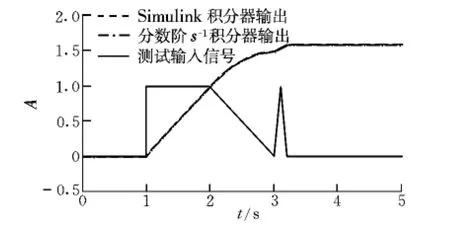
图4 Oustaloup微积分模块的时域输出特性Fig.4 Time field output characteristics of the Oustaloup calculus module

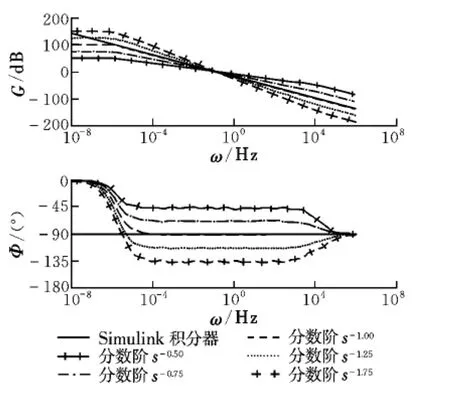
图5 Oustaloup微积分模块的频域输出特性Fig.5 Frequency field output characteristics of the Oustaloup calculus module

图4 与图5中，拟合频率段均为(ωb=10－5Hz，ωh=105Hz)。由此可知，本文设计的分数阶sr模块，当r=－1时积分效果与Simulink积分模块近乎完全相同;在选定的频域段内，频域特性与理想分数阶Laplace算子sr基本一致。即具有较好的时域和频域特性，进而可方便地实现PIλDμ控制器。

3 飞机中性速度稳定性PIλ控制器设计

本文将分数阶PIλ控制器替换传统PI控制器应用于飞机中性速度稳定性控制律的设计。为便于对比分析，本文采用文献［9］所述的F-16飞机及其电传控制律仿真模型为控制对象。假定初始状态为巡航，高度为3 000 m，空速为260 m/s。针对纵向小扰动飞机模型，引入分数阶PIλ控制器后，升降舵偏角δe的控制律为:

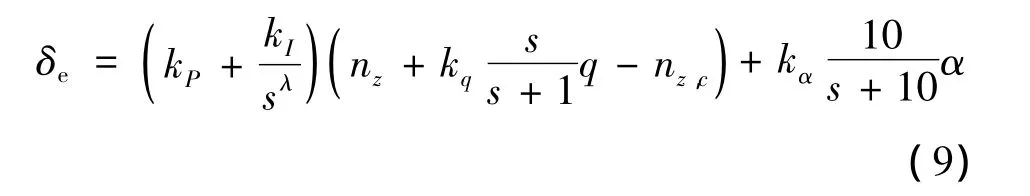
为对比分析PIλ控制器与PI控制器的优劣，使kq=0.334，kα=0.5，二者完全相同，仅根据控制增稳性能的要求对分数阶PIλ控制器进行调参，其结果为:

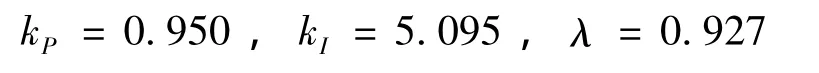
3.1 PIλ控制器的控制增稳性能

中性速度稳定性实现的前提是满足控制增稳性能要求。对于Δnz，c=1的法向过载指令，两种控制器下的飞机法向过载短周期响应过程如图6所示。

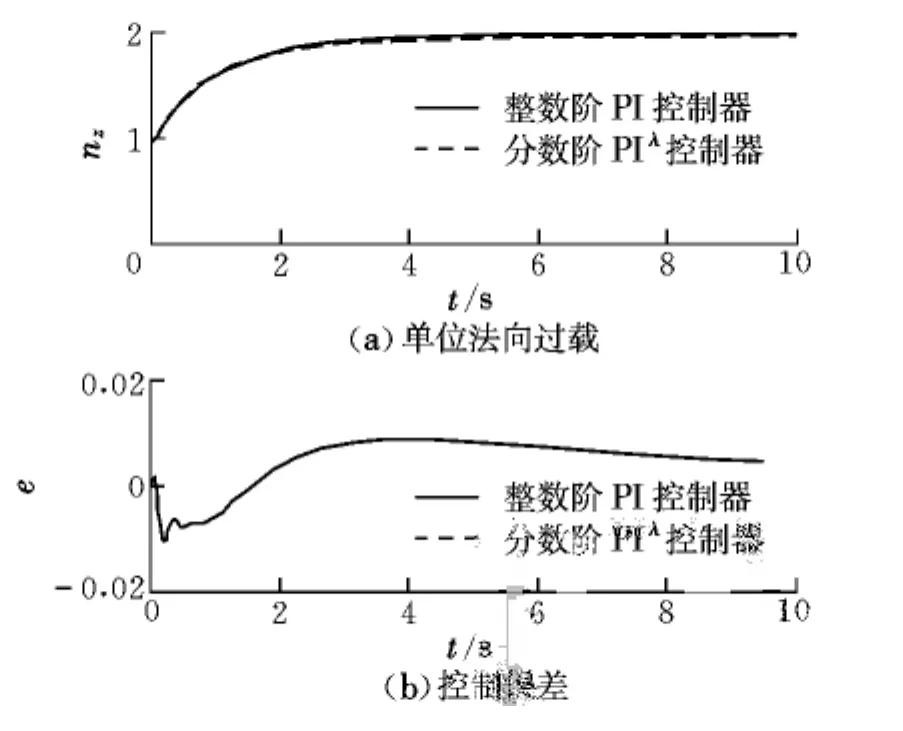
图6 飞机法向过载响应过程Fig.6 Response of aircraft normal load

由图6可知，分数阶PIλ控制器的控制增稳效果与原整数阶PI控制器几乎相同，完全满足控制增稳性能标准要求。

3.2 PIλ控制器的自动配平性能

为验证分数阶PIλ控制器的自动配平性能，采用作用时间为1～2 s，幅值为1°的方波信号模拟阵风造成的迎角扰动，扰动前后的法向过载和迎角的动态响应如图7所示。

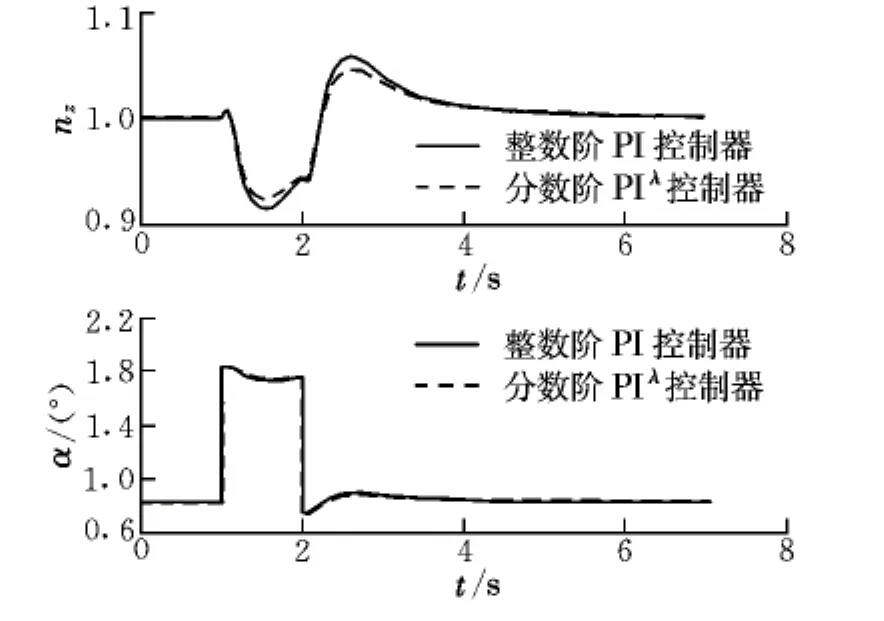
图7 PIλ控制器的自动配平性能Fig.7 Automatic trimming performance of the PIλ controller

由图7可知，两种控制器对于阵风造成的迎角扰动均可实现自动配平，但分数阶PIλ控制器的自动配平性能较整数阶PI控制器有较大提高，其法向过载扰动峰值下降了25%。因此，当飞机受误操纵或气流扰动扰动后，分数阶PIλ控制器可使飞机迅速自动配平，大大降低飞行员的劳动强度。

3.3 PIλ控制器的平飞加速性能

为验证单独操纵油门时的平飞加速性能，始终保持法向过载指令为0，油门推力指令增大13%时，两种控制器下的飞机速度、高度和法向过载的动态响应如图8所示。

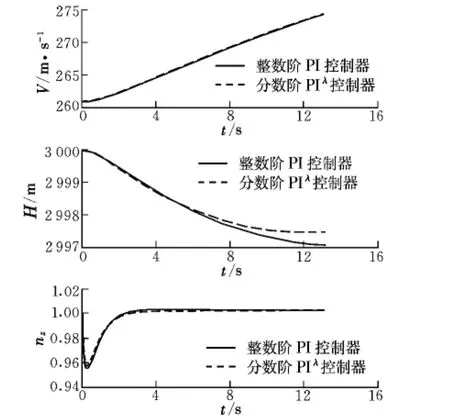
图8 飞机平飞加速性能Fig.8 Level flight acceleration performance of the aircraft

由此可知，单独增大油门推力指令而不进行推杆操纵时，两种控制器均可实现平飞加速，但相比PI控制器，PIλ控制器使飞机高度降低更少，法向过载振荡更小，即具有更优的平飞加速性能。因此，PIλ控制器可大大简化飞机平飞加减速时的操纵程序，减轻飞行员的操纵负担。

4 结束语

本文研究了分数阶PIλDμ控制器的理论基础、近似拟合方法，并进行了仿真实现，进而用于改进飞机中性速度稳定性控制律的设计，取得了较好的效果。分数阶微积分在控制领域的研究与应用还处于刚刚起步阶段，基于分数阶微积分理论的PIλDμ控制器就已经显示了良好的应用前景，并取得了较大进展。但由于起步较晚，分数阶控制的数学理论基础、分数阶控制系统建模以及分数阶控制方法等领域还有诸多空白，需要今后开展大量的研究与应用探索。

［1］ 徐鑫福.飞机飞行操纵系统［M］.北京:北京航空航天大学出版社，1989:424.

［2］ 朱呈祥，邹云.分数阶控制研究综述［J］.控制与决策，2009，24(2):161-169.

［3］ Podlubny I.Fractional-order systems and PIλDμcontrollers［J］.IEEE Transaction on Automatic Control，1999，44(1):208-214.

［4］ 王飞，雷虎民.基于分数阶微积分PDμ比例导引制导规律［J］.控制理论与应用，2010，27(1):126-129.

［5］ 张邦楚，王少锋，韩子鹏，等.飞航导弹分数阶PID控制及其数字实现［J］.宇航学报，2005，26(5):653-656.

［6］ 王海涛，董新民，王建刚.分数阶控制理论及其在飞机俯仰控制中的应用［J］.飞行力学，2011，29(5):44-48.

［7］ 薛定宇.控制系统计算机辅助设计［M］.第二版.北京:清华大学出版社，2006.

［8］ Oustaloup A，Levron F，Mathieu B，et al.Frequency-band complex noninteger differentiator:characterization and synthesis［J］.IEEE Transaction on Circuit and Systems-I:Fundamental Theory and Applications，2000，47(1):25-39.

［9］ Nguyen L T，Ogburn M E，Gilbert W P，et al.Simulator study of stall/post-stall characteristics of a fighter airplane with relaxed longitudinal static stability［R］.NASA Technical Paper 1538，Washington D C:NASA，1979.