小型固定翼飞机飞行动力学仿真
2015-12-28陈卫东宁雷刘淼群吴限德汪超亮
陈卫东,宁雷,刘淼群,吴限德,汪超亮
(1.哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨150001;2.中国科学院 定量遥感信息技术重点实验室,北京100094)
0 引言
计算机仿真是系统仿真技术、计算机技术及相关专业技术等多领域结合的产物,它随着计算机技术的发展而发展起来,并在诸多领域得到广泛的应用。飞行动力学仿真技术基于飞机飞行动力学、空气动力学以及飞行控制原理等学科,是飞机飞行仿真的关键技术[1]。
早期,由于飞机设计与制造公司无法提供准确、充足的飞行仿真所需的设计和试飞数据,飞机的飞行建模方法比较粗糙简单,模型的逼真度也较低。进入20世纪90年代后,由于航空界对飞行模拟重视程度的提高,一些大型飞机制造公司(如波音公司和空中客车公司)开始在飞机设计和试飞中同步生产出飞机飞行模拟机所需要的专用数据,使得飞行仿真建模越来越精准[2]。随着研究工作的不断深入,以及对飞机模型准确性要求的不断提高,其系统庞大、运动特性复杂、气动数据繁多的特点使得准确建立飞行动力学模型的难度越来越高[3],因此在飞机建模时,应充分考虑飞机运动特性复杂和模型数据量庞大的特点,并对模型作适当简化,以求能够准确反映飞机的实际运动特性。
本文以Y12固定翼轻型运输机为研究背景,对该飞机进行动力学仿真,验证飞机的飞行特性,同时,对其他以飞机为对象的研究工作也具有参考价值。该飞机一般为低中空、低速(马赫数0.3以内)飞行,并由升降舵、方向舵及副翼控制飞行姿态。在动力学建模时,为使仿真模型准确性更高,首先利用有限元分析软件,获得飞机的各个气动参数,并考虑风对飞行的影响,然后使用Matlab语言编写仿真程序,采用标准四阶Runge-Kutta法逐步求解飞机飞行动力学方程组,利用飞机实际飞行数据与仿真结果进行了对比。对比结果表明,该方法适用于飞机动力学仿真,获得的结果也相对准确。
1 飞机模型建立
本文以Y12飞机为背景,建立表征飞机运动规律的数学模型。在建模时假设飞机的运动为六自由度的刚体运动,将地面坐标系视为惯性参考系,并假设地面为平面;同时考虑非平静大气的作用。
将飞机质心动力学矢量方程投影到航迹坐标系中,可得到如下形式:
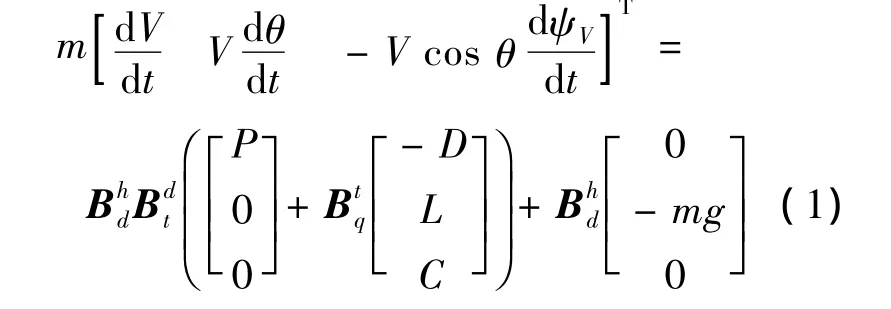
将飞机绕质心转动的动力学矢量方程投影到机体坐标系上。则方程有如下形式:
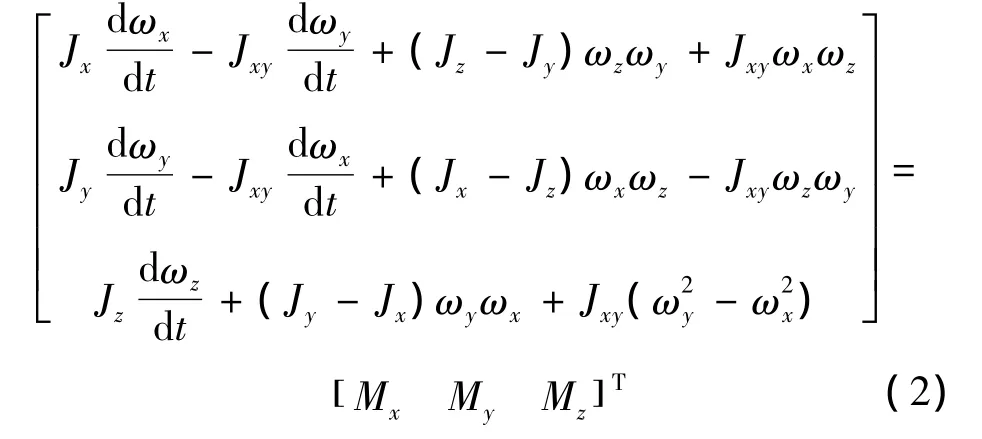
式中:Jx,Jy,Jz分别为飞机对机体坐标系各轴的转动惯量;Jxy为飞机对机体坐标系x轴和y轴的惯性积,忽略误差影响,假设Oxy为飞机对称面,则有惯性积Jyz=Jzx=0。
根据速度与位置关系,在地面坐标系中,飞机质心的运动学方程为:
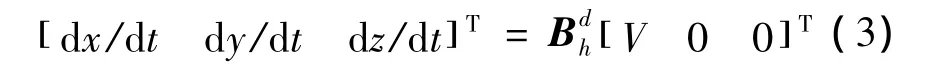
确定飞机在空中的姿态,需要建立描述飞机相对地面坐标系姿态变化的运动学方程如下:
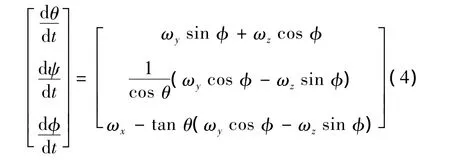
非平静大气中的仿真模型,需要考虑风对飞机飞行的影响。飞机相对地面的速度V、相对气流的速度VU与风速VW有如下关系:

其中,速度VU可表示为:
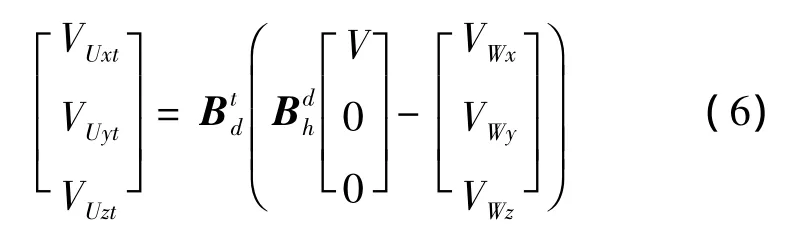
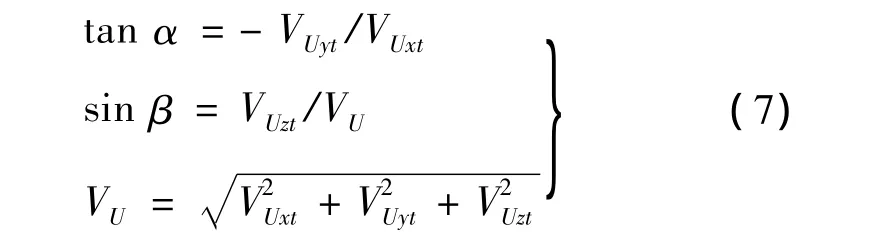
在描述飞机运动的模型中,还需有描述飞机质量变化的微分方程。其表达式为:

式中:Q为燃料消耗率,由油门开度决定[5]。
下面建立飞机仿真的大气模型。飞机工作于对流层,因此可将大气视为一种因地球引力场作用而呈固定分布的、服从玻意耳定律关系式的气体,并假设地球引力为常数。随着海拔高度的升高,大气密度从海平面处的1.225 kg/m3开始递减,利用理想气体状态方程,密度可表示为:

式中:大气压力p和温度T的具体表达式见文献[6];M0为平均空气分子量(28.964 4 kg/kmol);RS为大气常数(8 314.32 J/(kmol˙K))。
声速c依赖于大气温度,计算公式为:
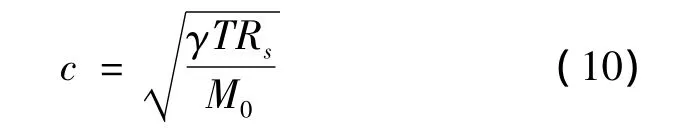
式中:γ为理想双原子气体的比热容(γ=1.4)。
以上便建立了飞机的飞行动力学模型,结合相关参数后,便可以对其进行求解。
2 作用在飞机上的气动力和力矩
作用在飞机上的空气动力沿气流坐标系分解为三个分量:阻力D、升力L和侧向力C。实验分析表明:空气动力的大小与来流的动压q和飞机的特征面积S有如下关系:
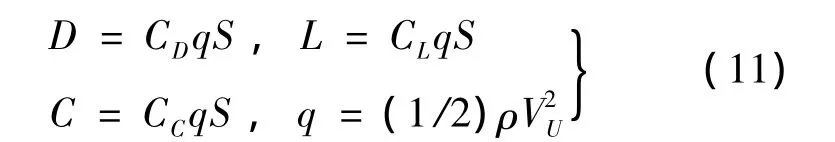
式中:CD,CL和CC分别为阻力系数、升力系数和侧向力系数。
作用在飞机上的气动力矩沿机体坐标系分解为三个分量:滚转力矩Mx、俯仰力矩My和偏航力矩Mz,可写成如下形式:

式中:Lc和Lz分别为侧向和纵向特征长度;Cl,Cn和Cm分别为滚转力矩系数、偏航力矩系数和俯仰力矩系数[7]。
本文采用计算流体力学有限元分析软件进行固定翼飞机气动特性计算。在计算时假设机翼的安装角为0°;考虑飞行的真实过程以及各种运动学参数对气动特性的影响,选取主要影响参数(如迎角、马赫数、舵偏角等)对固定翼飞机气动特性进行计算,得到诸如升力系数、阻力系数等气动参数,并将各气动参数表示成多个在不同影响因素(如侧滑角β、升降舵偏角δe)下关于马赫数Ma和迎角α的二维表格形式[8]。表1和表2分别为β与 δe均为0°时飞机的升力系数和阻力系数,其他工况由于篇幅所限未全列出。
由气动数据表可知,气动参数是多变量函数,形式比较复杂,并且在飞行仿真时需要根据采样点处的函数值,计算非采样点处的数据,因而需要进行多维函数插值计算。
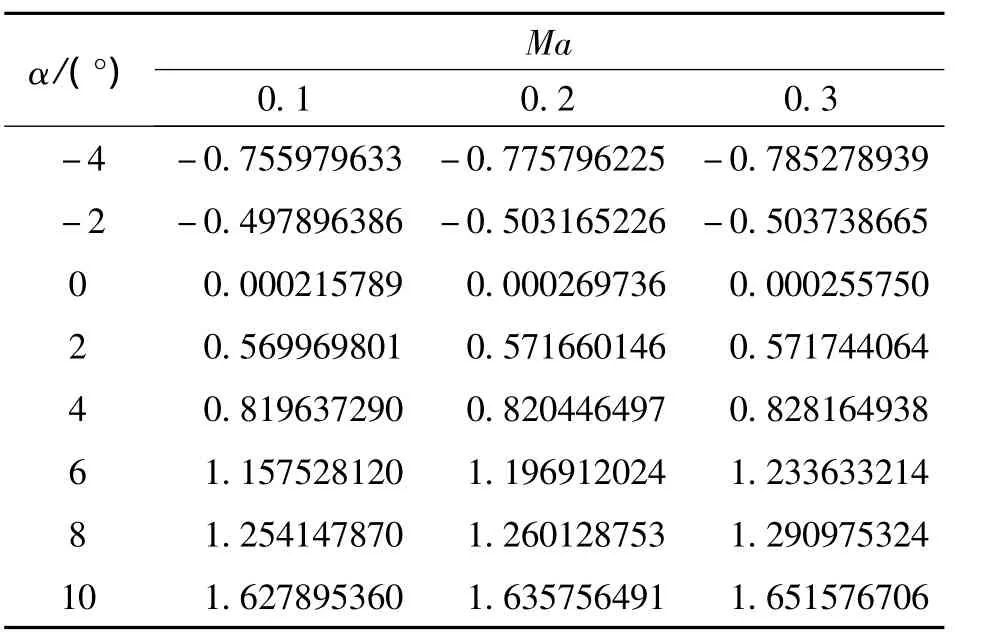
表1 β=0°,δe=0°时的升力系数Table 1 Lift coefficient with β =0°,δe=0°
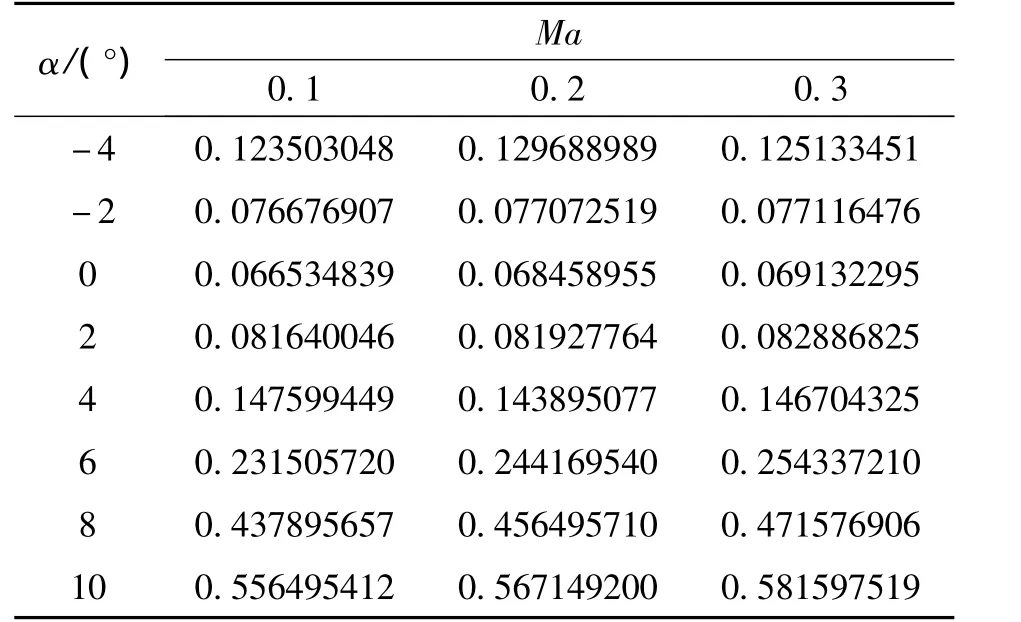
表2 β=0°,δe=0°时的阻力系数Table 2 Drag coefficient with β =0°,δe=0°
3 仿真和模型验证
本文所仿真的飞机飞行轨迹描述如下:在高度3 430 m左右定高飞行,直线平飞一段距离后,完成一个右转弯动作,并沿着平行于第一段飞行直线的轨迹返回,再完成一个左转弯,回到接近飞行初始点的位置(见图1),并重复上述动作。
仿真与数据处理程序用Matlab语言编写,首先设定仿真初始参数,然后采用标准四阶Runge-Kutta法对方程进行求解。求解完成得到结果后,与飞机飞行过程中实测数据进行对比,下面分别叙述各参数飞行试验实测数据与仿真曲线的对比结果。
图1为飞机水平轨迹对比图。由图可见,仿真飞行轨迹与实测轨迹吻合度较高,但是,实际飞行过程中的飞行环境随机因素和人为因素会带来两条曲线间的差异:飞行速度的变化使得实测曲线平均转弯半径相对较小,两个转弯动作也不可能完全相同;仿真模型对两个转弯部分设定相同的参数,曲线呈对称形状,而并不会考虑上述因素带来的误差。故可认为仿真模型能够完成飞机实际的飞行动作。
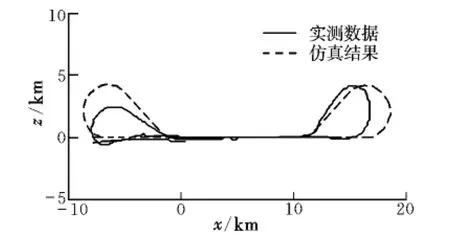
图1 水平轨迹对比Fig.1 Horizontal trajectory comparison
图2 为飞行高度的变化曲线。受到飞行环境中随机因素与人为因素的干扰,飞行试验的高度变化在一定范围内产生波动,但这种波动依然是在尽量保持高度3 430 m飞行的条件下产生的,仿真模型忽略了上述因素的干扰,对高度的保持控制较为理想,波动较小。从总体上看,仿真很好地体现了定高飞行的要求。
图3为偏航角对比图,在完成两次直线和转弯飞行的时间上,实测数据与仿真结果略有差别。这同样受到不可控因素的影响,驾驶员在驾驶飞机时速度并不能保证恒定,由图1中也可见,实测曲线在转弯处的飞行距离要小于仿真数据,因此在图3的后半段,仿真曲线的变化也会相应延后,但这并不影响整体飞行轨迹的完成和仿真对飞行特性的体现。在完成转弯过程中,偏航角发生变化,由0°变化到180°的过程中,有一个先减小再增大的过程,与图1中的轨迹正好吻合。因此,偏航角仿真能够很好地反映飞行试验中的真实情况。
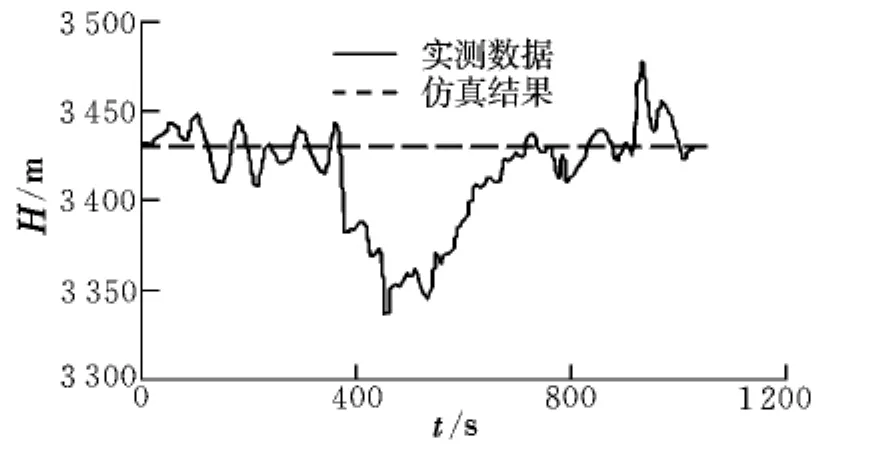
图2 飞行高度对比Fig.2 Flight altitude comparison
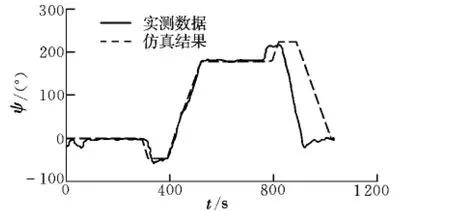
图3 偏航角对比Fig.3 Yaw angle comparison
图4 为滚转角和俯仰角对比图。由图可见,实测与仿真曲线吻合度较高,仿真结果能够极好地模拟直线平飞与转弯两个过程中偏航角和滚转角的对应变化情况。在平飞阶段,滚转角为0°,进入转弯时,滚转角发生变化,随着转弯的方向,飞机机身发生相应倾斜,图中实测与仿真曲线都体现了这种变化。与偏航角相同,在飞行仿真后段,仿真模型的飞行距离大于飞机飞行距离,转弯时滚转角的变化也相应延后。俯仰角方面,进入转弯时飞机姿态发生变化,相应的俯仰角也做出调整,俯仰角在飞机进入转弯和完成转弯时均发生变化,与飞行实测数据中的姿态略有差异,这是由驾驶员选择转弯的方式在仿真中被忽略的原因造成,但是对飞行轨迹和高度造成的影响较小,对仿真反映真实飞行规律和特点的影响也较小。
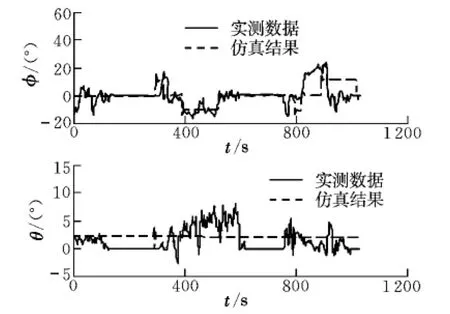
图4 滚转角和俯仰角对比Fig.4 Roll angle and pitch angle comparison
图5 为飞行速度对比图。飞机在完成上述飞行过程时,驾驶员的驾驶习惯及其他环境干扰因素使得速度的波动较大,但是依然能够保持在60 m/s至70 m/s的范围内,在中后段的飞行中,飞机速度随着波动逐渐变大,因此造成了一系列如滚转角、偏航角等仿真结果较飞行实测数据延迟的效果,这些误差也与图1中转弯处飞机平均转弯半径小于仿真结果的情况相符。仿真抛开了随机因素和人为因素的影响,设定飞行速度为63 m/s,且仿真全过程中保持较好,仅在转弯时稍有波动,总体速度与实测的平均速度相当,很好地完成了速度仿真。
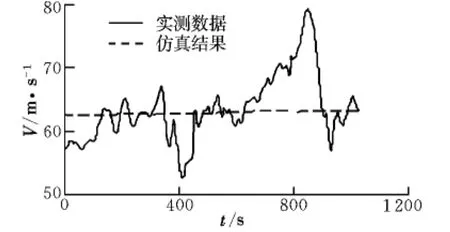
图5 飞行速度对比Fig.5 Flight velocity comparison
由以上对比结果可知,各个仿真参数曲线与飞机飞行试验数据所反映的飞行状态吻合度较高,仿真能够较好地模拟固定翼飞机飞行的基本规律与真实情况,从而可为飞机飞行性能分析与评估提供有益的参考。
4 结束语
本文研究了固定翼飞机飞行动力学仿真问题。在保证模型精确度和一定的假设与简化基础上,建立了非平静大气中固定翼飞机的飞行动力学模型;采用有限元分析软件计算固定翼飞机的气动参数,从而相对客观地描述了飞机的气动力学环境。采用Matlab程序对上述飞机模型进行仿真,并将仿真结果与飞行试验的实测数据进行对比,结果显示仿真能够体现飞机的飞行特性,从而验证了模型与仿真的有效性和正确性,为相关领域的研究提供了有益的参考。
[1] 刘春,曹硕,王志超.一种固定翼飞机飞行仿真动力学组件的开发[J].计算机仿真,2013,30(4):49-53.
[2] 汪泓,谢东来.运输机飞行仿真技术及应用[M].北京:清华大学出版社,2013:114.
[3] 杨新,王小虎,申功璋,等.飞机六自由度模型及仿真研究[J].系统仿真学报,2000,12(3):210-213.
[4] 肖业伦.飞行器运动方程[M].北京:航空工业出版社,1987:14-17.
[5] 肖业伦.航空航天器运动的建模——飞行动力学的理论基础[M].北京:北京航空航天大学出版社,2003:30.
[6] Allerton D.飞行仿真原理[M].刘兴科,译.北京:电子工业出版社,2013:84-87.
[7] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2005:9.
[8] Gyllhem D,Mohseni K,Lawrence D,et al.Numerical simulation of flow around the Colorado micro aerial vehicle[R].AIAA-2005-4757,2005.
