Morse不等式的一个新证明
2015-12-28李合朋
Morse不等式的一个新证明
李合朋
(四川文理学院数学与财经学院,四川达州635000)
摘要:用Witten形变理论在带边微分流形上给出Morse不等式一个新的证明方法. 首先,说明了相切型Morse函数很自然地与带边流形的Hodge理论相结合;然后,利用Witten形变给出算子ΔT在临界点的性态,进而证明了定理.
关键词:Morse不等式;Witten形变;Hodge理论;临界点
收稿日期:2015-06-02
基金项目:四川文理学院2013年度自然科学面上项目“动力系统几何理论研究”(2013Z004Y)
作者简介:李合朋(1984—),男,河南兰考人.助教,硕士,主要从事微分几何研究.
中图分类号:O186.1文献标志码:A
不论是无边流形还是带边流形的Morse理论都已经被广泛的研究了.[1-3]80年代初,Witten提出了一套新的方法,使Morse理论重新成为焦点,这个方法被称为Witten形变.它不仅给出了经典Morse理论新的证明,而且还自然地与Thom-Smale理论相连.这套理论的量子化即后来发展的Floer理论.
处理带边流形时,通常考虑梯度与边界相截的Morse函数,然后将问题转化为无边流形,从而获得相关结论.一个自然的问题是:是否可以不借助无边流形,直接研究带边流形的Morse理论.譬如,如何运用Witten形变等等,由此考虑此类问题的量子化.
基于上述目的,发现合理的选择应该是梯度与边界相切的Morse函数.它很自然地与带边流形的Hodge理论相结合,由此,利用Witten形变给出了带边流形Morse理论新的证明.
1预备知识
1.1带边流形的Morse理论
假设(M,N=∂M)是一个n维的可定向的紧致的带边流形.g是一个度量,假设N 的邻域为N×[0,ε),度量在这个邻域上为
g=gN+dt2
记外法向量-∂/∂t为ν.
令f:M→R是一个Morse函数,满足

称之为相切型Morse函数.注意到,任何一个梯度与边界横截的函数都可以适当的形变成相切型的.
将f的临界点分为三类:内点,内向的边界点,外向的边界点.先解释一下后两者的定义,假设x∈N是f的临界点,不妨假设存在一个坐标卡y=(y1,…,yn-1,t)使得度量
以及
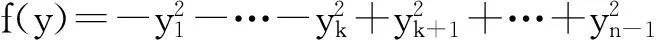
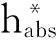
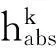


并且当k=n时,″=″成立.
于是有复形

1.2带边流形的Hodge理论与Witten变形
在带边流形上,考虑的两种同调理论H*(M,R)和H*(M,N,R),它们都有自己相应的deRham理论.令

ivdω|N=0}
(1)

v*∧δω|N=0}
(2)
这里δ是d的对偶,v*是v的对偶.
对上述两个复形,做如下Witten变换.为简单起见,着重对其中一个描述, 考虑复形

对任意T∈R,定义dT=e-TfdeTf.
证明: 利用f是相切型这一性质,容易直接验证.
因此可以定义复形
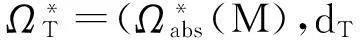
显然,这个复形定义的同调自然同构于原复形所定义的同调理论.
下面考虑该复形的Hodge理论[6],由直接计算知dT的对偶
δT=eTfδe-Tf.
定义

则由经典的Hodge理论[7]

2主要结论
假设x是非退化临界点,存在一个邻域Ux以及坐标y=(y1,…yn)使得
以及
由标准的计算,算子ΔT在Ω*的核是
当x是内点,则没有什么需要特殊处理的; 当x是内向的;则



证明的方法即把上面的“局部”观察转化为流形整体的结果.在此仅讨论x是边界点的情形,局部上有形式ωx,T,下面将适当的选取一个截断函数γ:M→R 使得它的支集在x的一个小邻域Ux内.令
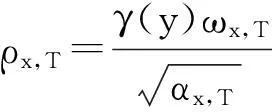
其中

引理2ivρx,T=0,ivdρx,T=0.
首先
ivωx,T=0,ivdωx,T=0,
所以显然
ivρx,T=0.
若选取的γ满足
ivdγ=0.
(3)
则显然有ivdρx,T=0,于是引理得证.
下面构造一个γ使得(3)成立.

γ(y)=γ(y′,t)=γ1(y′)γ2(t).
此函数显然满足(3),从而证明了定理3.
由此命题出发,证明所有相关的Morse理论全是标准的.
参考文献:
[1] Bismut J M.TheWittenComplexandtheDegenerateMorseInequalities[J]. Journal of Differential Geometry,1986(3):207-240.
[2] Zhang Gongqing, Liu Jiaquan.Morsetheoryundergeneralboundarycoditions[J]. Systems Science and Mathematical Sciences,1991(1):78-83.
[3] Zhou Jianwei.TheWittencomplexandtheMorseinequalities[J].Journal of Suzhou university,1999(4):8-11.
[4] J.Milnor.Morsetheory[M]. Princeton:Princeton University Press,1963:27-31.
[5] M. Taylor.PartialdierentialequationsI[M].New York:Springer-Verlag,1997:368-370.
[6] F.W.Warner.FoundationsofdierentiablemanifoldsandLiegroups[M]. New York: Springer-Verlag,1983:222-249.
[7] 伍鸿熙,陈维桓.黎曼几何选讲[M].北京:北京大学出版社,1993:7-13.
[8] Weiping Zhang.LecturesonChern-WeiltheoryandWittendeformation[M].Tianjin:Nankai Treats in Mathematics,Vol.4,World Scientic,2001:59-72.
[责任编辑范藻]
A New Proof of Morse Inequalities
LI Hepeng
(Mathematics and Finance School of Sichuan University of Arts and Science, Dazhou Sichuan 635000, China)
Abstract:Witten deformation theory is applied to a new proof of the Morse inequalities on a differentiable manifold with boundary. It is explained that the tangential Morse function is naturally combined with the Hodge theory of the manifold with boundary, then, Witten deformation gives the behavior of ΔT at critical point, and thus the theorem is proved.
Key words:Morse inequalities; Witten deformation; Hodge theory; critical point
