无偿援助金融支持的幸福感分析
2015-12-28李爱民
无偿援助金融支持的幸福感分析
李爱民
(四川文理学院数学与财经学院,四川达州635000)
摘要:根据Uzawa-Lucas模型,把农村经济分为物质资本和非物质生产部门(重点讨论人力资本),首先确定五个假设条件,包括了消费者的效用函数和一些因素的运动方程;然后构建无偿援助模型的优化形式,从幸福感外生和内生两种情况探讨无偿援助模型的最优均衡分析;最后得到相关的定理和结论,主要体现有力促进经济发展,加强金融支持高效率,突出幸福感获得的来源.
关键词:生产函数;物质资本;人力资本;金融支持;幸福感
收稿日期:2015-03-20
基金项目:2013年度四川循环经济研究中心项目“农业循环经济金融支持的预警模型”(XHJJ-1307);四川文理学院2013年度教育教学改革研究项目“理工专业的高等数学教育教学改革”(2013JY11)
作者简介:李爱民(1978—),男,河南新乡人.讲师,硕士,主要从事泛函分析与数理经济研究.
中图分类号:O29文献标志码:A
0引 言
根据文献[1],金融支持是发展农业循环经济政策体系的重要组成部分,在全面推进农业循环经济发展过程中具有着重要作用,金融支持影响着农业循环经济的实施程度,我国农业循环经济金融支持效率仍存在很大优化空间.根据文献[2]-[11],参考Uzawa-lucas模型,可以假定农村经济存在两个不同的生产部门:物质生产部门和非物质生产部门.结合我国新农村建设,新农村建设成败的关键在于农民素质,重在农村人力资源的建设,因而本文非物质生产部门重点探讨人力资本.根据公共物品外部经济的特征,对于农业经济的发展,合理的金融资本是能带来正外部性的,它更能促进农业循环经济的发展.因此,根据[5]-[8],金融支持主要包括无偿金融支持与有偿金融支持.本文主要构建关于幸福感的效用函数,进一步探讨农业循环经济与无偿援助金融支持的关系与模型,论述农业金融支持的相关因素,然后寻找它们的均衡结果,提出相关策略.
1有关概念和函数关系
关于中国农业国情,在2013年,中国农产品进出口额为1866.9亿美元,全年货物进出口总额为41600亿美元,中国农产品进出口额占货物进出口总额的比例不超过5%,因而可以把农业循环经济看成一个封闭经济系统.依据中国最具幸福感城市推选活动的结果显示,幸福指数测评得分最高的不是上海、北京、深圳等经济最富裕的城市,而是杭州、成都这些以休闲生活见长的城市,因而本文通过休闲表示幸福感.参照文献[8]-[17],有以下假设与函数关系:
假设1:一个由具有无限期寿命的同质消费者组成的封闭经济体,每个人既是生产者又是消费者,无人口增长,人口和最终产品价格均设定为1标准化单位.
(2.1)式中,σ为产品消费对消费者效用的影响程度,是消费跨期替代弹性的倒数,θ为金融支持对消费者效用的影响程度.对于这两方面,消费者可以获得递增的效用,边际效用递减,即有UC>0,UF>0,UCC<0,UFF<0.
假设3:假定最终产品的生产函数Y为柯布—道格拉斯形式,人力资本H投入到物质生产部门的比例为u(其余部分用于人力资本自身的积累),产出方程表示为:
Y=AKα(u(1-F)H)1-α,
(2.2)
A(>0)表示一般性生产力技术水平,可视为一系列制度因素,如政府行为、 法律体系和产权安排等的函数,K为实物资本,α为实物资本的产出弹性.
假设4:假设物质产品部门的产出除了用来消费,其余都用来作为物质资本进行投资再生产,设定物质资本折旧率为φ,并且有金融支持m,则有物质资本的运动方程:
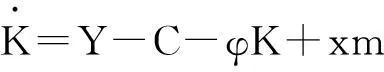
(2.3)
其中,xm表示变化的金融支持.
假设5:人力资本H的积累不但可以为经济增长提供动力,而且还能引进高质量的金融支持,从而促进可持续发展的实现.设定人力资本开发部门的产出与实际投入到该部门的人力资本线性相关, 其生产力参数为δ(δ>0),则有人力资本的积累方程:
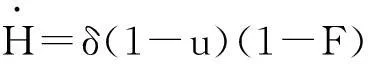
(2.4)
2幸福外生的无偿援助模型的最优均衡分析
结合上面的假设,有如下的优化形式:


作Hamilton 函数:V=U(C,F)+λ1(Y-C-φK+xm)+λ2δ(1-u)(1-F)H,解得最优化条件:
Euler方程有:
和横截性条件
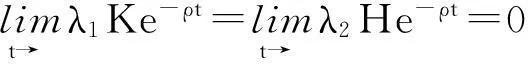
(3.4)
结合(3.1)、(3.2)、(3.3),得到:
由于经济在均衡增长轨道上运行时,所有实际变量都按常数增长,又因为实物资本积累来自于新的最终产出,所以,在均衡时,有

定理1:在均衡时,由(3.5)得到,
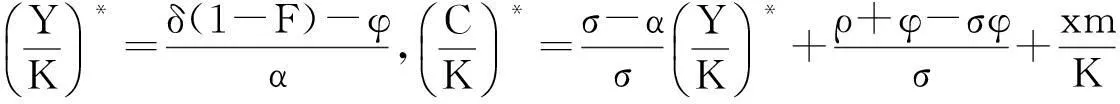
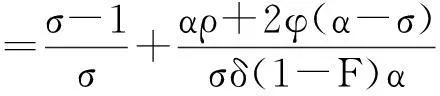
gH*=gY*=gC*=gK*
结论1:根据定理1,有:

(2)总产出、消费、实物资产的均衡增长率与金融支持无关,但是通过适当的金融支持,可以有效促进消费,间接增加生产,加快增长率达到均衡.
(3)总产出、消费、实物资产的均衡增长率增大时,在其他因素不变时,幸福感减少;其均衡增长率减小时,幸福感可以提高.

3幸福内生的无偿援助模型的最优均衡分析
如使消费和金融支持的幸福度同时达到最优化,需要把幸福度作为内生参数考虑.结合上面的假设,有如下的优化形式:

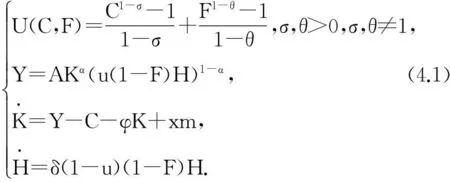
作Hamilton 函数:V=U(C,F)+λ1(Y-C-φK+xm)+λ2δ(1-u)(1-F)H,解得最优化条件:
Euler方程和横截性条件同(3.3)、(3.4).
结合(4.2)和(3.3),得到:
定理2: 类似幸福外生的无偿援助模型,在均衡时,由(4.3)得到,


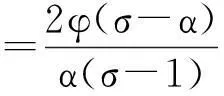
结论2:根据定理2,有:
(a)与结论1的(1)、(2)相同.
(b)在均衡时,生产力资本比、消费资本比与幸福感负相关,人力资本份额、生产力参数与幸福感正相关,时间贴现率与幸福感负相关.因而提高农业的人力资本和生产力水平是非常重要的.

参考文献:
[1] 刘红林.发展循环经济中的金融支持作用与优化机制问题研究[D].保定:河北大学,2010:1-121.
[2] R.Lucas,N.Stokey.OptimalGrowthwithManyConsumers[J].J. of Economic Theory,1984(1):139-171.
[3] M. Obstfeld.EffectsofForeignResourceInflowsonSavings:AMethodologicalOverview[M].Berkeley,University of California,Berkeley,1995:18-203.
[4] 米辉,刘先忠.带休闲的Uzawa-Lucas模型[J].华中科技大学学报:自然科学版,2004(4):114-116.
[5] 刘仙菱.论农村产业结构的调整[J].河北大学学报:哲学社会科学版,1987(3):119-123.
[6] 中华人民共和国财政部.公共财政与百姓生活[M].北京:中国财政经济出版社,2007:1-56.
[7] 李思维,孟婷.农户分层视野下的可持续发展及金融支持研究——基于可持续生计框架的个案分析[J].财经理论与实践,2013(5):25-30.
[8] 史宝玉,刘景军.新农村建设人力资本开发利用提升策略研究[J].湖南社会科学,2014(1):185-187.
[9] 李燕.国外经济援助对经济增长的影响分析[D].武汉:华中师范大学,2006:245-295.
[10]Forster B A.Optimalcapitalaccumulationinapollutedenvironment[J]. Southern Economic Journal,1973(39): 544-547.
[11]龚六堂,苗建军.动态经济学方法[M].北京:北京大学出版社,2002:245-295.
[12]涂正革.工业二氧化硫排放的影子价格:一个新的分析框架[J].经济学,2009(1):259-282.
[13]何正霞,许士春.考虑污染控制、技术进步和人力资本积累下的经济可持续增长[J].数学的实践与认识,2011(18):1-8.
[14]范定祥,廖进中,欧绍华.排放强度约束下的最优经济增长分析[J].系统工程,2012(6):77-81.
[15]王鹏.收入差距对我国居民幸福感的影响研究[D].成都:西南财经大学,2012:27-130.
[16]方先明,孙爱军,曹源芳.基于空间模型的金融支持与经济增长研究——来自中国省域1998~2008年的证据[J].金融研究,2010(10):68-82.
[17]Nancy L. Stokey.AreThereLimitstoGrowth?[J].International Economic Review,1998,39(1):1-31.
[18]黄菁.环境污染、人力资本与内生经济增长:一个简单的模型[J].南方经济,2009(4):3-11,67.
[责任编辑范藻]
Happiness analysis on the financial support of non-reimbursable assistance
LI Aimin
(Mathematics and Finance School of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000, China)
Abstract:The financial support plays an important role in promoting the development of agricultural circular economy wholly. However, the efficiency of financial support of agricultural circular economy in China still has great space optimization and it has great significance to study happiness. According to the Uzawa-Lucas model, the rural economy is divided into material production sector and non-material production sector (focusing on human capital). Firstly the five assumption conditions are determined, including the utility function of consumer and the motion equations of some factors; then the optimization is constructed on non-reimbursable assistance, its analysis of optimal equilibrium is from exogenous and endogenous situation on happiness; finally some theorems and conclusions are got that mainly is to promote economic development and strengthen the financial support for high efficiency and point out the source of happiness.
Key words:production function; physical capital; human capital; financial support; happiness
