XY模型几何量子关联临界行为与路径关系研究
2018-08-15张修兴
张修兴,郭 庆
(1.渭南师范学院物理系,陕西渭南714099;2.国网山西电力调度控制中心,山西太原030020)
多体系统的量子相变一直是人们研究的热点问题[1],有关纠缠度的临界行为和系统相变点的关系引起人们的广泛关注[2-5]。Osborne等通过研究XY模型中两自旋间的纠缠,发现在临界点附近量子纠缠出现尖峰[2]。Vidal等研究了由L个自旋组成的自旋团簇(spin block)间的纠缠,结果表明L非常大的情况下,在相变点附近纠缠熵成对数发散[5]。
除了纠缠度,人们还利用其它形式的量子关联来表征系统发生的量子相变,比如:量子失协[6-7]、保真度[8]、纠缠熵[9]等。其中,量子失协因为可以描述系统所包含的所有非经典关联,所以它和量子相变的关系引起了人们的特别关注[10]。Werlang等人研究表明:即使在有限温度下量子失协也可以用来探测系统的相变点[11]。虽然量子失协有很多超越其他量子关联的优点,但是它的求解比较复杂,而且很多系统中无法给出其解析表达式,这给研究带来很多不便。后来,Dakic等引入几何量子关联(Geomet⁃ric Measure of Quantum Discord-GMQD)的概念[12]。GMQD不但可以描述系统中包含的所有量子关联,而且可以求出其解析表达式。这为人们提供了一个研究量子关联和量子相变关系的有效工具[13-17]。Shan等的研究结果证明GMQD可以刻画系统中发生的拓扑相变[16]。Fan等研究了阻错海森堡链(Frustrated Heisenberg Chain)的GMQD,结果表明对于有限大小的量子系统,GMQD也可以有效的探测其相变点[17]。
目前,物理量在量子多临界点附近的行为也是研究的热点。Patra等研究了三相点附近几何相位的标度行为[18],结果表明:几何相位的标度行为和趋于临界点的路径存在密切的关系。Dutta等在XY模型中,研究了保真度在量子多临界点的行为[19]。据我们所知,GMQD在量子多临界点附近的行为还没有被研究。特别地,临界点附近GMQD的行为和趋于该临界点的路径关系仍然是一个开放问题。受这些工作的启发,我们研究以不同路径趋于临界点时,GMQD的临界行为。结果表明,GMQD及其一阶导数在多临界点附近的行为和趋于该点的路径参数α有关;它们在Ising临界点附近的行为与趋于该临界点的路径参数无关。
1 模型和主方程
图1为XY模型的基态相图。其中,A、B为系统的三相点。通过A、B两点的垂线为顺磁相和铁磁相的分界线。通过A、B两点的实线为各向异性临界线。

图1 模型的基态相图
XY模型的哈密顿量可以写为:


沿如下路径趋于系统的临界点:其中,γ=0,h=1对应于系统的三临界点;γ=21α,h=-1为系统的Ising临界点。
在具体研究几何量子失协临界行为之前,我们先把系统哈密顿量完全对角化。首先对(1)进行Jor⁃dan-Wigner变换[1]可得:

对(3)中算符进行傅里叶变换和波戈留波夫变换,系统的哈密顿量可以写成完全对角化的形式:


2 最近邻自旋间的量子关联
最近邻自旋间的约化密度矩阵为:

根据文献[14],密度矩阵(6)的矩阵元可以用自旋关联函数表示:

自旋关联函数的解析表达式:
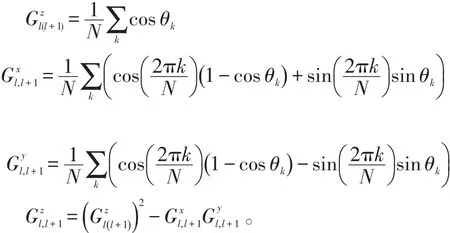
接下来,我们主要计算两自旋间的关联函数。在布洛赫表象下,密度矩阵(6)可以表示为:

根据文献[14],几何量子关联利用下式计算

可得基态GMQD:

3 几何量子关联的临界行为
我们主要研究以不同路径趋近于临界点时,GMQD的临界行为。图2给出的是以不同路径α趋于临界点时,GMQD在多临界点附近的行为。系统的大小为N=1001。从图中可以看出,路径参数α不同,GMQD的行为也不同。当α比较小时,GMQD在多临界点随各向异性参数的增大成振荡行为,并且α越小,振荡现象越明显。随着α增大,振荡行为逐渐减弱;当路径参数超过临界值α=2后,几何量子失协随γ单调增加。

图2 GMQD在多临界点附近的行为
图3给出的是以不同方式趋于Ising临界点时GMQD的行为。系统的大小为N=1001。从图中可以看出对于任意的α,GMQD在随各向异性参数γ变化的过程中出现两个极大值,一个极小值。结合等式(1)和(2)可以看出:第二个峰准确地对应于h=-1的Ising临界点;极小值对应于(γ =1,h=0),即:XX模型。由此,我们推断利用GMQD可以表征XY模型的Ising临界点。

图3 GMQD趋于Ising临界点时GMQD的行为
为了更加清楚地理解GMQD的临界行为,我们研究GMQD的一阶导数dG/dγ随各向异性参数γ的变化。图4给出的是对于确定的路径参数α<2(α=0.5,1.5),系统大小 N改变时 (N=1001,2001,3001,4001),dG/dγ在多临界点(γ=0,h=1)附近随各向异性参数γ的变化。从图中可以看出,dG/dγ随着γ的增大表现出振荡行为,并且随着α的增大峰值呈现出一定的周期性(α=1.5)。对于确定的α(α=1.5),N越大相邻峰之间的间隔越小,最高峰越靠近多临界点。实际上GMQD一阶导数的振荡行为说明:GMQD不能完全准确地表征系统的多临界点,它所刻画的是系统的准临界点[18]。

图4 α<2时dG/dγ在多临界点附近的行为
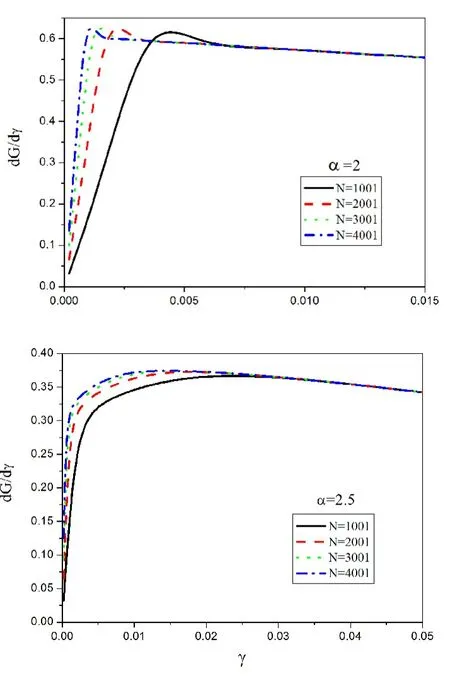
图5 α≥2时dG/dγ在多临界点附近的行为
图5给出的是对于确定的路径参数α≥2(α=2,2.5),系统大小 N改变时(N=1001,2001,3001,4001),dG/dγ在多临界点(γ=0,h=1)附近随各向异性参数γ的变化。从图中可以看出,随着γ的增大dG/dγ先增大到一个最大值,然后随着γ的增大而单调减小。N越大峰值越大,并且最高峰离量子多临界点的距离也越近。
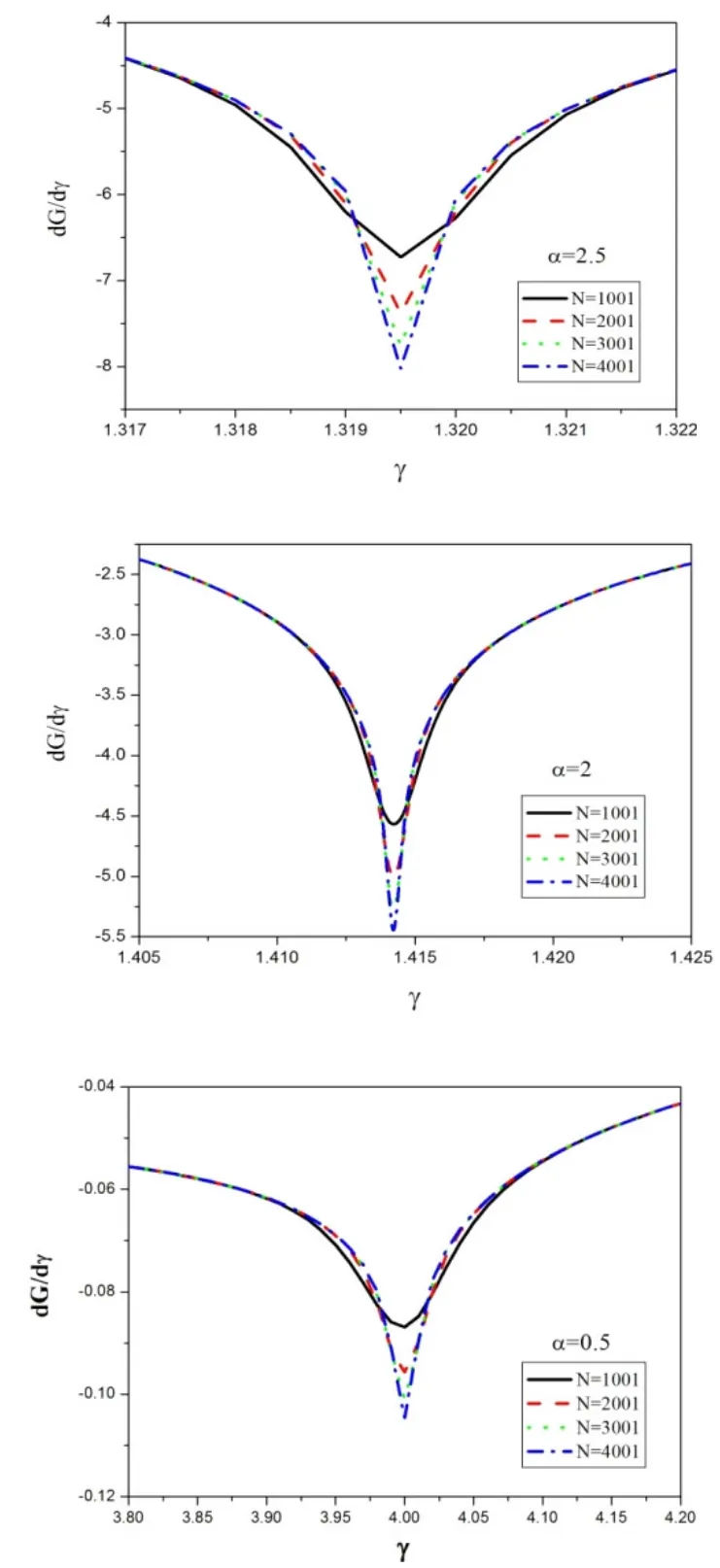

图6 在Ising临界点时GMQD的行为
图6给出的是对于确定的路径参数α(α=0.5,1.5,2,2.5),系统大小N改变时(N=1001,2001,3001,4001),dG/dγ在Ising临界点附近随各向异性参数γ的变化。从图中可以看出,不论α取什么值,dG/dγ在随γ变化的过程中只出现一个最小值。可以证明该最小值的位置是Ising临界点。
4 结论
GMQD在三临界点附近的行为和趋于该点的路径参数α有关。当α<2时,GMQD及其一阶导数在三临界点附近呈现振荡行为,而且振荡的最高峰值随着系统中自旋数目的增大而靠近多临界点。这说明GMQD不能准确表征系统的多临界点,它所表征的是系统的准临界点;当α≥2时,振荡行为消失,GMQD的一阶导数在多临界点附近只出现一个极大值。在Ising临界点,GMQD及其一阶导数出现极值,且和路径参数α无关,这说明GMQD可以准确表征系统的Ising临界点。研究结果对利用几何量子关联刻画量子相变现象提供一定的理论参考。
