带有扰动的时滞系统的稳定性分析

盛春红

沈阳化工大学科亚学院

带有扰动的时滞系统的稳定性分析

盛春红

沈阳化工大学科亚学院

采用新的Lyapunov函数方法，获得了具有非线性扰动的时滞系统稳定性充分条件，引入了新的引理，利用线性矩阵不等式技术（LMI），得到了更好的保守性结果，数值仿真例子说明了方法的可行性和有效性。

稳定性分析；时变时滞系统；Lyapunov第二方法；线性矩阵不等式(LMI)

引言

时滞现象存在于实际工程系统中，带有一定程度的时间延迟现象。时滞系统更加的接近于实际系统，例如，各种工业成产环节，传输系统等，介于很多实际系统都是非线性的系统，而且复杂度非常大，因此，用精确的数学模型来描述这些由微分方程表达的动态系统是很困难的，进而找到一种既接近于实际工程系统又方便研究的数学微分方程模型就显得非常有必要，所以研究带有扰动的时滞系统具有深刻的理论意义和研究价值，破坏系统稳定性的主要根源就是时滞，对系统的分析和综合带来很大的影响，现在对带有扰动的时滞系统的稳定性分析和控制器设计，已经成为现代控制理论的研究热门。

一、系统描述

考虑如下时滞系统：

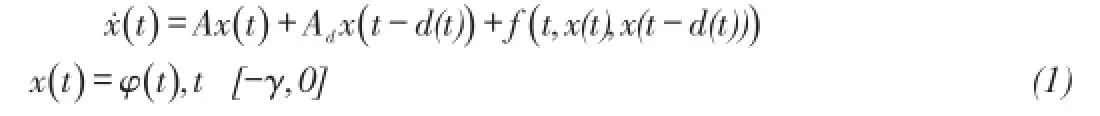
非线性项满足如下条件：

其中，G,H为给定的常值矩阵。

引理1(Liu[1,2])

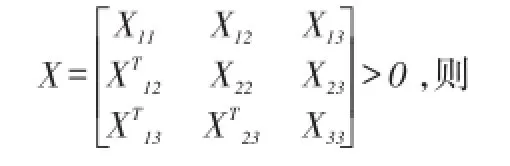
引理2对任意的实向量a，b和任意适维给定的矩阵Z＞0，有如下矩阵不等式成立：

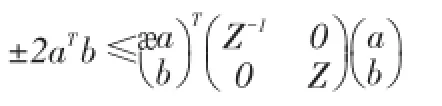
首先，考虑时滞系统(1)：

引入如下形式的李雅普诺夫函数(5)，采用线性矩阵不等式(LMI)技术得到系统(4)的渐进稳定的充分条件:

其中：

其中P＞0,Q1＞0,Q2＞0,R1＞0.

二、主要结论

给出时滞系统(1)的稳定性充分条件，得到如下定理。

定理在零输入的条件下，如果存在标量ε1＞0，及P＞0, Q1＞0,Q2＞0,R1＞0,Z1＞0，Z2＞0，以及适当给定的矩阵H，H2，H3，X11，X12，X13，X22，X23，使得如下线性矩阵不等式(LMI) (7)成立,则时滞系统(1)是渐进稳定的.

其中

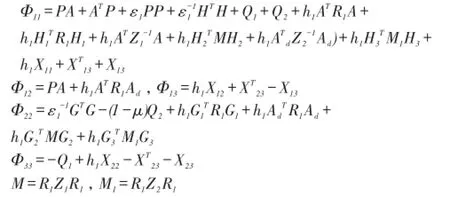
证明选择形如(6)的Lyapunov函数V(xt).引入系统(1)，对文中所选择的Lyapunov函数V(xt)(6)求导可得，

由引理2得，

由(8)～(17)，得

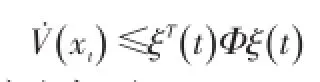
则时滞系统(1)是渐进稳定的。

数值仿真

考虑时滞系统系统(1)，其中

令μ=0.8，根据定理求解式矩阵不等式（LMI）(7)，得h=2.0418。

上述数值仿真结果表明本文定理是正确的，由于采用了新的Lyapunov函数，引入了更多的自由矩阵，增加了解得可行域，从而具有了更好的保守结果。

[1]LiuPL.Furtherimprovementondelay-range-dependentstability⁃resultsforlinearsystemswithintervaltime-varyingdelays.ISATrans2013. http://dx.doi.org/10.1016/j.isatra.2013.07.006(in press).

[2]LiuPL.Robuststabilityofintervaldynamicsystemswithmultiple⁃time-delays.Electron Lett2001；37:1269-70.

[3]LiuPL.Statefeedbackstabilizationoftime-varyingdelayuncer⁃tainsystems:adelaydecompositionapproach.LinearAlgebraAppl2013；438(5):2188-209.

[4]汤红吉.不确定时滞系统的鲁棒控制.2005,4.

[5]张金会,不确定时滞系统的鲁棒控制研究.206,12.

[6]LamJ,GaoH,WangC.Stabilityanalysisforcontinuoussystemswith⁃twoadditivetime-varyingdelaycomponents.SystControlLett2007；56(1): 16-24.

4.2 电除尘参数

从表1数据可以看出，二次电压最高80KV,最低61KV(额定值80KV)；二次电流接近额定值（一电场二次电流额定为1600mA,二电场二次电流额定为1400mA，三电场二次电流额定为1200mA，四电场二次电流额定为1000mA），设备运行状态良好、稳定，电除尘出口粉尘浓度排放在运行过程中没有超标过。