联手方程解难题

张萍

勾股定理是用代数思想解决几何问题的重要工具，方程是解决数学问题的另一重要工具，两者的有机结合，能轻松解决许多数学问题.下面，我们依旧利用前文中引用的教材例题，深入探讨如何将勾股定理和方程联手解题.

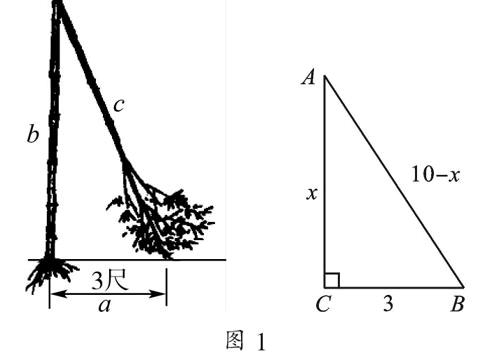
原题   （苏科版教材八上第86页例1）《九章算术》中有一道“折竹”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”题意是：一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？

【点评】勾股定理本身就是一个关于直角三角形三边长的数学等式，我们又知道含有未知数的等式就是方程，故如果用变量表示出直角三角形边长的话，就可利用勾股定理列出该变量的方程，从而解决相应问题.

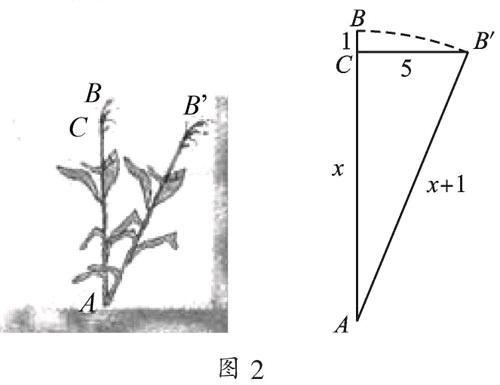
应用一：《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.问水深、葭长各几何？”题意是：有一个池塘，宽10尺，一棵芦苇生长在它的中央，高出水面1尺.如果把该芦苇沿水池边垂直的方向拉向岸边，那么芦苇的顶部恰好碰到岸边.水深和芦苇长各多少尺？

【分析】我们可以将其转化为几何图形，如图2所示，根据题意，可知B′C=5尺，可设水深AC=x尺，表示出芦苇长AB′=（x+1）尺，根据勾股定理建立方程，求出方程的解，即可得到水深和芦苇长.

解：设水深为x尺，则芦苇长为（x+1）尺.由勾股定理得x2+52=（x+1）2，解得x=12，所以水深12尺，芦苇长13尺.

【点评】利用勾股定理解决生活中的实际问题，重要的是将实际问题转化成数学模型（直角三角形模型），将实际问题转化为定理中的“形”，再转化为“数”.当已知直角三角形一边长度以及另外两边间的关系时，可根据两边间关系设出未知量，从而表示出两边，再由勾股定理列方程求解.

应用二：如图3，有一张直角三角形纸片ABC，两直角边AC=6 cm，BC=8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，你能求出CD的长吗？

【分析】由折叠的性质知CD=DE，AC=AE.根据题意，在Rt△BDE中运用勾股定理列方程，从而求出DE.

解：设CD=x cm，由题意知DE=x cm，

BD=（8-x） cm，AE=AC=6 cm.

在Rt△ABC中，由勾股定理得：

AB2=AC2+BC2=100 cm2，所以AB=10 cm，

于是BE=10-6=4 cm.

在Rt△BDE中，由勾股定理得：42+x2=（8-x）2，解得x=3.

所以CD的长为3 cm.

【点评】本题有两个难点，一是折叠前后的三角形之间对应边的转化，二是在Rt△BDE中用勾股定理时必须用方程思想，勾股定理联手方程在折叠问题中有广泛的应用.

变式   如图4，在矩形ABCD中，AB=8，BC=4，将矩形沿对角线AC折叠，点D落在D′处，求重叠部分△AFC的面积.

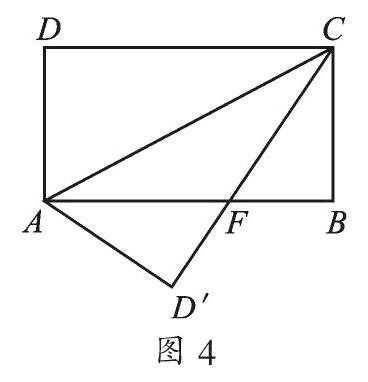
【分析】矩形翻折后易知AF=FC，利用直角三角形BFC，用勾股定理求出CF的长，也就是AF的长，继而利用三角形面积公式求△AFC的面积.

解：设AF=x，

根据题意，矩形沿对角线AC对折后有，

∠D′=∠B=90°，∠AFD′=∠CFB，BC=AD′，

∴△AD′F≌△CBF，

∴CF=AF=x，∴BF=8-x，

在Rt△BCF中有：BC2+BF2=FC2，

即42+（8-x）2=x2，

解得：x=5.

【点评】折叠问题是中考中常出现的问题，可锁定一个直角三角形，找出折叠前后相等的量，再设出未知量，表示出三边，勾股定理与方程再度完美联手.

应用三：如图5，△ABC中，AB=13，AC=15，BC=14，求△ABC的面积.

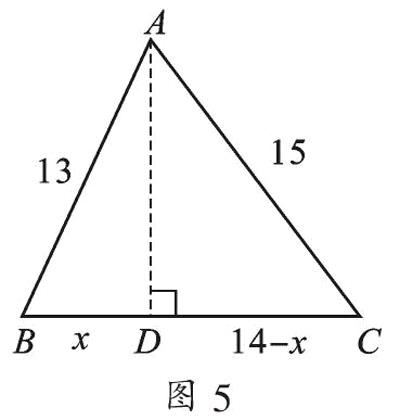
【分析】要求△ABC的面积，可过点A作BC边上的高，那么就有两个直角三角形△ABD和△ACD，AD是这两个直角三角形的公共边，可设BD长为x，分别在△ABD和△ACD中用勾股定理表示出AD的长，列出方程，求得BD的长，再根据勾股定理求得AD的长，从而求出三角形的面积.

解：作BC边上的高AD.

设BD=x，则CD=14-x.

在Rt△ABD中，由勾股定理得，

AD2=AB2-BD2=132-x2.

在Rt△ACD中，由勾股定理得，

AD2=AC2-CD2=152-（14-x）2，

可得132-x2=152-（14-x）2，解得x=5，

则AD2=132-x2=144，所以AD=12

【点评】△ABC不是一个直角三角形，求三角形的面积就要先求出三角形的高，而高可以把这个三角形分成两个直角三角形.两个三角形中都有两个未知量，并且未知量不能用同一个未知数表示，所以必须两次应用勾股定理列出两个关系式，从而求得三角形的高和面积.解决本题的关键是利用两个直角三角形的公共边建立方程.

方程思想是数学中的一种重要思想，而勾股定理反映的直角三角形三边的关系正是构建方程的基础，故与勾股定理有关的许多问题的解决都要跟方程相组合.所以我们在平时的学习过程中，要注重培养这方面的技能、思想.

（作者单位：江苏省常州市兰陵中学）