江苏省常州市兰陵中学“勾股定理”测试卷
2015-12-28丁峰
丁峰
一、 选择题
1. Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( ).
A. 8 B. 4 C. 6 D. 无法计算
2. 由下列条件不能判定△ABC为直角三角形的是( ).
A. ∠A+∠B=∠C B. ∠A∶∠B∶∠C=1∶3∶2
C. (b+c)(b-c)=a2 D. a=3+k,b=4+k,c=5+k(k>0)
3. 已知一个直角的两边长分别为3和4,则第三边长的平方是( ).
A. 25 B. 5 C. 7 D. 7或25
4. 如图,长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( ).
A. 6 cm2 B. 8 cm2 C. 10 cm2 D. 12 cm2
5. 如图,某公司举行周年庆典,准备在门口长25 m,高7 m的台阶上铺设红地毯,已知台阶的宽为3 m,则共需购买多少m2的红地毯( ).
A. 21 B. 75 C. 93 D. 96
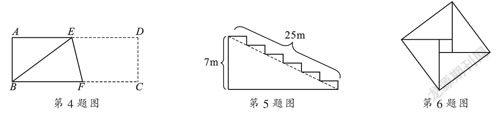
6. 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是( ).
A. 4 B. 6 C. 8 D. 10
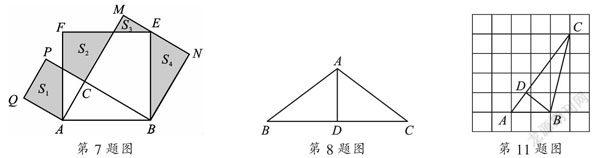
7. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( ).
A. 14 B. 16 C. 18 D. 20
二、 填空题
8. 如图,等腰△ABC的底边BC为16,底边上的高AD为6,则腰AB的长为________.
9. 四根小木棒的长分别为5 cm,8 cm,12 cm,13 cm,任选三根组成三角形,其中有________个直角三角形.
10. 如果直角三角形的三边长为10、6、x,则最短边上的高为________.
11. 如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为________.
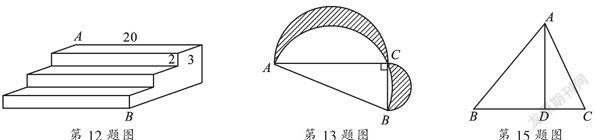
12. 如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是________.
13. 如图,Rt△ABC中,AC=12,BC=5,分别以AB,AC,BC为直径作半圆,则图中阴影部分的面积为________.
14. △ABC,AB=AC=10 cm,BC=16 cm,一动点P在底边上从B向C以2 cm/s的速度移动,当点P运动到PA与腰垂直的位置时,点P运动的时间为________.
三、 解答题
15. 如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,求AC2的值.
16. 已知:如图,有一块四边形土地ABCD,∠ADC=90°,AD=8 m,CD=6 m,AB=26 m,BC=24 m,求这块土地的面积S.
17. 洋洋想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多2米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
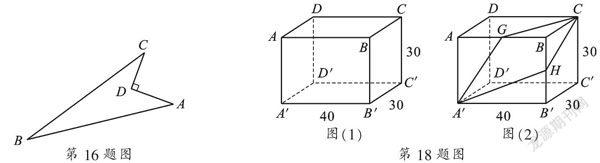
18. 图(1)、图(2)为同一长方体房间的示意图,蜘蛛在顶点A′处.
(1) 苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.
(2) 苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.
19. 如图,将矩形ABCD折叠,使A与C重合,折痕为EF,若AB=3,AD=4,问题:求折痕EF的长.
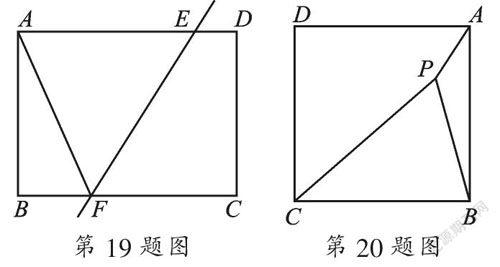
20. 阅读下列材料:
问题:如图,P为正方形ABCD内一点,且PA=1,PB=2,PC=3,求∠APB的度数.
小娜同学的想法是:设法把PA、PB、PC相对集中,于是她将△BCP绕点B顺时针旋转90°得到△BAE,然后连接PE,问题得以解决.
请根据小娜同学的想法,在图中画出图形,求出∠APB的度数.
参考答案
1. A 2. D 3. D 4. A 5. C 6. A 7. C
8. 10 9. 1 10. 8或10 11. 12. 25 13. 30
14(提示:作AD⊥BC于D,根据等腰三角形三线合一性质可得到BD的长,由勾股定理可求得AD的长,再分两种情况进行分析:①PA⊥AC;②PA⊥AB,从而可得到运动的时间.)
15. 6 16. 96 m2 17. 米
18. (1) 略;(2) 往天花板ABCD爬行的最近路线A′GC更近(提示:(1)根据“两点之间,线段最短”可知:线段A′B为最近路线;(2) Ⅰ. 将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,运用勾股定理求出A′C长;Ⅱ. 将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,运用勾股定理求出A′C长,然后将两个长度进行比较,就可解决问题)
19. 米(提示:由翻折可得到FE垂直平分AC并交于点O,那么AF=FC,易证△AEO≌△CFO那么求出OF长,乘2后就是EF长,利用直角三角形ABF求解即可.)
20. 135°(提示:根据旋转的性质知△BCP≌△BAE.由全等三角形的对应边相等、等腰三角形的判定推知△BPE是等腰直角三角形,则∠BPE=∠BEP=45°;然后由全等三角形的对应边相等、勾股定理证得∠APE=90°;最后根据图中角与角间的数量关系求得∠APB=135°)
(作者单位:江苏省常州市兰陵中学)
