巧思妙想 灵活运用
2015-12-28潘成洲
潘成洲
勾股定理是反映自然界基本规律的一条重要结论,它有着悠久的历史,在数学发展中起着重要的作用.数学思想是数学的“灵魂”,在运用勾股定理解题时,若能正确地把握数学思想方法,则可开阔思路,解题更加简便快捷.现将几种常见思想方法总结如下:
一、 数形结合思想
数形结合思想通过“以形助数,以数解形”,将数量关系和空间形式巧妙结合,使复杂问题简单化,抽象问题具体化,有助于把握数学问题的本质,发现问题中所隐含的条件.勾股定理本身就是数形结合的定理,它的验证和应用,都体现了数形结合的思想.
例1 有一直立标杆,它的上部被风吹折,杆顶着地,离杆脚20 cm,修好后又被风吹折,因新断处比前次低了5 cm,且标杆顶着地处比前次远10 cm,求标杆的高.
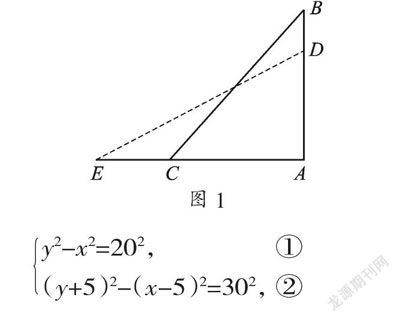
【分析】依题意作图如图1,数形结合求解.设第一次吹折后下段AB的长为x cm,上段BC的长为y cm,第二次吹折后下段AD的长为(x-5) cm,上段DE的长为(y+5) cm,依题意得,
y2-x2=202, ①(y+5)2-(x-5)2=302, ②
只要求出x+y的值即求出标杆的高而不必单独求x与y的值.
解:设第一次吹折后下段AB的长为x cm,上段BC的长为y cm,
第二次吹折后下段AD的长为(x-5) cm,
上段DE的长为(y+5) cm,依题意得,
y2-x2=202, ①(y+5)2-(x-5)2=302,②
由②-①得,10(x+y)=500,
∴x+y=50.
故标杆的高为50 cm.
【点评】利用三边的平方关系或辅助线结合生活常识可获得直角三角形,进而可求边长或面积.数形结合思想是数学中的重要思想方法,它可以使抽象的知识转化为形象的图形,从而处理起来更直观、容易,应该引起同学们的重视.
二、 方程思想
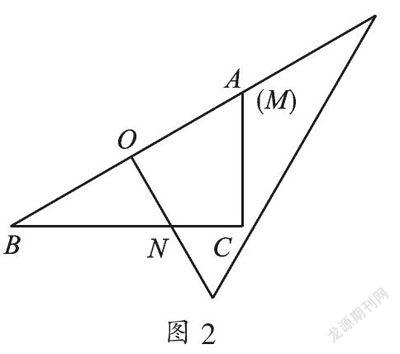
例2 在△ABC中,AB=10,AC=6,∠C=90°,点O是AB的中点,将一块直角三角板的直角顶点绕点O旋转,M、N分别为直角三角形的直角边与AC、BC的交点.
(1) 如图2,当点M与点A重合时,求BN的长.
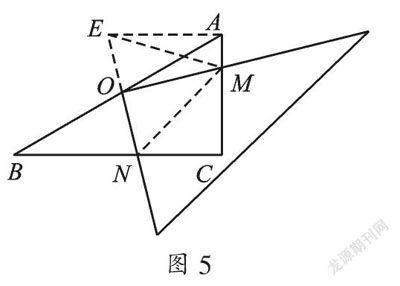
(2) 当三角板旋转到如图3所示的位置时,即点M在AC上(不与A、C重合),猜想图3中AM2、CM2、CN2、BN2这四条线段满足的数量关系,并说明你得出此结论的理由.
【分析】(1) Rt△ABC中,已知AB=10,AC=6,可由勾股定理直接求出BC=8.不难发现连接AN可证AN=BN,在Rt△ACN中已知AC及AN与CN的数量关系,可设BN=x,则CN=8-x,由勾股定理得到方程62+(8-x)2=x2即能解出BN.
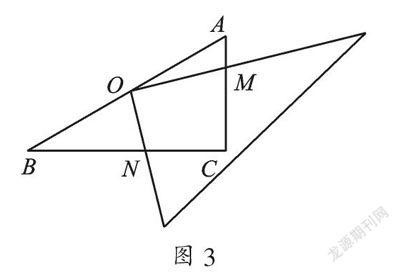
(2) 观察题中线段都含有平方,联想到勾股定理,但发现不能直接得出数量关系,只能添加辅助线构造全等将BN转化为AE,使得AM、AE和CM、CN存在两个直角三角形中,利用勾股定理则有AE2+AM2=EM2、CN2+CM2=MN2的数量关系,再由EM、NM相等建立等量关系便能解决问题.
解:(1) 连接AN.
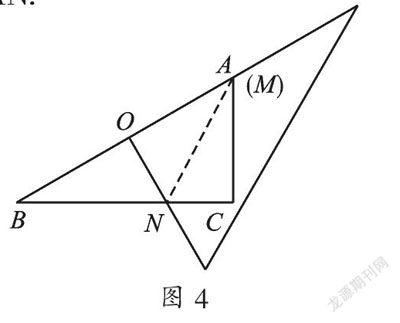
∵Rt△ABC中,∠C=90°,∴BC2=AB2-AC2=64,
∵BC>0,
∴BC=8,
∵OA=OB,
∠AON=∠BON,ON=ON,
∴△OAN≌△OBN(SAS),∴AN=NB.
设BN=x,则CN=8-x.
∵Rt△ACN中,∠C=90°,
∴AC2+CN2=AN2,∴62+(8-x)2=x2,
(2) 延长NO到E,使EO=NO,连接AE、EM、MN.
∵OB=OA,
∠NOB=∠EOA,ON=OE,
∴△NOB≌△EOA(SAS),
∴BN=AE,∠B=∠EAO,∴AE∥BC,
∴∠EAC+∠C=180°.
∵∠C=90°,∴∠EAC=90°,
∵MO垂直平分EN,∴EM=MN.
∵AE2+AM2=EM2,CN2+CM2=MN2,
∴AM2+BN2=CN2+CM2.
【点评】我们发现“方程”是解决勾股定理计算问题的有效工具,思路清晰,解题简便.我们也体会到直角三角形与等腰三角形有着密切的联系,把研究等腰三角形转化为研究直角三角形,转化的思想是研究问题的一种策略.
三、 整体思想
例3 已知a、b、c分别是Rt△ABC的两条直角边和斜边,且a+b=14,c=10,则S△ABC=_______.
【分析】一般的想法,要求直角三角形的面积,先求出其两条直角边a、b,则S△ABC即可求出,但这样求a、b非常繁杂,甚至在现阶段不可能.如果注意到:S△ABC=ab,那么只要求出ab这一整体就可以了.

解:由a+b=14,两边平方得:a2+2ab+b2=196,所以ab=,
根据勾股定理,a2+b2=c2.
【点评】运用整体思想,有时可以直奔主题,少走弯路,使问题的解决更方便、快捷,在一定程度上,体现了解题者的目标意识.
(作者单位:江苏省常州市兰陵中学)
