巧选择，妙解题

□陈德前

巧选择，妙解题

□陈德前

在运用解直角三角形的知识解决问题时，要注意优选边角关系，具体方式可概括为以下口诀：有斜（斜边）用弦（正弦、余弦），无斜（斜边）用切（正切），宁乘毋除，避中（中间数据）取原（原始数据）.

例1（2015·聊城）湖南路大桥于今年5月1日竣工，为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度，在距桥塔AB底部50米的C处，测得桥塔顶部A的仰角为41.5°（如图1）.已知测量仪器CD的高度为1米，则桥塔AB的高度约为（）

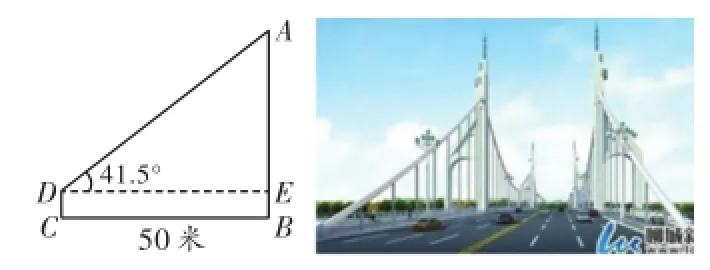
图1

A.34米 B.38米

C.45米 D.50米

分析：在Rt△ADE中，利用三角函数即可求得AE的长，则AB的长度即可求解.由于斜边未知，所以选用“无斜（斜边）用切（正切）”来求解.

解：过D作DE⊥AB于E，

∴DE＝BC＝50米.

在Rt△ADE中，

∴AE＝DE·tan41.5°

≈50×0.88＝44（米）.

∵CD＝1米，∴BE＝1米，

∴AB＝AE＋BE＝45（米）.

例2（2015·常德）图2是吊车在吊一物品时的示意图，已知吊车底盘CD的高度为2米，支架BC的长为4米，且与地面成30°角，吊绳AB与支架BC的夹角为80°，吊臂AC与地面成70°角，求吊车的吊臂顶端A点距地面的高度是多少米？（精确到0.1米）

（参考数据：sin10°＝cos80°＝0.17，cos10°＝sin80°＝0.98，sin20°＝cos70°＝0.34，tan70°＝2.75，sin70°＝0.94）

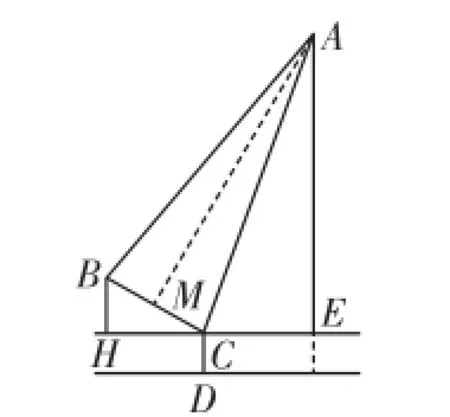
图2

分析：由题可知AB＝AC，然后利用解直角三角形的方法求出AC，为此作AM⊥BC于点M，可在Rt△ACM中求斜边AC，根据“有斜（斜边）用弦（正弦、余弦）”选用正弦或余弦；再在Rt△AEC中解出AE的长，同理选用正弦或余弦.

解：由题可知：如图2，BH⊥HE，AE⊥HE，CD＝2，BC＝4，∠BCH＝30°，∠ABC＝80°，∠ACE＝70°.

∴∠ACB＝80°.

∵∠ABC＝80°，

∴∠ABC＝∠ACB，

∴AC＝BC＝4.

过点A作AM⊥BC于M，

∴CM＝BM＝2.

∵在Rt△ACM中，CM＝2，∠ACB＝80°，

例3（广州）目前世界上最高的电视塔是广州新电视塔.如图3所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°.

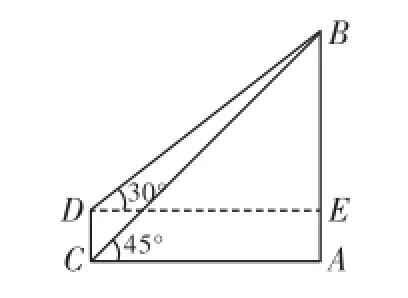
图3

（1）求大楼与电视塔之间的距离AC；

（2）求大楼的高度CD（精确到1米）.

分析：（1）由于△ABC是等腰直角三角形，所以AC＝AB.

（2）由矩形的性质可知DE＝AC＝610米，在Rt△BDE中可求出BE的长，用AB的长减去BE的长度即可.

解：（1）因为∠ACB＝45°，∠A＝90°，因此△ABC是等腰直角三角形，由题意，AC＝AB＝610（米）.

（2）DE＝AC＝610（米），

在Rt△BDE中，

故BE＝DE·tan39°.

因为CD＝AE，

所以CD＝AB－DE·tan39°＝610－610×tan39°

≈116（米）.