一个相似模型的诞生与应用

□王锋

一个相似模型的诞生与应用

□王锋

数学课程标准“要求学生能从较复杂的几何图形中分解提炼出基本图形，并掌握图形的基本特征，从而进一步分析其中的基本元素及其关系”.近几年的数学中考试卷中，就经常出现一些体现上述要求的试题.

引例（2015·德州）

（1）问题

如图1-1，在四边形ABCD中，点P为AB上的一点，∠DPC＝∠A＝∠B＝90°，求证：AD·BC＝AP·BP.

图1-1

图1-2

（2）探究

如图1-2，在四边形ABCD中，点P为AB上的一点，∠DPC＝∠A＝∠B＝θ时，上述结论是否依然成立？说明理由.

解析：（1）∵∠A＝∠CPD＝90°，

∴∠APD＋∠ADP

＝∠APD＋∠BPC＝90°，

∴∠ADP＝∠BPC.

又∠A＝∠B＝90°，

∴△APD∽△BCP.

∴AD·BC＝AP·BP.

（2）如果我们仍然能够证明△APD∽△BCP，则可猜想结论AD· BC＝AP·BP仍成立.

不妨类比（1）中的思路尝试探究.

说明：∵∠DPC＝∠A＝θ，

∠APD＋∠PDA

＝∠APD＋∠CPB＝180°－θ，

∴∠ADP＝∠BPC.

又∠A＝∠B＝θ，

∴△APD∽△BCP.

∴AD·BC＝AP·BP.

点评：本题以“问题——探究”方式设置了一个由“特殊到一般”的数学拓展问题.首先让同学们探索当等角为90°时，两个三角形相似，进而得到等积式（比例线段）的情形，然后拓广到等角为任意角情形下，探究原来结论成立的理由，实际上是特殊情形下思维的强化与正向迁移.

事实上上述问题中蕴含了一个非常重要的相似模型.为了我们以后在解题时运用其基本性质，可以根据图形本质特性，抽象出图2的相似模型.

模型发现通过探索猜想与推理证明，我们可以发现：

如图2，如果B、P、C在同一直线上，且∠B＝∠EPF＝∠C，那么△BPE∽△CFP.否则相似关系不成立.

图2

为了应用的方便，我们根据图形的特征结构不妨把它命名为“一线三等角型”相似模型.

模型应用上述相似的数学模型就是命题专家匠心独运、勇于创新、精心培育驯养的一匹“黑马”.如果我们能够在复杂的图形中，慧眼观察发现其中隐藏的上述基本图形，联想其相似的性质，就能让我们在相似的“沙场”上，披荆斩棘，战功卓著.

例1（2015·泰安）如图3，在△ABC中，AB＝AC，点P、D分别是BC、AC边上的点，且∠APD＝∠B.

（1）求证：AC·CD＝CP·BP；

（2）若AB＝10，BC＝12，当PD∥AB时，求BP的长.

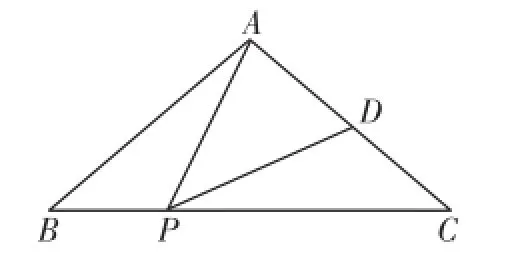
图3

解析：（1）在△ABC中，

∵AB＝AC，∴∠C＝∠B.

又∠APD＝∠B，

∴∠B＝∠APD＝∠C.

根据相似模型可证得

△ABP∽△PCD，

即AC·CD＝PC·BP.

（2）∵PD∥AB，

∴∠BAP＝∠APD.

又∠APD＝∠B＝∠C，

∴∠BAP＝∠C，

∴△BAP∽△BCA，

又AB＝10，BC＝12，

点评：（1）本题以等腰三角形为载体，设计了一个“一线三等角型”相似模型的常见基本图形.

（2）本题的另一特色在于抓住了相似形中常见的基本图形——共边（AB），共角（∠B）的一对相似形△BAP∽△BCA.

上述两个基本相似模型的应用务必引起同学们的高度重视.

例2（2015·孝感）如图4，△AOB是直角三角形，∠AOB＝90°，OB＝ 2OA，点A在反比例函数的图象上.若点B在反比例函数的图象上，求k的值.

图4

易证△BDO∽△OCA，

若设点A的坐标为（a，b），

则BD＝2a，OD＝2b，

B点的坐标是（－2b，2a）.

故k＝－2b·2a＝－4a·b＝－4.

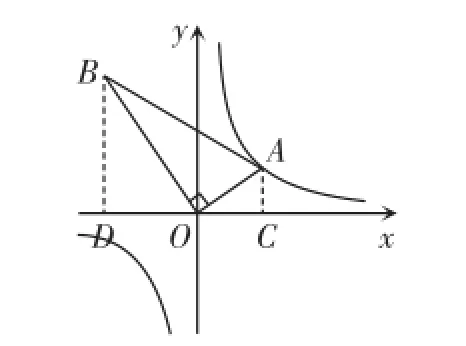
图5

点评：确定反比例函数的解析式，一般只要知道其图象上一个点的坐标，便可确定比例系数k，而反比例函数的图象经过点B，则须要确定点B坐标.为了探究点B的坐标，我们根据图形的结构特征，通过作两条垂线，构造出了“一线三等角”的基本相似模型，然后根据相似三角形的性质——对应边成比例，将点B、A两点的坐标紧密地联系在一起，为顺利获取k值起到了关键的作用.