拉杆倾角对斜拉桥桥塔侧向稳定性的影响

薛 江，李自林,2，邢 颖，丁宏毅

拉杆倾角对斜拉桥桥塔侧向稳定性的影响

薛 江1，李自林1,2，邢 颖1，丁宏毅1

(1. 天津大学建筑工程学院，天津 300072；2. 天津城建大学土木工程学院，天津 300384)

针对刚性拉杆斜拉桥拉杆倾角对桥塔侧向稳定性影响的问题，基于能量原理，以单承重面刚性拉杆斜拉桥为研究对象，推导出带有刚性拉杆考虑扭转变形的斜拉桥侧向弹性稳定系数解析计算公式并以算例进行验证，研究了辐射式、竖琴式和扇形3种不同索面类型斜拉桥拉杆倾角对桥塔侧向弹性稳定性的影响．结果表明：拉杆倾角与桥塔侧向稳定性系数存在非线性关系，不同类型索面斜拉杆倾角变化对桥塔稳定性系数“非保向力”效应的影响均是不同的．

斜拉桥；刚性拉杆；非保向力；拉杆倾角；弹性稳定系数

斜拉桥是一种桥面体系受压、支撑体系受拉的桥梁，梁塔是主要的承重构件，借助斜拉索组合成整体结构[1]．对于斜拉桥的桥塔结构除了承受本身的自重引起轴力之外，还承受通过斜拉索传递给塔身的主梁桥面系的重力，以及主梁桥面系所承受的竖向荷载和水平荷载．因而，桥塔结构在强大轴向压力作用下的稳定性问题，日益受到人们的重视．由于结构体系的特点，桥塔纵向失稳的可能性较小，因而其稳定性研究主要限于桥塔横向失稳[2]．对于斜拉桥稳定性分析，国内外学者在空气动力稳定性和空气静力稳定性两方面做了大量的研究[3-8]；而针对斜拉桥桥塔侧向稳定性的研究目前大多是关于桥塔稳定性计算方法的研究，如葛耀君[9]用能量变分方法导出了索、塔与梁耦合作用下的单索面斜拉桥侧倾稳定的计算公式，建立了由拉索、桥塔和主梁所组成的斜拉桥系统的稳定分析实用计算方法；罗晓峰[10]以卡罗波夫折减法为基础，提出了一种改进的计算斜拉桥桥塔稳定系数的方法——修正的弹性支承法；香港大学的Xi等[11]提出了一种计算斜拉桥面内极限承载能力的能量分析法，该方法使用简单，具有较高的收敛速度；肖汝成[12]以单承重面桥梁结构为研究对象，考虑拉索与吊杆的“非保向力系”效应，用能量法推导适用于工程计算的单承重面结构横向稳定的临界荷载计算公式．此外还有关于桥塔空气动力稳定性的研究，如Michaltsos等[13]研究了在由于桥面振动产生的时变荷载作用下斜拉桥桥塔的稳定性问题；Wang等[14]对单索面斜拉桥的颤振稳定性进行分析．对于斜拉桥桥塔的侧向稳定性问题的研究离不开“非保向力”效应，目前的研究大多是关注于柔性拉索拉力的“非保向力”效应，但却忽视了刚性拉杆抗扭刚度带来的“非保向力”效应，这对斜拉桥的分析和设计来说是一种缺失，因此需要通过对刚性拉杆(刚性拉杆是指预应力钢筋混凝土斜拉杆，一般为矩形截面；相对常见采用钢索作为斜拉索的斜拉桥来说，刚性拉杆的截面面积是其十几倍，抗弯刚度和扭转刚度大许多，垂度较小，例如秦皇岛市大里营铁路斜拉桥)抗扭刚度带来的“非保向力”效应进行分析研究，来进一步完善斜拉桥“非保向力”效应理论．

笔者首先根据能量原理推导了计入刚性拉杆抗扭刚度和拉杆拉力的单索面斜拉桥桥塔弹性稳定系数计算公式，然后对一座单索面刚性拉杆斜拉桥分别采用放射形、竖琴形和扇形3种形式布置拉索计算其桥塔侧向弹性稳定系数，并通过分别改变各形式拉索倾斜的角度来分析拉索倾角的变化对桥塔侧向弹性稳定安全系数的影响．考虑斜拉杆抗扭刚度对桥塔稳定性影响的研究方法和研究成果推广应用到多数的斜拉桥中，可以使得其稳定性计算结果更为合理，能够为多数斜拉桥桥塔稳定性的理论研究和施工提供重要的依据．平面，会造成梁、杆与塔不再位于同一平面，拉杆传递的荷载方向是在不断改变的，但始终指向桥面纵轴线(如图2所示)，进而对桥塔的侧向稳定性产生影响；同时由于桥塔斜拉杆锚固点的位移会使斜拉杆产生扭转，也会对桥塔的侧向稳定性产生影响，因此这2个由斜拉杆产生的影响共同作用于桥塔，相当于在其拉杆锚固点上都增加了一个横向弹性支撑(如图3所示)．这样，在斜拉桥桥塔失稳时，桥塔弯曲会产生弯曲势能，横向弹性支撑发生变形产生应变能(即斜拉杆对桥塔侧向失稳具有“非保向力”效应)，桥塔

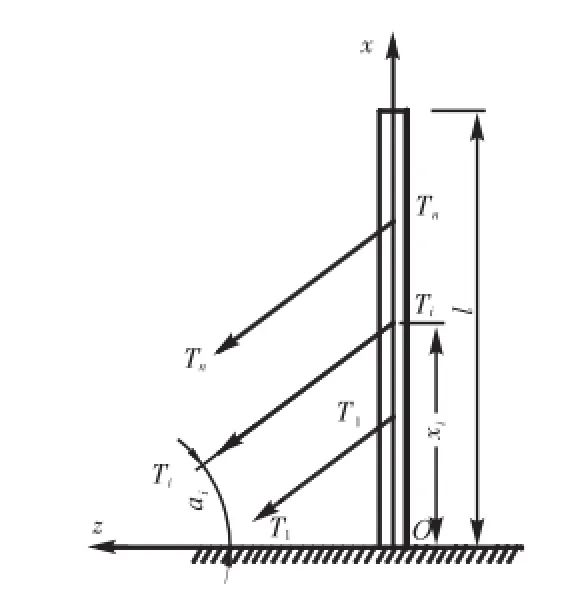
图1 桥塔纵桥向示意Fig.1 Schematic diagram of vertical of pylon

1 刚性拉杆斜拉桥桥塔的侧倾稳定系数计算

1.1 理论假设

对研究问题采用能量法进行分析，计算时主梁采用小变形理论，因此进行以下假设：

(1) 主梁有可靠的横向联系，即主梁在横向变形时相对塔而言有无穷大的横向刚度．

(2) 斜拉杆变形前后长度不发生变化，斜拉杆在变形后与主梁的水平夹角变化微小，即斜拉杆在变形后与主梁的水平夹角不变．

(3) 塔墩固结处及拉杆与梁体锚固处无水平位移．

1.2 计算力学模型的简化分析

根据假设条件，桥塔就转换为一端固定、一端自由的悬臂柱(如图1所示)．桥塔失稳前，梁杆与塔位于同一平面内；当桥塔侧向失稳时，桥塔将鼓出塔索弯曲会使其在自重作用下做功，桥塔变形使得桥塔拉杆锚固点发生位移会使斜拉杆拉力做功．

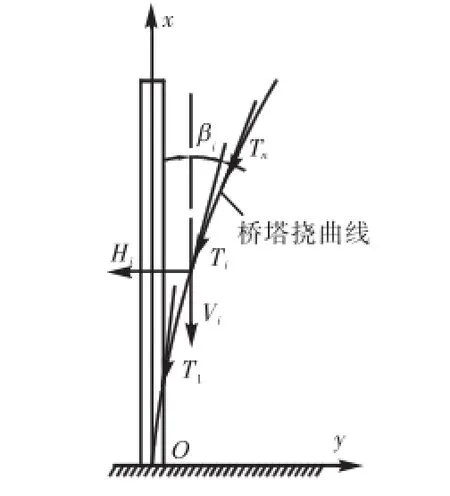
图2 桥塔侧向失稳示意Fig.2 Schematic diagram of lateral instability of pylon

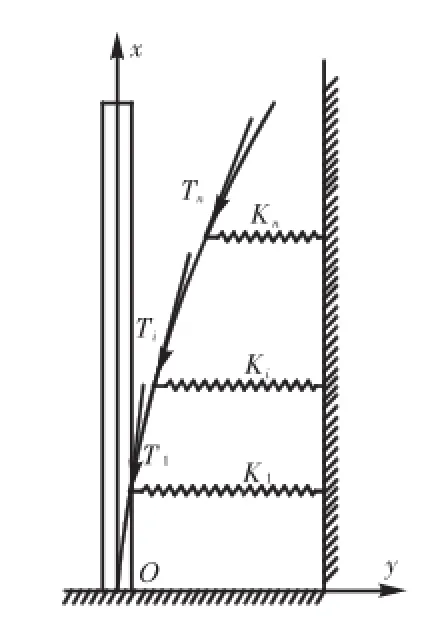
图3 弹性支撑示意Fig.3 Schematic diagram of elastic support

1.3 桥塔横向弹性稳定系数计算公式推导

把桥塔作为研究对象，作用于桥塔的外力有桥塔本身的自重及斜拉杆的拉力，各拉杆拉力Ti(i=1，2，3，4，…，n)与梁体的水平夹角为αi．

桥塔侧向失稳时，刚性拉杆扭转角度方程为

式中：θi为第i根斜拉杆的扭转角度；lix为第i根拉杆的长度．

设桥塔的挠曲线方程为

以上两个曲线方程在边界上必须满足位移边界条件，斜拉杆坐标如图4所示．

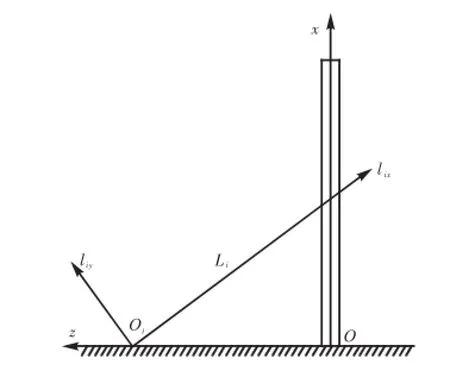
图4 拉杆坐标示意Fig.4 Schematic diagram of coordinate of pull rod

斜拉杆拉力对桥塔的作用力可分解为平行于塔杆平面的竖向力Vi和垂直于塔杆平面的水平力Hi(如图2所示)，可表示为

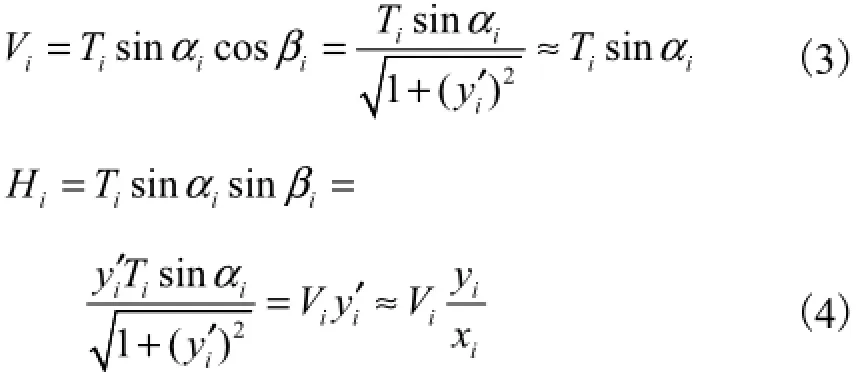
桥塔的应变能UE为

式中：pE、pI分别为桥塔的抗弯刚度；l为桥塔高度．

横向弹性支撑应变能kU包括桥塔失稳时，斜拉杆拉力弹性支撑效应产生的弹簧应变能′和刚性斜拉杆扭曲时产生的扭转应变能Uφ，即

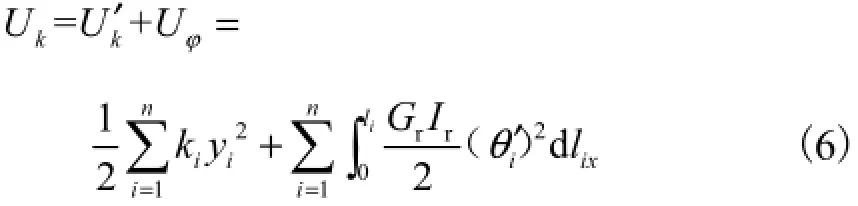
式中：Uk为横向弹性支撑应变能；Gr、Ir分别为拉杆的抗扭刚度，均为常数；n为斜拉杆根数；li为第i根斜拉杆杆长；ki为第i根斜拉杆水平分量的虚拟弹簧系数，由式(4)得

即得

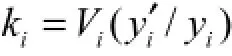
桥塔自重的外力势能Vg为

斜拉杆分量ViV的外力势能

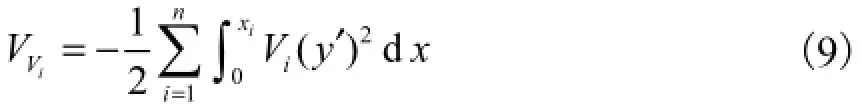
式中：q为桥塔单位长度；xi为桥塔轴线与第i根斜拉杆轴线相交处的坐标．

根据斜拉桥桥塔的边界条件，设

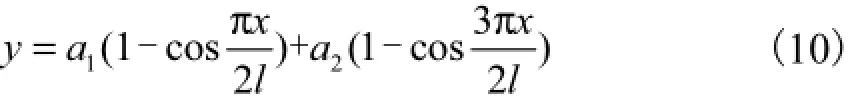
式(10)满足位移边界条件．

假设刚性斜拉杆的扭转变形为线性的．设(xi1，yi1)为第i根拉杆桥塔锚固处上表面轴线端点坐标，(xi2，yi2)为第i根斜拉杆桥塔锚固处下表面轴线端点坐标(如图5所示)；根据计算力学模型假设条件(1)和(2)，刚性斜拉杆扭转角度方程可表示为

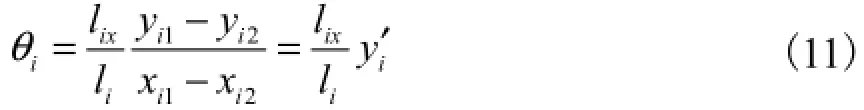
将式(10)、式(11)代入式(5)～式(9)，通过推导计算，得到

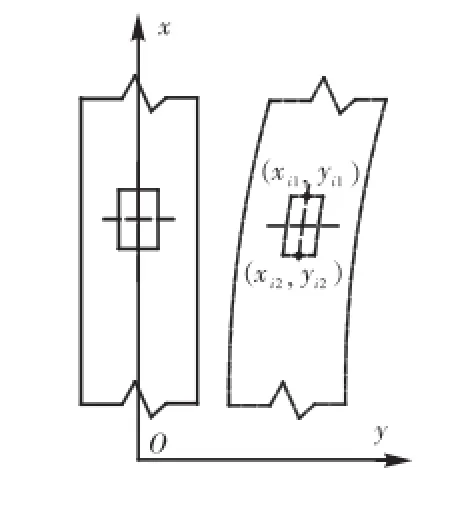
图5 斜拉杆与桥塔锚固处坐标示意Fig.5Schematic diagram of coordinate of rod-to-pylon anchor

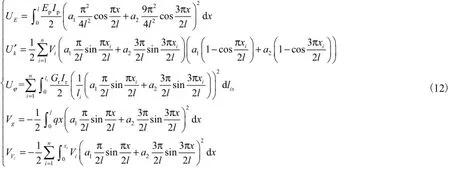
设桥塔失稳时桥塔失稳的弹性稳定系数为λ，则在临界荷载作用时总势能为

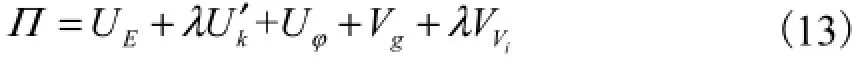
利用能量驻值原理

将式(12)和式(13)代入式(14)，经计算可得

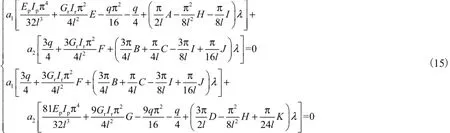
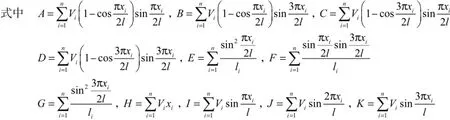
要使方程组中的1a、2a具有非零解，其系数行列式等于零，可以得到特征方程，即

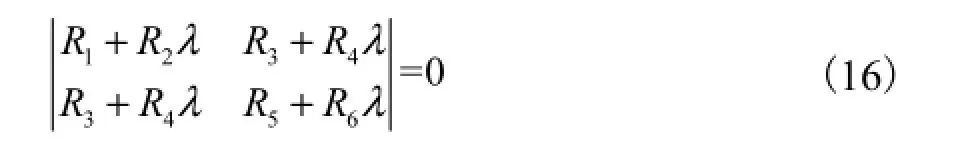
式中

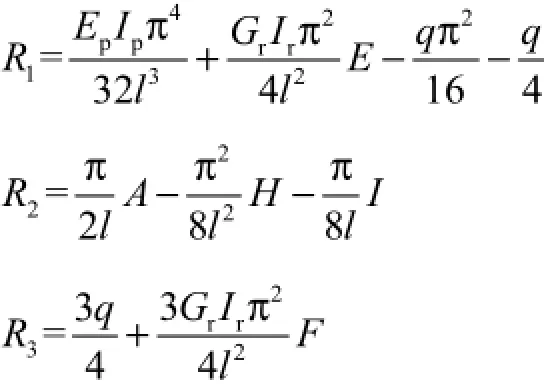
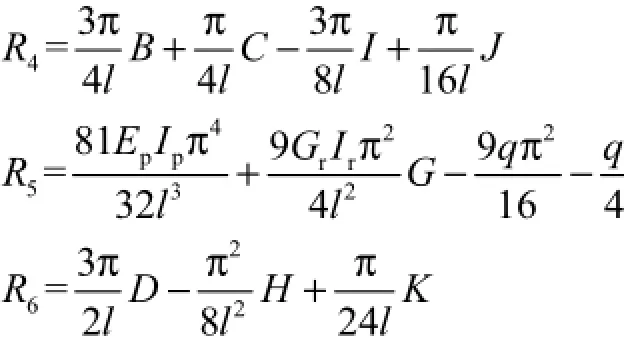
求解式(16)，可得

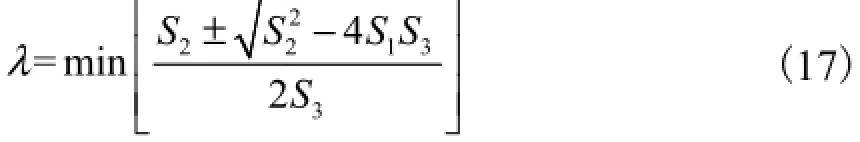
式中

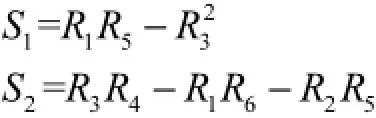
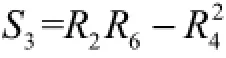
2 算例分析

2.1 算例及计算

某刚性拉杆斜拉桥为预应力混凝土独塔两跨斜拉桥，(见图6)．主跨布置为72,m+72,m，桥梁全长为144,m，采用单塔双索面预应力斜拉索结构，桥塔高47.3,m，桥塔截面尺寸1.5,m×3,m，桥塔两侧各设8根斜拉杆，拉杆成竖琴式布置，斜拉杆为预应力混凝土刚性拉杆，该桥具体的尺寸参数见表1～表3．

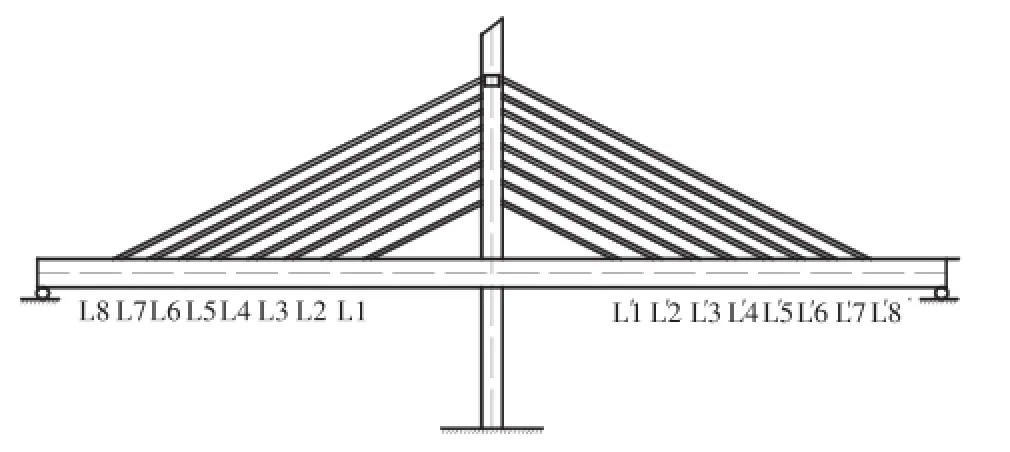
图6 斜拉桥示意Fig.6 Schematic diagram of cable-stayed bridge

表1 桥塔参数Tab.1 Parameters of pylon

表2 斜拉杆材料参数Tab.2 Parameters of tension diagonal material

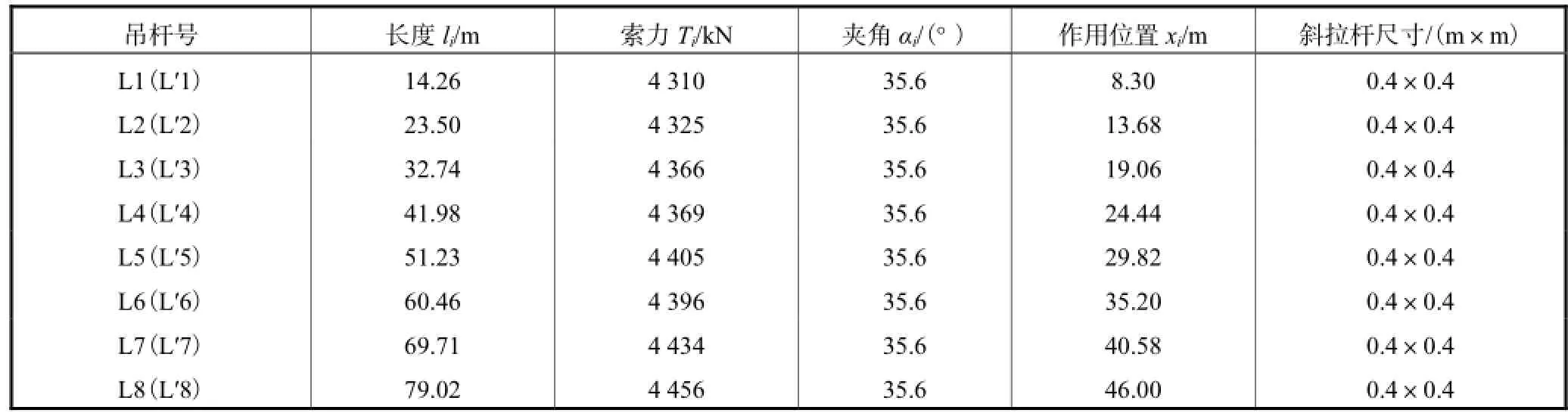
表3 斜拉杆数值Tab.3 Numerical values of tension diagonal

将上述数值代入式(17)可以得该桥塔的侧向弹性稳定系数为λ1=17.63．

如果在计入“非保向力”作用时，不考虑刚性斜拉杆的抗扭刚度，则该桥塔的侧向弹性稳定系数为λ2=17.58．

如果不计入“非保向力”作用，则该桥塔的侧向弹性稳定系数为λ3=6.66．

对比上述3个桥塔面外稳定系数可得稳定系数比值n为

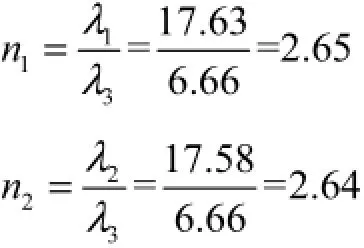
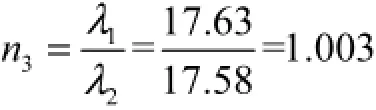
2.2 算例结果分析

经过对该桥的几个稳定性系数进行计算可以知道：

(1) 对于该桥，考虑拉杆“非保向力”效应计算的稳定性系数是不考虑的2.64(或2.65)倍；

(2) 当考虑拉杆的“非保向力”效应时，计入拉杆扭转的稳定性系数与不计入的稳定性系数提高0.3%．

3 影响桥塔侧向稳定系数的参数分析

通过刚性拉杆斜拉桥桥塔的侧向弹性稳定系数公式的推导，可以看出斜拉杆倾角对弹性稳定系数有影响，因此以上述算例中斜拉桥的尺寸为基本参数，选取3种不同的斜拉杆布置形式讨论斜拉杆倾角对桥塔侧向弹性稳定性的影响．选取的斜拉杆布置形式分别为辐射式索面、竖琴式索面和扇形索面．

3.1 辐射式索面

将算例中的斜拉杆采用辐射式布置(见图7)，主梁上拉杆锚固位置采用算例提供的位置，桥塔上拉杆采用等间距布置，间距d=0.5,m；最外侧斜拉杆的倾角为α．在合理的范围内改变最外侧拉杆倾角αout，其他参数不变，可以得到辐射式斜拉桥最外侧拉杆倾角αout与桥塔侧向稳定系数λ的关系．图8(a)为最外侧斜拉杆倾角αout与桥塔弹性稳定系数λ1、λ2和λ3的关系，图8(b)为最外侧斜拉杆倾角αout与桥塔弹性稳定系数比值n1和n2的关系，图8(c)为最外侧斜拉杆倾角αout与桥塔弹性稳定系数比值n3的关系．

对辐射式斜拉杆斜拉桥桥塔侧向稳定系数计算结果进行分析可知：

(1) 对于辐射式索面斜拉桥，考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2，随着最外侧拉杆倾角αout的增大而增大；不考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ3，则随着最外侧拉杆倾角αout的增大而减小，但变化很微小．

(2) 对于辐射式索面斜拉桥，考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2与最外侧拉杆倾角αout呈非线性关系；当28.6°＜αout＜32.5°时，考虑斜拉杆的“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2迅速增加；当32.5°＜αout＜36.2°时，考虑斜拉杆的“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2增加缓慢，斜拉杆的“非保向力”效应对桥塔稳定性的提高幅度有限．

(3) 对于辐射式索面斜拉桥，考虑斜拉杆“非保向力”效应时，桥塔侧向稳定系数比值n3，随着最外侧拉杆倾角αout的增大而减小，并逐渐趋于1．

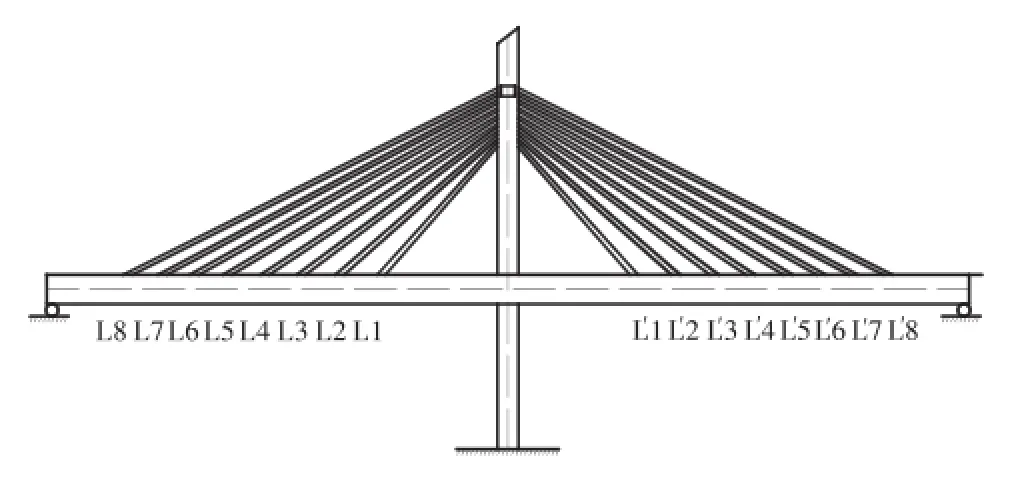
图7 辐射式索面斜拉桥示意Fig.7 Schematic diagram of cable-stayed bridge with radiation-type cable plane

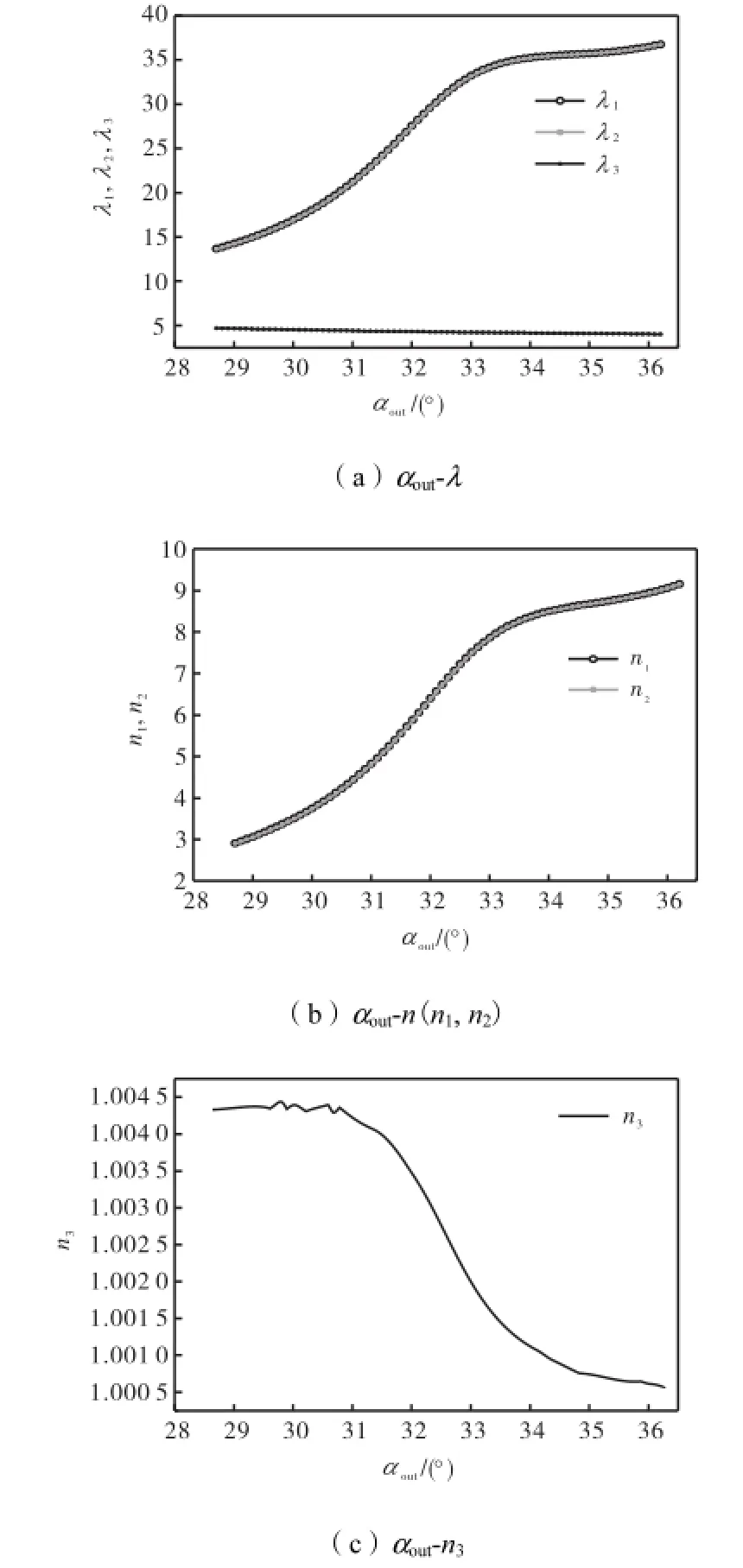
图8 辐射式索面斜拉桥斜拉杆倾角对桥塔稳定性的影响Fig.8Influence of rigid rod angle on stability of cablestayed bridge pylon with radiation-type cable plane

3.2 竖琴式索面

将算例中的斜拉杆采用竖琴式布置(见图9)，主梁上拉杆锚固位置采用算例提供的位置，所有斜拉杆的倾角角度均为α．在合理的范围内改变斜拉杆拉杆倾角α，其他参数不变，可以得到竖琴式斜拉桥斜拉杆倾角α与桥塔侧向稳定系数λ 的关系．图10(a)为斜拉杆倾角α 与桥塔弹性稳定系数λ1、λ2和λ3的关系，图10(b)为斜拉杆倾角α与桥塔弹性稳定系数比值n1和n2的关系，图10(c)为斜拉杆倾角α与桥塔弹性稳定系数比值n3的关系．

对竖琴式斜拉杆斜拉桥桥塔侧向稳定系数计算结果进行分析可知：

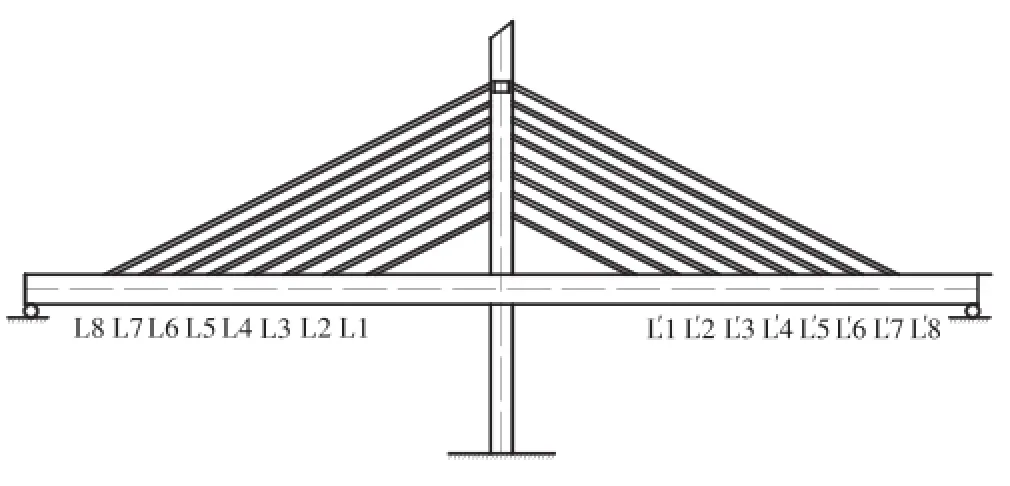
图9 竖琴式索面斜拉桥示意Fig.9 Schematic diagram of cable-stayed bridge with harp-type cable plane

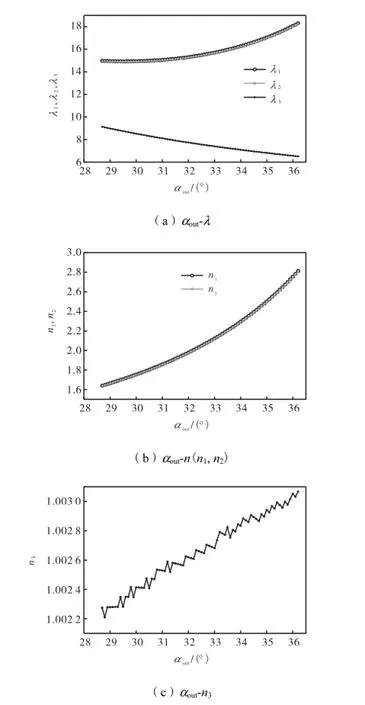
图10 竖琴式索面斜拉桥斜拉杆倾角对桥塔稳定性的影响Fig.10 Influence of rigid rod angle on of cable-stayed bridge pylon with harp-type cable-plane

(1) 对于竖琴式索面斜拉桥，考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2与斜拉杆倾角α 呈非线性关系，并随其增大而增大，当28.6°＜α＜31.5°时，λ1和λ2增长缓慢，当31.5°＜α＜36.2°时，λ1和λ2增长迅速；不考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ3与斜拉杆倾角α 基本呈非线性关系，随其增大而减小，整体减小趋势一致.

(2) 对于竖琴式索面斜拉桥，桥塔侧向弹性稳定系数比值n1和n2与斜拉杆倾角α 呈非线性关系，随着斜拉杆倾角α 的增大而不断增大，增长趋势比较明显．

(3) 对于竖琴式索面斜拉桥，考虑斜拉杆“非保向力”效应时，桥塔侧向稳定系数比值n3与斜拉杆倾角α 近似呈线性关系，并随其增大而增大．

3.3 扇形索面

将算例中的斜拉杆采用扇形布置(见图11)，主梁上拉杆锚固位置采用算例提供的位置，桥塔上拉杆锚固点采用等间距布置，间距为d．在合理的范围内通过改变桥塔上拉杆锚固点间距d来改变各斜拉杆倾角值αi，其他参数不变，可以得到扇形斜拉桥桥塔拉杆锚固点间距d与桥塔侧向稳定系数λ的关系．图12(a)为桥塔拉杆锚固点间距d与桥塔弹性稳定系数λ1、λ2和λ3的关系，图12(b)为桥塔拉杆锚固点间距d与桥塔弹性稳定系数比值n1和n2的关系，图12(c)为桥塔拉杆锚固点间距d与桥塔弹性稳定系数比值n3的关系．

对扇形索面斜拉桥桥塔侧向稳定系数计算结果进行分析可知：

(1) 对于扇形索面斜拉桥，考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2与桥塔拉杆锚固点间距d呈非线性关系；当0.5,m＜d＜1.5,m时，λ1和λ2略有变化；当1.5,m＜d＜6.6,m时，λ1和λ2呈凹曲线变化，其中当1.5,m＜d＜4.4,m时，λ1和λ2随d增加而减小，当4.4,m＜d＜6.6,m时，λ1和λ2随d增加而增大．未考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ3与桥塔拉杆锚固点间距d呈非线性关系，随着d的增加而增加，但增加趋势较小．

(2) 对于扇形索面斜拉桥，桥塔侧向弹性稳定系数比值n1和n2与桥塔拉杆锚固点间距d呈非线性关系，变化趋势与考虑斜拉杆“非保向力”效应的桥塔侧向弹性稳定系数λ1和λ2变化趋势一致．当0.5,m＜d＜1.5,m时，n1和n2略有变化；当1.5,m＜d＜6.6,m时，n1和n2呈凸形抛物线变化，其中当1.5,m＜d＜4.4,m时，n1和n2随d增加而减小，当4.4,m＜d＜6.6,m时，n1和n2随d增加而增大．

(3) 对于扇形索面斜拉桥，考虑斜拉杆“非保向力”效应时，桥塔侧向稳定系数比值n3与桥塔拉杆锚固点间距d呈非线性关系，随着d的增大n3表现为凸曲线线变化．当0.5,m＜d＜1.2,m时，n3随着d的增大而增大，增大趋势很小；当1.2,m＜d＜3.2,m时，n3随着d的增大而迅速增大，增加趋势很明显；当3.2,m＜d＜6.6,m时，n3随着d的增大而逐渐减小．

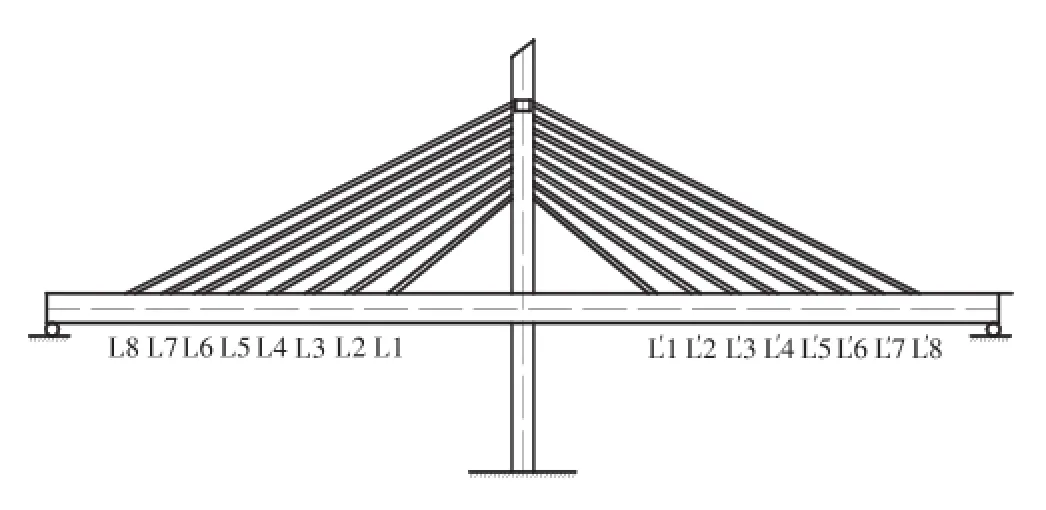
图11 扇形索面斜拉桥示意Fig.11 Schematic diagram of cable-stayed bridge with sector-type cable plane

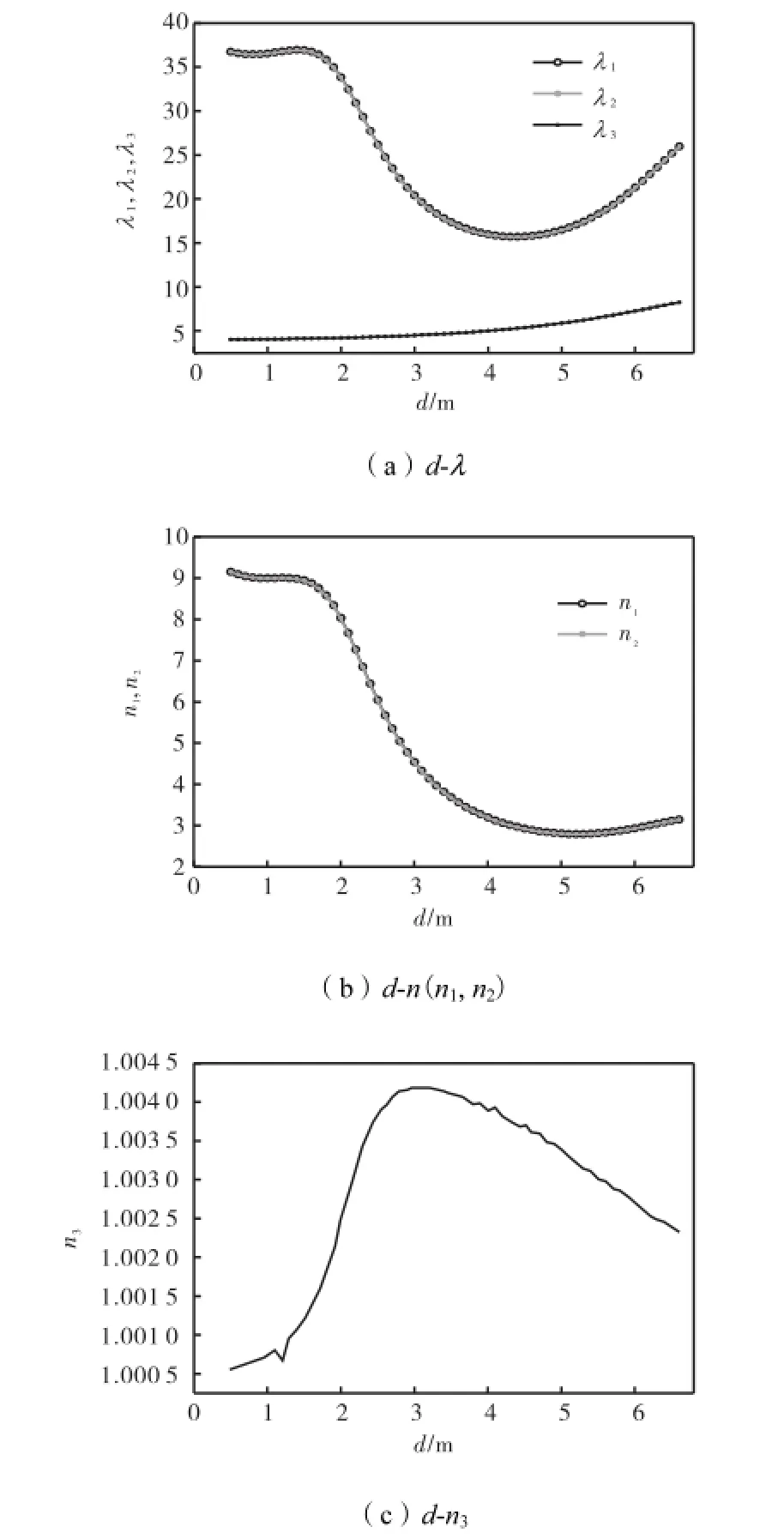
图12 扇形索面斜拉桥桥塔拉杆锚固点间距对桥塔稳定性的影响Fig.12 Influence of anchorage-point distance which is in pylon on stability of cable-stayed bridge pylon with sector-type cable plane

4 结 论

通过对辐射式、竖琴式和扇形3种索面刚性拉杆斜拉桥的稳定性分别从共同考虑拉杆扭转和拉力的“非保向力”作用、仅考虑拉杆拉力的“非保向力”作用和不考虑拉杆“非保向力”作用等3方面进行讨论分析后，可以得到刚性拉杆斜拉桥索面布置形式对桥塔稳定性的影响．

(1) 对于刚性拉杆斜拉桥，斜拉杆倾角对桥塔的侧向弹性稳定系数是有影响的．在考虑斜拉杆的“非保向力”效应时，对于辐射式索面斜拉桥，随着斜拉杆倾角增大，其计算出来的弹性稳定系数会增大并趋于稳定，拉杆倾角对桥塔侧向弹性稳定性的影响有限；对于竖琴式索面斜拉桥，随着斜拉杆倾角增大，其计算出来的弹性稳定系数会增大，同时也对桥塔的侧向稳定性也越有利．

(2) 考虑斜拉杆的“非保向力”效应时，对于弹性稳定系数增长趋势来说，当斜拉杆同样的变化趋势时，辐射式索面斜拉桥要比竖琴式斜拉桥增长的更快更明显；当拉杆倾角小于31°时，两者的桥塔侧向弹性稳定系数相差不大，当拉杆倾角大于31°时，且前者计算出来的稳定系数较后者更大．因此在斜拉桥索面设计时，应当予以考虑．

(3) 考虑斜拉杆的“非保向力”效应时，对于辐射式索面斜拉桥，桥塔侧向弹性稳定系数比值n3，随拉杆倾角的增大而减小；对于竖琴式索面斜拉桥，桥塔侧向弹性稳定系数比值n3，随拉杆倾角的增大而增大．

(4) 未考虑斜拉杆的“非保向力”效应时，辐射式索面斜拉桥计算出来的弹性稳定系数基本上随拉杆倾角的变化不大，而对于竖琴式索面斜拉桥，其计算出来的弹性稳定系数却是随着拉杆倾角的增大而明显减小．因此在采用辐射式索面或竖琴式索面作为斜拉桥设计索面时，上述现象应该予以考虑．

(5) 对于扇形索面斜拉桥，考虑斜拉杆的“非保向力”效应时，随着桥塔拉杆锚固点间距的增大，其桥塔侧向弹性稳定系数呈凹曲线变化，存在峰值；桥塔侧向弹性稳定系数比值n3，随着桥塔拉杆锚固点间距的增大呈凸曲线变化，也存在峰值．在扇形索面斜拉桥设计时，应当予以考虑．

(6) 对于扇形索面斜拉桥，斜拉杆的“非保向力”效应所增加的桥塔侧向弹性稳定系数，随着桥塔拉杆锚固点间距的增大而减小．未考虑斜拉杆的“非保向力”效应时，其桥塔侧向弹性稳定系数随着桥塔拉杆锚固点间距的增大而增大．

(7) 通过3种索面桥塔稳定性的对比，建议选择竖琴式索面作为斜拉桥拉索布置形式．当不考虑拉杆“非保向力”效应时，竖琴式索面桥塔稳定性系数变化的平均值较其他两种要高，λ3在6.5～9.3之间变化，扇形索面的λ3在5.0～4.0之间变化，辐射式索面的λ3在8.3～4.0之间变化；从考虑拉杆“非保向力”效应的桥塔稳定性系数与不考虑的桥塔稳定性系数比值n1和n2来说，竖琴式索面的变化范围小，且变化趋势唯一．

［1］ 林元培. 斜拉桥[M]. 北京：人民交通出版社，2004.

Lin Yuanpei. Cable-Steyed Bridge[M]. Beijing：The People’s Communication Publishing House，2004(in Chinese).

［2］ 项海帆. 高等桥梁结构理论[M]. 北京：人民交通出版社，2010.

Xiang Haifan. Advanced Theory of Bridge Structures [M]. Beijing：The People’s Communication Publishing House，2010(in Chinese).

［3］ Kim M-Y，Lee J-S，Kyung Y-S. System stability design of cable-stayed bridges based on elastic/inelastic system buckling analyses[C]//4,th International Conference on Bridge Maintenance．Seoul，Korea，2008：249-250.

［4］ Choi Dong-Ho，Yoo Hoon，Koh Jung-Hoon，et al．Stability evaluation of steel cable-stayed bridges by elastic and inelastic buckling analyses[J]. International Journal of Structural Stability and Dynamics，2007，7(4)：669-691.

［5］ Katsuch Hiroshi，Yamada Hitoshi，Ohashi Harukazu. A study on aerodynamic characteristics of edge-girder deck of composite cable-stayed bridge[J]. Journal of Wind Engineering，2009，34(4)：103-110.

［6］ Vairo Giuseppe. A simple analytical approach to the aeroelastic stability problem of long-span cable-stayed bridges[J]. International Journal of Computational Methods in Engineering Science and Mechanics，2010，11(1)：1-19.

［7］ Kao Chin-Sheng，Kou Chang-Huan，Xie Xu. Static instability analysis of long-span cable-stayed bridges with carbon fiber composite cable under wind load[J]. Tamkang Journal of Science and Engineering，2006，9(2)：89-95.

［8］ Zhang Xinjun，Sun Bingnan，Xiang Haifan. Aerodynamic stability of cable-stayed bridges under erection[J]. Journal of Zhejiang University Science，2005，6A (3)：175-180.

［9］ 葛耀君. 索-塔-梁耦合作用下的斜拉桥侧倾稳定研究[J]. 中国公路学报，1995，8(4)：38-44.

Ge Yaojun. Researeh of latral buekling stability of cablestayed bridges under cable -pylon-girder coupling [J]. China Journal of Highway and Transport，1995，8(4)：38-44(in Chinese).

［10］ 罗晓峰. 斜拉桥桥塔稳定性实用计算方法[J]. 公路交通科技，2011，28(9)：61-65.

Luo Xiaofeng. A practical calculation method of stability for pylon of cable-stayed bridge [J]. Journal of Highway and Transportation Research and Development，2011，28(9)：61-65(in Chinese).

［11］ Xi Ying，Kuang J S. Ultimate load capacity of cablestayed bridges[J]. Journal of Bridge Engineering，1999，4(1)：14-22.

［12］ 肖汝成. 单承重面桥梁结构横向稳定的实用计算[J].华东公路，1990，64(3)：34-40.

Xiao Rucheng. A practical calculation method of lateral stability for bridge with single loading plane [J]. East China Highway，1990，64(3)：34-40(in Chinese).

［13］ Michaltsos G T，Raftoyiannis I G，Konstantakopoulos T G. Dynamic stability of cable-stayed bridge pylons [J]. International Journal of Structural Stability and Dynamics，2008，8(4)：627-643．

［14］ Wang Huili，Pan Zhe，Jiang Rongbin. Analysis of flutter stability of cable-stayed bridge with single cable plane[C]//2011 International Conference on Structures and Building Materials．Swityerland，2011：4320-4323.

Influence of Rigid Rod Angle on Lateral Stability of Cable-Stayed Bridge Pylon

Xue Jiang1，Li Zilin1,2，Xing Ying1，Ding Hongyi1
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Tianjin Chengjian University，Tianjin 300384，China)

To overcome the influence of rigid rod angle on the lateral stability of cable-stayed bridge pylon, the analytical formula for the lateral elastic stability coefficient of the cable-stayed bridge was derived with the torsional deformation of rigid rod considered and then verified by an example. The influence of rigid rod angle on the lateral stability of cable-stayed bridge pylon with three difference types of cable plane, which were radiation-type, harp-type and sector-type cable planes, was investigated. Results show that there exists a nonlinear relationship between rigid rod angle and the lateral buckling coefficient of pylon, and that the change in rigid rod angle of cable plane of different type has a different influence on the lateral stability of cable-stayed bridge pylon and nondirectional force.

cable-stayed bridge；rigid rod；nondirectional force；rigid rod angle；elastic stability coefficient

U441；TU311.2

A

0493-2137(2013)10-0901-09

DOI 10.11784/tdxb20131008

2012-10-12；

2013-02-22.

国家重点基础研究发展计划(973计划)资助项目(2011CB013603)；住房和城乡建设部软科学研究资助项目(2012-K4-28)．

薛 江（1985— ），男，博士研究生，xuejiang04@163.com.

李自林，hebeigaomuying@163.com.