压缩FP－Tree的改进搜索算法

吴 倩，罗健旭

（华东理工大学 信息学院，上海200237）

0 引 言

通过算法输出频繁项集是关联规则挖掘的核心步骤［1］。频繁项集挖掘大致可以分为两类：一类是基于候选项集产生－检验的Apriori类算法，如IAA［2］，RAAT［3］，IApriori［4］，这类算法从经典算法Apriori上演变而来，算法流程简单且易于理解，在候选项集得到约减时，算法效率会得到很大提高，但是算法需要多次扫描数据库以统计项集支持度，在数据库较大时，处理效率很低，在I／O 上消耗时间很多［5］；另一类算法是基于树形结构的模式增长类算法，如FP－Growth［6］、COFI－Tree［7］、CT－PRO［8］等，它们在挖掘过程中无候选频繁项集产生，且均基于分而治之的策略，对基于主树建立的子树进行挖掘，这类算法在数据库巨大时有效压缩了数据中的重要信息，使得搜索效率较Apriori类算法得到很大提高［9］。

本文结合两类算法的优点，采用模式增长类算法紧凑的树形数据结构，第一步，遍历原始数据库，找到满足最小支持数的所有频繁1项集，构建压缩频繁模式树 （CFPTree）；第二步，基于分而治之的策略，分别建立了局部压缩频繁模式树LocalCFP－Tree；第三步，利用Apriori算法的产生候选项集，自底向上遍历LocalCFP－Tree来统计其支持数，从而得到全部频繁模式。改进算法解决了Apriori算法因多次扫描数据库而耗时长的问题，也避免了模式增长类算法因大量递归调用出现内存费用大的现象。在数据集T10I4D100K、Mushroom 和Accidents上进行测试，测试结果表明，该MCFP－Tree算法频繁项集的挖掘效率明显优于Apriori算法和FP－Growth算法。

1 频繁项集的概念及相关理论

设I＝｛i1，i2，…，in｝是n个项目的全集，D 是事务数据库，事务T是I的子集，如：T＝｛i1，i2，…，im｝，此时T为m项集。每个事务T 都对应唯一的事务标识符TID。设有事务X，Y，有XI，YI，且X ∩Y ＝，则形如XY 的蕴含式就是一条关联规则，其中X，Y 分别为规则的前项集和后项集。如果D 中有a%的事务既包含X 又包含Y，那么则称规则的支持度为 a%， 对应的计算表达式为Support（XY）＝P（X ∪Y），即XY 同时出现的概率。

定义1 项集的支持度［10］为项集在数据库中出现概率，一般由人为设定，本文中支持度取值范围1%～90%。项集的支持数为项集在数据库中出现次数

定义2 给定最小支持数阈值MinSup，如果项集的支持数不小于该阈值，则该项集为频繁项集。如果频繁项集含有k个元素，则称为频繁k项集。

定理1 （频繁项集的反单调性［11］）如果一个项集的支持度小于最小支持度，则其是一个非频繁的项集，那么它的任何超集均为非频繁项集。反之，如果一个项集是频繁的，那么它的任意非空子集均为频繁项集。

Apriori算法核心：Apriori算法可分为两步：连接和剪枝。任取两个频繁k 项集，将其中各项按字典顺序排列，如p＝｛ti1，ti2，…，tik｝，q＝｛tj1，tj2，…，tjk｝，当满足ti1＝tj1，ti2＝tj2…，tik－1＝tjk－1，且tik≠tjk时，连接p，q产生的候选k＋1项候选项集为｛ti1，ti2，…，tik，tjk｝。剪枝则是利用了频繁项集的反单调性 （定理2），设有候选k＋1项集包含任意非频繁项或项集，则可直接判定其为非频繁项集，否则需要对数据库遍历进行支持数的统计，进一步验证其是否频繁。

CFP－Tree的构建：在CFP－Tree树中，每个节点由4部分组成：节点序号node－id、节点名字node－name、节点链node－sibling、计数数组［11］。其中计数数组中每个元素值均对应表示某一个项集的出现次数，例如C ＝｛c1，c2，…，ck｝是某个节点对应的计数数组，ci则表示全局频繁项目头表 （GlobalItemTable）中第i项到当前节点序号项的项集出现的次数。若当前节点序号为3，其计数数组C 为 ｛2，1，0｝，C 中第1项表示序号为1的节点到序号为3的节点的项集 ｛1，2，3｝在数据库中出现的次数为2次，C 中第2项表示项集 ｛2，3｝的出现次数为1次，C 中第3项表示项集｛3｝出现的次数为0次。

GlobalItemTable也由4部分组成：节点名字、节点序号、节点数目和节点指针。节点序号为从1 开始的整数，相当于GlobalItemTable中各节点名字的事务标志符；节点指针是从GlobalItemTable中每一项分别指向GlobalCFPTree中对应的同序号节点，该节点通过节点链指向下一个具有相同节点序号的节点。CFP－Tree 的构造算法ConstructCFP－Tree如下：

输入：数据库D，最小支持数MinSup

输出：GlobalCFP－Tree

（1）扫描数据库D，统计所有项出现的次数，将其与MinSup进行比较，将小于MinSup的项全部去除，剩余的频繁一次项按频次降序排列，依次对其添加序号，从1开始递增，形成GlobalItemTable。

（2）扫描数据库D，将D 中不属于GlobalItemTable的项去除，D 中保留下的均是频繁一次项，形成的新数据库叫D′。

（3）根据GlobalItemTable建立最左枝树。如从GlobalItemTable的第1项开始，该项指针指向一个新的节点，节点序号为该项在表中的序号1，节点名为该项在表中对应的名字，新节点链连接为空，计数数组长度为当前序号的大小，计数数组内元素全部置0。

（4）将D′中的数据按条读取，设第一条事务数据为｛a，b，c｝，首先将各数据项变换为GlobalItemTable中对应的序号，如 ｛1，3，2｝，再对其按大小进行升序排列，得到一条对应的数据项集 ｛1，2，3｝，叫mappedTrans，再调用第 （5）步中函数InsertToCFPTree，将mappedTrans插入CFP－Tree中。

（5）函数InsertToCFPTree。首先令FirstItem 为mappedTrans中第1 项，当前起始节点currNode 为GlobalItemTable中第FirstItem 个的项指针指向的节点。对于mappedTrans里每个元素i，如果currNode已经有序号为i的子节点，则将该节点计数数组的第FirstItem 项加1，否则创建一个序号为i的新节点，新节点的计数数组长度等于其父节点的计数数组长度，令该新节点计数数组的第FirstItem 项为1。

2 MCFP－Tree的提出

MCFP－Tree主要基于CFP－Tree紧凑的数据结构，改进了频繁项集的搜索方法，打破了候选项集生成－检验方法在含有较短频繁模式的大数据库下处理效率低下的劣势，使得算法具有更全面的适用性。

输入：数据库D 的CFP－Tree，CFPTreeD；全局频繁模式项目头表，GlobalItemTable；最小支持数阈值，Min－Sup；只包含频繁一项集的数据库，D’。

输出：D 中满足最小支持数的所有频繁模式FS。

中间变量：非频繁项集，NFS；候选频繁项集，CFS；局部频繁项目头表LocalItemTable中所有项对应的序号集合，LocalIdTable。

挖掘部分主程序：

（1）Procedure Mining

（2） Clear CFS

（3） For each frequent itemi∈ reversedGlobalItemTable

（4） Clear NFS

（5） ConstructLocalItemTable（i）

（6） If the size of LocalItemTable isnot 0

（7） Retraverse CFPTreeDto record the count of each item appeared with i

（8） Construct the LocalItemTable（i）

（9） Construct LeftMostBranch （i）

（10） Construct LocalCFP－Tree（i）

（11） MineFrequentItems（i）；

（12） Print all sets in FS

（13） End if

（14） End for

（15）End

算法从GlobalItemTable表中的最不频繁项集开始逆序遍历，在当前项基础上重新扫描数据库D’，统计当前项基础上各项的出现频次，寻找当前项基础上的频繁项，重新给他们赋予新的序号，从1开始，逐个递增，形成LocalItemTable，类比GlobalCFP－Tree的构造方法构造Local－CFP－Tree。在LocalCFP－Tree的基础上采用改进算法进行搜索频繁项集。

（1）Procedure MineFrequentItems（i）

（2） Clear CFS

（3） iterNum＝1； ／／the number of iteration

（4） For each node j∈LocalItemTable

（5） Attach the name of i and j into FS

（6） Attach the node－id j into LocalIdTable

（7） End for

（8） Sort the LocalIdTable in ascending order

（9） Scan the LocalIdTable to create all combination of two different node－id into CFS

（10） For each itemj∈CFS

（11） SearchforCount（j）；

（12） If the count＞＝MinSup

（13） Attach j into FS

（14） Else

（15） Attach j into NFS

（16） End if

（17） End for

（18） If the size of CFS isnot 0or 1

（19） Increment the count of iterNum

（20） Combination （CFS，i，iterNum）

（21） End if

（22）End

要搜索基于序号为i的频繁项的频繁项集，可以挖掘基于该项建立的LocalCFP－Tree，这棵子树中储存了所有满足MinSup的频繁项集。LocalItemTable中是基于该项的所有频繁1次项，若这些项的数目不大于1，则直接输出这些项与序号为i的项的组合，它们为输出频繁2次项；否则，采用Apriori算法候选项集的生成方法，按照候选项集的连接条件，调用Combination 函数，生成候选多项集，再调用SearchforCount函数计算候选项集的出现频数。

（1） Procedure SearchforCount（j）

（2） Count＝0；

（3） FirstItem＝the first of j

（4） LastItem＝the last of j

（5） Find the node k whose id is LastItem in LocalItemTable

（6） While the sibling of K is null

（7） K is the sibling of itself

（8） If the sum of countArray is not 0

（9） Attach all the parent of k to local root into parentList

（10） End if

（11） If parentList contains j

（12） If （the size of countArray of node K ＜FirstItem）

（13） Add up the values in the countArray of K

（14） Else

（15） Add up the value from countArray ［0］to countArray［FirstItem－1］

（16） End if

（17） End if

（18） End while

（19） End

（20） Procedure Combination（CFS，i，iterNum）

（21） Create new candidate frequent itemset newCFS from CFS according to Apriori’s candidate generation rule

（22） Clear CFS

（23） For each itemj∈newCFS

（24） If j not in the NFS

（25） If j＞＝MinSup

（26） Attach j into FS

（27） Attach j into CFS

（28） Else

（29） Attach j into NFS

（30） End if

（31） End if

（32） End for

（33） If the Size of CFS is not 0

（34） Increment the count of iterNum

（35） Combination （CFS，i，iterNum）

（36） End if

（37） End

SearchforCount函数的作用是计算候选项集j的支持数C。首先需要明确j的首元m 和尾元n，然后找到基于当前节点的LocalItemTable指向的最左枝，求得最左枝上序号为n的节点的计数数组中第m 项到n项的和c1。然后需要考虑节点n的节点链指向是否为空，如果为空则返回的C为c1；否则，该节点链指向的节点变为当前节点n，向上找到节点n的父节点链，并判断是否包含j，如果不包含则继续判断当前节点n的节点链指向是否为空，直到当前节点链指向的节点为空再跳出SearchforCount函数；否则c1要加上当前节点n父节点链中j出现次数c2。最后将所有的c1＋c2＋…的和返回给C，作为当前候选项集的出现次数。

为了方便理解，当搜索所有基于序号为i的频繁项的频繁项集结束后，输出的所有频繁项或项集均统一用节点名字或名字的组合表示。如要输出序号为5名字为x的频繁项的一个频繁项集 ｛1，2，3｝，项集支持数为 ｛10｝，该项集对应的节点名字为 ｛a，c，d｝，支持数也应为 ｛10｝，则输出结果应为 ｛a，c，d，x｝，支持数为 ｛10｝。下面我们给出一个事务数据库例子，用本文提出的改进算法MCFPTree进行挖掘。

例1：设事务数据库D 如果所示，最小支持度为40%（最小支持数为2），图1 为建立GlobalCFP－Tree之前的数据处理工作，数据库D 的GlobalCFP－Tree如图2所示。

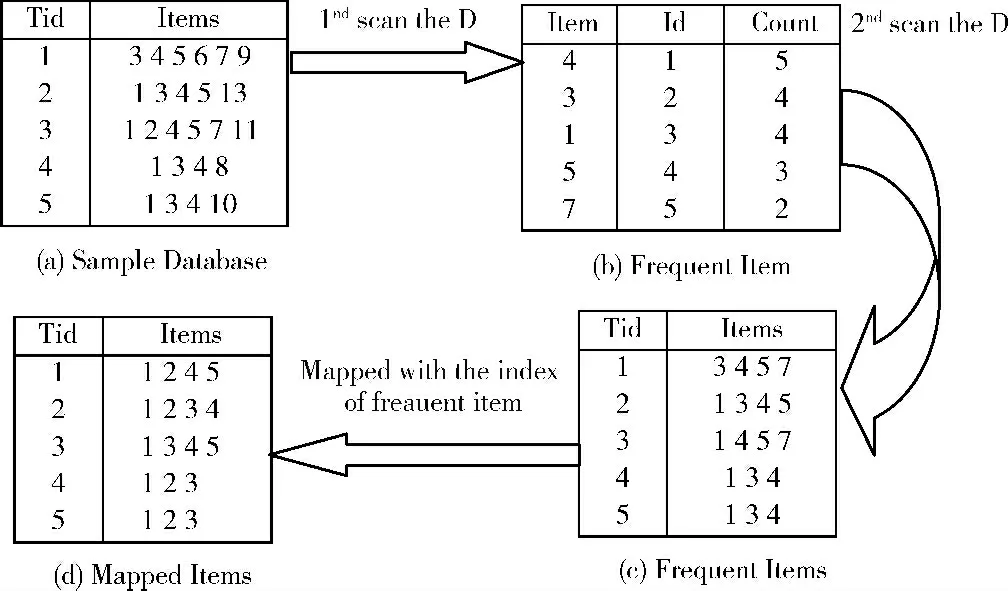
图1 事务数据库处理流程

图2 全局压缩频繁模式树GlobalCFP－Tree

样例数据库 （图1 （a）），首先遍历数据库，统计所有项出现的次数，找到频繁1 次项，将其按频次降序排列，每一个频繁项均对应一个Id号，从1开始，逐个加1，形成GlobalItemTable （图1 （b）），按照函数ConstructCFPTree建造最左枝树，根据该表重新扫描数据库，剔除非频繁项 （图1 （c）），并将所有频繁项一一对应到GlobalItemTable表中Id值，逐行升序排列 （图1 （d）），插入到GlobalCFP－Tree中。

从GlobalItemTable中最不频繁项 （序号为5的项）开始，该项由指针指向的节点计数数组为空，则继续沿节点链指向下一个同序号节点，找到第一条以序号为5节点为结尾的项集：｛1，2，4｝，沿节点链指向下一个节点，找到第二个项集： ｛1，3，4｝，此时该节点无下一个同序号节点，则以序号为5节点为结尾的项搜索结束。将找到的数据项集组合作为一个新的数据库newD，调用ConstructCFP－Tree方法建造基于序号为5 的节点的LocalItemTable和LocalCFP－Tree。遍历newD，得知项 ｛1 （4），2 （3），3 （1），4 （5）｝的支持数数分别为 ｛2，1，1，2｝，括号内为项的名字，和MinSup对比得知，只有名字为4，5的节点是基于序号为5节点的频繁项集，将其按支持数大小降序排列，并给每一项重新赋Id 值，形成新的LocalItemTable，根据该表重新调用函数ConstructCFP－Tree建立新的LocalCFP－Tree，如图3 （a）所示。

搜索以序号为5 的频繁项为基础建立的LocalCFPTree时，已知LocalItemTable中各项均为在其基础上的频繁1项集：｛｛1｝，｛2｝｝，支持数分别为 ｛2，2｝。则它们分别与该频繁项组合而成的输出频繁二项集名字为 ｛｛7，4｝，｛7，5｝｝，支持数为这两个节点在LocalItemTable里面的数量 ｛2，2｝。由于此时频繁1项集的个数大于1，可以调用Combination函数连接产生候选2项集 ｛｛1，2｝｝，调用搜索函数SearchforCount，我们可知其支持数为 ｛2｝，大于最小支持数阈值，所以这个候选项集是频繁2 项集，输出完整的频繁3项集的名字为 ｛｛7，4，5｝｝，支持数为 ｛2｝。

MCFP－Tree采用Apriori算法的候选项集产生机制，产生候选项集后直接搜索各个局部频繁模式树，比遍历数据库计数节省时间，效率得到显著提升。与FP－Growth相比，CFP－Tree数据结构更为紧凑，节点数目最多的时候可以减少为FP－Growth的一半，大大节约了系统内存的占用，此外搜索过程有效的减少对树的遍历，可以更高效的计算出候选项集的出现频次。

3 算法实现与比较

本文用java语言在内存2 G，CPU 为Intel（R）Core（TM）2Duo，32位的Windows7操作系统上实现了Apriori、FP－Growth、MCFP－Tree算法，使用了1组IBM 人工数据集T10I4D100K，2组经典测试数据集Mushroom、Accidents。

表1中，Mushroom 是从UCI机器学习数据库（http：／／archive.ics.uci.edu／ml／datasets.html）下载，Accidents、T10I4D100K数据集从频繁项集挖掘数据库（http：／／fimi.ua.ac.be／data／）下载。

图3 基于GlobalItemTable中频繁项建立的LocalCFP－Tree

表1 数据集

由于频繁项集数量在支持度范围30%～90%之间变化很大 （数量从几个至两千多个），为便于分析，我们统一对频繁项集的维数分布图在不同支持度时分别取以10为底的对数 （如图5、图8所示），缩小数量的变化范围。

Mushroom 最大事务长为23，所以很可能出现较多长频繁模式 （频繁模式的维数大于10）。由图4可知，MCFPTree网格区域所占面积远比同支持度时其它两种算法的面积小，结合图5，在支持度范围内，频繁模式的长度均较短（以长度不大于5的频繁模式为主），此时，改进算法效率远高于两种经典算法。在支持度为40%时，改进算法运行效率较Apriori算法提高了75.2%，较FP－Growth算法提高了76.1%。明显可以看出在处理含有较多短小频繁项集时，改进算法拥有显著的优越性。

图4 Mushroom 数据集的算法性能对比

图5 Mushroom 数据集频繁集的数量

下面两个数据集数据量分别为100000和340183，属于数据量很大的数据库，而且挖掘频繁项集的耗时在支持度范围内跨度较 Mushroom 更大，所以我们统一对T10I4D100K 和Accidents的性能对比图的纵坐标取log以10为底的对数，压缩时间的变化范围，如图6、图7所示。对Accidents的频繁项集维数分布图的纵坐标也取以10为底的log函数，如图8所示。

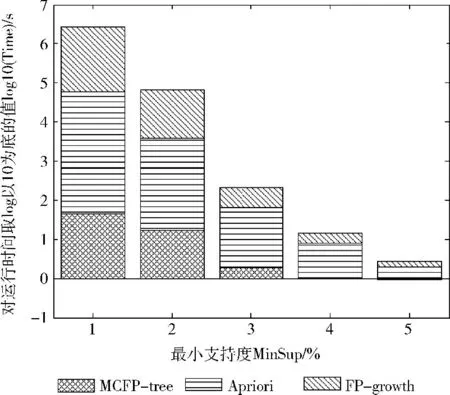
图6 T10I4D100K 数据集的算法性能对比

图8 Accidents数据集频繁项集的数量

T10I4D100K 是个数据量为100000的人工数据库，但在支持度大于5%时，它的频繁项集很少，所以我们取挖掘的范围为1%～5%。在支持度低于5%的时候，频繁项集的数目增加很快，还是以短小频繁模式为主，但是由于数据库变大，搜索时间相应就会变长，Apriori的运行效率显然明显低于其它两种算法。当最小支持度为3% 时，MCFP－Tree算法效率比Apriori算法提高了94%，比FPGrowth算法提高了40%，当支持度降为1%时，涌现较多长频繁模式，MCFP－Tree算法所占面积略小于FP－Growth算法，效率只比FP－Growth算法提高了3.6%。

结合表1和图8发现，Accidents的平均事务长度和频繁模式的长度都比Mushroom 更长，且此时数据库变得很大 （约为Mushroom 的66 倍），但是频繁模式还是以维度在10之内的频繁项集为主，证明Accidents数据库本身就是较为稀疏的数据库，此时改进算法所占面积比两种经典算法所占面积都小，运行效率也更高。在支持度范围内，改进算法比Apriori算法平均提高91%左右，比FP－Growth算法提高95%左右，由此可以看出MCFP－Tree更适合挖掘数据量大的稀疏数据库。

4 结束语

本文提出的MCFP－Tree算法融合了CFP－Tree的数据结构和Apriori算法的候选项集产生方法，可以显著提高频繁项集的挖掘效率，尤其是在含有较多较短的频繁模式的挖掘过程中 （大部分频繁模式的长度不超过10），可以取得更好的挖掘效率。但在有较多较长频繁模式时运行效率和FP－Growth接近，所以后续研究可以利用已经在Apriori类算法上发展起来的双向搜索策略分别对LocalCFP－Tree挖掘，提高算法的搜索效率，此外考虑到只挖掘GlobalCFPTree主树内存消耗会更少，后续可以针对主树来设计更加灵活的搜索算法，提高挖掘效率。

［1］YANG Zeming.Association rules incremental updating method based on cloud computing ［J］.Computer Engineering and Design，2014，35 （2）：504－508 （in Chinese）. ［杨泽明.云计算模型中关联规则增量更新方法 ［J］.计算机工程与设计，2014，35 （2）：504－508.］

［2］Wu H，Lu ZG，Pan L，et al.An improved apriori－based algorithm for association rules mining ［C］／／6th International Conference on Fuzzy Systems and Knowledge Discovery，2009：51－55.

［3］Yu WJ，Wang XC，Wang FY，et al.The research of improved apriori algorithm for mining association rules ［C］／／11th IEEE International Conference on Communication Technology Proceedings，2008：513－516.

［4］Li XC，Teng SH.The research on improvement of apriori algorithm based on mining frequent itemsets ［J］.Journal of Jiangxi Normal University （Natural Science Edition），2011，35 （5）：498－502.

［5］Gupta B，Garg D.FP－tree based algorithms analysis：FPGrowth，COFI－Tree and CT－PRO ［J］.International Journal on Computer Science and Engineering，2011，3 （7）：2691－2699.

［6］ZHOU Lijuan，WANG Xiang.Research on association rules algorithms based on cloud environment ［J］.Computer Engineering and Design，2014，35 （2）：499－503 （in Chinese）.［周丽娟，王翔.云环境下关联规则算法的研究 ［J］.计算机工程与设计，2014，35 （2）：499－503.］

［7］XIAO Jihai，CUI Xiaohong，CHEN Junjie.Mining N－most interesting itemsets algorithm based on COFI－Tree［J］.Computer Technology and Development，2012，22 （3）：99－102 （in Chinese）.［肖继海，崔晓红，陈俊杰.基于COFI－Tree的N－最有兴趣项目集挖掘算法 ［J］.计算机技术与发展，2012，35（2）：99－102.］

［8］Yudho GS，Raj PG.CT－PRO：A bottom－up non recursive frequent itemset mining algorithm using compressed FP－tree data structure［C］／／Proceedings of the IEEE ICDM Workshop on Frequent Itemset Mining Implementations，2004：212－223.

［9］Shen B.Research on the technology of association rules［M］.Hangzhou：Zhejiang University Press，2012：5－7.

［10］Liu B，Hsu W，Chen S，et al.Analyzing the subjective interestingness of association rules ［J］.IEEE Intelligent Systems and Their Applications，2000，15 （5）：47－55.

［11］Luo XW，Wang WQ.Improved algorithms research for association rule based on matrix ［C］／／International Conference on Intelligent Computing and Informatics，2010：415－429.