基于差分曲率的偏微分方程图像降噪算法

董婵婵，张 权，郝慧艳，张 芳，刘 祎，孙未雅，桂志国，2＋

（1.中北大学 电子测试技术国家重点实验室，山西 太原030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原030051）

0 引 言

目前图像降噪的方法众多，如基于偏微分方程 （partial differential equation，PDE）的图像滤波法［1，2］、小波滤波法［3，4］、非局部均值 （nonlocal means，NL－means）滤波法［5］等。其中，基于PDE的图像降噪算法能够较好缓解降噪和边缘保留之间的矛盾，逐渐成为图像降噪领域的研究热点。自从Perona－Malik提出各项异性扩散模型 （P－M 模型），基于PDE 的图像降噪算法引起了人们的广泛关注。P－M 模型利用梯度检测边缘，而噪声的梯度有时比边缘的梯度大，这使得处理后的图像仍含有噪声点。Chao等［6］在P－M 模型的基础上增加了图像灰度方差的信息，可以进一步去除图像中灰度方差较小的噪声；为了克服TV 模型的“阶梯”效应，Chen等提出了基于差分曲率的自适应全变分降噪算法［7］，算法提出新的边缘检测算子函数，有效避免了TV 模型的 “阶梯”效应；陈强等将片相似性思想引入到各向异性扩扩散降噪模型中［8］，使处理后的图像在去除噪声的同时，保留了更多的细节；Guo等提出了基于变指数的自适应P－M 图像降噪模型［9］，在图像的内部区域采用热传导方程，在图像的边缘处采用P－M 方程。为了避免二阶PDE产生的 “阶梯”效应，学者们利用高阶PDE对高频噪声平滑速度更快的特点，提出了四阶PDE 图像降噪算法［10－13］，本文将参考文献 ［10，13］中的四阶PDE 模型，分别记为Mahammad模型和Boli模型。受文献 ［6，7］的启发，本文提出了一种改进的各项异性扩散图像降噪算法，该算法可以使处理后的图像在去除噪声的同时保留更多的细节特征，提高图像降噪的性能。本文对该算法进行了分析与研究，并通过实验验证了其有效性和可行性。

1 Chao和Tsai算法及其不足

传统P－M 模型的表达式为

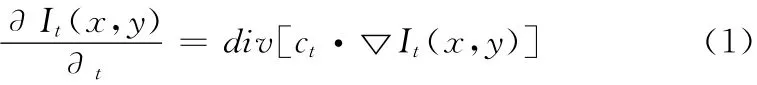
式中：ct——扩散系数函数，其表达式为

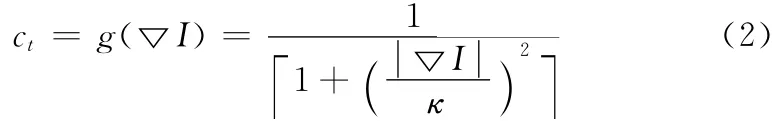
传统P－M 模型仅利用梯度来控制模型的扩散速度，而图像中有些平坦区域的梯度与细节处的梯度相差无几，因此只用梯度来检测边缘时不够的。Chao和Tsai指出，图像背景区域的方差远小于图像边缘，对传统的P－M 模型做出了改进，提出了新的扩散系数函数，如下所示

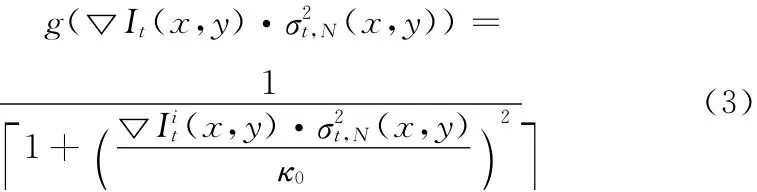
式中：σ2t，N（x，y）——归一化方差，其表达式为

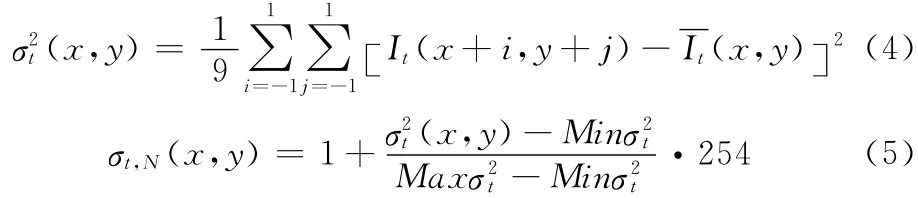
由于边缘处有较大的梯度值和方差，所以Chao和Tsai所提算法可以更好的区分边缘和背景，提高恢复图像的质量。

然而当图像含有噪声时，受噪声的影响，图像中有些背景区域的方差和弱边缘处的方差相差无几，甚至有些背景区域的方差比弱边缘处的方差稍大，如图1所示。

图1 含高斯噪声的lena图像

图1 （b）为中心坐标 （72，16），窗口大小 （3×3）的平坦区域的像素，图1 （c）为中心坐标 （143，56），窗口大小 （3×3）的细节区域的像素，其灰度值分别为

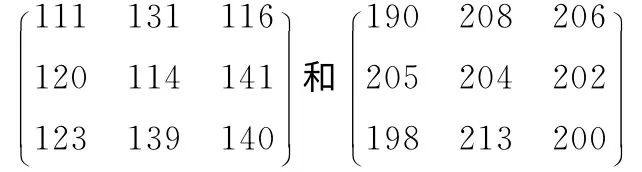
平坦区域的方差为：5.1966， 边缘处的方差为：2.2747。

对于上面的情况，若扩散强度不足，虽可以保留图像边缘，但方差大的背景区域的噪声去除不干净，会留有噪声点；若扩散程度过强，虽可以滤除背景区域的噪声，但同时会丢失图像的细节特征。因此，利用梯度和方差检测边缘的Chao和Tsai算法并不能很好的权衡噪声去除和细节保留之间的矛盾。

2 本文提出的算法

2.1 算法原理

文献 ［7］提出的差分曲率可以较好的区分细节和平坦区域、独立噪声，其表达式为

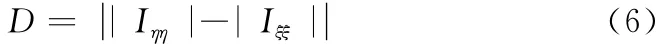
式中：Iηη和Iξξ——图像I在梯度方向和水平方向的二阶导数。梯度和切线方向的方向向量分别为

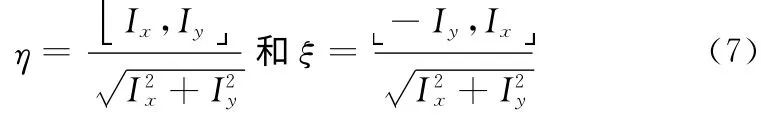
则

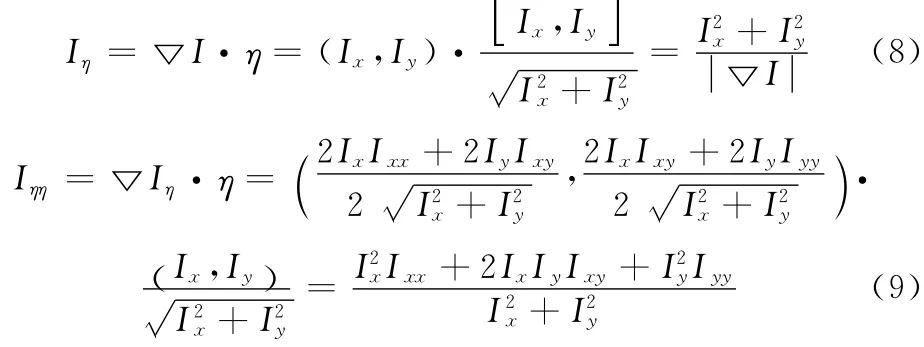
同理可得

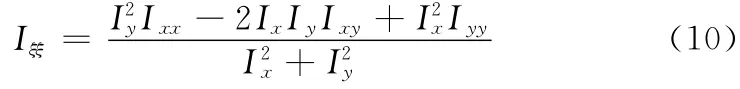
其中

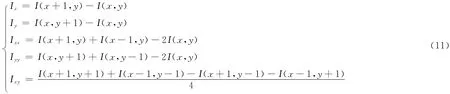
由式 （6）可知：在边缘处，｜Iηη｜较大，｜Iξξ｜较小，其差分曲率D 值较大；在平坦区域，｜Iηη｜和｜Iξξ｜都较小，所以D值较小；在独立噪声点处，｜Iηη｜和｜Iξξ｜都较大，且几乎相等，所以D 较小。因此根据差分曲率D值大小，可以很好的区分边缘和平坦区域、独立噪声点。

根据图1 （b）平坦区域和图1 （c）弱边缘的灰度值，由式 （7）～式 （11）计算其差分曲率：

平坦区域

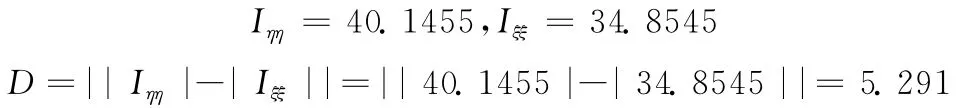
弱边缘处

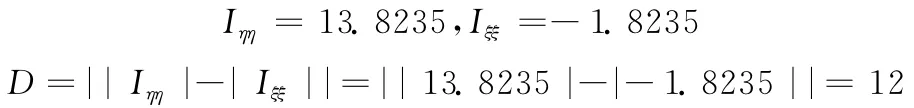
由上面的计算可知，即使在弱边缘处差分曲率的值也比平坦区域的值大，而由上节图1灰度方差的计算结果可知，灰度方差无法很好的区分弱边缘和噪声，即差分曲率区分弱边缘和平坦区域的能力优于灰度方差。因此，本文提出新的扩散系数函数如下

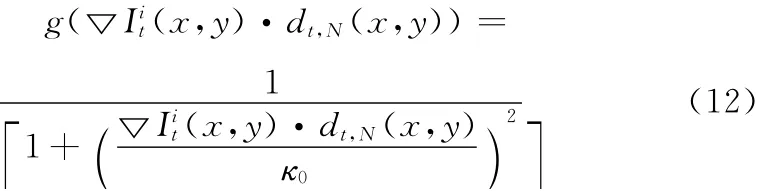
式中：dt，N——归一化差分曲率

此时，各项异性扩散方程为

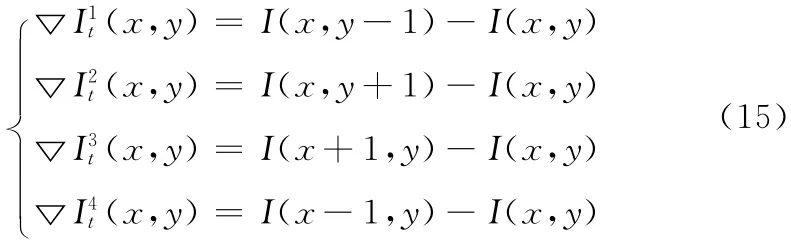
2.2 算法步骤

（1）首先由式 （7）～式 （11）计算梯度方向和切线方向的二阶导数Iηη和Iξξ。

（2）将第一步计算的值带入式 （6），可计算出差分曲率D，并可由式 （13）得出归一化差分曲率。

（3）由表达式 （15）得到4个方向的梯度值。

（4）把第二步和第三步计算的值带入式 （12），得到扩散系数函数的值。

（5）最后依据表达式 （14）对图像进行处理。

（6）重复上述步骤 （1）～步骤 （5），直至得到较好的恢复图像I。

3 实验结果与分析

本文采用256×256的lena标准图像作为测试图像，图2为本算法与P－M 模型、TV 模型、Chao和Tsai模型的比较分析；为了更清晰的展示各模型降噪效果，图3给出了图2对应模型处理结果的局部放大图像；图3为本算法与LLT 模型、模型、模型的比较分析。

图2 （a）为lena原始图像，图2 （b）为加入方差为0.002的高斯噪声图像，图2 （c）～ （f）分别为经过P－M模型、TV 模型、Chao和Tsai模型以及本文提出模型的处理结果图像。图3为图2中各模型处理结果的局部放大图。与P－M 模型处理结果相比，Chao和Tsai所提模型处理图像的毛发的细节保留的更多，如图2 （c）和 （e）所示。由图2和图3中的图 （c）、（e）和 （f）可以看出，P－M 模型和Chao和Tsai模型处理后的图像均含有斑点噪声，且帽子上的细节纹理丢失较多，而本文算法处理后的图像帽子上的细节纹理很清晰，且不存在噪声点。由图3中各模型处理结果的局部放大图可以清晰的看出，图3 （f）与图3（c）、（d）和 （e）相比，本文算法处理后的lena图像帽檐上保留的细节纹理较多且清晰，从而提高了图像质量。

从图4可知，LLT 模型丢失了很多细节，图像较模糊；如图4 （d）所示，Bibo模型处理后的lena图像帽子上的纹理被平滑，也丢失了重要的细节信息，但与图4 （c）LLT模型相比，Bibo模型比传统的LLT 模型保留了更多边缘；将图4中的LLT 模型和Bibo模型与图4 （f）本文算法相比可以清晰的看出，本文算法处理后的图像保留了更多弱边缘和纹理等细节特征，如lena图像的头发和帽子上的褶皱纹理都比较清晰；图4 （f）与图4 （e）相比，虽然处理后的图像都保留了较多的边缘和细节，但Mohammad模型的计算较复杂，运算量较大。

为了对算法进行客观、定量的评价，本文采用较常用的

图2 本文算法与二阶PDE模型的处理结果

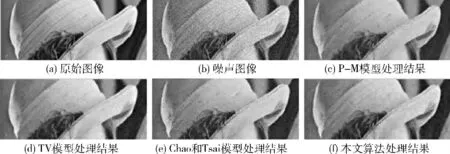
图3 本文算法与二阶PDE模型处理结果的局部放大图

图4 本文算法与四阶PDE模型的处理结果

信噪比、平均绝对误差、峰值信噪比来评价处理后图像的质量。这些参数的定义如下：

（1）信噪比 （signal to noise ratio，SNR）

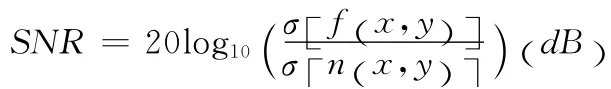
式中：σ［f（x，y）］和σ［n（x，y）］——图像和噪声的标准方差。信噪比越高，图像的质量越好，噪声越少。

（2）峰值信噪比 （peak signal to noise ratio，PSNR）

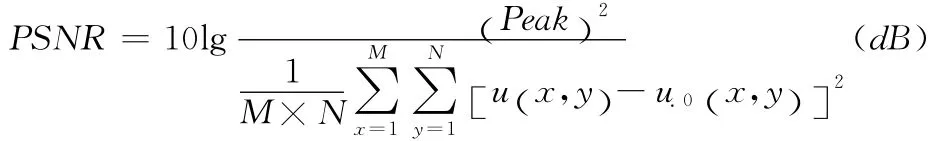
PSNR是图像信噪比变化情况的统计平均，PSNR 值越大，图像失真越少。在8 位量化的灰度图像中，通常取Peak ＝255。

（3）平均绝对误差 （mean absolute error，MAE）

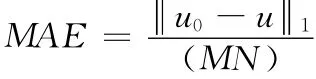
式中：M，N——图像大小，u0——原始图像，u——恢复图像。MAE——去噪后图像与原始图像之间的差异，MAE越小，去噪效果越好。

表1列出了本算法与其它算法的图像质量评估参数，由表1可以看出：本文提出算法与其它算法相比，信噪比SNR 和峰值信噪比PSNR 都较大，平均绝对误差MAE 较小。说明本算法处理后的图像质量较好，能够有效地去除噪声，并保留图像的边缘等重要细节特征。

表1 不同降噪算法处理后的质量评估参数

4 结束语

本文针对Chao和Tsai提出降噪模型的不足，构造出新的扩散系数函数，提出了改进的各项异性扩散模型。新的扩散系数函数可以更好的区分弱边缘、噪声点和平坦区域，进而算法可以在弱边缘、纹理等细节处减小平滑，在噪声点和平坦区域增强平滑。实验结果表明，本算法可以较好的权衡噪声去除和细节保留之间的矛盾，即可以在滤除噪声的同时，保留较多的弱边缘信息。从主观的视觉效果和客观的质量评价可以看出，算法的降噪效果优于Chao和Tsai提出模型、P－M 模型和TV模型、LLT模型、Bibo模型、Mohammad模型。因此，本文提出的算法对图像降噪有较好的效果，对图像进一步的处理与研究有一定的意义。

［1］WANG Yan，GUI Zhiguo，ZHANG Quan，et al.Image denoising of PDE based on local intuitionistic fuzzy entropy ［J］.Computer Engineering and Design，2013，34 （12）：4256－4260（in Chinese）.［王艳，桂志国，张权，等.基于局部直觉模糊熵的偏微分图像降噪算法 ［J］.计算机工程与设计，2013，34（12）：4256－4260.］

［2］DAI F，ZHENG N，XUE J.Image smoothing and sharpening based on nonlinear diffusion equation ［J］.Signal Processing， 2008，88 （11）：2850－2855.

［3］ZHONG J，SUN H.Wavelet－based multi－scale anisotropic diffusion with adaptive statistical analysis for image restoration［J］.IEEE Transactions on Circuits and Systems，2008，55（9）：2716－2725.

［4］WANG Kai，LIU Jiajia，YUAN Jianying，et al.Noise reduction of optimization weight based on energy of wavelet sub－band coefficients［J］.Journal of Computer Applications，2013，33（8）：2341－2345 （in Chinese）.［王凯，刘甲甲，袁建英，等.基于小波子带系数能量的优化权值降噪 ［J］.计算机应用，2013，33 （8）：2341－2345.］

［5］ZHONG Ying，YANG Xuezhi，TANG Yiming，et al.Nonlocal means denoising derived from structure－adapted block matching ［J］.Journal of Electronics ＆Information Technology，2013，35 （12）：2908－2915 （in Chinese）. ［钟莹，杨学志，唐益明，等.采用结构自适应块匹配的非局部均值去噪算法 ［J］.电子与信息学报，2013，35 （12）：2908－2915.］

［6］Shin－Min Chao，Du－Ming Tsai.An improved anisotropic diffusion model for detail－and edge－preserving smoothing ［J］.Pattern Recognition Letters，2010，31 （13）：2012－2023.

［7］CHEN Q，Montesinos P，SUN Q，et al.Adaptive total variation denoising based on difference curvature［J］.Image and Vision Computing，2010，28 （3）：298－306.

［8］CHEN Qiang，ZHENG Yuhui，SUN Quansen，et al.Patch similarity based anistropic diffusion for image denoising ［J］.Journal of Computer Research and Development，2010，47（1）：33－42 （in Chinese）.［陈强，郑钰辉，孙权森，等.片相似性各项异性扩散图像去噪 ［J］.计算机研究与发展，2010，47 （1）：33－42.］

［9］GUO Z，SUN J，ZHANG D，et al.Adaptive Perona－Malik model based on the variable exponent for image denoising ［J］.IEEE Transactions on Image Processing，2012，21 （3）：958－967.

［10］Mohammad RH.An anisotropic fourth－order diffusion filter for image noise removal ［J］.Springer Science＋Business Media，2011，92 （2）：177－191.

［11］ZHANG J，LI L，YANG J.An enhanced fourth－order PDE model based on Laplacian and gradient operator［C］／／IEEE 12th International Congerence on Computer and Information Technology，2012：144－146.

［12］LIU X，HUANG L，GUO Z.Adaptive fourth－order partial differential equation filter for image denoising ［J］.Applied Mathematics Letters，2011，24 （8）：1282－1288.

［13］LU B，LIU Q.An edge－preserving fourth order PDE method for image denoising ［C］／／2nd International Conference on Advanced Computer Control. Shenyang：IEEE，2010：153－157.