高效动态存储再分配方案与实现

胡平平，王晶杰

（北京信息科技大学 自动化学院，北京100192）

0 引 言

传统的动态存储管理 （DMM）有首先适配法、再次适配法、最佳适配法和最坏适配法4种方法［1］，许多文献也提出了各种改进算法以提高DMM 的性能，如利用二叉树来管理内存分区以提高DMM 的效率［2］；利用虚拟内存管理实现DMM，以便有效降低时间耗费［3］；改进DMM 算法降低分配失败率［4］、或改善内存泄漏［5］、或改进动态内存分配的脆弱性并提高内存分配安全性［6］等。有些研究者则注重不同应用对DMM 需求的差异，希望找到其需求特性以提供最佳策略［7－9］。文献 ［10］通过模拟应用的内存分配需求，从所提供的多种分配方法中选择最适合的，以便在存储区使用量和处理功耗方面取得好的效果。这些改进措施可分为两类：一类是在系统级对DMM 进行改进，使其对各种动态存储的需求都具有较优的性能；另一类则针对具体应用的特性，分别提供不同的最佳方法。

笔者发现，在需要连续存储大量大小和数量均不确定的数据时，若直接使用系统的DMM 实现，其空间利用率和执行效率都比较差。为此，本文提出了动态存储再分配（DMRA）方案，该方案有效地减少了对系统DMM 的执行次数，不仅明显提高了存储空间的利用率，还极大地提高了存储空间的分配速度。

本文以VC＋＋6.0控制台应用程序为例，先分析指出了常规动态存储分配存在的问题，然后介绍了DMRA 方案和实现算法，在对其性能进行了简单的理论分析之后，用多个实例数据进行了测试，最后给出了改进方案和注意事项。实例数据的测试结果表明该方案能节省36%至75%的存储空间，而分配速度则提高了20～50倍。

1 常规动态存储分配存在的问题

C语言实现DMM 的基本函数是malloc（），VC＋＋系统又为其提供了DEBUG （以下简称D 版）和RELEASE（以下简称R 版）两种不同版本的代码。malloc（）每分配一块存储空间，都要使用一些额外的空间以实现DMM，两种版本代码所使用的额外空间和执行时间不同，因此其效率也不相同。如要分配长度是L 字节的空间，实际使用的存储空间长度AL 为

两种版本的BaseL 都是8 （实际上是链表两个指针占用的空间），R 版的ExtraL 为0，D 版的ExtraL 是36 （实际上是一个32字节的信息头和4字节的安全预留），即：

D 版

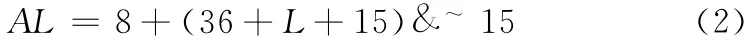
R 版

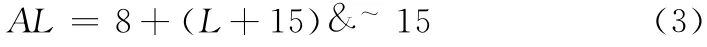
令WL＝AL－L，这就是每次内存分配的浪费空间，D版的WL 在44 （L%16＝12时）至59 （L%16＝13时）之间；而R 版的WL 在8 （L%16＝0 时）至23 （L%16＝1时）之间。显然，在L 较小时WL 与L 相比还是很可观的，若用malloc（）为大量小长度数据申请动态存储空间，则会导致系统存储空间的巨大浪费。

在比较不同处理方法的执行时间时，处理所执行的CPU 指令数量是较可靠的依据。由于本文仅涉及动态储存连续分配的情况 （即分配结束前不释放任何所分配的空间），因此下面仅对malloc（）函数被连续调用的情况进行分析。跟踪分析发现，malloc（）代码的执行由下面3部分构成

其中，BaseI是固定执行的指令数量，ScanI 是执行串扫描指令的重复次数，StosI 是执行串存储指令的重复次数。malloc（）对存储区的处理是以4KB 为单位进行的，其过程按当前要分配存储区长度的不同可分两种情况 （用图1来说明）。图中每个粗矩形框表示一个4KB 存储区域，左边为低地址，阴影部分为已分配的空间，P0为当前可分配空间的起始位置，B1和B2分别为P0后面两个4KB 存储区的边界位置。

图1 malloc（）对存储空间的处理方法

情况1：分配空间的结束位置为P1，也即可与P0在同一个4KB内完成分配。ScanI的处理是扫描P0至B1之间是否为0xFEEEFEEE （以下简称DD1），StosI 的处理分3部分：第一部分是将P1至B1之间填充为DD1，第二部分是将P0至P1之间填充为0xBAADF00D，第三部分 （仅D版）是将P0至P1之间实际申请长度的空间填充为0xCDCDCDCD。

情况2：分配空间的结束位置为B1之后的P2，即不能与P0在同一个4KB内完成分配。ScanI的处理有两部分，StosI的处理则有4部分，依次是：扫描P0至B1之间是否为DD1，将P0至B2之间填充为DD1，扫描P0至B2之间是否为DD1，将P2至B2之间填充为DD1，将P0至P2之间填充为0xBAADF00D，（仅D 版）将P0至P2之间实际申请长度的空间填充为0xCDCDCDCD。

上述串指令的重复次数不仅和P1的位置有关，还和申请长度有关，本文涉及的分配长度有两类，分别为1至255（平均长15至25）和固定长度2048，因此B1和B2一定是相邻的两个4KB区域。下面以第一类情况1的D 版为例，说明其平均指令数量的求解方法。

首先固定执行的指令数量BaseI＝716；扫描区域最短8，最长4KB－8，平均长2KB，按双字为单位扫描，扫描指令平均重复次数为512；同理，第一次填充指令的平均重复次数也为512；第二次填充区域长度为申请长度与16B对齐后加0x30，最短64，最长304，平均184，平均重复次数为46；第三次填充区域最短4，最长256，平均长130，平均重复次数为32。因此，申请长度为1至255情况1的D版malloc（）所执行指令的平均总数量为2076。同理可以计算出情况2的D 版执行指令的平均总数量为3560。至于情况1和情况2出现的概率应该按平均申请长度15至25来计算，其实际使用空间的长度是72。因为储存分配的间隔是8的倍数，按均匀分布在4 KB 范围内计算，则共有1024种情况，其中只有72／8＝9 种会导致情况2。因此，申请长度为1至255的D 版malloc（）执行指令总数量的平均为：2076· （1024－9）／1024＋3560·9／1024＝2089。同样方法可以计算出其它情况下malloc（）函数执行的指令数量，见表1。

表1 各种情况下malloc（）函数执行指令的数量

DMM 之所以需要额外的存储空间并执行相对复杂的操作，是为了较好地满足复杂的储存申请和释放需求。但在实际应用程序中，经常需要连续动态存储大量的短长度数据，且在完成所有数据的储存之前，不需要释放任何空间。在这种情况下，若用malloc （）为每一个数据申请空间，不仅会导致系统存储空间的巨大浪费，而且还执行了大量没必要的操作。为解决这个问题，本文提出了一种动态储存再分配方案，可以有效改善该情况下动态储存的空间利用率和执行效率。

2 DMRA 方案

所谓动态储存再分配方案是将零散的动态储存申请转换为集中申请，并利用简单的本地分配策略对已申请的存储空间进行有效的再分配。现以短数据连续动态储存为例加以说明。

图2是用malloc（）连续为N 个短数据单独申请存储空间的分布情况。其中P1至PN为申请到的N 个数据储存区域的指针，每个实箭头线表示一次对malloc （）函数的调用，得到的存储区域用粗线矩形表示，其阴影部分为DMM 占用的额外空间。

图2 为N 个短数据单独申请存储空间的分布

图3 DMRA 方法为N 个短数据申请存储空间的分布

从上图可以看出，DMRA 方案具有更高的存储空间利用率和较少的malloc（）调用次数，而本地分配处理非常简单，因此DMRA 将具有更快的速度。

3 DMRA 的实现

DMRA 的实现要在满足应用需求的前提下保证其执行速度。由于数据的数量N 不确定，因此存储块的数量M 也不确定，指针BPi必须用动态数组储存。虽然C＋＋提供了vector模板类可以方便地实现动态数组，但其效率非常低，因此本文直接利用realloc （）实现BPi的动态储存。为了使用方便，DMRA 仅需实现一个和malloc（）完全相同函数，其原型为：

void＊DMRAalloc（size＿t size）；

实现DMRA 算法需要设置的常量和变量以及各变量的初始值如下所示：

＃define INC＿BLK＿NUM 128 ／／Bpi动态数组递增长度

＃define BLK＿LEN 2048 ／／每个存储块的长度

char＊＊pBP＝NULL； ／／Bpi动态数组指针

int BPLen＝0； ／／Bpi动态数组长度

调查显示，创业的动机包括获得财富、自我实现、亲友支持、社会支持，创业动机与少数民族大学生创业能力正相关，相关系数为0.72，其中，自我价值实现与创业力相关性最显著。

char＊CntMemBuf； ／／当前存储块首地址

int BlkIdx＝－1； ／／当前使用的存储块下标

int NextPos＝BLK ＿LEN； ／／当前存储块下一个地址

基本DMRAalloc（）函数的实现流程如图4所示，pBf是该函数仅有的一个局部指针变量。从各变量的初始值可以看出，第一次调用该函数将自动调用malloc （）申请第一个存储块，同时也将第一次调用realloc（）为存储块指针分配空间。而本地分配处理则简单到仅有两次加法赋值和一次判断。

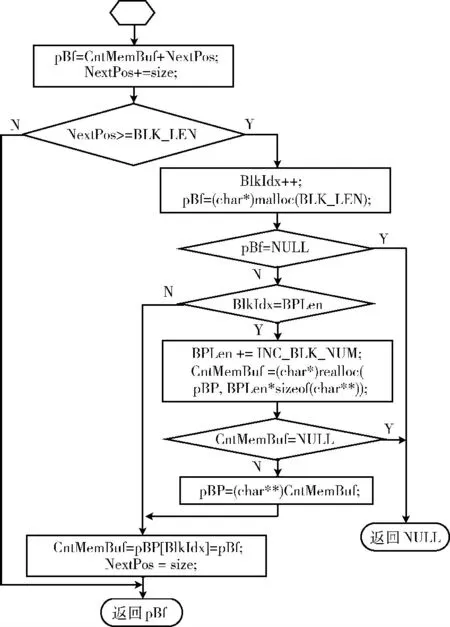
图4 基本DMRA 算法的流程

4 DMRA的设计要点

为了保证DMRA 算法的正确性及较高的空间利用率，必须注意下述设计要点：

（1）BLK＿LEN 必须大于等于所申请存储空间的最大长度。

（2）DMRA 算法的空间利用率和BLK＿LEN 与平均申请长度的比成正比。

（3）每个存储块后部的剩余空间没有使用，最坏情况下，该剩余空间是最大申请长度减一。

（4）在总申请空间小于存储块长度情况下，DMRA 的空间利用率反而会比直接用DMM 低。

（5）DMRA 算法没有考虑存储空间起始地址的对齐问题。实际上，若要与A＝2k对齐，只需将NextPos＋＝size改为NextPos＝ （NextPos＋size＋A－1）＆～（A－1），将NextPos＝size改为NextPos＝ （size＋A－1）＆～（A－1）即可。

（6）当不再使用由DMRA 申请的存储空间时，必须将动态数组pBP中的BlkIdx＋1个指针都释放掉。为了尽量保证系统存储空间的连续性，建议按倒序的顺序释放，最后还要释放指针pBP。

5 DMRA 的改进

基本DMRA 算法只能完成一次多存储区的连续分配，在实际应用中，当处理完这些数据后，常需对同类型的其它数据进行相同的处理。虽然可以将DMRA 所申请的存储块释放后重新初始化变量再次使用，但这样没有充分利用DMRA 执行效率的优势。改进的DMRA 算法不仅能实现多次连续分配，而且使后续分配具有更高的执行效率。其原理是：不释放DMRA 已申请的存储区，仅通过变量的重新设置，实现多次连续存储DMRA 已申请空间的再使用。为此，仅需再设置一个表示Bpi动态数组中已申请存储块的数量BlkNum，其初始值为0，并对基本DMRA 算法进行改进，如图5所示。

再次使用DMRA 算法连续为其它数据分配空间前需要进行下述设置：

如果BlkNum 非零 （表示上一次DMRA 至少为一个数据分配了空间），则将BlkIdx和NextPos 清零，并将Cnt－MemBuf设置为pBP ［0］；如果BlkNum 为零，则不用改变任何变量的值。这样，新数据的空间将从上次第一个存储块开始分配。若新数据使用的空间没有上次大，则不需要申请任何新的存储块；当新数据空间比上次大时，DMRA会继续申请新的存储块，直到满足需求为止。

跟踪测试得出改进的DMRA 算法函数在各种情况下执行指令的数量如表2所示，其中的3473和2679使用了表1的最后一列数据，且假设realloc（）和malloc（）函数的数据一样。

将表2第二列数据与表1第四列数据对比，对于为长度在1至255的数据分配存储空间时，DMRA 本地分配的执行速度分别是直接调用malloc（）的近44 （2089／47）和127 （1781／14）倍，可见DMRA 有非常快的执行速度。

6 DMRA 性能的实际测试

与常规DMM 性能相比，DMRA 的改进程度与许多因素有关，下面以实际测试的数据为例加以说明。本实例用DMRA 方法为储存大量随机长度的文件名称字符串分配空间，这些文件可能是一个磁盘或一个文件夹中的所有文件。

图5 DMRA 改进算法的流程

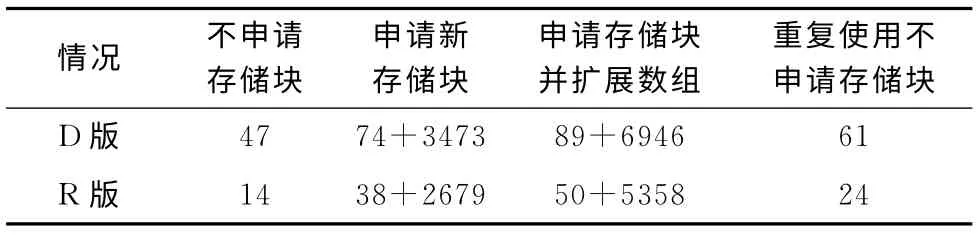
表2 改进的DMRA 算法函数各种情况执行指令的数量

WindowsXP系统下文件名称的长度从1至255不等，数量从几百至几万不等，非常适合于用本文介绍的DMRA 方法为之分配存储空间。

测试程序对所处理的文件数量和文件名长度进行了统计，按式 （2）和式 （3）计算出每一个文件名实际使用的空间，求和则是直接用malloc （）分配所用的空间。根据DMRA 处理所使用的存储块数量则可直接算出使用DMRA分配所用的空间。

在执行时间方面，直接分配的时间是文件数量乘以单个malloc（）的平均执行指令数量，而DMRA 的时间则分别是：

D 版

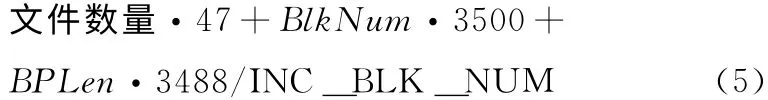
R 版

其中，3500和2703是表2第三列与第二列的差，3488 和2691则是第四列与第三列的差，分别表示为申请存储块和动态数组而额外执行的指令数量。

表3是对5个不同对象的实际测试数据，表4则是他们的对比结果。图6和图7分别是第二和第三个对象文件名长度的分布图 （由测试程序自动生成）。

表3 5个不同对象的实际测试数据

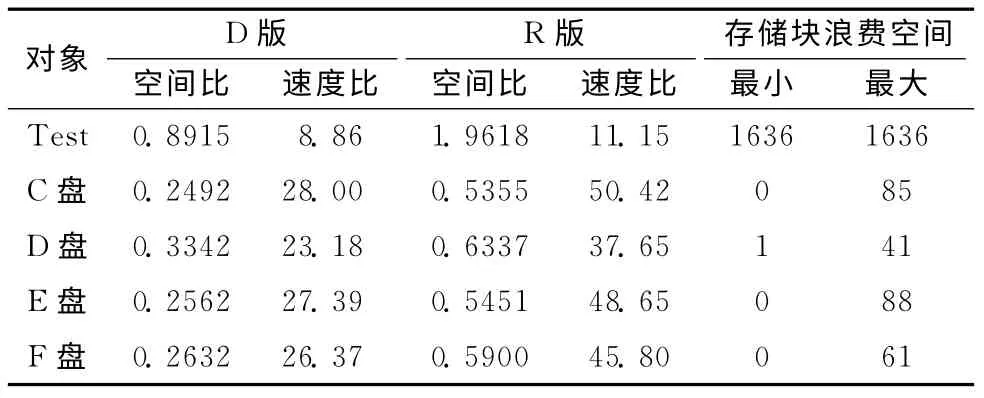
表4 5个不同对象DMRA与直接分配方法的空间和速度比

图6 C盘文件名长度的分布图和基本数据

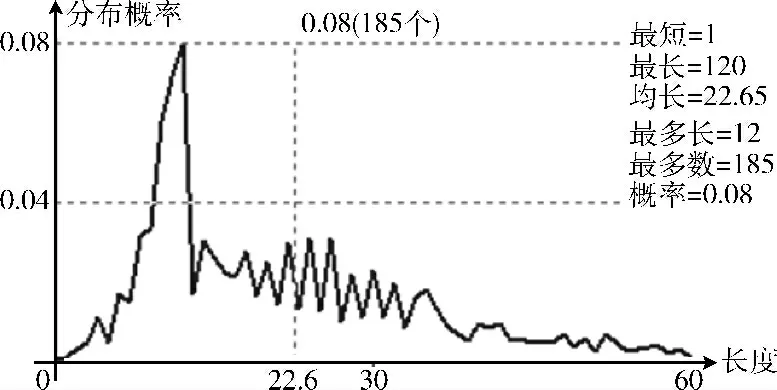
图7 D 盘文件名长度的分布图和基本数据

当DMRA 用于多次连续存储区分配时，在无需申请新存储块的情况下，与直接分配的速度比是常数，D 版为2089／61＝34.25，而R 版则为1781／24＝74.21。

表4和表5中第一个对象是个用于测试的数据，其中仅含不同长度的文件37个，由于仅需一个存储块，且该存储块尚有1636个空间没有使用，因此其空间利用率最小，R 版下甚至还不如直接分配 （几乎比直接分配还多用一倍的空间），可见，DMRA 在数据量少的情况下，并无优势。后4个对象的数据量很大，实际数据表明，D 版DMRA 使用的空间才几乎是直接分配方法的1／4 （24.9% 至33.4%），R 版则是直接分配方法的一半多一些 （53.5%至63.3%）。速度方面，DMRA 在各种情况下都有较大的优势，D 版DMRA 的速度是直接分配方法的23至28倍，R版则是更高的37至50倍。

7 结束语

本文对需要连续为大小和数量均不确定的海量数据动态分配存储空间的问题进行了研究，在细致分析了直接利用malloc（）存在的问题后，提出了一种高效的动态存储再分配方案，并给出了实现该方案的高效算法。实际测试结果表明，该方案有效地减少了系统动态存储管理的执行次数，在明显节省系统存储空间36%至75%的同时，分配速度提高了20～50倍，在重复多次使用的情况下速度提高最多达70倍，该方法在作者开发的多个以磁盘文件为处理对象的软件中得到应用，效果明显。

［1］LI Jun.A brief analysis on dynamic memory management in C／C＋＋program ［J］.Xinjiang Radio and TV University Journal，2009，13 （2）：53－54 （in Chinese）.［李军.浅析C／C＋＋程序运行过程中的动态存储管理 ［J］.新疆广播电视大学学报，2009，13 （2）：53－54.］

［2］HU Bin，SUN Jianli，ZHANG Yongping，et al.Research and implementation of technique for memory management ［J］.Computer Engineering and Design，2007，28 （5）：1226－1228（in Chinese）.［胡滨，孙健力，张永平，等.一种内存管理技术的研究与实现 ［J］.计算机工程与设计，2007，28 （5）：1226－1228.］

［3］WEI Haitao，JIANG Yuming，LI Jianwu，et al.Research of high efficient implementation of memory management mechanism ［J］.Computer Engineering and Design，2009，30 （16）：3798－3712 （in Chinese）.［魏海涛，姜昱明，李建武，等.内存管理机制的高效实现研究 ［J］.计算机工程与设计，2009，30 （16）：3798－3712］.

［4］Zhao Feimeng，Shu Dong Zhang.Buddy algorithm optimization in linux memory management［J］.Applied Mechanics and Materials，2013，2746 （423）：746－2750.

［5］Varlese，Marco.Improving performance for dynamic memory allocation［J］.Embedded Systems Design，2009，22 （5）：21－29.

［6］Yves Younan，Wouter Joosen，Frank Piessens.Improving memory management security for C and C＋＋ ［J］.International Journal of Secure Software Engineering，2010，1 （2）：57－82.

［7］Florence Charreteur， Bernard Botella， Arnaud Gotlieb.Modelling dynamic memory management in constraint－based testing ［J］.Journal of Systems and Software，2009，82 （11）：1755－1766.

［8］Marja del Mar Gallardo，Pedro Merino，David Sanon.Model checking dynamic memory allocation in operating systems［J］.Journal of Automated Reasoning，2009，42 （2）：229－264.

［9］Jose L Risco－Martin，Manuel Colmenar J，Ignacio Hidalgo J.A methodology to automatically optimize dynamic memory managers applying grammatical evolution ［J］.The Journal of Systems ＆Software，2014，91 （1）：109－123.

［10］Jose L Risco－Martin，Manuel Colmenar J，David Atienza.Simulation of high－performance memory allocators ［J］.Microprocessors and Microsystems，2011，35 （8）：755－765.