不确定性数据的超球支持向量机分类方法

李文进，熊小峰，毛伊敏

（1.江西理工大学 理学院，江西 赣州341000；2.江西理工大学 应用科学学院，江西 赣州341000）

0 引 言

在数据分类领域，现有方法的研究往往是针对确定性数据提出，不能直接用于处理不确定性数据，且数据的不确定性对分类结果的可靠性具有不可忽视的影响，因此面向不确定性数据分类方法的研究具有重要的意义［1－3］。

针对属性级不确定性数据［2，3］的分类问题，国内外的研究方兴未艾，并取得一定具有代表性的研究成果，主要有基于决策树的不确定性数据分类方法［4］、基于朴素贝叶斯的不确定性数据的分类方法［5，6］、基于规则的不确定性数据分类方法［7］等。现有基于支持向量机 （SVM）分类方法的研究主要基于随机理论，视样本为满足某种已知分布的随机变量［8，9］。文献 ［10］提出USVC、AUSVC 及MPSVC3种方法，这3种方法均采用多维高斯分布描述数据的不确定性。其中，USVC算法建立了SVC分类器的不确定性机会约束规划问题，并将问题转化为二阶锥规划求解问题。AUSVC 方法和MPSVC 方法均基于USVC 方法求解基本解，并通过特定手段迭代调整各训练样本对应的机会约束的置信参数，从而减小噪声样本对分类器的影响。

基于随机理论的方法需要大量的样本信息来构建概率分布函数。然而，实际工程应用中满足随机性假设要求的样本数据通常是缺乏的，但不确定性信息的界限却容易获得［8］，这类不确定性被称为非概率有界不确定性［3，8，9］，所对应的数据称为区间不确定性数据。标准结构支持向量机是针对二分类提出的，在处理多分类时具有计算复杂度较高的局限［11］。超球支持向量机是一种具有较低计算复杂度的球结构支持向量机分类方法［12－14］。

因此，针对区间不确定性数据分类问题，本文基于球结构支持向量机，提出了区间不确定性超球支持向量机（interval uncertainty hyper－sphere support vector machine，IUHSVM）。仿真结果表明，该算法具有一定的抗不确定性噪声干扰的能力，且具有较优的分类精度和鲁棒性。

1 不确定数据模型

1.1 区间数的基本概念

非概率有界不确定性在科学研究和工程实际中有广泛的应用背景，往往采用区间数描述。区间数通常定义为一对有序的实数［3，8，9］

式 （1）中UR表示区间上界，UL表示区间下界，若有UR＝UL，则该区间退化为实数。记I（R）一维区间数集合，UI也可以定义为如下形式

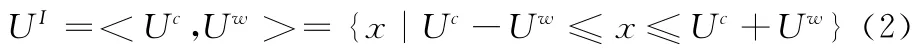
式 （2）中Uc和Uw分别表示区间UI的中点和半径

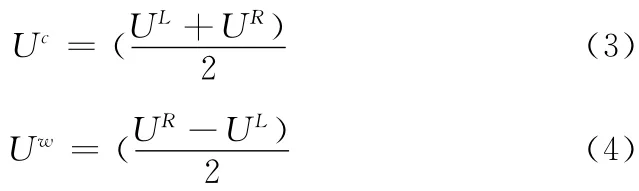
1.2 超椭球凸集模型

非概率集合理论模型是研究有界不确定性优化的数学方法和理论，主要分为两类［8，9］：一类基于凸模型优化理论，另一类基于区间数优化理论 （凸模型的一种特例）。本文基于凸模型理论，采用超椭球凸集模型［8，9］描述区间向量的不确定性信息。记m 维区间向量U ＝［u1，u2，…，um］∈I（Rm），则区间向量的不确定性信息可采用一个多维的超椭球凸集EU来量化

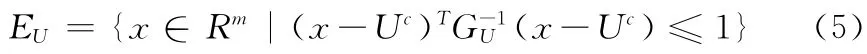
式 （5）中，GU表示超椭球凸集模型的特征矩阵，是一个m×m 阶的正定矩阵

2 区间不确定性超球支持向量机

2.1 IUHSVM 数学模型

针对区间不确定数据分类问题，每个样本表现为区间向量形式，简称区间样本。本文结合超椭球凸集模型，提出区间不确定性超球支持向量机分类方法 （IUHSVM）。与传统的超球支持向量机相似，IUHSVM 的分类策略如下：将每一类区间样本的超椭球凸集用最小包围球界定 （超球体），并通过各超球判断某个样本是否属于该类。

支持向量机通过引入核函数，将输入变量xi从样本空间映射到高维特征空间中构造最优超平面，解决了非线性数据的分类问题。

假设从样本空间到高维特征空间H 的映射为

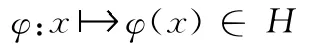
则核函数与内积运算相应表示为

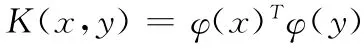
样本空间是特征空间的一个特例，不失一般性，本文直接给出区间不确定性数据在特征空间中的分类方法：

对于m 维属性区间不确定性样本集：Xi，i＝1，2，…l，Xi∈I（Rm）。IUHSVM 模型的最优超平面可以通过求解下面的不确定性约束规划问题得到

式中：a——球心；R——球半径；ξ——松弛因子；C——惩罚因子，用于控制模型训练精度和泛化性能的平衡；xi——区间样本范围内的不确定向量；EXi——区间样本的超椭球凸集，表示样本的不确定域。

问题 （6）是不确定性凸模型优化问题，通常采用Elishakoff提出的基于 “最差情况”处理的不确定优化方法［8］求解，则问题 （6）可转化为确定性约束规划问题

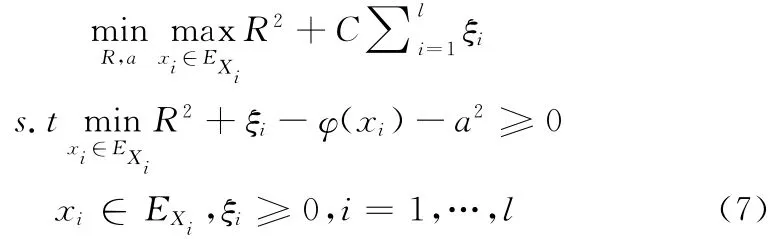
问题 （7）是一个两层嵌套的凸模型优化问题［8］，外层优化用于设计向量寻优，内层优化用于求取不确定性目标函数和约束在不确定域的最不利响应。

2.2 IUHSVM 模型的求解方案设计

目前，针对嵌套凸模型优化求解方法在理论和算法研究上还不完善，仍未发展出适应性较强的高效率通用求解算法。如文献 ［10］将凸集机会约束规划转化为二阶锥规划，导致大量的冗余变量，计算效率极低。为了降低嵌套凸模型优化求解算法的计算复杂度，通常根据问题特殊结构设计求解方法，如通过分解技术［8，15，16］将两层嵌套优化问题转转化为上下两层子优化交替迭代寻优求解的问题，则问题 （7）可转为形式如下：

上层优化问题

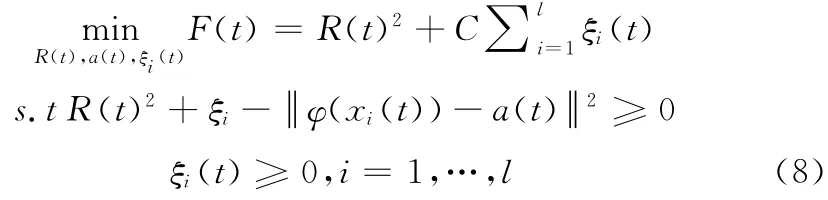
下层优化问题

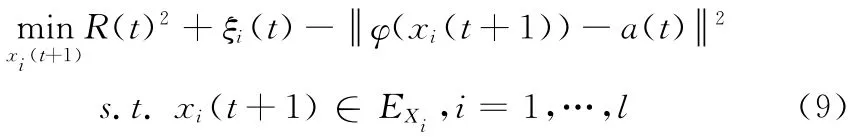
问题 （8）和问题 （9）中，t表示迭代的次数。其中，问题 （8）是常规形式的球结构支持向量机，可以使用其对偶问题求解

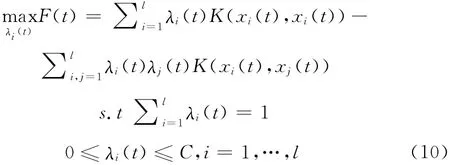
此时，求解问题 （7）等价于通过对子优化问题 （9）和问题 （10）的交替迭代求解，直至收敛得到的最优解。非线性凸集规划直接求解计算复杂度大，通常通过泰勒展开法，根据凸集的特殊结构，求解其线性近似规划问题［15，16］，从而得到近似最优解。问题 （9）是满足超椭球凸结构的非线性凸集规划，因此可以直接通过泰勒展开的线性近似问题推导得到其不确定量xi（t＋1）的近似最优解。下面给出IUHSVM 算法模型中下层优化问题中的不确定量xi（t＋1）的求解方法：

核函数K（x，y）＝φ（x）Tφ（y）包含两个参数x和y，当固定其中一个参数时，核函数可以被视为以另一个参数为自变量的函数。例如：固定y，则K（x，y）可以被视为以x为自变量的函数。此时，核函数关于x 的一阶泰勒展开式可表示为

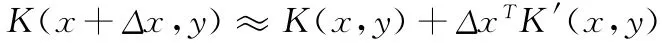
其中，K′（x，y）表示核函数在y处关于x 的偏导数。IUHSVM 算法中下层最优问题 （9）的求解方法如下：

定理1 在IUHSVM 算法中，下层优化问题 （9）的最优解xi（t＋1）是

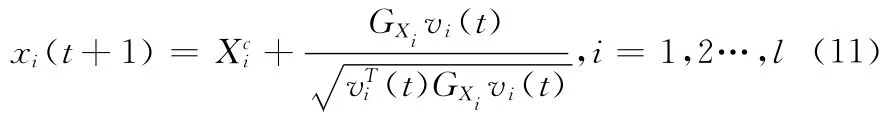
证明：在问题 （9）中，R（t），a（t）为已知，则问题 （9）等价于下面问题

不确定量可用区间样本均值和偏移量表示

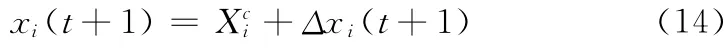
将式 （14）带入问题 （13）的目标函数，并用泰勒公式展开得

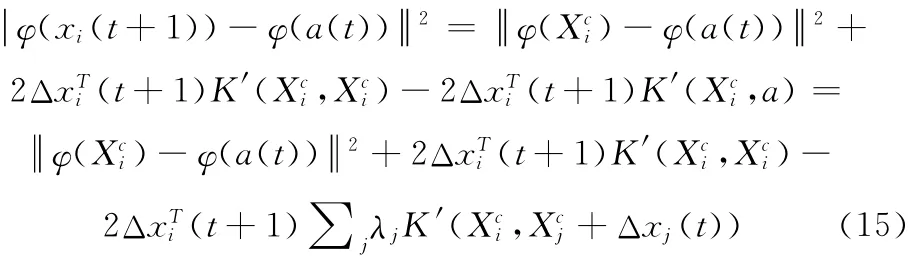
由题设条件可知， φ（Xci）－φ（a（t））2为常数，将式（12）带入式 （15），并化简，问题 （13）等价于下面的问题

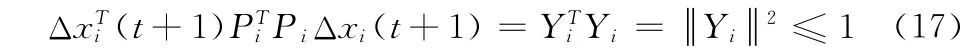
由式 （17） 和 Cauchy－Schwarz 不等式可知， 当取得最大值时，向量Yi与同方向且，令

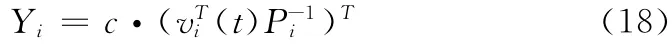
其中，c为正常量系数，其值越大，问题 （16）的目标值越大，将式 （18）带入式 （17）中，得

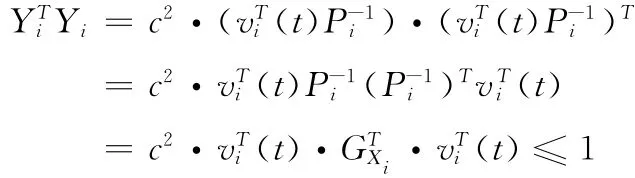
因此可知，当c取最大值时，有

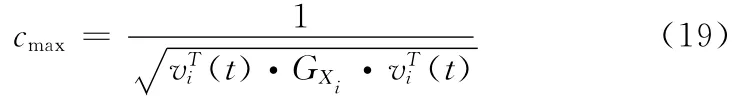
所以，问题 （16）的最优解为

因此，下层优化问题 （9）的最优解

定理1得证。

IUHSVM 求解算法的基本流程如下所示：

步骤1 初始化

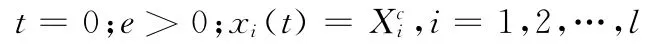
步骤2 计算上层优化问题：带入｛xi（t）｜i＝1，2，…，l｝，求解问题 （10）（当t＞0时，设置搜索初值为λi（t－1），i＝1，2，…，l），得到λi（t），i＝1，2，…，l，并计算：R（t），a（t），ξi（t）；

步骤3 算法收敛检验：若‖F（t）‖≤e：算法结束，输出R（t），a（t），xi（t）；否则转至步骤4；

步骤4 计算下层优化问题，迭代更新：将a（t）带入式 （11）、式 （12），计算下层优化的近似最优解

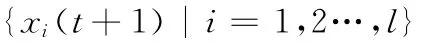
令t＝t＋1，转至步骤2，直至满足收敛条件。

预测分类策略为：分别计算未知类别样本到各超球中心距离与该超球半径的比值，并将样本划分到比值最小的超球所对应的类别。

3 实验及结果

实验环境为Windows 7 操作系统、lntel奔腾E5400（2.7GHz）双核处理器、2GB内存。实验中的算法都是基于MATLAB R2010a平台开发。

3.1 实验数据

本文的所有实验数据均来自UCI标准数据库（http：／／archive.ics.uci.edu／ml／datasets.html）。表1中列出了实验所用数据集。由于目前尚未有公开的不确定性数集，针对不确定性数据的实验都需在确定数据集上引入不确定性信息。方法如下：

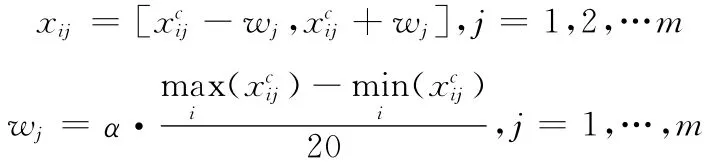
其中，maix与miin的差值表示数据集第j维属性分布区间的大小，α控制实验所添加噪声大小范围的参数。

实验数据集见表1。

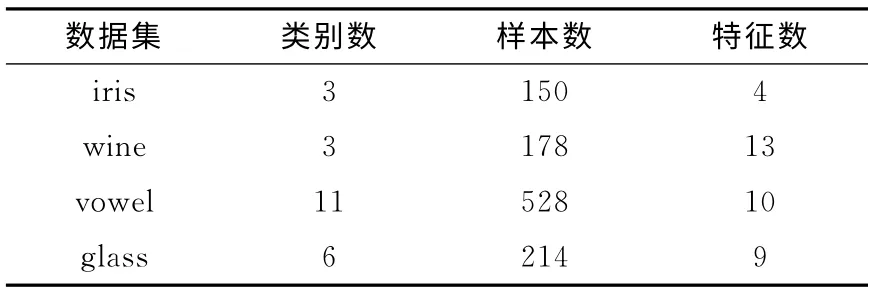
表1 实验数据集

3.2 实验设置

为了分析IUHSVM 算法的分类精度及训练速度，本文进行了3组仿真实验。

3.2.1 实验一

实验一为验证IUHSVM 方法对区间不确定性信息的抗干扰能力，实验采用iris、wine、vowel和glass这4组数据集，先测试SVM 和HSVM 方法对精确数据集的分类精度作为比较对象，接着对实验数据集添加区间不确定性信息，验证IUHSVM 算法对区间不确定性数据的分类精度，并与针对区间不确定性数据的朴素贝叶斯方法 （NBU1［5］和FBC［6］）的分类精度进行了比较。由于基于随机理论的不确定性支持向量机方法［8，10］在数据的获取、表示及描述模型上与非概率不确定性数据有较大区别，所以实验并未与该类方法进行比较。实验采用径向基核函数

实验参数设定：实验数据集的每个样本随机设定区间不确定参数α∈［0.5，2］；惩罚参数取值范围为C ＝［2－1，20，…，24］；径向基参数的取值范围为σ＝［2－1，20，…，24］。并记录不同参数组合下最好的分类结果。为验证算法的稳定性，实验采用5折交叉验证 （5－fold cross validation）估计算法分类精度：对每一数据集，将数据集随机分为5组，轮流选择其中一组作为测试集，其它4组作为训练集，取5次结果的均值作为最终估计精度，实验结果见表2。

表2 不同算法的分类准确度／%

从表2中可以看出，对添加不确定性信息的数据集分类的IUHSVM 方法与对精确数据集分类的HSVM 方法分类精度较接近，这表明IUHSVM 方法对非概率不确定性噪声具有一定的抗干扰能力；同不确定性数据的朴素贝叶斯方法相比，IUHSVM 方法具有较优的分类精度和鲁棒性，针对vowel和glass数据集，IUHSVM 方法的分类精度比FBC方法分别高16.9%和6.2%；比NBU1分别高29.7%和9.4%。实验结果表明：IUHSVM 算法具有一定克服不确定性噪声的能力，且具有良好的分类精度和鲁棒性，适用于区间不确定性数据的分类问题。

3.2.2 实验二

实验二测试IUHSVM 算法在不同迭代次数下目标函数的收敛情况，实验数据集同实验一，实验结果如图1所示。

在图1中，各曲线分别表示构造某一类别超球面时，迭代次数与目标函数的关系 （如iris数据集有3个类别的数据，因此有3条曲线）。从图中可以看出，4个数据集的目标函数全都在第2次迭代时波动较大，之后趋于稳定 （部分曲线处于微小波动状态，其原因是上下两层子规划的交替迭代求解方法属于非光滑优化算法［18］）。实验数据集几乎都在5次内到达收敛条件，因此可通过设置较小的最大迭代次数来控制算法的计算复杂度。实验结果表明，基于超球支持向量机的IUHSVM 方法具有快速的迭代收敛速度，计算效率高。

3.2.3 实验三

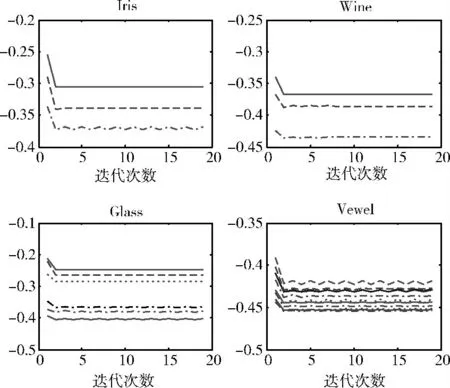
图1 迭代次数与目标函数收敛情况

实验三测试IUHSVM 算法在执行时间上的性能，并与针对精确数据且采用主流多分类的1v1－SVM、1vr－SVM 方法进行了比较。实验采用Vowel数据集，包含了528个样本，共有11个类别，样本的属性维数为10。实验分别选取Vowel中的m 类数据进行分类，并记录不同类别数下的训练速度，实验结果如图2所示。

图2 样本类别数与训练时间关系

从图2可以看出，随着样本类别的增加，1v1－SVM 的训练时间急剧增加，而1vr－SVM 和IUHSVM 方法的训练时间成正比增加。IUHSVM 方法采用迭代策略，但即使在最大迭代次数分别为5、10、20的情况下，执行时间都低于其它两种方法，尤其是设置最大迭代次数为5时 （对应图2中最下面的线段），执行时间的优势极为明显。

实验结果表明：针对不确定性数据，即使IUHSVM 方法采用了迭代策略，但其执行时间要远小于针对精确数据的标准SVM 主流多分类器的执行时间，即球结构支持向量机具有远小于标准结构SVM 的主流多分类器的计算代价，适合不确定性数据分类 （往往具有高于精确数据的计算代价）的性能要求。

4 结束语

数据分类的工程应用中，常遇到区间形式的不确定性数据，而支持向量机是针对确定数据提出的二分类方法，不能直接用于不确定性数据的分类问题。因此，提出了一种面向区间不确定性数据的分类方法IUHSVM。该方法基于球结构支持向量机，具有远高于基于标准结构支持向量机的主流多分类器方法的计算效率。仿真结果表明：针对区间不确定性数据，同基于朴素贝叶斯的FBC 和NBU1方法相比，IUHSVM 算法具有较优的分类精度和鲁棒性，适用于多类别的不确定性数据分类问题。

［1］Aggarwal CC，Yu PS.A survey of uncertain data algorithms and applications ［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21 （5）：609－623.

［2］ZHOU Aoying，JIN Cheqing，WANG Guoren，et al.A survey on the management of uncertain data［J］.Chinese Journal of Computers，2009，32 （1）：1－16 （in Chinese）. ［周傲英，金澈清，王国仁，等.不确定性数据管理技术研究综述 ［J］.计算机学报，2009，32 （1）：1－16.］

［3］REN Shijin.Interval number－based uncertain data mining and its applications ［D］.Hangzhou：Zhejiang University，2006（in Chinese）.［任世锦.基于区间数的不确定性数据挖掘及其应用研究 ［D］.杭州：浙江大学，2006.］

［4］Tsang S，Kao B，Yip KY，et al.Decision trees for uncertain data［J］.IEEE Transactions on Knowledge and Data Engineering，2011，23 （1）：64－78.

［5］REN Jiangtao，LEE SD，CHEN Xialu，et al.Naive bayes classification of uncertain data［C］／／Ninth IEEE International Conference on Data Mining，2009：944－949.

［6］QIN Biao，XIA Yuni，WANG Shan，et al.A novel Bayesian classification for uncertain data ［J］.Knowledge－Based Systems，2011，24 （8）：1151－1158.

［7］QIN Biao，XIA Yuni，Prabhakar S，et al.A rule－based classification algorithm for uncertain data ［C］／／IEEE 25th International Conference on Data Engineering，2009：1633－1640.

［8］REN Zhiping，WANG Xiaojun，XU Menghui.Engineering structure uncertainty optimization design technology ［M］.Beijing：Science Press，2013 （in Chinese）. ［邱志平，王晓军，许孟晖.工程结构不确定性优化设计技术 ［M］.北京：科学出版社，2013.］

［9］JIANG Chao.Theories and algorithms of uncertain optimization based on interval［D］.Changsha：Hunan University，2008（in Chinese）. ［姜潮.基于区间的不确定性优化理论与算法［D］.长沙：湖南大学，2008.］

［10］YANG Jianqiang.Classification under input uncertainty with support vector machines ［D］.Southampton：University of Southampton，2009.

［11］DENG Shifei，QI Bingjuan，TAN Yanhong.An overview on theory and algorithm of support vector machine ［J］.Journal of University of Electronic Science and Technology of china，2011，40 （1）：2－10 （in Chinese）.［邓世飞，齐丙娟，谭艳红.支持向量机理论与算法研究综述 ［J］.电子科技大学，2011，40 （1）：2－10.］.

［12］AI Qing，QIN Yuping，LI Yingchun.Multi－subjects text classification algorithm based on hyper－sphere support vector machines［J］.Computer Engineering and Design，2010，31（10）：2272－2275 （in Chinese）. ［艾青，秦玉平，李迎春.基于超球支持向量机的多主题文本分类算法 ［J］.计算机工程与设计，2010，31 （10）：2272－2275.］

［13］LI Weixiang，LI Bangyi.Research in multiple classifications for interval number based on SVDD ［J］.Journal of Systems Science and Mathematical Sciences，2012，32 （3）：319－326（in Chinese）.［李为相，李帮义.一种基于支持向量域描述的区间数分类 ［J］.系统科学与数学，2012，32 （3）：319－326.］

［14］ZHAO Yinggang，CHEN Qi，HE Qingming.Fast learning algorithm for support vector domain description ［J］.Chinese Journal of Scientific Instrucment，2008 （z1）：798－800 （in Chinese）.［赵英刚，陈奇，何钦铭.基于支持向量域数据描述的快速学习算法［J］.仪器仪表学报，2008 （z1）：798－800.］

［15］Pistikopoulos EN，Dominguez L，Panos C，et al.Theoretical and algorithmic advances in multi－parametric programming and control［J］.Computational Management Science，2012，9 （2）：183－203.

［16］Suvrit Sra，Sebastian Nowozin，Stephen J Wright.Optimization for machine learning ［M］.Cambridge，MA：Mit Press，2012.