基于子空间的正交匹配追踪算法

【信息科学与控制工程】

基于子空间的正交匹配追踪算法

李强云， 武昕伟

(陆军军官学院，合肥230031)

摘要：压缩感知理论的提出，给信号处理和信息获取领域带来了划时代的发展。传统重构压缩算法大多都有迭代次数多、运算效率不高且重构效率低等问题。针对该问题，提出了一种根据子空间回溯思想重构出原始信号，并证明了该算法的有效性和重要2个特点：引入回溯思想，重构概率高；计算复杂度低。通过仿真实验与传统的正交跟踪(OMP)算法和子空间(SP)算法进行相关参数比较，验证了该算法在稀疏信号重构研究中具有重要意义。

关键词：压缩感知；子空间；OMP算法；SP算法

收稿日期：2014-12-05

作者简介：李强云,男，硕士研究生，主要从事雷达成像技术研究;武昕伟，男，硕士生导师，副教授，主要从事雷达成像技术和信号处理技术研究。

doi:10.11809/scbgxb2015.06.028

中图分类号：TN911

文章编号：1006-0707(2015)06-0113-05

本文引用格式：李强云， 武昕伟.基于子空间的正交匹配追踪算法[J].四川兵工学报，2015(6):113-116.

Citation format:LI Qiang-yun, WU Xin-wei.Research of Orthogonal Matching Pursuit Algorithm on the Base of Subspace[J].Journal of Sichuan Ordnance,2015(6):113-116.

Research of Orthogonal Matching Pursuit Algorithm

on the Base of Subspace

LI Qiang-yun, WU Xin-wei

(Academy of Army Officer of PLA, Hefei 230031, China)

Abstract:As the theory of compressed sensing was proposed, it had brought a landmark to the development of signal processing and obtaining information domains. Most traditional compressed reconstruction algorithms had some problems, such as the high iterations, low efficiency of operation and low recovery probability and so on. This paper had proposed backtracking idea to recovery original signal on the base of subspace, which also proved its availability and two important characteristics: firstly, high recovery probability because of drawing into backtracking idea, and secondly, the low computational complexity. This paper had compared parameters with traditional Orthogonal Matching Pursuit algorithm and Subspace Pursuit algorithm, and proved its significant importance in the sparse signal recovery domain.

Key words: compressed sensing; subspace; OMP algorithm; SP algorithm

压缩感知(compressed sensing,CS)，又叫压缩传感，由Candes、Donho等[1,2]在2006年提出的，突破了传统奈奎斯特采样定理的限制，是一种全新信号处理和信息获取理论。压缩重构算法是压缩感知理论的关键部分，目前，比较成熟的算法有：BP(Basis Pursuit)算法、OMP(orthogonal matching pursuit)算法、GP(gradient pursuit)算法等等。大多数这些算法在每次迭代时没有更新信号支撑集，若第一次找到的信号支撑集错误或误差较大，将导致信号重构失败，重构概率低。本研究引入子空间回溯思想，在下一次迭代时，更新上一次找到的信号支撑集，最后直到残差为零，通过伪逆运算重构出原始信号。

1压缩感知理论

对于稀疏信号重构问题，文献[3,4]中提出了OMP算法和SP算法，下面予以简单介绍2种算法的主要步骤。

1.1OMP算法的主要步骤

1) Input parameters:Φ,y,K

2) Initialize:ro=y,Λ0=∅，t=1

3) Find:λt=argmax|〈rt-1,φj〉|, (j=1,2,…,N)

Update support:Λt=Λt-1∪{λt}

Judge whethert>K, if satisfied then end,if not back to findλt

1.2SP算法的主要步骤

1) Input parameters:Φ,y,K

2) Initialize:T0={corresponding to the largest magnitude entries in the vectorΦ*y}

3) forl iteration，

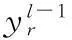
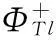
Update:Tl=max(xp)

从以上2种算法主要步骤可以看出：① OMP算法在找到信号支撑集便不再更新，若找到的支撑集错误或误差较大将导致重构效率低；② SP算法中没有引入正交思想进行处理，且对于稀疏度为K的信号，至少需要K次迭代才能重构出原始信号，重构效率不高。

2基于子空间的OMP算法描述

针对以上2种算法的缺点，本文引入文献[3,4]中的子空间回溯思想，提出基于子空间的OMP算法，该算法在每次迭代时需要找到信号支撑集(值不为0的位置)的估计，在下一次迭代时修正上一次找到的信号支撑集，直到残差小于指定的阈值时找到的信号支撑集，最后重构出原信号。具体算法框图如图1所示。

图1　OMP算法框图

2.1算法步骤

基于子空间的OMP算法主要步骤如下：

1) Input parameters Phi,y,K.

2) Initializero=y,T0=∅，l=1

3) forliteration，choose the bestIltorl-1

Il=argmax(mean(|ΦT[I]rl-1|))

ComputeTl=Tl-1∪Il

Judge whetherrl<δ, if satisfied then end,if notl=l+1

2.2复杂度分析

本研究算法的计算复杂度主要集中在相关最大化(Correlation Maximization，EM)运算(上述步骤求Il)中，即测量矩阵与残差之间的乘积。因此为确定该算法的复杂度，只需确定精确重构需要的迭代次数。现对0-1二值无噪信号进行本算法仿真实验，N=256，算法运行100次，指定阈值δ=10-4，算法平均迭代次数与稀疏度K之间的关系如图2所示。实验在Matlab R2010a环境下完成，CPU为G640，2.80 GHz，内存为1.90 GB，后面仿真实验均在以上条件下进行，不再重复说明。

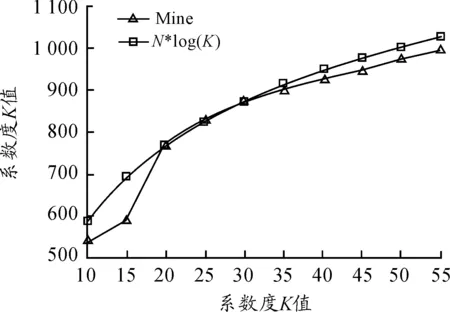
图2　本文算法迭代次数与稀疏度 K关系对比

从图2可以看出：本研究算法迭代次数与稀疏度K之间的关系近似表示为O(NlogK)(实际上是小于O(NlogK))。算法在每次迭代时需进行CM运算需要m*N次乘积，则本研究算法的复杂度可以控制在O(mNlogK)以内。文献[3,4]中已证明OMP算法、SP算法的运算复杂度均在O(mNK)左右。所以在复杂度方面，算法运算复杂度均低于上面2种算法，从理论分析上验证了本文算法运算复杂度低特点。

2.3算法重构源信号的充分条件

定理：若x为K稀疏的信号，则本文算法能够重构信号x的充分条件为

(1)

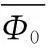
(2)

式中：ρ为矩阵Φ的谱半径；Φ[l,r]为矩阵Φ中第(l,r)个元素。在证明本定理之前，先给出以下必要的定义及引理。

定义：向量x的混合l2/lp范数

(3)

若对于矩阵Φ，Φ∈Rm×N，矩阵Φ的混合范数为

(4)

引理：若矩阵Φ为m×N大小，Φ[l,r]为矩阵Φ中第(l,r)个元素，则有下式成立[5]：

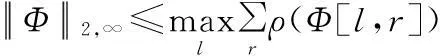
(5)

(6)

特别地，ρr(Φ)=ρc(ΦT)。

定理的证明：根据前面已经介绍的内容可以看出，该算法的重点是找到正确的信号支撑集，然后通过伪逆运算重构源信号x，所以若算法能重构x，则与2.1节中第3步骤中最大相关处理时等价，即每次迭代时都能找到部分正确的信号支撑集，如式(7)所示

(7)

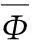
图3　残差 r l与两空间距离对比

由于

(8)

则有

(9)

根据引理的式(5)有

(10)

(11)

最终可得

(12)

以上便完成了对定理的证明，在此还有2点补充说明：

1) 在实际的数据传输过程中，若原始信号x的部分先验条件已知，如支撑集位置等，可以通过计算验证测量矩阵Φ是否满足本研究算法的充分条件。

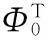
(13)

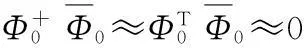
2.4重构概率分析

本研究算法在OMP算法的基础上利用子空间的回溯思想，即在每次进行第l+1迭代时，都要更新第l次迭代信号支撑集的估计值，而OMP算法找到信号支撑集后便不再更新，若找到的支撑集误差较大或错误将导致重构信号失败[8-10]；相比SP算法，又利用了OMP正交的优点，可以很好地重构出原始信号，综上所述可看出该算法较其他2种算法均有一定的改进，重构概率也相应得到提高[11-13]。

3仿真实验及分析

为通过仿真实验验证该算法可以有效提高重构概率和减少运算复杂度，首先对0-1的二值信号进行仿真实验，并与传统的OMP算法和SP算法进行性能对比。原始信号为随机产生的0-1二值无噪信号，N=256，源信号稀疏度K=20，对每种算法运行100次，指定阈值δ=10-4，测量矩阵均采用随机高斯矩阵[6]。当测量值M=128时，算法运行结果如图4所示，当测量值M变化时，算法重构概率与测量值M关系如图5所示，左边为无噪情况下的结果，右边为有噪声情况下的结果，其均值为零，偏方差为0.01的高斯信号。

图2和图4的结果验证了该算法可以实现0-1稀疏信号的重构，并且重构概率非常高，与传统OMP算法和SP算法相比，不论有无噪声，其重构概率结果都比前两者要好。当以上算法重构概率大于0.95时，算法运行时间和测量误差结果如表1所示。

表1　算法运行时间、测量误差与测量值M的关系

图4　M=128时0-1信号算法运行结果

图5　0-1信号仿真结果对比

表1可以看出：本算法与OMP算法、SP算法相比，在测量值M相同情况下，算法运行时间和测量误差均小于后两者测量值，可见该算法在OMP算法引入回溯思想、在SP算法上利用正交的思想可以有效减少在寻找信号支撑集错误的概率，从而提高信号重构概率，验证了该算法优于OMP算法和SP算法。

4结束语

提出了在子空间回溯思想的基础上运用OMP信号重构算法，在下一次迭代时，更新上一次找到的信号支撑集，最后直到残差小于指定阈值，通过伪逆运算重构出原始信号。也证明了该算法重构信号的充分条件，说明了该算法的普遍性。通过理论和实验分析了本算法运算复杂度可以控制在O(mNlogK)以内。通过将0-1信号在无噪、有噪情况下分别进行仿真和二维lena图像信号仿真实验，验证了本算法的有效性，可以很好地降低信号重构时间、减少误差和提高信号重构概率，对于信号处理有深远意义。

参考文献：

[1]DonohoD.Compressedsensing[J].IEEETrans.Inf.Theory,2006,52(4):1289-1306.

[2]CandèsE,RombergJ,TaoT.Robustuncertaintyprinciples:Exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETrans.Inf.Theory,2006,52(2):489-509.

[3]TroppJA，GilbertAC.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETrans.Inf.Theory,2007,53(12):4655-4666.

[4]DaiW,MilenkovicO.Subspacepursuitforcompressivesensingsignalreconstruction[J].IEEETransonInformationTheory,2009,55(5):2230-2249.

[5]BarniukRG,CevherV,DuarteMF,etal.Model-basedcompressivesensing[J].IEEETransonInformationTheory,2010,56(4):1982-2001.

[6]RudelsonM,VershyninR.OnsparsereconstructionfromFourierandGaussianmeasurements[J].Commun.PureAppl.Math.,2008,61(8):1025-1045.

[7]石光明,刘丹华,高大华,等.压缩感知理论及研究发展[J].电子学报，2009,37(5):1070-1081.

[8]付宁,曹离然,鹏喜元.基于子空间的块稀疏信号压缩感知重构算法[J].电子学报,2011,39(11):2338-2342.

[9]EldarYC,KuppingerP,BolcskeiH.Compressedsensingofblock-sparsesignals:uncertaintyrelationsandefficientrecovery[J].IEEETransonSignalProcessing,2010,58(6):3042-3054.

[10]KezhiLi,LuGan,CongLing.ConvolutionalCompressedSensingUsingDeterministicSequences[J].IEEETransonSignalProcessing,2013,61(3):740-752.

[11]WenbiaoTian,GuoshengRui.BlindSparsityWeakSubspacePursuitforCompressedSensing[J].TheInstitutionofEngineeringandTechnology,2013,49(6):369 - 370.

[12]HansenTL,JohansenDH,JorgensenPB,etal.CompressedSensingwithRankDeficientDictionaries[J].Globecom2012SignalProcessingforCommunicationsSympium,2012:3594-3599.

[13]AmbatSK,SaikatChatterjee,HariKVS.FurionofAlgorithemforCompressedSensing[J].IEEETransonSignalProcessing,2013,61(14):3699-3704.

(责任编辑杨继森)