折痕识别中的李群核研究

【信息科学与控制工程】

折痕识别中的李群核研究

岳洪伟1,2,郑永敏2,廖伟2,王克强2

(1.五邑大学 信息工程学院，广东 江门529020； 2.仲恺农业工程学院 自动化学院,广州510225)

摘要：针对毛杆折痕难以检测问题，提出了一种基于均值协方差描述子和李群核的折痕识别方法。均值协方差描述子是目标图像的特征模型，可以将各种类型特征自然地融入统一的特征模型中，实现了基于多特征的折痕识别。由于构建的均值协方差矩阵不具有对称结构，首先证明其具有李群结构，并赋予具有双不变度量性质的Log-Euclidean黎曼度量。推导了黎曼流形中内积空间的度量形式，给出李群核函数表达式，并以此设计了基于李群核的识别算法。实验结果表明均值协方差矩阵比协方差矩阵更适合构建折痕特征；而且该算法具有更好的线性可分性。

关键词：羽毛杆折痕；均值协方差描述子；李群核

作者简介：岳洪伟(1979—)，男，博士，讲师，主要从事图像处理、模式识别研究。

doi:10.11809/scbgxb2015.06.021

中图分类号：TL361

文章编号：1006-0707(2015)06-0082-05

本文引用格式：岳洪伟,郑永敏,廖伟,等.折痕识别中的李群核研究[J].四川兵工学报，2015(6):82-86.

Citationformat:YUEHong-wei,ZHENGYong-min,LIAOWei,etal.ResearchonLieGroupKernelinFeatherQuillCreaseRecognition[J].JournalofSichuanOrdnance,2015(6):82-86.

ResearchonLieGroupKernelinFeatherQuillCreaseRecognition

YUEHong-wei1, 2,ZHENGYong-min2, LIAO Wei2, WANG Ke-qiang2

(1.SchoolofInformationEngineering,WuyiUniversity,Jiangmen529020,China; 2.CollegeofAutomation,

ZhongkaiUniversityofAgricultureandEngineering,Guangzhou510225,China)

Abstract:Aiming at the detection difficult problem of feather quill crease, an algorithm for feather quill crease recognition was proposed based on mean covariance descriptor and manifold kernel. Mean region covariance descriptor was employed to represent the object which enables efficient fusion of different types of features and modalities into a unified feature model, used as multi-cue integration for crease recognition.Due to that mean covariance matrix is not symmetric, we first proved that mean covariance matrix forms a Lie group. Based on Lie group theory, geodesic distance can be computed between two group elements in the Log-Euclidean framework with double invariance properties. Then this article designed recognition algorithm based on Lie group kernel with metrics of inner product space and manifold kernel function expression which were deduced. The experiment section gave classification comparison through the algorithm in separate methods using mean covariance matrix and covariance matrix. The results show that mean covariance matrix is more suitable for constructing feather quill crease features and the proposed algorithm has better linear distribution.

Keywords:featherquillcrease;meancovariancedescriptor;Liegroupkernel

生产羽毛球所使用的鸭毛或鹅毛毛片直接影响着羽毛球质量和经济效益。如果羽毛杆(以下简称“毛杆”)出现折痕，表面角质层受损会损害羽毛球耐打度。我国羽毛球产量占世界总产量90%以上，折痕检测还是依靠人工完成，存在劳动强度大，分拣质量不稳定等问题。由于毛杆宽度在1mm到3mm之间，折痕大致与毛杆法线平行；其细长结构和具有的拱度弯度都以及毛杆分割残余绒毛都对折痕特征识别造成干扰，这使得针对具体对象的处理方法[1-3]无法有效区分折痕与非折痕。目前课题组也对此做了一定的研究工作[4-6]。

近年来流形作为欧氏空间的推广在图像解释分析上有着广泛应用[7-10]。流形可以在局部建立欧氏空间的微分同胚，具有局部平滑性和线性结构，流形上每点都存在一个邻域可以用局部坐标系来刻画。Pennec等提出仿射不变度量研究图像匹配问题[11]。Caseiro等则基于正定对称矩阵构建改进的李群结构[12]，赋予具有双不变性质的Log-Euclidean度量进而完成目标分割。

由于流形在局部意义下能获得近似的全局线性结构，在流形空间对图像进行处理有利于获取数据的低维嵌入坐标，从而完成特征提取等任务。考虑到毛杆结构特性,本研究提出了均值协方差矩阵和李群核函数相结合的毛杆折痕识别方法。文献[12]中构建改进的李群结构是基于对称矩阵进行研究。由于均值协方差矩阵不具有对称结构，在赋予其新的乘法运算后，首先证明了其具有李群结构，再采用Log-Euclidean黎曼度量研究折痕特征识别问题；并在定义矩阵内积基础上推导出李群核函数，实现了特征空间到线性可分空间的映射，以此设计了基于李群核的折痕识别算法。

1均值协方差描述子和李群

1.1均值协方差描述子

假定I为待提取协方差特征的灰度图像，提取的特征F(x,y)=φφ(I,x,y)，式中函数φ指代一种映射，可以张成d维实空间。定义映射φ如下所示：

(1)

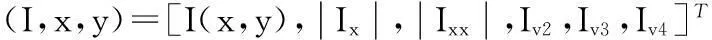
(2)

(3)

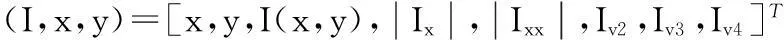
(4)

(5)

其中Cd=RRT，Cdμ为(d+1)×(d+1)的矩阵。该模型融合小波重构细节图像，灰度，梯度，均值向量参数等统计特性。

1.2矩阵李群

定义1设G是一个非空集合，如果

1) G是一个群；

2) G是r维光滑流形;

文献[12]提出对任意正定对称矩阵S1,S2∈Sym+(n)，通过在Sym+(n)上赋予新运算：S1⊗S2=exp(logS1+logS2)，则可以证明(Sym+,⊗)是李群。由于本研究的Cdμ∉Sym+(n) 不是对称矩阵，若对∀S1,S2∈Cdμ，下面证明(Cdμ,⊗) 是李群：

证明：该证明分两步，首先证明其具有群结构，再证明是李群。

1) 首先证明其具有群结构

① 任意∀S1,S2∈Cdμ，∃S1⊗S2∈Cdμ；

② ∀S1,S2,S3∈Cdμ，∃(S1⊗S2)⊗S3=S1⊗(S2⊗S3)；

④ ∀S∈Cdμ,∃S-1∈Cdμ；

所以(Cdμ，⊗)构成一个群。

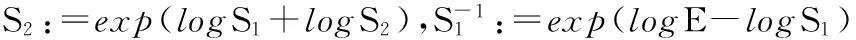
从李群定义可知：李群是一个具有群结构的流形,在其上可以赋予Log-Euclidean黎曼度量。于是，两点间的距离公式可表示为

(6)

设xi是正定对称矩阵，则其黎曼均值存在且唯一，称为Log-Euclidean均值为

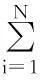
(7)

2基于李群核的识别算法

2.1李群核函数

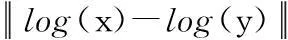
指数RBF核函数：

K(x,y)=e-a(tr([log(y)-log(x)]2)) a>0

(8)

双曲正切核函数：

(9)

线性核函数：

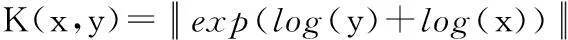
(10)

Sigmoid核函数：

(11)

2.2识别算法原理

(12)

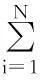
(13)

(14)

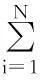
步骤1求出每类均值协方差矩阵样本的Log-Euclidean均值μi；

步骤2选择具体李群核函数，计算Kb、Kw，a；

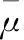
3实验

本研究所使用的实验样本是以台湾鸭毛为原材料，通过面阵摄像机所获取。自制羽毛片采集系统实物照片如图1所示。实验样本库包含1 000个无折子图像，450个有折子图像。每个样本是26×20像素灰度图片。样本都进行了边缘舍弃以减少毛杆边缘噪声影响，图2为其部分折痕样本的显示效果。本实验中RBF核函数参数取值为2.21；双曲正切核函数取a=10-5，c=0；Sigmoid核函数取a=10-9。

图1　羽毛片采集系统

图2　部分折痕样本

对每个类别分别随机抽取50个作为训练样本，其余作为测试样本，测试5次并取其平均识别率作为实验结果。图3、图4使用该算法进行折痕识别，其中特征矩阵分别是Cdμ和Cd。其中纵坐标为样本识别率，横坐标为特征维数。实际生产中大部分毛杆是无折的，这就要求保证无折毛杆有着很高识别率基础上提高折痕毛杆的识别率。从图3可以看出线性核、双曲正切核和Sigmoid核有着很高的识别率，选择d=6，7时无折识别率均高于95%，无折识别率均高于80%。图4中只有指数RBF核函数有着较好的识别率，但是也低于图3的识别率。这说明构建特征采用的Cdμ比Cd更有利于折痕判别。

图3　均值协方差描述子结合李群核的分类结果

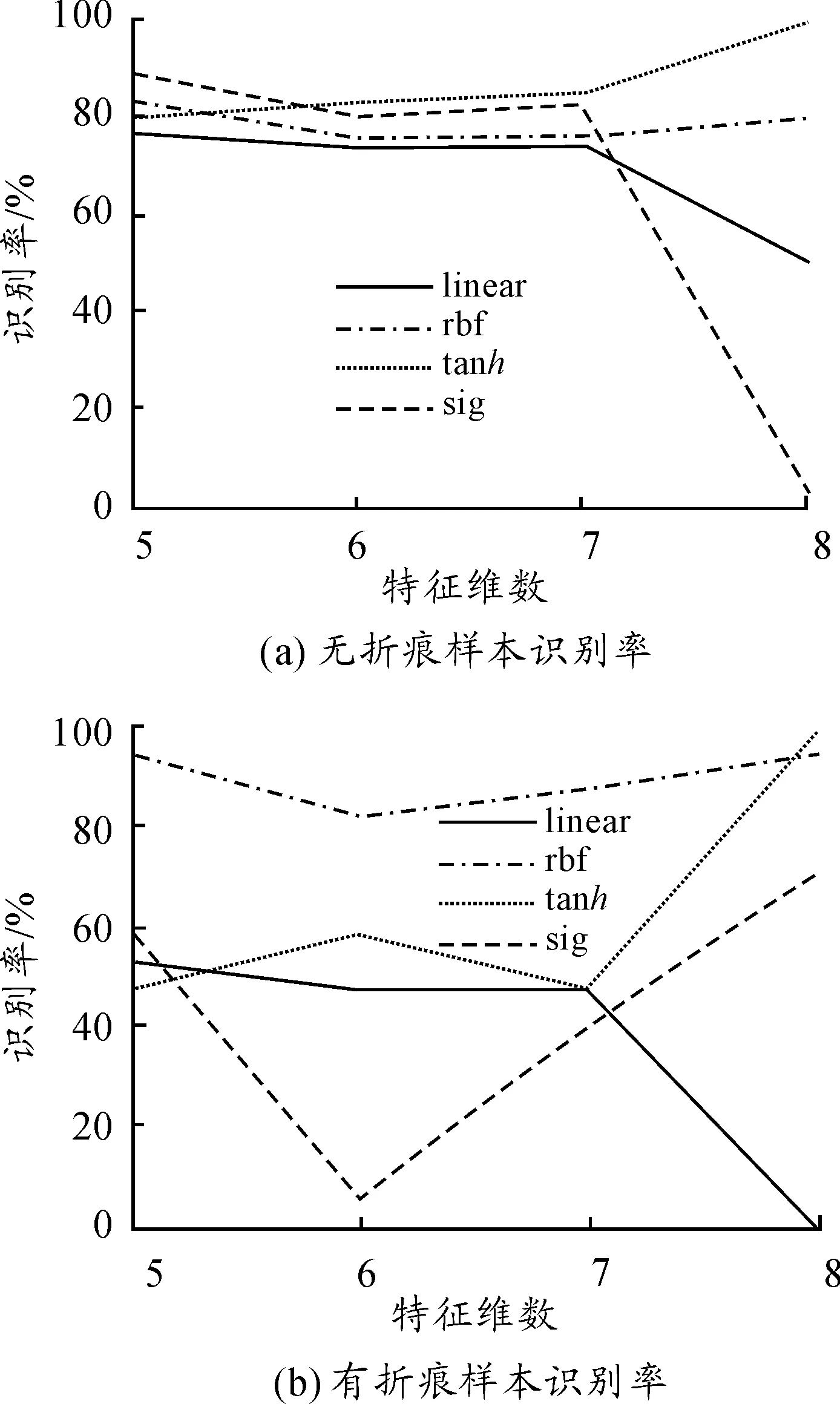
图4　协方差描述子结合李群核的分类结果

图5是李群核函数结合SVM算法对样本进行分类，特征矩阵为Cdμ。经图3与图5对比可以看出采用李群核的算法具有更好的线性可分性，而SVM算法无法有效对折痕与非折痕进行区分。例如Sigmoid函数虽然对有折识别率是100%,但是对无折识别率是0%。指数径向基函数在这3种方法中总体识别率比较一般。从以上3个图也可以看出，当d=8时发生识别率较大波动，这主要由于折痕位置具有随机性，特征矩阵包含的位置信息对折痕识别造成干扰。由于实际生产中无折痕羽毛杆占大部分，所以在选择核函数和d时应优先考虑无折识别率，这样可以减少误判。

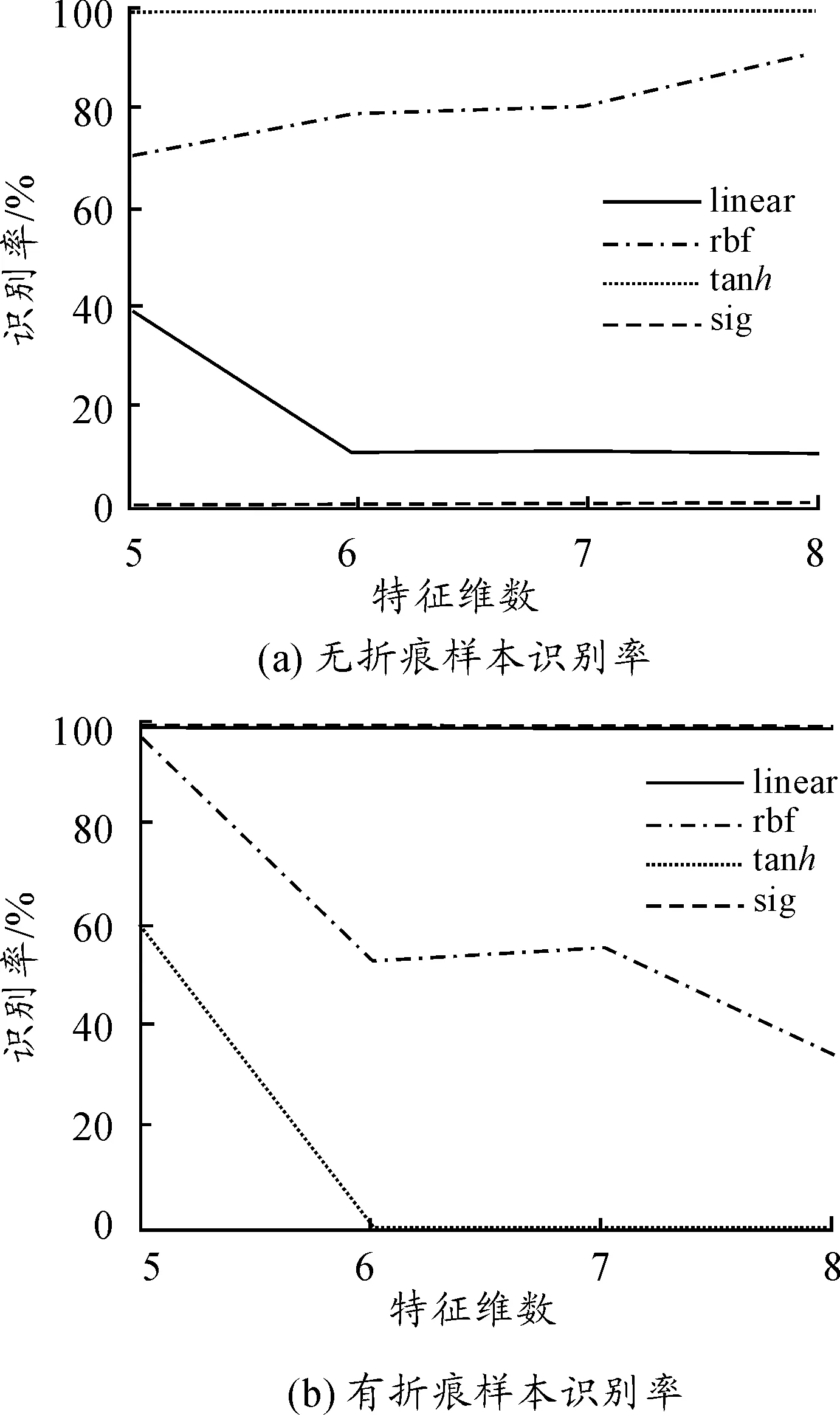
图5　均值协方差描述子结合 SVM算法分类结果

4结束语

由于目前羽毛球行业还处于人力密集型阶段，其中折痕判断完全依靠人工完成。而且羽毛片中大部分是无折，这就要求进行检测时优先考虑无折识别的准确率。采用均值协方差描述子，提出在流形上完成折痕特征分类识别的新方法。实验对比说明该算法的均值协方差矩阵融合小波重构细节图像、灰度、梯度、均值向量参数等统计特性，比协方差矩阵更适合用于描述折痕特征。实验对比结果也表明所提出的基于李群核的算法识别率也优于均值协方差矩阵结合SVM的识别率。通过实验可以看出，通过选择特征表达式可以使无折识别率超过95%，折痕识别率则达到80%以上。由于实测毛杆图像会不可避免地受到光照不均等影响，所以还需要在预处理方法上进一步研究以提高识别率。

参考文献：

[1]邵家鑫,都东,石涵,等.基于厚壁工件X射线实时成像的焊缝缺陷自动检测[J].清华大学学报:自然科学版,2013,53(2):150-154.

[2]龚芳,张学武,孙浩.基于独立分量分析和粒子群算法的太阳能电池表面缺陷红外热成像检测[J].光学学报,2012,32(4):169-177.

[3]姚明海,李洁,王宪保.基于RPCA的太阳能电池片表面缺陷检测[J].计算机学报,2013,36(9):1943-1952.

[4]YueHW.ResearchonFeatherQuillImageDenoising[J].ComputerModellingandNewTechnologies,2013,17(4):51-57.

[5]岳洪伟,汪仁煌,金迎迎,等.流形核与LPP相结合的毛杆折痕识别方法[J].光电工程,2014,41(2):47-52.

[6]HongweiYue,RenhuangWang,JinghuaZhang,etal.FusionofGrayandGradsInvariantMomentsforFeatherQuillCreaserecognition[C]//Proceedingsof2013IntelligentAutomationConference.SpringerBerlinHeidelberg,2013:121-128.

[7]TosatoD,SperaM,CristaniM,etal.Characterizinghumansonriemannianmanifolds[J].PatternAnalysisandMachineIntelligence,IEEETransactionson,2013,35(8):1972-1984.

[8]BäkS,CorveeE,BremondF,etal.Boostedhumanre-identificationusingriemannianmanifolds[J].ImageandVisionComputing,2012,30(6):443-452.

[9]YuiManLui.AdvancesinMatrixManifoldsforComputerVision[J].ImageandVisionComputing,2012,30(7):380-388.

[10]SommerS,LauzeF,NielsenM.OptimizationoverGeodesicsforExactPrincipalGeodesicAnalysis[J].AdvancesinComputationalMathematics,2013,38(2):281-320.

[11]PennecX,FillardP,AyacheN.ARiemannianframeworkfortensorcomputing[J].InternationalJournalofComputerVision,2006,66(1):41-66.

[12]CaseiroR,MartinsP,HenriquesJF,etal.AnonparametricRiemannianframeworkontensorfieldwithapplicationtoforegroundsegmentation[J].PatternRecognition,2012,45(11):3997-4017.

[13]HALLSB,LIEG.Liealgebras,andRepresentations:anElementaryIntroduction[M].NewYork:Springer,2003.

[14]SaitohS.Theoryofreproducingkernelsanditsapplications[M].Harlow,England:LongmanScientific&Technical,1988.

(责任编辑杨继森)