基于蒙特卡洛方法的大型动态水面建模与仿真技术
2015-12-23杨振军,杨雨迎,范栋等
【基础理论与应用研究】
基于蒙特卡洛方法的大型动态水面建模与仿真技术
杨振军a,杨雨迎a,范栋b,高玉琳b
(装甲兵工程学院a.兵器工程系; b.训练部,北京100072)
摘要:针对激光探测中大型动态水体表面的波浪干扰问题,研究了基于PM功率谱的水面波浪线性模型, 利用蒙特卡洛方法对波浪模型进行了仿真;通过对不同风速和风向的二维粗糙水面仿真结果的分析,提出的粗糙水面模型以及蒙特卡洛仿真方法满足实际需求,且仿真效果与实际情况相符。
关键词:动态粗糙水面;功率谱函数;蒙特卡洛;仿真
收稿日期:2014-11-15
作者简介:杨振军(1973—),男,讲师,主要从事武器系统发射理论与技术研究。
doi:10.11809/scbgxb2015.06.032
中图分类号:TP391
文章编号:1006-0707(2015)06-0128-03
本文引用格式:杨振军,杨雨迎,范栋,等.基于蒙特卡洛方法的大型动态水面建模与仿真技术[J].四川兵工学报,2015(6):128-130.
Citation format:YANG Zhen-jun, YANG Yu-ying, FAN Dong,et al.Research on Dynamic Sea Surface Modeling and Simulation Technology Based on Monte Carlo Method[J].Journal of Sichuan Ordnance,2015(6):128-130.
Research on Dynamic Sea Surface Modeling and Simulation Technology
Based on Monte Carlo Method
YANG Zhen-juna, YANG Yu-yinga, FAN Dongb, GAO Yu-linb
(a.Department of Arms Engineering; b.Training Department,
Academy Armored Forces Engineering, Beijing 100072, China)
Abstract:Aiming at wave disturbance problem of laser detection on huge dynamic sea surface, this paper studied the linear model of waves based on PM power spectrum, and simulated the linear model using Monte Carlo method. Through the analysis of simulation results of two-dimensional rough sea surface under different wind speed and direction, the rough surface model and the Monte Carlo simulation method presented in this paper meet actual demand, and the simulation results act in accord with actual situation.
Key words: dynamic rough surface; power spectral function; Monte Carlo; simulation
利用激光探测大型水体水面或者水上目标时,例如海洋和湖泊,其表面波浪的波动是影响激光测距精度的重要干扰因素。为有效区分目标和波浪,需要对自然界大型水体表面进行建模和仿真。
国内外对大型动态水面模型研究较多,文献[1]采用数值迭代方法求解二维的 Navier Stokes 方程,该方法生成的海浪形状比较真实,但实时性方面稍显不足;文献[2]采用双叠加法模型,对三维不规则短峰波海浪进行了仿真,得到了较为真实理想的海浪模拟效果;文献[3]比较、验证了线性叠加法和线性滤波法,讨论了谱窗估计和最大熵谱估计方法;文献[4]基于海面功率谱,建立了海面的Weierstrass分形函数模型。目前,研究较为成熟的海浪数值模拟方法大多是基于线性海浪理论,本文主要基于线性海浪理论,对大型动态水体表面模型进行研究,并利用蒙特卡洛方法对模型进行仿真。
1动态水面的数学描述
线性叠加法认为大型动态水体表面波浪是由许多不同波动特性的组成波叠加而成。大型水体表面是在大尺度、近似周期性的波浪上叠加了波纹(小尺度波浪)、泡沫和浪花等。由于风作用于水面,与水面产生摩擦使水体产生波动,从而产生了波;风的持续作用形成波浪,继而形成涌,涌由一些具有长波长、类似正弦波的波浪组成[5]。通常将波浪看作无限个不同波高、不同频率、不同相位、不同传播方向的随机余弦波叠加而成:波浪主要由短波组成,大量的短波之间的非线性作用将能量传递给较长波长的波,直至能量损耗和波的个数增加达到平衡态;风速越大,这些汇聚能量的中长波的波长越长;长波在时间和空间上均具有良好的持续性;水面任一点的波都是本地短波和远处传来中长波的叠加。
基于上述分析,可将波浪的数学模型表述为[6]
cos(kmxcosθn+kmysinθn-ωmt+φmn)
(1)
其中f(x,y,t)为t时刻水面任意一点(x,y)的波动的瞬时高度;Δω是频率离散间隔,采用频率等分法或能量等分法;Δθ为方向离散间隔,根据离散点数分割仿真长度计算;km为各分量波的波数;φmn为服从均匀分布[0,2π]的随机初相位值;ωm为波频;W(ω,θ)为方向功率谱函数
W(ωm,θn)=W(ωm)G(ωm,θn)
(2)
其中:W(ω)为功率谱函数;G(ω,θ)称为方向函数,本文采用波浪立体观测计划(SWOP)的公式[7]
(3)
(4)

(5)
其中ω0为频率取ωm时的谱峰频率。
动态粗糙水面的功率谱密度函数W(ω)定义为水面起伏高度相关函数的傅里叶变换,表征了构成粗糙水面的各谐波分量相对于空间频率ω和方位角θ的分布。针对海浪功率谱,本文采用PM谱。PM谱的表达式为[8]
(6)
其中,α、β为无量纲常数,α=8.1×10-3,β=0.74;g为重力加速度,g=9.81 m/s2;U19.5为水面19.5 m高度处的风速。
2动态粗糙水面的蒙特卡洛仿真
2.1仿真算法
基于蒙特卡洛方法的动态粗糙水面仿真程序流程如图1所示。
频率和方位角区间离散化时,按频率等分法分割成M份,离散间隔为Δω,Δω=(ωM- ω1)/M;离散点值取区间频率均值(ωi+ ωi+1)/2,其对应的频率谱W((ωi+ ωi+1)/2)。方位角θ的等分成N份,每段间隔为Δθ,Δθ = (θN- θ1)/N。其次,ω0为频率取ωm时的谱峰频率,可将功率谱W(ω)对频率ω求偏导,令偏导为零求得ω0=8.596/U19.5。

图1 动态粗糙水面仿真程序流程
2.2蒙特卡洛仿真实现
基于PM谱,利用蒙特卡洛方法,在t=0时刻,对不同风速和风向的二维粗糙水面进行了仿真,如图2所示。
3结论
根据图2中不同风速和风向的二维粗糙水面仿真结果,可以得出:
1) 当风速较小时,海面的局部小尺度波纹变化很快,但整体水面的大尺度波浪的起伏较小;当风速增大时,水面的整体起伏较大,但局部变化变慢,这与一般大型水体水面的自然变化规律相符。
2) 当风向不同时,波浪起伏和运动的方向不同。无论是风速较大时整体的大尺度波浪还是风速较小时局部的小尺度波纹,起伏和运动的方向均随风向的变化而变化;当风速分别取互相垂直的角度时,水面波浪起伏和运动的方向也互相垂直。
因此,基于PM谱的粗糙水面的蒙特卡洛仿真方法适用于大型水体表面的建模要求,且仿真效果与实际情况相符。
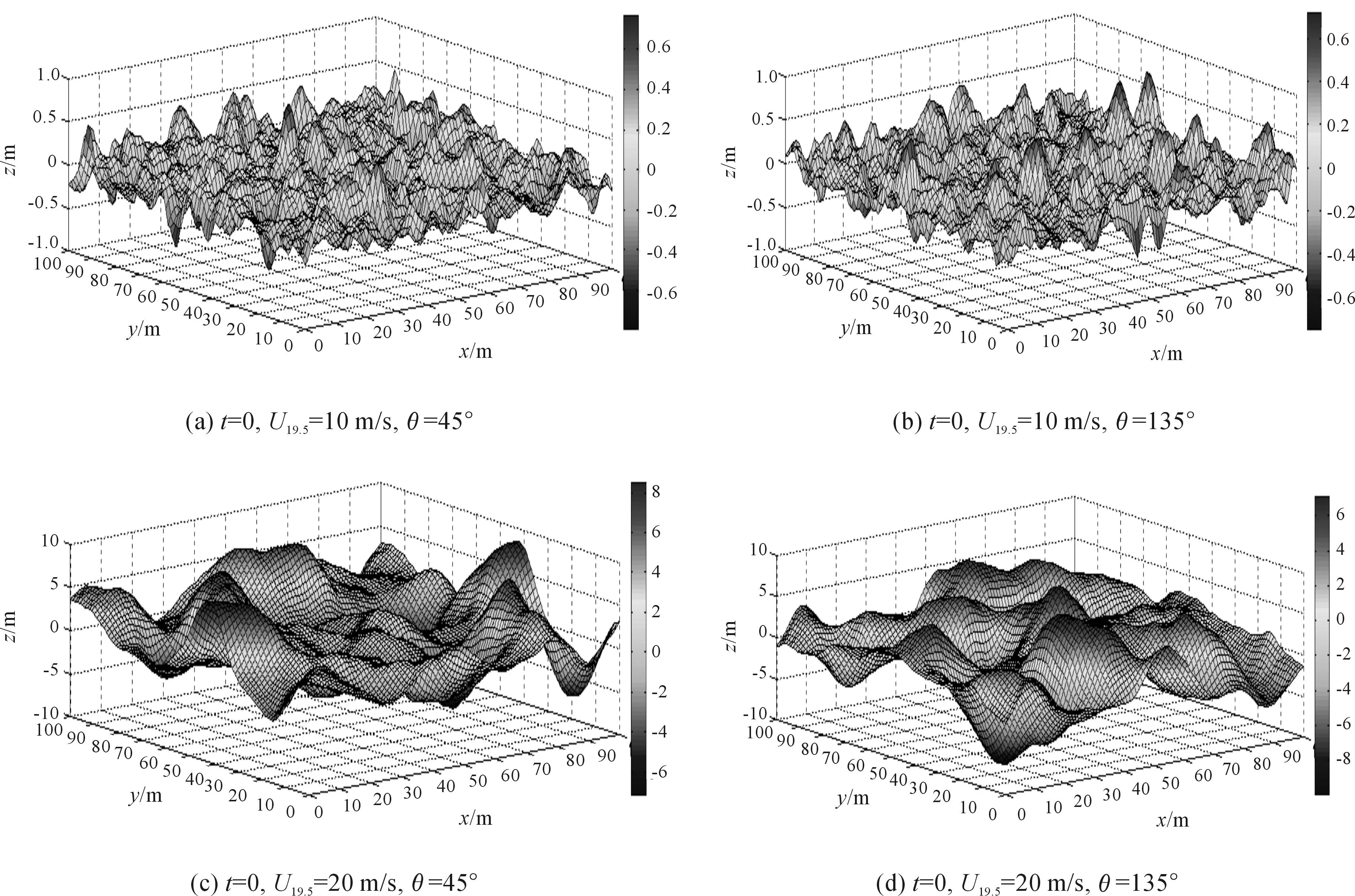
图2 不同风速和风向的选取对二维粗糙水面仿
参考文献:
[1]FosterN,MetaxasD.Modelingwaterforcomputeranimation[J].CommunicationsoftheACM,2000,43(7):60-67.
[2]李晖,郭晨,李晓方.基于Matlab的不规则海浪三维仿真[J].系统仿真学报,2003,15(7):1057-1059.
[3]杨惠珍,康风举,楮彦军.基于海浪谱的随机海浪仿真及验证[J].系统仿真学报,2005,17(10):2324-2326.
[4]姚纪欢,方艺东,肖景明,等.动态海面的分形模拟及其电磁散射[J].西安电子科技大学学报,1999,26(6):763-766.
[5]郭立新,王蕊,吴振森.随机粗糙面散射的基本理论与方法[M].北京:科学出版社,2010:105-107.
[6]徐德伦,于定勇.随机海浪理论[M].北京:高等教育出版社,2001:87-89.
[7]罗玉.3D海浪动画模拟技术研究[D].武汉:武汉理工大学,2008.
[8]钟珊珊.冲击线性信号的神经网络仿真[J].重庆工商大学学报:自然科学版,2014,31(1):69-73.
[9]EricIThorsos.AcousticscatteringfromaPierson-Moskowitzseasurface[J].JournaloftheAcousticalSocietyofAmerica,1990,88(1):335-349.
(责任编辑蒲东)
