电动绳系在低极轨卫星中的应用研究

全荣辉，许 猛，程世豪

（南京航空航天大学 航天学院，南京 210016）

0 引言

轨道高度1000 km 以下的低极轨（low altitude polar orbit）卫星具有轨道周期短、对地观测分辨率高等优点，在遥感等领域具有广阔的应用前景，国外已有DMSP、SPOT 等卫星系列[1-2]。但低极轨卫星的大气阻力效应十分明显，严重地限制了卫星的轨道寿命。随着未来航天技术的发展，对低极轨卫星的使用寿命要求进一步提高。若采用常规燃料推进方式维持卫星轨道高度，则 长寿命（例如10年）低极轨卫星所需燃料的重量将远超过卫星主体与载荷重量。

为提高低极轨卫星的使用寿命，科研人员一直在致力于其他推进方式的研究，其中包括电动绳系驱动方式。电动绳系采用通电导体切割地球磁力线所产生的洛仑兹力为卫星提供推力，用于卫星轨道的机动操作[3]。根据电动绳系电流方向与地球磁场方向的相对关系，可以由左手定律得到洛仑兹力方向。电动绳系所需的电极偏压与驱 动电能可以由太阳电池板提供。电动绳系包括水平结构和竖直结构两种，其中竖直结构在重力作用下，相比水平结构更容易展开和保持平衡，但同样面临严重的动力学振荡问题[4-6]。竖直结构电动绳系适用于赤道和低纬度地区卫星推进；而在高纬度地区，由于竖直结构绳系电流方向与地球磁场方向接近平行，无法产生足够的洛仑兹力实现推进，所以水平结构电动绳系适用极轨卫星的轨道机动。在进行电动绳系结构设计时，既要考虑推力和大气阻力的大小，还要考虑绳系的强度[7]。

本文提出了水平结构电动绳系方案并进行了分析计算，采用国际参考地磁模型（IGRF11）和电离层模型（IRI07）计算得到了低极轨卫星在轨道不同位置的电动绳系推进力，同时结合国际参考大气模型（NRL-MESIS00）计算了卫星受到的大气阻力；对绳系的推力和大气阻力进行比较分析，确定电动绳系的适用轨道区域及适合的卫星尺寸。

1 水平结构电动绳系

电动绳系的研究始于20世纪70年代[8]，国外已进行了多次电动绳系的卫星飞行试验，初步验证了电动绳系用于推进/反推进的可行性[9-12]。虽然电动绳系与卫星同处于失重状态中，但由于系绳较长，在运动中容易振荡，系绳越长则由两端受力不平衡而造成的振荡现象越明显[13]。

本文提出的水平结构电动绳系方案如图1所示，由2 颗卫星构成，2 颗卫星之间采用半刚性的导体系绳连接，处于同一水平面。其中1 颗卫星通过偏压导体收集空间电子，另1 颗卫星通过空心阴极向空间发射电子，此时在导体系绳上产生电流回路。在地球磁场垂直分量Bz作用下，水平系绳可以产生与卫星运动方向相同的推力分量，进而实现对卫星轨道的提升；当系绳上电流方向相反时，所产生的洛仑兹力方向也相反，此时电动绳系对卫星产生阻力，可以用于卫星轨道降低。地球磁场随纬度的分布如图2所示，磁场垂直分量Bz在南北半球方向相反，大部分区域磁场强度均达到104nT 以上。电动绳系的有效作用区域应选取Bz分量达到104nT 的区域，否则磁场强度过小会导致电动绳系推力不足。以北半球为例，在北纬20°以上，地球磁场的Bz分量大于104nT，方向垂直向下。若采用北半球作为推进控制区域，当低极轨卫星到达北纬20°以上时，即可以开启电动绳系系统，逐步提升卫星轨道高度；当低极轨卫星向南运动离开北纬20°以上区域时，即关闭电动绳系系统，对系绳进行自然冷却。电动绳系的开启与关闭可以结合磁场分量探测自动进行，无须地面不间断跟踪操作。

图1 水平结构电动绳系示意图 Fig.1 Schematic diagram of the horizontal electrodynamic tether system

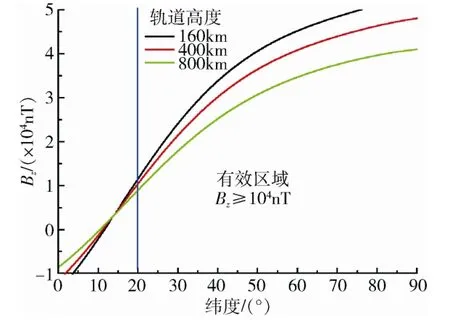
图2 地球磁场垂直分量随纬度分布（北半球，东经 120°） Fig.2 The Earth magnetic field Bz component as a function of latitude (North hemisphere,longitude 120° east)

本方案中，电动绳系对卫星推进时间仅覆盖部分轨道，小于大气阻力作用时间（全轨道），因此电动绳系产生推力的冲量要与大气阻力的冲量相当，才可以达到维持轨道高度的目的。相比竖直结构绳系，水平结构绳系无法利用万有引力差来实现自然展开，因此需要依靠卫星小推力和精确的姿态控制来实现。水平结构绳系与竖直结构绳系均存在由角度偏差或系绳弯曲造成的有效长度问题。对于水平结构绳系来说，系绳两端卫星应尽量保持在同一高度和同一纬度线上。水平结构绳系除了面临振荡问题，还遇到因系绳的温度变化所带来的系绳安全和工作效率问题。由于篇幅限制，本文主要探讨水平结构绳系在低极轨卫星中的应用潜力。

2 数值计算及分析

选取160/400/800 km 高度、90°倾角的轨道作为典型轨道进行分析。其中160 km 为LEO 轨道 的高度下限，400 km 为国际空间站轨道，800 km为太阳同步卫星轨道。电动绳系工作期间需要从空间等离子体中收集和释放电子形成电流回路，因此其推进效率除受到地球磁场环境影响外，还与空间电子密度和电子温度相关[14]。本文采用国际地磁参考模型（IGRF11）、国际参考电离层模型（IRI07）和标准大气密度模型（NRLMSIS00）计算了上述3 个轨道，一个轨道周期（起始点北纬0°，东经120°）内卫星所经历的地球磁场Bz分量、电子密度、电子温度和大气密度变化，如图3所示。

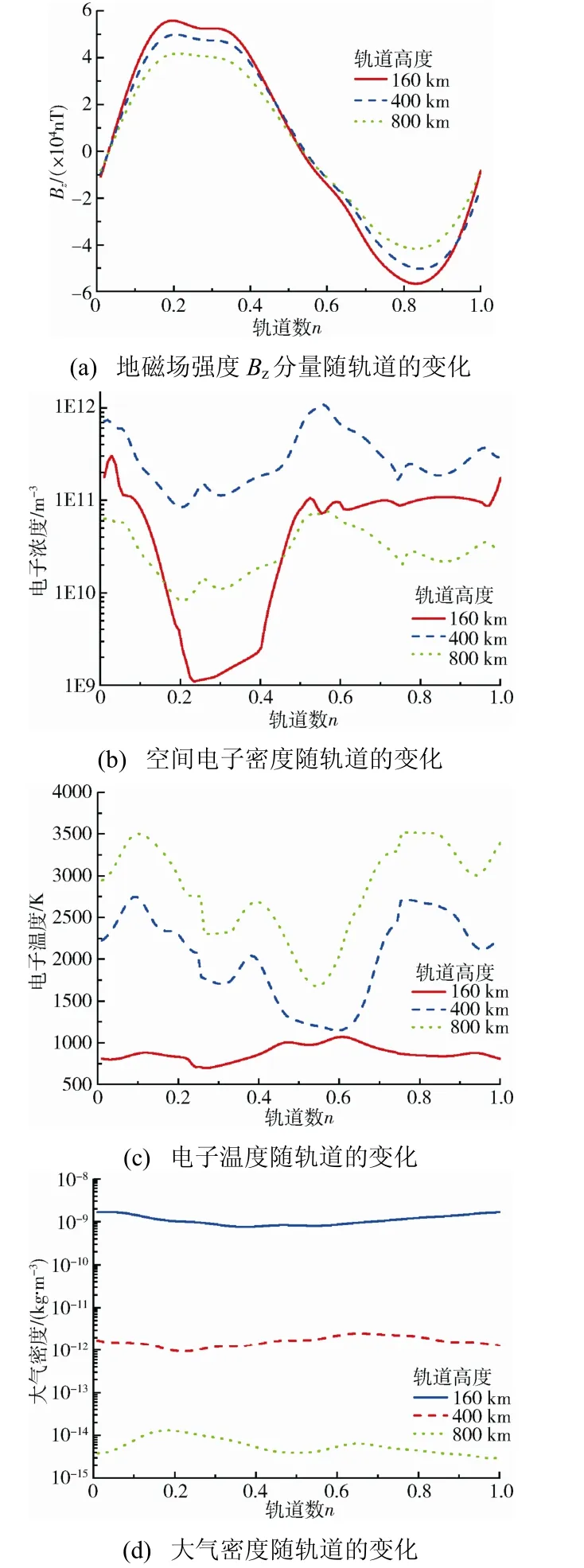
图3 低极轨卫星所经历的空间环境变化 Fig.3 Space environment encountered by low attitude polar orbit satellites during one cycle

图3中的计算结果基于地磁活动平静期。在空间天气剧烈活动情况下，电子密度可增大1～2个量级，大气密度也可增大1 个量级左右，计算结果可能会偏小。不过与卫星轨道寿命相比，这种扰动持续时间较短，不影响电动绳系对低极轨卫星的总体推进效果。由图3可见，地球磁场Bz分量、电子密度和电子温度均随着卫星所在具体轨道位置变化而剧烈变化。其中地球磁场Bz分量随着轨道高度增加而减小，但减小幅度不大；空间电子密度在400 km 左右达到最大值，而160 km和800 km 相对较小；电子温度随着轨道高度增加而增加；大气密度随着轨道高度增加呈指数下降，但随轨道位置变化不大。因此根据上述空间环境特征，可知相同轨道高度的电动绳系电流将随着轨道位置改变而变化，而卫星所受到的大气阻力则相对稳定。

电动绳系电流除与空间电子密度相关外，还取决于电子收集方式。在水平结构电动绳系中，如采用裸露的系绳导体收集电子，将导致系绳上电流分布不均匀而产生力矩，引起卫星系绳方向与卫星运动方向夹角减小，最终使卫星偏离原轨道并不断旋转。因此该方式并不适用本文水平结构绳系。水平结构电动绳系可以采用传统的球形导体在一端收集电子，其收集的电子电流符合Parker-Murphy 定律，具体表述为[14]

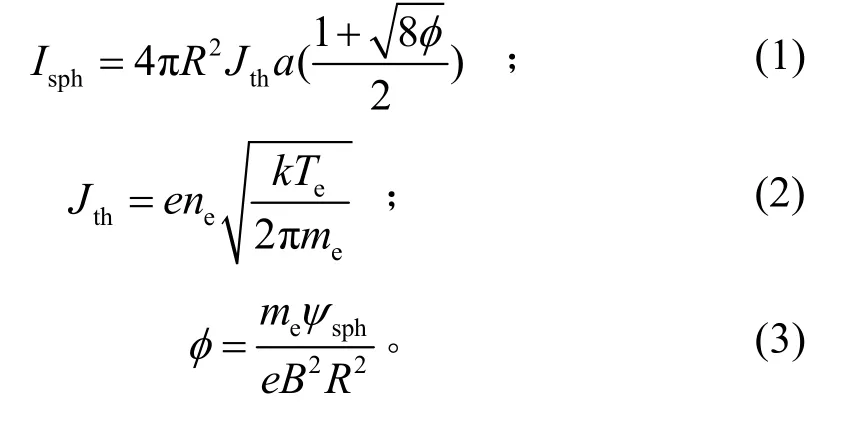
式中：Ⅰsph为收集的电子电流密度；R为球形导体的半径；Jth为热电子电流；a为拟合常数，根据TSS-1R 绳系卫星实验结果，取a=2.16；e为电子电量；ne为电子密度；Te为电子温度；k为玻耳兹曼常数；me为电子质量；ψsph为球形导体偏压；B为总的磁感应强度。

图4给出了不同轨道高度的球形导体所收集的系绳电流随偏压与轨道高度的变化。由图4(a)可见系绳电流随着偏压升高而增加，但在100 V 以上增加幅度逐步减缓，因此本文的计算中采用的偏压大小为100 V；图4(b)表明系绳电流在400 km时达到最大值约0.1 A，这与图3(b)中空间电子密度变化密切相关。当系绳电流增加时，电子发射端喷射电子时将受到反推力作用：以电流0.1 A、温度1000 K 的电子喷射为例，对喷射极的作用力约为10-8N。这个作用力对于大尺寸卫星可以忽略，但对微卫星和纳卫星却是不可忽略的因素。

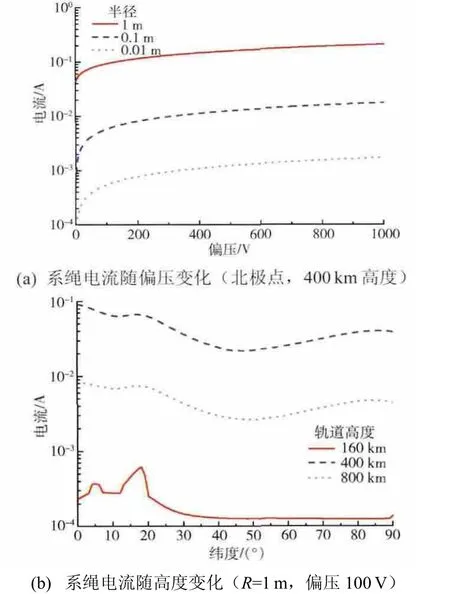
图4 系绳电流随偏压与轨道变化 Fig.4 The tether collective current as a function of bias voltage and orbit altitude

在确定系绳电流Ⅰsph后，由洛仑兹力公式可 以得到电动绳系产生的推力为

因此根据不同轨道位置的空间环境参数，结合系绳有效长度等参数，最终可以得到电动绳系产生的洛仑兹力随轨道的变化。卫星在轨所面临的大气阻力为[15]

式中：ρ为大气密度；Cd为阻力系数；A为卫星横截面积；v为卫星速度。引入球状系数β=CdA/M，式(5)也可以表述为阻力加速度，即[16]

在本文计算中，采用如表1所示卫星参数，其中β取0.04。

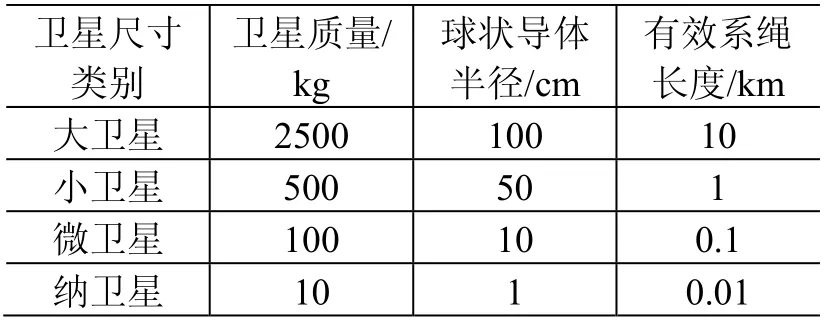
表1 计算中所采用的卫星参数 Table1 The satellite’s parameters used in calculation

采用式(4)～式(6)结合式(1)与空间环境参数特征，可以得到不同轨道高度各种尺寸卫星的洛仑兹推进力与大气阻力的对比结果，如图5所示。

由图5可见，在160 km 轨道上，不同尺寸卫星的大气阻力远大于系绳推力，因此该轨道并不适合采用电动系绳推进抵偿大气阻力；400 km 轨道上，大卫星的系绳推力大于大气阻力约1 个量 级，小卫星的则量级相当，而微卫星和纳卫星的均小于大气阻力1～2 个量级，因此该轨道高度大卫星适合采用电动绳系来抵偿大气阻力，小卫星可以采用电动绳系减缓大气阻力的影响，但无法完全抵销大气阻力；在800 km 轨道上，大卫星的系绳推力大于大气阻力约2 个量级，小卫星的大1个量级，微卫星的大2 倍以上，而纳卫星的小于1个量级，因此该轨道上大卫星、小卫星和微卫星均适合采用电动绳系推进抵偿大气阻力。

图5中推进区与反推进区是相对的，在不调整卫星姿态的情况下，可以根据测控或推进要求选择北半球或南半球作为推进区域。需注意的是，在图5(c)中，小卫星的系绳推力仍大于大卫星的大气阻力，因此大卫星的系绳长度缩减到 1 km 也可以满足推进要求，进而减小了系绳展开与控制的技术难度，同时为系绳附加在其他卫星机构上或使用刚性连接杆提供了一种可能。

3 结束语

本文提出了采用水平结构电动绳系产生洛仑兹力抵偿大气阻力的方法，分析了低极轨卫星在160、400 和800 km 高度所经历的地球磁场、空间电子和大气环境，对比了不同尺寸低极轨卫星的系绳推力和大气阻力大小。分析结果表明，水 平结构电动绳系适合于大尺寸卫星在高度400 km以上轨道使用，其产生的电动绳系推力足以抵偿大气阻力的影响。在800 km 轨道，系绳长度可以缩短至1 km，在小卫星和微卫星上该方法也具备应用前景。文中的分析仅限于对系绳推进力与大气阻力关系的探讨，未涉及电动绳系的具体技术问题。在实际工程应用中，水平结构电动绳系所带来的飞行控制、绳系的展开与平衡以及空间环境的扰动等问题均是不可忽略的因素，这在后续的工作中需进一步分析与试验。

（References）

[1] Vaivads A,Ander M,Buchert S,et al.What high altitude observatons tell us about the auroral acceleration: a cluster/DMSP conjunction[J].Geophys Res Lett,2003,30(3): 1106

[2] Satellite and sensors - SPOT[R/OL].[2015-05-01].http://eoedu.belspo.be/en/satellites/spot.htm

[3] Neter E,Kane T R.Electrodynamic forces in tethered satellite systems part I: system control[J].IEEE Trans on Aerospace and Electronic Systems,1994,30(4): 1031

[4] Anselmo L,Pardini C.The survivability of space tether systems in orbit around the earth[J].Acta Astronautica,2005,56: 391

[5] Zhong R,Zhu Z H.Long term dynamics and optimal control of nano-satellite deorbit using a short electrodynamic tether[J].Advances in Space Research,2013,52(8): 1530

[6] Iñarrea M,Lanchares V,Pascual A I,et al.Attitude stabilization of electrodynamic tethers in elliptic orbits by time-delay feedback control[J].Acta Astronautica,2014,96(1): 280

[7] Khan S B,Sanmartin J R.Analysis of tape tether survival in LEO against orbital debris[J].Advances in Space Research,2014,53(9): 1370

[8] Banks P M.Review of electrodynamic tethers for space plasma science[J].J Spacecraft and Rockets,1989,26(4): 234

[9] Stone N H,Bonifazi C.The TSS-1R mission: overview and scientific context[J].Geophys Res Letters,1998,25(4): 409

[10] Kashihara K,Cho M,Kawamoto S.Ground experiments and computer simulations of interaction between bare tether and plasma[J].IEEE Trans on Plasma Science,2008,36(5): 2324

[11] 孔宪仁,徐大富.空间绳系研究综述[J].航天器环境工程,2010,27(6): 775 Kong Xianren,Xu Dafu.The studies of space tether[J].Spacecraft Environment Engineering,2010,27(6): 775

[12] Iki K,Kawamoto S,Morino Y.Experiments and numerical simulations of an electrodynamic tether deployment from a spool-type reel using thrusters[J].Acta Astronautica,2014,94(1): 318

[13] 李然,许滨,张珩.空间电动绳系推进中导电系绳动态特性分析[J].振动与冲击,2008,27(6): 36 Li Ran,Xu Bin,Zhang Heng.Dynamic feature analysis of space electrodynamic tether systems[J].Journal of Vibration and Shock,2008,27(6): 36

[14] Chaganti V S R K R,Singh N.Current collection by a conducting spherical satellite in ionosphere[C]// Southeastcon '92 Proceedings,IEEE,1992-01: 75

[15] Prieto D M,Graziano B P,Roberts P C E.Spacecraft drag modelling[J].Progress in Aerosp Sci,2014,64: 56

[16] Storz M F,Bowman B R,Branson M J I,et al.High accuracy satellite drag model(HASDM)[J].Adv in Space Sci,2005,36: 2497