房产价格与固定资产投资效率的空间集聚关系研究

常宝瑞

一、研究背景

伴随着当前经济的下行态势，一直过热的房地产市场也终于转冷，使其长期积累的问题与矛盾逐步突显。从时间角度划分，自1998年房改以来，被长期抑制的住房需求被释放（居民改善性住房需求），截止到2002年，此期间土地供应充沛，房产价格相对稳定。2003至2007年中国经济增长步入快车道，房地产业扩张及房产价格上涨迅猛，土地价格攀升，投资性需求旺盛。2008年至今，从金融救市到抑制房价过高过快增长，再到现如今房产泡沫破裂的悲观市场预期，房地产业几经沉浮。在高涨的房价背后，更多的是多方利益的博弈（政府、金融行业、开发商、一般性消费者、投机性群体等）。

房地产业具有关联度高、拉动性强的特点，是推动经济增长的支柱产业之一。国内对于房产价格的空间联系研究较少，即在探讨当前房产价格形成过程中，一方面缺失了重要的地理关联性信息，另一方面，也造成了模型设定的误差，降低现实模拟度。潘文卿（2012）运用探索性空间数据分析研究了中国1988年～2009年间各省人均GDP空间分布格局，结果表明存在正向空间自相关性，并且显著性随时间推移而增大，集聚性特征突出，其实证研究表明空间溢出效应是中国区域经济发展不可忽视的重要影响因素。王鹤（2012）分析发现房地产价格具有空间自相关性，其利用空间滞后模型分析1999年～2009年省际面板数据，结果表明东部地区房价主要由空间因素决定，西部地区房价受供给与需求因素主导，而中部地区房价受两者共同影响。相关文献表明，房产价格存在显著空间关联性（空间集聚），且具有空间溢出效应。

本文以地级市为基础空间分析单元，通过房产价格、地方固定资产投资效率及其空间关联性研究，试探寻房产泡沫破裂可能发生的空间轨迹。引入空间误差模型，以及具有局部空间自相关特征的地理加权回归模型进行对比研究。

二、数据来源及变量选取

数据来源于《中国区域经济统计年鉴2012》、《中国城市统计年鉴2012》，以及31个省份2012年地方统计年鉴。地理底图源自国家基础地理信息系统县级以上居民地，依据中华人民共和国最新地级行政市划分设置状况（如2003年广西成立崇左市，2004年宁夏成立中卫市），运用ArcGIS map软件对县级矢量单位进行绘制合并，共计358个单元（包含直辖市、副省级城市、地级市、区、州、盟等）。其中重庆直辖市因同级别中行政面积最大，故依据重庆市地方统计年鉴，由2007年起将其划分为重庆一小时经济圈、渝东北翼、渝东南翼三大区域，而海南省除海口市、三亚市以外，其余地区均计作海南省直辖县。地级市作为次区域中心，能较好地反映辖区内经济发展水平与房产价格关系，并且数据较为完备。在时间选取上，2011年恰逢中国房地产价格高点，且具有全国普遍性特点，此时房产价格的区位关系显示度更为明显。

土地面积（Land Area，单位：平方公里），年底总人口数（Total Population，Totalpop，单位：万人），地区平均人口密度（Density of population，Densitypop，单位：人∕平方公里），因各省人口统计口径不一致，部分省份无地级市常住人口数据，故采用年底总人口数。地区生产总值（Gross Regional Product，GRP，单位：亿元），及各地级市一、二、三产业产值（AGR、IND、SRV，单位：亿元）与人均地区生产总值（PerGRP，单位：元∕人）。固定资产投资不含农户（Total Investment in fixed Assets，TFAssets，单位：亿元）。商品房销售额（To Sales，单位：亿元）与商品房销售面积（Space Sold，单位：万平方米），本年度房屋建筑施工面积（Floor space of buildings under construction，简记为Under，单位：万平方米）与房屋建筑竣工面积（Completed in construction，简记为Completed，单位：万平方米）。

三、固定资产投资效率与空间集聚性分析

数据包络分析(Data Envelopment Analysis，简称DEA)基于“相对效率”概念，以凸分析与线性规划为工具，比较决策单元（Decision Making Units，DMU）偏离前沿面（实为最优化条件曲线，视为可行域边界）的程度，以相对有效性判定最优方案。其假设输入输出值间存在某种必然关系，但不确定关系的具体表达式，适用于多种输入输出的综合有效性评价问题，对数据无需进行“无量纲化处理”，无需构建权重假设，依据客观数据求得最优权重，排除主观因素干扰。

在DEA模型设置上，选择规模可变模型VRS，拟合实际情况，即各地方政府以产出最大化为目标，唯GDP论寻求政绩最大化。结果发现（见表1）当投入不变，产出最大化情况下，各地均呈现出规模报酬递减趋势（drs），虽无投入冗余，但产出距最优前沿面上尚有差距，即投入使用效率低于最优比率。而在产出不变，投入最小化情况下，各地区均无产出冗余，但皆表现为投入冗余状况，全局呈规模报酬递增趋势（irs）。各地方政府在固定资产投入上，均存在投资效率低下或冗余式增长（重复建设）状况，其中又以房地产开发占比最高，而住宅开发又占了房地产开发55%以上的规模。对比发现，房产开发值占固定资产投资比例与地区经济增长状况成正向关系，如以北、上、广、深为代表的一线城市及区域中心城市占比高达40%～55%，而经济发展较弱的省份反而占比较低，为25%～35%之间。

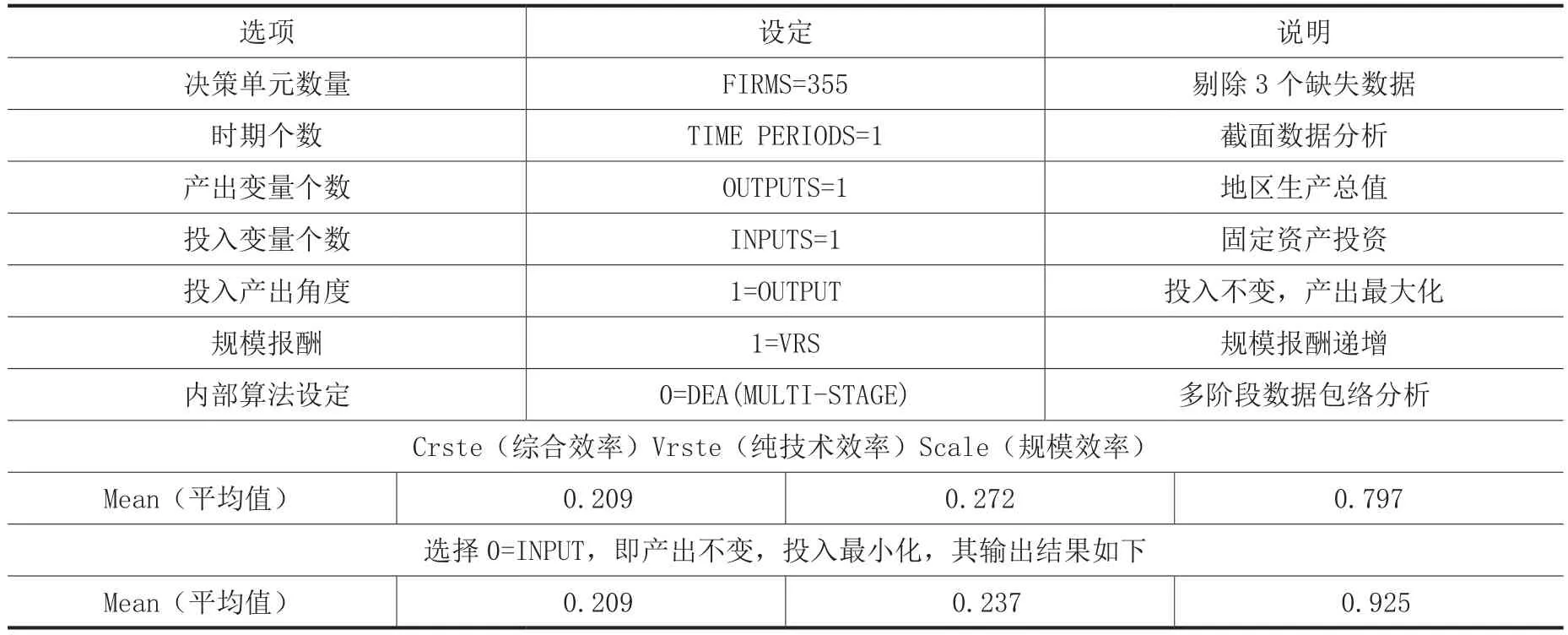
表1 DEA设定及输出结果表

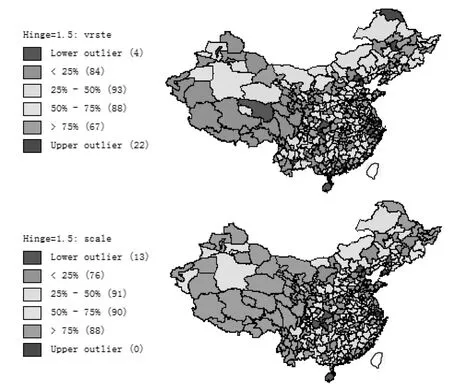
图1 固定资产投资效率空间分位图

将DEA生成的固定资产投资效率比导入数据底图，借由探索性空间数据分析（Exploratory Spatial Data Analysis，ESDA）进行研究。图1分别为纯技术效率（vrste）与规模效率（scale）的1.5倍箱图，全距hinge=1.5倍，一倍的大小为四分之一与四分之三位数间的距离，大于或小于全距，为极端值outlier。

如图1所示，以技术规模效率为主的地区主要集中于东部地区及部分中部地区与少数西部地区，且具有较强的省际界线，围绕着22个主要集聚效率地带外延出次级梯队。而规模效率集聚主要分布于西部地区，以及部分中部、东北部与少数东部地区。规模效率群的城市梯队等级性较弱，而技术效率群的城市等级分化明显。归纳总结，综合性规模效率具有地域性差异与城市层级性差异特点。

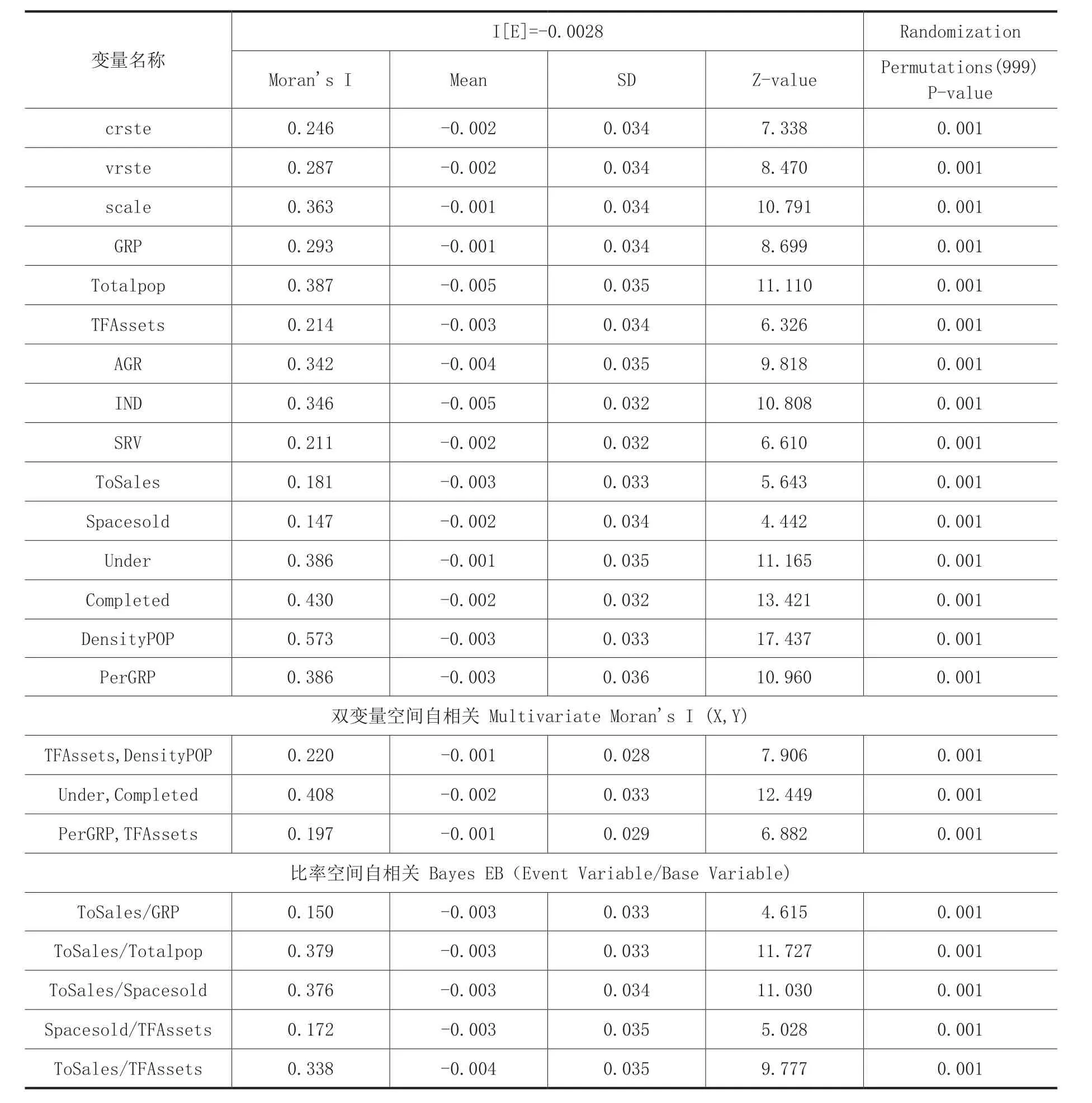
表2 全局空间自相关输出结果表

空间矩阵的建立，一般分为两种方法，分别基于相邻性关系或基于距离因素，以相邻性基础构建又可分为Rook相邻（车相邻，上下左右四个方向的点或边相邻）与Queen相邻（后相邻，上下左右加对角线共八个方向的点或边相邻）两种确立方法。因各地理单元相邻性较好，分析范围全境基本无飞地或离地，且各单元行政边界多为不规则多边形，相邻性关系复杂，故选用Queen相邻构建空间权重矩阵。

Moran's I统计是检验全局聚类的方法，显示选中区域内各单元间是邻近相似还是相异，或是相互独立的关系，即表示空间正相关、负相关或不相关关系。Moran’s I的取值位于-1到1之间，取值在0以上表示正相关，当值接近于1时，表明具有相似属性的区域聚集在一起，即高-高相邻或低-低相邻。当小于0时，表示为负相关，值接近于-1时则表明具有相异属性值的区域集聚在一起，即高-低值相邻或是低-高值相邻。如Moran’s I接近于0时，则表示研究区域的特征属性是随机分布的，不存在空间自相关性。

理论平均值E[I]，经验分布的平均值Mean，标准差SD，Z检验值, 参考分布的序列数量（Permutations），假设显著性水平（P-value）。

Z值的判别应用跟I值类似，当Z为正号，且通过显著性检验，如大于1.96，表示有正相关，存在高值集聚区（HH）和低值集聚区（LL）两种情况。Z分数为负号，且通过显著性检验，如小于-1.96，表示负相关，有被高值包围区（LH）和被低值包围区（HL）两种情况存在。

蒙特卡洛检验（Randomization）用作检验Moran’s I的显著性分析，基于随机序列，多次重新计算产生一个参考分布，统计量与参考分布相比较，得出一个假设显著性。显著值P-value直接取决于序列数目，对99的序列，P=0.01，对999序列，P=0.001，本文采用999的序列数目进行参考分布模拟。

通过数据分析发现（见表2），各个变量均存在空间集聚趋势，且皆通过蒙特卡洛检验。从双变量空间自相关结果可以判断，固定资产投资与地区人口密度、房屋建筑施工面积与竣工面积，以及人均地区生产总值与固定资产投资在空间集聚上存在显著关联性，即利用所有相邻位置的平均值评估某一位置上的变量与其他变量的相关程度。施工与竣工面积集聚相关程度最高，作为衡量房产开发预期的重要指标。比率空间自相关，是运用经验Bayes(EB)调整，避免Moran散点图中比率方差不稳定的问题，其实质是一种直接变量标准化的方法。由表2可见，商品房销售额与地区生产总值、地区总人口数、商品房销售面积、地区固定资产投资，以及房屋销售面积与地区固定资产投资成比例空间集聚关系，即各变量间存在相关关系，且同时具有集聚趋势。

四、实证分析

本文采取横截面数据回归分析，即不同空间对象在同一时间点内所构成一维横截面数据集合，研究某时点上的某种经济现象，突出其空间差异性。横截面数据的特点就是离散性高，突出个体特性，表现个体差异。根据上文分析，剔除个别具有自相关性的变量，构建回归方程如下式（1）：

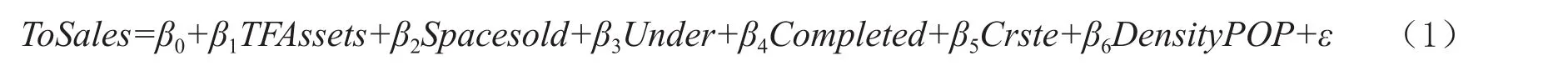
此章普通最小二乘法回归（OLS）仅作为对比参考，不进行详细解释说明。

（一）空间滞后模型

空间滞后模型（Spatial Lag Model，SLM），是将因变量的“空间滞后值”作为自变量纳入回归中来，解释了为什么距离相近的空间单元间观测值相似，因受“溢出效应”影响所致。空间滞后模型表达式为：

y为因变量，x为n×k阵的外生解释变量，ρ为空间回归系数，该模型反映了观察样本间的空间依赖性，即相邻区域的观测值ωy对本区域观测值y的影响程度与方向，ω为n×n阶的空间权重矩阵，ωy为因变量的空间滞后值，ε为随机误差项向量。距离滞后结构的本质是溢出效应随距离的延长而衰减，距离因素包括市场距离（在价值链上的相对位置）、技术距离（企业和产业之间的技术距离），以及空间距离这三类形式。要素溢出不是瞬时完成的，而是具有一定的滞后期。

（二）空间误差模型

空间误差模型（Spatial Errors Model，SEM），其解释某些因素会共同影响彼此的空间相邻性关系，从而造成这些空间单元的值相似，即把空间相关性看作一种干扰，模型识别中的依赖关系来自于误差项（某些未知因素在距离上相关）。其数学表达式如式（3）：

上式中，因变量y是n×1的向量。X是n×k的数据矩阵，代表解释变量。W是空间权重矩阵，参数λ为空间相关误差，即衡量样本观测值中的空间依赖作用，β为自变量对因变量的影响系数。ε为正常回归假设中的误差项（空间上满足不相关条件），而ξ为包含空间因素的误差项。

上述两种模型均存在自变量内生性问题。空间滞后模型是将因变量的“空间滞后值”作为自变量进行回归，因存在双向影响，故造成内生性。而空间误差模型一样存在双向影响作用的问题，以及误差项的相关性问题（观测值间通过误差相关彼此影响，又通过空间权重矩阵传导到自身）。因此，空间计量模型一般不采用最小二乘法（OLS），而采用极大似然法进行处理。

（三）地理加权回归模型

地理加权回归模型（Geographically Weighted Regression，GWR），是一种以局部参数估计构建的表达空间变化关系的线性回归，其认可空间变化关系的存在，并提供了可度量的研究方法。以上的空间滞后模型与空间误差修正模型都是建立在全局空间自相关的基础上的，对于局部空间关系缺乏解释力。地理加权回归模型是以局部空间自相关权重作为W，更加贴近于现实空间状况。地理加权回归（GWR）扩展了传统的回归框架，允许局部而不是全局的参数估计。其模型如式（4）：

其中(ui，vi)是第i个样本点的空间坐标，βk(ui，vi)是连续函数βk(u，v)在i点的值。如果βk(u，v)在空间上保持不变，则地理加权回归模型将变为全局空间回归模型。依据接近位置i的观测数据比远离位置i的数据对βk(ui，vi)的估计具有更强影响力（地理学第一定理），利用加权最小二乘法估计参数，得到：

其中W是空间权重矩阵，常用的空间权重函数主要以高斯函数为主，如式（6）：

其中，b是带宽，dij是样本点i和j的距离。带宽单位取决于“核类型”，在ArcGIS中CV法确定最佳相邻点数，对应于ADAPTIVE核，是指定近邻数的函数。也可基于ArcGIS中AICc法确定最佳距离，其对应于FIXED核，属于固定距离，用来解决各局部回归分析的空间环境。在“自适应”性内核下，带宽距离将根据输入要素类中要素的空间密度发生变化。带宽将成为最近相邻点数的函数，这样每个局部估计都将基于相同数量的要素，其用于分析相邻点的数目，而不是特定距离。本文选用“固定（FIXED）”内核确定地理加权矩阵，其带宽值将使用与输入要素类相同的单位来反映距离（例如使用UTM坐标对输入要素类进行投影，报告的距离将以米为单位），其Bandwidth=6.723。回归结果见表3。

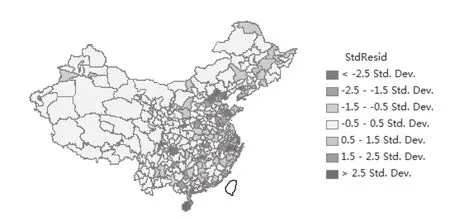
图2 GWR输出要素类残差图

表4 SLM与SEM模型的异方差性检验

本文运用LR似然比检验法与布鲁奇—培根检验法（Breusch-Pagan test）对模型异方差性进行检验，两者在性能上各有优劣，互为补充。检验结果表明（见表4），空间误差模型（SEM）的异方差性更小，拟合度更优。

从全局空间自相关拟合程度上分析（见表3），空间误差模型的拟合效果最优（0.899），即各单元间并不是直接影响而相互关联的，而是受共同第三方的影响。其映射的现实状况为中小城市的房产价格受其临近区域中心城市价格因素与城市发展预期等多因素的共同影响，形成空间上的相互关联集聚。其模拟性优于空间滞后模型因外部性所产生的溢出效用，即现实中房产价格的集聚状况不仅限于公共设置或公共服务等因素的空间外溢，还受到一些相关潜在因素的影响，本文将其视作城市化发展预期影响因素。

从局部空间自相关上分析，GWR拟合度优良，R2Adjusted=0.936。条件数：此诊断用于评估局部多重共线性。存在较强局部多重共线性会使得结果变得不稳定。本文输出结果为15.668＜30，与条件数相关联的结果为可靠，大于30为不可靠。映射Local R2值：该值范围在0.0与1.0之间，表示局部回归模型与观测所得y值的拟合程度。若此数值非常低，则表示局部模型性能不佳。本文Local R2值：0.0＜0.926＜1.0，表示其映射拟合度较好。Residual Squares：其为残差的平方和，此测量值越小，GWR模型越拟合观测数据，此值还在其他多个诊断测量值中使用。Effective Number：此值影响带宽的选择，是拟合值的方差与系数估计值偏差的折衷。当带宽趋近于无穷大时，观测值的地理权重接近于1，系数估计值接近于全局OLS 模型，其系数的有效数量接近于实际数量，局部系数估计值方差较小，但偏差很大。相反，当带宽趋近于0时，观测值的地理权重接近于零（回归点本身除外），系数的有效数量为观测值的数量，局部系数估计值方差较大，但偏差较低。Sigma：该值为正规化剩余平方和的平方根，即剩余平方和除以残差的有效自由度后的平方根，作为残差的估计标准差，故越小越好。Sigma适用于AICc计算。AICc：该值度量模型性能，主要用于比较不同的回归模型，但不作为拟合度的绝对度量，即具有较低 AICc值的模型将对观测数据拟合更好，适用于同一因变量且具有不同解释变量的模型。对比OLS与GWR的AICc值，是从全局回归到局部回归模型的优势比较。

如图2所示，其局部空间集聚性显著，且中心个数非唯一。一般以区域性中心城市为核心（可参考麦肯锡划分的中国22个城市消费群），呈现出由核心向外围逐层扩散分布，且东部集聚程度明显大于西部，城市密度更高，层级性特征更为显著。

五、结论

“新型城市化”演变畸形，成为一场政府、开发商、金融行业和普通消费者关于中国城市化的对赌造城运动；是对城市化预期的投注，周边外围区域追随核心区域城市扩张，价格水平受预期利好前景影响，逐步抬高；是一次对于集权体制的冲击，但并不会带来中心架构的崩塌，中心区反而是这场大洗牌的受益者，再次验证其区域政治中心、经济中心地位不可撼动（路径依赖），依旧是资本与人口集聚的最佳首选。而处于核心边缘区的三、四、五线城市将成为这场波及最大的受害者，他们将成为最早步入危机边缘的区域，同时也是最后走出寒冬的那一个。即房产价格的大面积下行波动并不会出现在北上广深等准一线城市，或者其他区域性中心城市，而是受资金链断裂和购买力下行压力影响最为明显的地级城市及县域城市（三、四、五线城市），它们才是这场中国式造城运动中最薄弱的一环（木桶理论），它们被视为经济大发展时期的主推手，是新型城市化的前沿地，但此时这些中小城市将经受一场前所未有的大考验。

土地财政与房屋价格限购前后政策的矛盾性。地方政府以土地出让鼓励房地产开发建设，以达到扩张城市面积、增加地方性财政收入与城建的双政绩效果，又以居民房产消费而增加地方税收，在整体上推动地方GDP增长，某种程度是因政府政策而推高了房产价格预期。而限购令的出台在某种程度上扼杀了房产的部分商品属性（消费属性、投资性、贮藏性等），以抑制投资解决房产价格过热，寄希望以商品房供应解决百姓住房问题（民生性问题，涉及保障房、安居房、廉租房建设问题），本身与市场规律相违背，具有冲突性，所以才会出现久治而无效的现象。

温州、杭州、长沙、鄂尔多斯等二、三线城市出现“以价换量”的房屋销售现象，实为地产商缓解资金压力，回笼资金（经济下行趋势预期影响）。而一些四、五线城市的中小开发商早已悄悄降价，因无相关城市房产价格季度报而不被察觉。一线城市部分楼盘抛售的现象，让市场出现了唱空“北、上、广”的声音。这些现象只能说明价格回落周期显现，部分泡沫被挤出，退出市场大潮，并不是一场全面的唱衰运动，此时视线更应该转向问题与潜在危机更为严重的中小城市房产泡沫，其随时可能破裂而诱发连锁反应，甚至波及区域中心城市。而一线城市的全域中心定位，让其有更充沛的抗压能力与消费能力，随着价格合理性回落，其存量房问题反而会得到缓解，价值属性更为突出（投资效率比更高）。

我们应该看到对于房产价格泡沫的挤出，并不是一场大城市攻坚战，而是一场周边城市防御战。从个体角度分析，最终房产泡沫的破灭并不意味着无房者有房可住、无力购买者消费得起房产，区域性中心城市的核心地段房产依旧是最好的投资保值对象。从全局角度分析，房地产业泡沫的破裂只会进一步强化核心区价值属性，反而对全面城市化、对中小城市发展起到抑制作用。新一届政府在承接上届政府的基础上，应适时、适度地对房地产业进行政策性调整（货币政策松动），避免房产行业系统性崩盘，诱发连锁性反应，抑制投资性需求对房价的催化剂作用——即上涨时助涨，下跌时助跌——使其恢复到常态化运行区间。

[1] 潘文卿.中国的区域关联与经济增长的空间溢出效应[J].经济研究, 2012, (01).

[2] 王鹤.基于空间计量的房地产价格影响因素分析[J].经济评论, 2012, (01).

[3] 沈体雁,冯等田,孙铁山.空间计量经济学[M].北京:北京大学出版社, 2010.

[4] 保罗·克鲁格曼.发展、地理学与经济理论[M].蔡荣译.北京:北京大学出版社,中国人民大学出版社, 2000.

[5] 藤田昌久,保罗·克鲁格曼,安东尼.J.维纳布尔斯.空间经济学——城市、区域与国际贸易[M].梁琦主译.北京:中国人民大学出版社, 2011.

[6] Michael J.de Smith,Michael F.Goodchild,Paul A.Longley.地理空间分析——原理、技术与软件工具[M].(第二版).杜培军,张海荣,冷海龙等译.北京:电子工业出版社, 2009.

[7] 李婧,谭清美,白俊红.中国区域创新生产的空间计量分析——基于静态与动态空间面板模型的实证研究[J].管理世界,2010, (07).

[8] 吕健.城市化驱动经济增长的空间计量分析: 2000～ 2009[J].上海经济研究, 2011, (05).