高精度SAR ADC非理想因素分析及校准方法
2015-12-22朱樟明梁宇华
曹 超,马 瑞,朱樟明,梁宇华,叶 谦
(西安电子科技大学微电子学院,陕西西安 710071)
高精度SAR ADC非理想因素分析及校准方法
曹 超,马 瑞,朱樟明,梁宇华,叶 谦
(西安电子科技大学微电子学院,陕西西安 710071)
对高精度逐次逼近型模数转换器的非理想因素进行理论推导和建模分析,表明模数转换器精度主要受电容失配和低位电容阵列及耦合电容的寄生电容影响,而高位寄生电容的影响可以忽略.建立了16位逐次逼近型模数转换器的高层次模型,验证了理论分析,并通过一种全数字的后台校准技术来减小电容失配和寄生电容的影响.仿真结果表明,校准后的有效位数在15位以上的概率超过90%.
高精度模数转换器;逐次逼近型模数转换器;电容失配;数字校准;高层次建模
逐次逼近型模数转换器(Successive Approximation Register Analog-to-Digital Converters,SAR ADC)具有结构简单、功耗低、面积小、易集成等特点,是当前工业界和学术界的研究热点之一.由于逐次逼近型模数转换器不需要运算放大器,使得逐次逼近型模数转换器比其他奈奎斯特模数转换器更适合现代互补金属氧化物半导体(Complementary Metal Oxide Semiconductors,CMOS)工艺的演进路线[1].逐次逼近型模数转换器中的数模转换器(Digital-to-Analog Conventer,DAC)通常是由二进制权重的电容阵列实现的,电容失配是限制逐次逼近型模数转换器精度的主要因素之一[2].如果没有校准,逐次逼近型模数转换器能够得到的最大精度是12位[3].对于12位以上的精度,需要校准技术来降低电容失配的影响.CMOS器件尺寸按比例缩小使得数字校准方法具有很大的优势.
文献[4]采用电阻电容混合数模转换器结构,提出自校准技术,通过额外的电阻串数模转换器校准电容失配.校准阶段计算并存储误差值,并在模数转换器正常工作时将其加入累加寄存器中得到正确的结果,校准后得到15位的精度.文献[5]基于自校准技术,改用额外的电容阵列数模转换器实现校准.数字校准的优势使其日渐成为校准技术的主流[6-11].文献[6]采用非二进制电容数模转换器结构提出了基于扰动的数字后台校准.文献[7]采用“Split模数转换器”结构对逐次逼近型模数转换器进行全数字后台校准.文献[8]采用“Dithering”的数字校准技术来消除失配的影响.笔者提出了一种16位逐次逼近型模数转换器的数字校准行为级模型,分析了寄生电容和电容失配对逐次逼近型模数转换器精度的影响,并采用了一种全数字后台校准方法.
1 16 位逐次逼近型模数转换器结构
传统的电荷再分配逐次逼近型模数转换器的数模转换器采用二进制权重的电容阵列,N位的电容值为2N,随N呈指数增加,会增大芯片的面积,降低转换速度.常见的解决办法是采用分段电容阵列结构[9-10],它把一个二进制电容阵列分成两个子二进制电容阵列,通过耦合电容把两个电容阵列连接起来.16位逐次逼近型模数转换器结构如图1所示.
图1中电容C是耦合电容,最低有效位(Least Significant Bit,LSB)是低八位电容阵列,右边是冗余电容C0和高八位电容阵列最高有效位(Most Significant Bit,MSB).传统结构中冗余电容C0在低位电容阵列,耦合电容C值是个分数,在版图中很难实现匹配,降低了精度.在笔者的设计中,耦合电容C为单位电容,把冗余电容C0放在了高位电容阵列.以比较器正向输入端的电容阵列为例来说明其具体工作过程.在采样阶段,只有高位进行采样,高位电容和冗余电容的下极板接输入信号Vin,上极板接共模电平Vcm,低位电容下极板都接地.在保持阶段,所有电容下极板接地,Vcm从电容上极板断开,此时可得

然后将电荷重新分配.首先是最高位电容接基准电压VREF,比较器进行比较.如果输出为高电平,最高位电容接地,次高位接VREF,然后进行第2位比较.依次进行,直到比较完最后一位,逐次逼近过程结束并有

其中,Di是电容阵列的开关逻辑控制信号.如果Di=0,则该电容接地;反之,则该电容接VREF.
2 寄生电容和电容失配对精度的影响
逐次逼近型模数转换器的精度主要是由任意两电容之间的比例决定的,电容之间的失配可以通过校准来解决[11].如果考虑到寄生电容的影响,模数转换器的性能会进一步下降[12-14].带有寄生电容的电容阵列电路如图2所示,Cpi(i=1~8)和Cpc分别表示电容Ci和耦合电容的寄生电容,电容CpMSB和CpLSB分别表示最高有效位和最低有效位电容阵列所有电容上极板寄生电容之和.
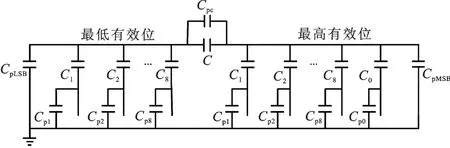
图2 带有寄生电容的电容阵列示意图
这里分析电容下极板寄生电容的作用.在转换过程中,电容的下极板不是接地就是接基准电压,所以下极板寄生电容对电荷的重新分配没有任何影响,模数转换器的线性特性不受影响,只不过增加了功耗.
下面只考虑最高有效位电容阵列上极板寄生电容CpMSB的影响.当逐次逼近过程结束时,式(2)变成了
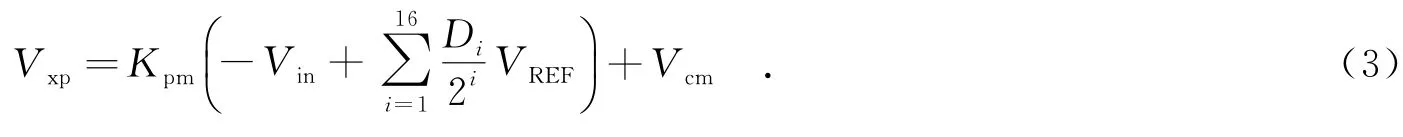
从式(3)可知,CpMSB对电容阵列数模转换器的输出没有影响,整个模数转换器的线性特性保持不变.与式(2)相比,系数Kpm比系数K更小,对比较器的精度提出了更高的要求.若只考虑最低有效位电容阵列寄生电容CpLSB的影响时,

由式(4)可知,CpLSB的影响使得低位电容阵列比较时模数转换器的输出产生了增益误差,而最高有效位电容阵列比较时不存在增益误差,会产生一定的非线性影响精度,从而使模数转换器的有效位数下降.同理可得耦合电容的寄生电容Cpc的影响:
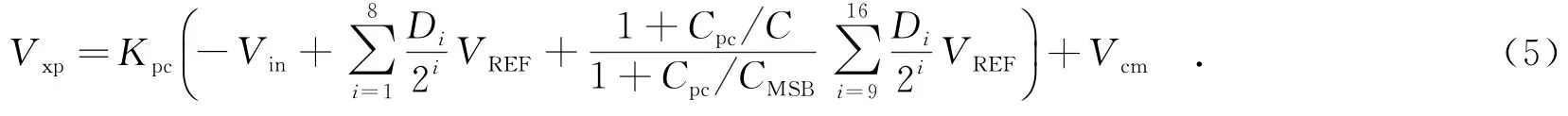
式(5)表明,Cpc和CpLSB一样引起了最低有效位电容的增益误差,造成了非线性.上式中,
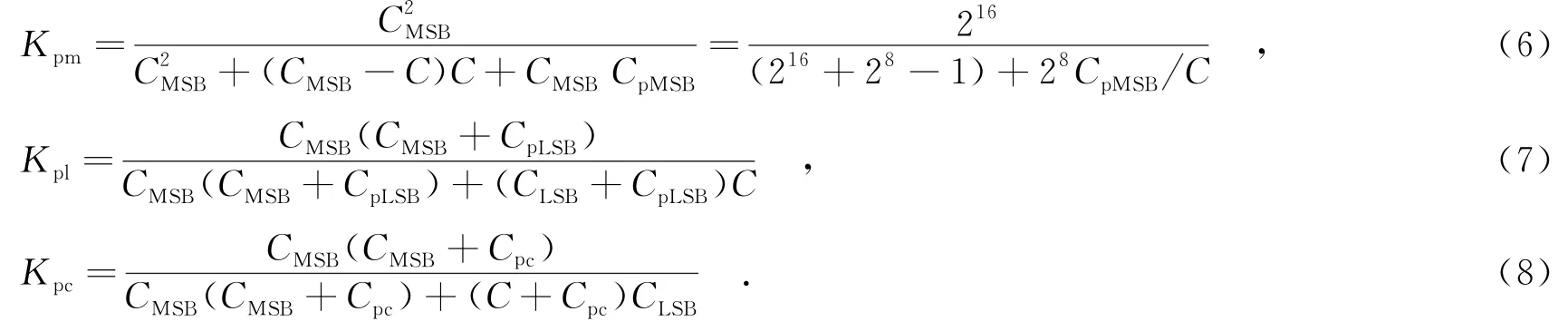
电容失配也是限制精度的主要因素之一.在模数转换器的统计模型中,假设单位电容服从均值为C0、标准差为δ的正态分布,其他电容由单位电容并联组成.差分非线性(Differential Non-Linearity,DNL)的方差约为[12]

其中,BLSB表示最低有效位.要求3σDNL<0.5BLSB,可得16位精度下,在现有的工艺下无法实现,需要校准技术.
3 数字校准技术
对于12位以上的逐次逼近型模数转换器,必须采用校准技术.传统模拟校准技术需要额外的模拟电路,增加了电路的复杂度[4,15].最近出现了一些数字校准技术[16-17],能更好地利用工艺尺寸不断缩小带来的优势.笔者采用了一种全数字后台校准方法,其校准原理如图3所示[7].
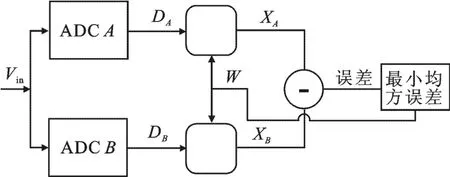
图3 数字校准方法的原理图
图3中模数转换器“A”是要校准的逐次逼近型模数转换器,模数转换器“B”是另一个带有失配的逐次逼近型模数转换器,两个模数转换器相互独立,同时对输入信号Vin采样.每个模数转换器都对Vin进行转换,产生各自的数字输出码DA和DB.
考虑电容失配,假设最后电压Vxp变为Vcm,D1为最高位数字输出,D16为最低位数字输出.以x代表VinVREF:

由于实际电路中存在电容失配,电容权重Wi不是准确的1/2i序列.如果用数字域估计的权重值W′i= Wi+εi来代替模拟域的权重值Wi,可以得到数字域校正值,即

对模数转换器“A”和“B”的权重估计值分别为

在式(12)和(13)中,第1项表示正确的x值,因为两个模数转换器转换相同的输入信号,所以x值相等.第2项表示各自的误差,“A”和“B”输出的差值即为误差值.如果误差εiA和εiB最后足够小,x′iA和x′iB将接近正确的x值.

根据误差值,通过最小均方根(Least Mean Square,LMS)迭代算法,不断更新“A”和“B”的权重值.

其中,μe是一个系数,控制迭代算法的速度和精度.该校准算法在后台不断进行,当误差足够小时认为校准完成.
4 仿真验证与讨论
通过Matlab完成行为级建模并对算法进行仿真验证.首先检验高位电容阵列寄生电容CpMSB的影响,假设CpMSB的值为最高有效位总电容CMSB的10%,充分考虑行为级建模与实际的偏差,为了留有足够的裕量,在采样率为1 MS/s、输入信号频率为473.6 k Hz时,有效位数(Effective Number Of Bits,ENOB)为15.99位.
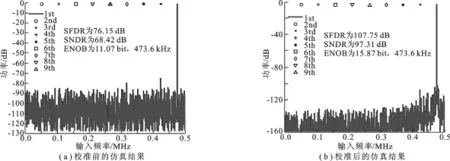
图4 数字校准技术验证
所以,只要比较器精度足够高,CpMSB的影响完全可以忽略.在相同假设下,考虑CpLSB的影响,有效位数为11.48位;考虑Cpc的影响,有效位数为11.45位.因此,Cpc和CpLSB一样,使有效位数显著降低.仿真结果与式(4)和式(5)描述的一致.
假设电容失配为0.5%,同时考虑上述寄生效应,仿真结果如图4所示.校准前有效位数为11.07位,校准后有效位数为15.87位,表明该校准方法能够很好地对逐次逼近型模数转换器的各种非理想因素进行校准.
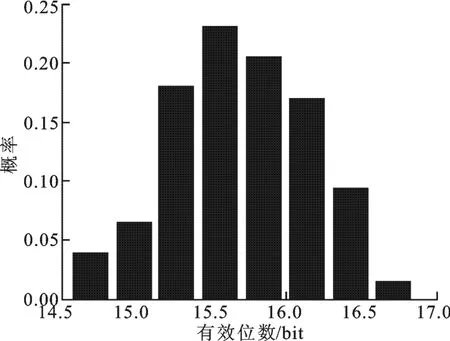
图5 200次仿真的有效位数概率分布图
为了更好地说明该校准方法的可行性,笔者进行了200次仿真验证,得出校准后的有效位数与其概率的分布图,如图5所示.校准后的有效位数在15位以上的概率达到90%以上,最低有效位数是14.5位,说明该数字校准技术能很好地实现高精度逐次逼近型模数转换器的校准.
5 总 结
笔者详细分析了分段逐次逼近型模数转换器中各种非理想因素对精度的影响,表明影响分段模数转换器精度的主要因素是电容失配、低位电容阵列的寄生电容及耦合电容的寄生电容,高位寄生电容对模数转换器的影响可以忽略,并通过Matlab行为级模型验证了这一结论.同时,将一种数字后台校准方法用于分段逐次逼近型模数转换器,对于较大的失配和寄生电容,通过行为级仿真验证了该校准的有效性.
[1] 杨银堂,李迪,石立春,等.一种用于14位1.28 MS/sΣADC的数字抽取滤波器设计[J].西安电子科技大学学报,2010,37(2):315-319. Yang Yintang,Li Di,Shi Lichun,et al.Decimation Filter Design for 14-bit 1.28 MS/s Sigma-delta ADC[J].Journal of Xidian University,2010,37(2):315-319.
[2] 佟星元,杨银堂,朱樟明,等.逐次逼近ADC无源器件的匹配性与高层次模型[J].西安电子科技大学学报,2011,38 (6):123-129. Tong Xingyuan,Yang Yintang,Zhu Zhangming,et al.Mismatch Analysis and High-level Modeling of Passive Components in Successive Approximation A/D Converters[J].Journal of Xidian University,2011,38(6):123-129.
[3] 佟星元,陈杉,蔡乃琼,等.一种R-C-R组合式12位逐次逼近A/D转换器[J].西安电子科技大学学报,2010,37 (5):904-910. Tong Xingyuan,Chen Shan,Cai Naiqiong,et al.12-bit SAR A/D Converter with an R-C-R Hybrid Architecture[J]. Journal of Xidian University,2010,37(5):904-910.
[4]Lee H S,Hodges D A,Gray P R.A Self-calibrating 15 bit CMOS A/D Converter[J].IEEE Journal of Solid-state Circuits,1984,19(6):813-819.
[5]Chang A H,Lee H S,Boning D.A 12b 50 MS/s 2.1 mW SAR ADC with Redundancy and Digital Background Calibration[C]//Proceedings of the 39th European Solid-state Circuit Conference.Piscataway:IEEE,2013:109-112.
[6]Liu W,Huang P,Chiu Y.A 12-bit,45-MS/s,3-mW Redundant Successive-approximation-register Analog-to-digital Converter with Digital Calibration[J].IEEE Journal of Solid-state Circuits,2011,46(11):2661-2672.
[7]Mc Neill J,Chan K Y,Coln M C W,et al.All-digital Background Calibration of a Successive Approximation ADC Using the“Split ADC”Architecture[J].IEEE Transactions on Circuits and Systems:Regular Papers,2011,58(10):2355-2365.
[8]Xu R,Liu B,Yuan J.Digitally Calibrated 768-kS/s 10-b Minimum-size SAR ADC Array with Dithering[J].IEEE Journal of Solid-state Circuits,2012,47(9):1-11.
[9]Um J Y,Kim Y J,Song E W,et al.A Digital-domain Calibration of Split-capacitor DAC for a Differential SAR ADC without Additional Analog Circuits[J].IEEE Transactions on Circuits and Systems:Regular Papers,2013,60(11): 2845-2856.
[10]Wang G,Kacani F,Chiu Y.IRD Digital Background Calibration of SAR ADC with Coarse Reference ADC Acceleration [J].IEEE Transactions on Circuits and Systems:Express Briefs,2014,60(1):11-15.
[11]Osipov D,Bocharov Y.Behavioral Model of Split Capacitor Array DAC for Use in SAR ADC Design[C]//Proceedings of the 8th Conference on Philosophiae Doctor Research in Microelectronics and Electronics.Piscataway:IEEE,2012:1-4.
[12]Chen Y.Split Capacitor DAC Mismatch Calibration in Successive Approximation ADC[J].IEICE Transactions on Electronics,2010,93(3):295-302.
[13]Saberi M,Lotfi R,Mafinezhad K,et al.Analysis of Power Consumption and Linearity in Capacitor Digital-to-analog Converters Used in Successive Approximation ADCs[J].IEEE Transactions on Circuits and Systems:Regular Papers,2011,58(8):1736-1748.
[14]Cao T V,Aunet S,Ytterdal T.A 9-bit 50MS/s Asynchronous SAR ADC in 28nm CMOS[C]//2012 NORCHIP Conference.Washington:IEEE Computer Society,2012:6403105.
[15]Mueller J H,Strache S,Busch L,et al.A Calibratable Capacitance Array Based Approach for High Resolution CR SAR ADCs[C]//Proceedings of the 19th International Conference on Mixed Design of Integrated Circuits and Systems. Piscataway:IEEE,2012:183-188.
[16]Li Z,Lu Y X,Mo T T.Calibration for Split Capacitor DAC in SAR ADC[C]//Proceedings of the 10th International Conference on ASIC.Washington:IEEE,2013:1-4.
[17]Sun L,Dai Q Y,Qiao G S.Analysis on Capacitor Mismatch and Parasitic Capacitors Effect of Improved Segmentedcapacitor Array in SAR ADC[C]//Proceedings of the 3rd International Symposium on Intelligent Information Technology Application.Piscataway:IEEE Computer Society,2009:280-283.
(编辑:郭 华)
Analysis of non-ideal factors and digital calibration for highresolution SAR ADCs
CAO Chao,MA Rui,ZHU Zhangming,LIANG Yuhua,YE Qian
(School of Microelectronic,Xidian Univ.,Xi’an 710071,China)
An analysis of capacitor mismatch in a high resolution successive approximation register(SAR) analog-to-digital converter(ADC)is described.The results show that the mismatch of capacitors and the parasitic capacitance in the LSB capacitor array have a significant influence on the resolution of ADC while the parasitic one in MSB array has little influence on the precision.A 16-bit SAR ADC high-level model is designed and a background digital calibration is proposed to calibrate the errors due to the mentioned sources.Simulation results indicate that the ENOB(Effective number of bits)after calibration is above 15 bit with a probability of more than 90%.The availability of this calibration method is verified,so it can be utilized to calibrate high-resolution SAR ADC.
high resolution analog-to-digital converters;successive approximation register analog-todigital converters;capacitor mismatch;digital calibration;high-level model
TN431.2
A
1001-2400(2015)06-0061-05
10.3969/j.issn.1001-2400.2015.06.011
2014-10-17
时间:2015-03-13
国家自然科学基金资助项目(61234002,61322405,61306044,61376033)
曹 超(1988-),男,西安电子科技大学博士研究生,E-mail:chao_cao@126.com.
http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.011.html
