稳健的二级嵌套阵列自适应波束形成算法

杨 杰,廖桂生,李 军

(西安电子科技大学雷达信号处理国家重点实验室陕西西安710071)

稳健的二级嵌套阵列自适应波束形成算法

杨 杰,廖桂生,李 军

(西安电子科技大学雷达信号处理国家重点实验室陕西西安710071)

针对信号模型失配情形下的二级嵌套阵列波束形成问题,提出一种基于干扰-噪声协方差矩阵高效重构和半定规划的稳健自适应波束形成算法.该算法首先利用接收信号的对角增长曲线模型,并结合无需空域搜索的ESPRIT方法,精确重构虚拟阵列的干扰-噪声协方差矩阵;其次,利用干扰-噪声协方差矩阵和少量先验信息构造稳健自适应波束形成中的优化问题,有效减小了传统最小方差无失真响应波束形成器在非理想信号环境中的性能损失;最后,采用半定松弛方法得到该优化问题的近似表达形式,即半定规划问题,并借助凸优化工具包求解.仿真结果表明,在不同的输入信噪比和采样快拍数情形下,该算法与现有算法相比,具有更高的输出信干噪比.

二级嵌套阵列;稳健自适应波束形成;干扰-噪声协方差矩阵重构;半定规划;半定松弛

自适应波束形成作为阵列信号处理的一个主要研究方向,在无线通信、雷达、声纳、射电天文及医学成像等领域得到广泛应用.实际应用场景中,由于存在波达方向（Direction Of Arrival,DOA)误差、阵列结构误差等模型失配因素,导致传统最小方差无失真响应（Minimum Variance Distortionless Response,MVDR)波束形成器性能损失严重.基于此,一些稳健自适应波束形成算法[1-5]被先后提出,如对角加载方法[1]、子空间方法[2]、优化最差性能方法（worst-case方法)[3]、连续二次规划（Sequential Quadratic Programming,SQP)方法[4]等.较之传统MVDR波束形成算法,稳健自适应波束形成算法能有效提高模型失配情形下的阵列输出信干噪比（Signal to Interference and Noise Ratio,SINR).然而,此类算法仍存在用户参数选取困难、先验信息需求较高和干扰-噪声协方差矩阵未精确重构等缺点.

二级嵌套阵列[6-7]是近年来提出的一种新型阵列结构,与具有相同物理阵元数目（设为N)的均匀线阵相比,嵌套阵列可通过虚拟变换使自由度扩展至O（N2).因此,在自适应波束形成算法中,利用二级嵌套阵列能够抑制数目多于物理阵元总数的干扰信号.文献[6]研究了二级嵌套阵列的自适应波束形成算法,该算法仅适用于预设信号模型与实际信号模型相匹配的情况,若信号模型失配,则该算法性能急剧恶化.因此,关于二级嵌套阵列稳健自适应波束形成算法的研究有必要进行开展.

笔者在文献[6]研究成果的基础上,提出一种二级嵌套阵列的稳健自适应波束形成算法.该算法首先利用基于旋转不变特性的信号参数估计（Estimating Signal Parameters via Rotational Invariant Technique,ESPRIT)技术和接收数据的对角增长曲线（Diagonal Growth Curve,DGC)模型[8]精确重构虚拟阵列的干扰-噪声协方差矩阵;其次,利用干扰-噪声协方差矩阵和少量先验信息构造优化问题,以求解真实的期望信号导向矢量;最后,利用半定松弛方法将待求解的非凸优化问题转化为半定规划问题,并采用凸优化工具包求解.理论分析与仿真结果表明,笔者提出的干扰-噪声协方差矩阵重构算法具有比文献[9]中算法更快的运算速度和更高的重构精度,在不同的输入信噪比和采样快拍数情形下,该算法具有比传统算法更高的输出SINR.

1 二级嵌套阵列信号模型

二级嵌套阵列的物理结构如图1所示,图中d表示接收信号载波波长的一半.由图1可知,二级嵌套阵列由两组不同尺寸的均匀线阵组成,其中第一组均匀线阵（即第1级)包含M个阵元,阵元间距为d;第2组均匀线阵（即第2级)包含N个阵元,阵元间距为（M+1)d.假设K个来自空间不同方向θi（i=1,2,…,K)的远场窄带平面波信号入射到二级嵌套阵列上,则输出信号的表达形式为

图1 二级嵌套阵列物理结构图

其中,y（t)=[y1（t),y2（t),…,yM+N（t)]T,表示所有阵元在采样时刻t的输出信号;A=[a（θ1),a（θ2),…,a（θK)],表示所有入射信号DOA对应的阵列流形矩阵,a（θ)表示θ对应的导向矢量;s（t)=[s1（t),s2（t),…,sK（t])T,表示采样时刻t由所有入射信号组成的矢量;n（t)[ =n1（t),n2（t),…,nM+N（t]),表示所有阵元接收到的高斯噪声向量,其均值为0,方差为

假设不同入射信号的波形之间互不相关,则由式（1)可得接收信号的协方差矩阵为

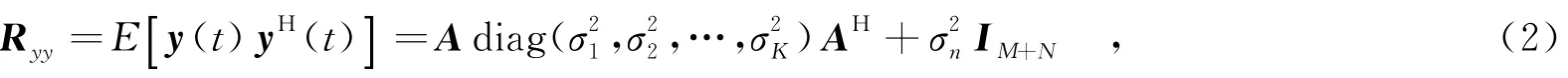
其中,E[·]表示求期望操作,diag（·)表示求对角矩阵操作,表示各个入射信号的功率,IM+N表示（M+N)×（M+N)维的单位矩阵.

将式（2)中的协方差矩阵按列排成如下向量形式:

式（3)经过去冗余元素和向量重排操作[6],可得如下表达式:

其中,A1等效于阵元位置坐标集合为{md,m=-D,-D+1,…,D,D=N（M+1)-1}的虚拟阵列流形矩阵,e表示中心元素为1,其余元素为0的（2D+1)×1维列向量.

式（4)等效为单快拍信号,其协方差矩阵的秩为1,无法直接应用于MVDR波束形成器中.采用文献[6]提出的空间平滑算法,可得如下平滑协方差矩阵:

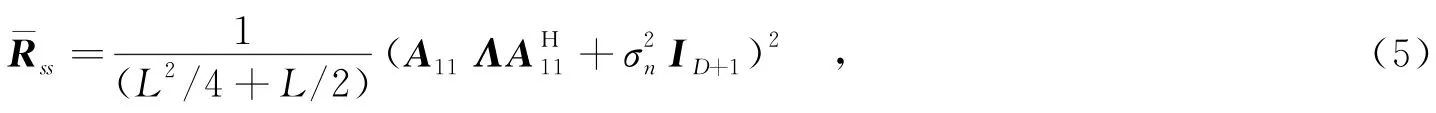
其中,L=M+N;A11表示（D+1)×K维的阵列流形矩阵,其对应的虚拟阵元位置坐标集合为{md,m=0,1,…,D};表示（D+1)×（D+1)维的单位矩阵.

在二级嵌套阵列中,定义虚拟阵列对应的接收信号协方差矩阵为

其中,β=L2/4+L/2.

假设期望信号的DOA为θ0,则由式（6)可得虚拟阵列对应的MVDR波束形成器权矢量为[6]

其中,b（θ0)表示（D+1)×1维的期望信号导向矢量.

由式（7)可知,该MVDR波束形成器可利用的自由度为D+1,由于D＞（M+N),故采用如上信号处理方法可抑制数目多于物理阵元数的干扰信号,这是相同物理阵元数的均匀线阵MVDR波束形成器无法达到的效果.该结论可由图2所示阵元总数为6的二级嵌套阵列MVDR方向图验证.图2中,干扰信号方向如箭头所指,期望信号方向为0°,信噪比（Signal Noise Ratio,SNR)为10 d B,干噪比（Interference and Noise Ratio,INR)为30 dB.

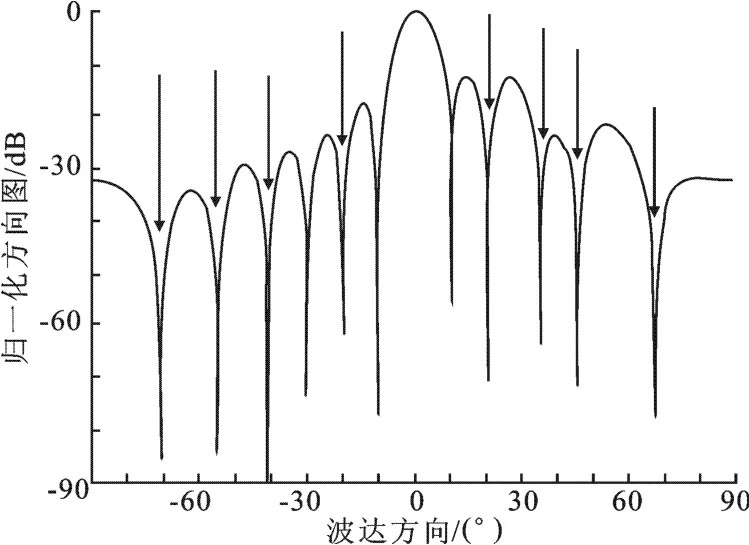
图2 二级嵌套阵列MVDR波束方向图

2 二级嵌套阵列稳健波束形成算法

2.1 高效干扰-噪声协方差矩阵重构方法

理想自适应波束形成器的采样协方差矩阵应仅含干扰和噪声信号,然而,由于实际应用中快拍数据内往往混杂有期望信号,因而理想干扰-噪声协方差矩阵无法得到.在信号模型失配情形下,利用此非理想协方差矩阵进行自适应波束形成,会导致高信噪比下的期望信号相消现象.为解决上述问题,文献[9]提出一种基于Capon谱估计的干扰-噪声协方差矩阵重构方法.然而,此方法需对空域进行遍历搜索,计算复杂度较大,同时,与信号功率和DOA的真实值相比,利用该方法得到的估计值精度较低.针对上述问题,文中提出一种高效重构算法.该算法首先利用ESPRIT算法精确估计入射信号DOA;其次,利用DOA估计结果和接收信号的DGC模型,精确估计入射信号幅度;最后,利用非期望信号区域内的DOA和幅度估计值,重构干扰-噪声协方差矩阵.与文献[9]算法相比,ESPRIT算法无需空域搜索即可确定信号DOA,因此运算复杂度较低,同时估计精度得到提高.利用DGC模型估计信号幅度,其精度也明显高于文献[9]的结果.文中算法的具体描述如下.

为利用ESPRIT算法估计信号DOA,需对式（4)所示的单快拍相干数据进行如下预平滑处理:首先,将虚拟阵列划分为L2/4+L/2个子阵列,其中,第i个子阵列对应的阵元位置坐标集合和阵列接收数据分别为{（-i+1+n)d,n=0,1,…,L2/4+L/2-1}和zi,zi表示由z中的第（L2/4+L/2-i+1)个元素至第（（L2-2)/2+L-i+1)个元素组成的向量;然后,将每个子阵列划分为两个阵元数均为L2/4+L/2-1的子阵列,得到其接收信号形式^zi=[z1i,z2i]T,其中,z1i和z2i分别表示由zi的前L2/4+L/2-1行和后L2/4+ L/2-1行元素组成的向量;最后,按下式计算平滑协方差矩阵:

由式（1)可得接收信号的DGC模型为[8]

其中,Y、S和N分别表示由所有观测时间内积累的快拍数据组成的接收信号矩阵、信号波形矩阵和噪声矩阵;Γ=diag（σ1,σ2,…,σK).

根据式（9)及文献[8]提出的近似最大似然（Approximate Maximum Likelihood,AML)算法,可得入射信号的幅度估计值为

其中,A由DOA估计值和阵列物理结构得到;Φ=Y（I-PS)YH,I表示单位矩阵,PS=SH（SSH)+S,（·)+表示求广义逆矩阵操作;⊕表示求Hadamard积操作;vecd（·)表示求矩阵对角向量操作,即取出矩阵中的对角元素组成向量.

由式（9)和式（10),可得干扰-噪声协方差矩阵的表达式为

容易知道,文献[9]中重构算法的运算复杂度为O（（D+1)2J),其中,J表示空域采样点数.文中所提重构算法的运算复杂度为O（（D+1)3),由于J≫D,因此,文中算法的计算复杂度较低.

图3所示为空间3个非相干信号入射到六阵元二级嵌套阵列时,文中算法与文献[9]算法重构出的信号幅度谱图,其中,信号的真实DOA和幅度由空心圆圈对应的坐标表示.由图3可知,文中算法的参数估计精度较高.

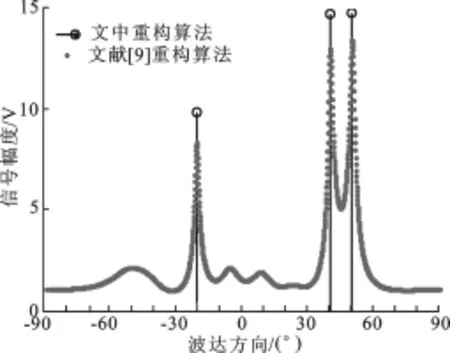
图3 不同算法重构出的信号幅度谱图

2.2 基于半定规划的稳健波束形成算法

以式（11)所得矩阵R替代接收信号采样协方差矩阵,可得信号模型失配情形下,二级嵌套阵列中稳健波束形成问题的表达形式为

其中,w表示波束形成权矢量,b表示预设的虚拟阵期望信号导向矢量,未知向量e表示虚拟阵中真实期望信号导向矢量与预设期望信号导向矢量之间的误差.

与求解MVDR波束形成器权矢量的过程类似,易知式（12)所示优化问题的解为

其中,α=1(/（b+e)HR-1（b+e)).将w代入式（12)的目标函数中,易知稳健波束形成器的输出功率为

下面建立一组优化问题并使其解向量p比较精确地拟合于真实期望信号导向矢量b+e.其构造思路为:在保证式（14)所示输出功率P最大化（即pHR-1p最小化)的前提下,限制p的取值范围,避免其扩散到干扰信号空间.各约束条件的具体描述如下.

不失一般性,假设期望信号所在空间区域Θ及阵列物理结构等先验信息已知（实际阵列物理结构可能与已知信息存在偏差).现定义如下正定矩阵:

对式（15)中的F进行特征分解,可得

其中,Λ1表示由F的K′个大特征值组成的对角矩阵,K′表示干扰信号总个数,U1表示Λ1对应的特征向量矩阵,Λ2表示由F的D+1-K′个小特征值组成的对角矩阵,U2表示Λ2对应的特征向量矩阵.

由于式（15)中F的积分区间为干扰信号所在空域,故由式（16)可知:若θ∈Θ,则q（θ)≈U2f2;若θ∈,则q（θ)≈U1f1.其中f1和f2为相应的拟合向量.根据,易知:下面定义Δ=qH（θ)Fq（θ),则.由式（16)中Λ1和Λ2的定义易知,Δ在期望信号空域内取值较小,在干扰信号空域内取值较大.令,则通过如下约束条件可使p收敛于Θ对应的导向矢量空间,即

在满足式（17)所示准则的基础上,需进一步考虑降低干扰信号所在空域内的波束方向图增益.将p代入式（13),可得波束形成权矢量（忽略常数因子)R-1p,据此可计算出内某点的波束方向图增益为pHR-1q（θ)qH（θ)R-1p（θ∈).将之推广到全域,可得旁瓣增益的限制条件为

其中,γ表示可容忍的旁瓣增益上界.

经过如上分析,易知文中所提稳健波束形成算法可表述为如下优化问题:

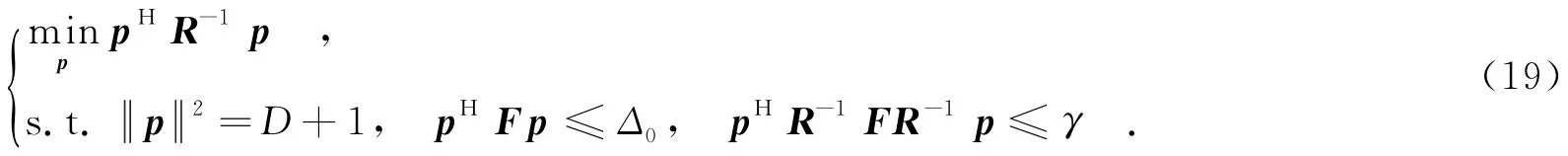
令B=p pH,由矩阵迹的性质易知:pHR-1p=tr（R-1B),,pHFp=tr（FB),pHR-1FR-1p=tr（R-1FR-1B),其中,tr（·)表示求矩阵迹操作.利用上述变换可将式（19)改写为

其中,rank（·)表示求矩阵秩操作.需要注意,由于ran k（B)=1,为非凸约束条件,式（20)所示的优化问题是非凸的.采用文献[10-11]提出的半定松弛方法,可将式（20)转化为如下凸优化问题:

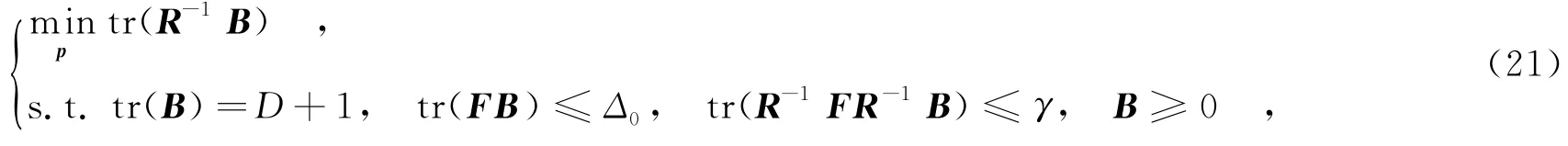
其中,B≥0,表示B为半正定矩阵.式（21)所示的半定规划问题可通过现有的凸优化工具包（如CVX)求解.需要注意,与原问题式（20)相比,求解问题式（21)所得的松弛解可能不是全局最优的（如ran k（B)≠1),此时,可采用文献[10]提出的随机选择方法得到全局最优解.此外,式（21)中的用户参数γ可由如下半定规化问题的解确定:

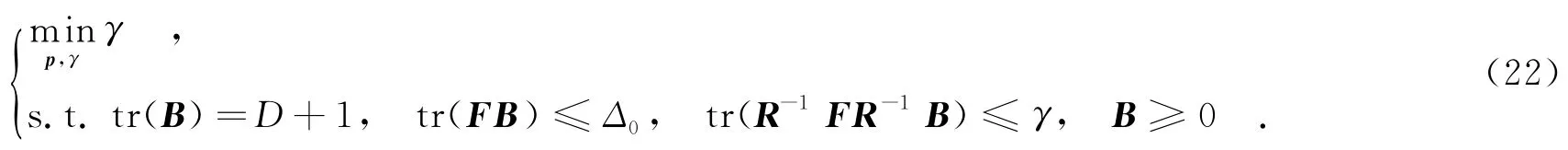
对比式（21)与式（22)可知,二者约束条件相同.因此,若使γ≥γmin（γmin表示式（22)的最优解),则可在保证式（21)可行解存在的前提下,最大程度地压低旁瓣增益.同时易知文中算法利用的先验信息较少（仅需已知Θ和粗略的阵列物理结构,而传统算法需已知对角加载因子、误差向量e的范围和噪声子空间维数等信息).

3 仿真结果与分析

通过计算机仿真对比分析不同信号模型失配情形下,文中算法和传统算法的波束形成性能.假设二级嵌套阵列阵元总数为6（其第1级和第2级的阵元数分别为3),各阵元位置坐标易由图1所示的阵列物理结构推得.来自空间不同方向的远场窄带信号互不相关,而其与加性高斯白噪声也不相关.期望信号DOA的预设值为5°,空域变化范围Θ=[0°,10°],两个干扰信号的DOA分别为40°和60°,干噪比均为30 d B.在对角加载方法中,对角加载因子取为2σ2n;在子空间方法和SQP方法中,噪声子空间维数假设已知;在worst-case方法中,误差向量e的上界取为0.3（D+1).各仿真中蒙特卡洛试验次数均设为200.

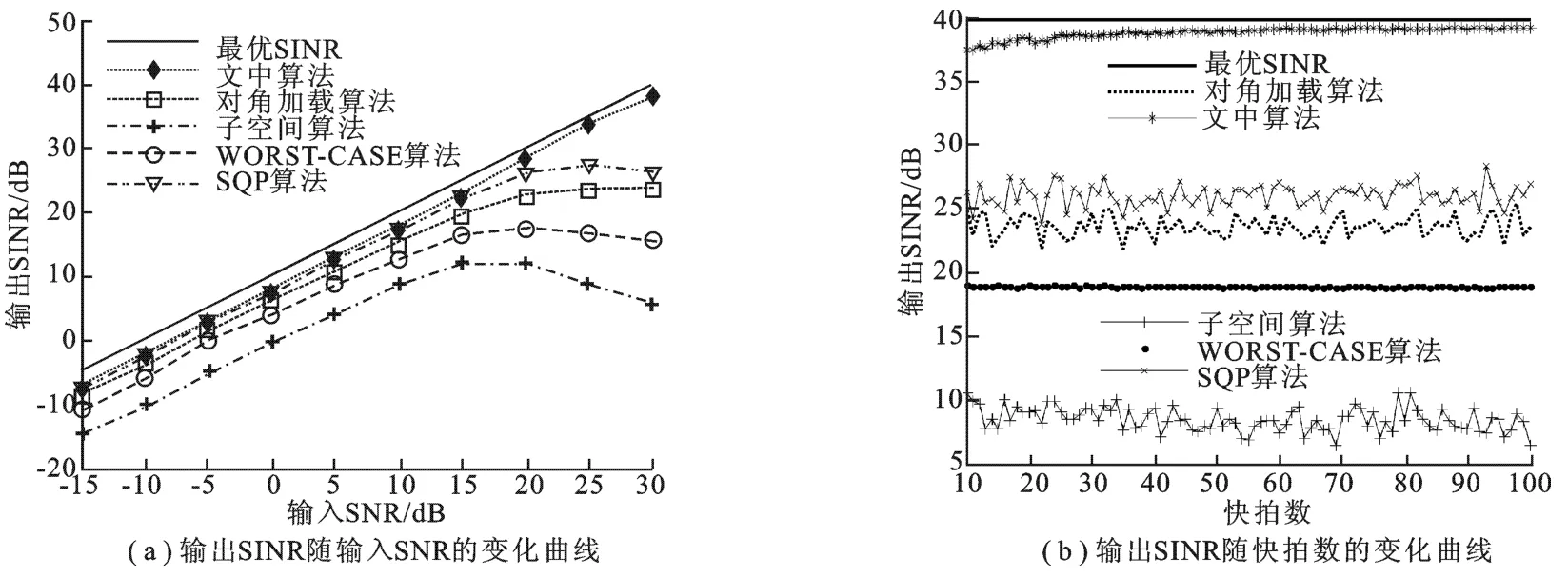
图4 相干散射模型下各算法性能对比图

由图4所示仿真结果可知,应用文中算法所得的阵列输出SINR曲线最接近最优输出SINR曲线.这是由于与传统算法相比,文中算法可精确估计真实的期望信号导向矢量（传统算法由于不能获得完备准确的先验信息,因而估计精度较低).由图4所示子空间方法的输出SINR曲线可知,在低输入SNR和小采样快拍数情形下,该方法的性能最差.这是由于在上述条件下,噪声子空间与信号子空间发生混叠,导致接收数据无法投影到理想的信号子空间.由图4（a)所示的各传统算法的输出SINR曲线可知,在输入SNR较高时各算法性能逐渐恶化.这是由于在此条件下,采样协方差矩阵中期望信号占比较大,然而由于期望信号的先验信息与真实信息间存在误差,故此时各算法对期望信号的抑制效应增强,造成期望信号相消现象.

仿真2 各算法对阵列结构误差和信号DOA误差的稳健性分析.仿真中考虑由阵元位置误差和信号DOA误差引起的信号模型失配现象.在不同蒙特卡洛实验中,各阵元的位置误差相互独立且均服从[-0.1λ,0.1λ]（λ表示信号载波波长)区间的均匀分布,期望信号DOA服从均值为5°、方差为2°的高斯分布.图5（a)为快拍数固定为30时,各算法的阵列输出SINR随输入SNR变化的曲线;图5（b)为输入SNR固定为30dB时,各算法的阵列输出SINR随快拍数变化的曲线.

图5 存在阵元误差和DOA误差时各算法性能对比图

与仿真1的结果类似,由图5所示各算法性能曲线的对比效果可知,文中算法具有最优的波束形成性能,同时图5（a)的仿真结果也可说明,随着输入SNR的增加,文中算法的输出SINR不会如传统算法般逐渐降低.对仿真2结果的分析如仿真1中所述,这里不再赘述.

4 结束语

笔者提出一种基于干扰-噪声协方差矩阵高效重构和半定规划的二级嵌套阵列稳健自适应波束形成算法.该算法首先利用ESPRIT算法和接收信号的DGC模型分别估计干扰信号的DOA和功率,进而精确重构干扰-噪声协方差矩阵;其次,利用干扰-噪声协方差矩阵和少量先验信息构造相应的优化问题,以恢复真实的期望信号导向矢量;最后,利用半定松弛方法将所得优化问题转化为半定规划问题并借助凸优化工具包求解.与传统稳健波束形成算法相比,文中算法对先验信息的需求较低,并可有效消除高输入SNR下的期望信号相消现象.仿真结果验证了文中算法的有效性.

[1]Cox H,Zeskind R M,Owen M H.Robust Adaptive Beamforming[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1987,35(10):1365-1376.

[2]Feldman D D,Griffiths L J.A Projection Approach for Robust Adaptive Beamforming[J].IEEE Transactions on Signal Processing,1994,42(4):867-876.

[3]Vorobyov S A,Gershman A B,Luo Z Q.Robust Adaptive Beamforming Using Worst-Case Performance Optimization: a Solution to the Signal Mismatch Problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.

[4]Hassanien A,Vorobyov S A,Wong K M.Robust Adaptive Beamforming Using Sequential Quadratic Programming:an Iterative Solution to the Mismatch Problem[J].IEEE Signal Processing Letters,2008,15(1):733-736.

[5]Vorobyov S A.Principles of Minimum Variance Robust Adaptive Beamforming Design[J].Signal Processing,2013,93 (12):3264-3277.

[6]Piya P,Vaidyanathan P P.Nested Arrays:a Novel Approach to Array Processing with Enhanced Degrees of Freedom [J].IEEE Transactions on Signal Processing,2010,58(8):4167-4181.

[7]Piya P,Vaidyanathan P P.Nested Arrays in Two Dimensions,Part I:Geometrical Considerations[J].IEEE Transactions on Signal Processing,2012,60(9):4694-4705.

[8]Xu L Z,Stoica P,Li J.A Diagonal Growth Curve Model and Some Signal-processing Applications[J].IEEE Transactions on Signal Processing,2006,54(9):3363-3371.

[9]Gu Y J,Leshem A.Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.

[10]Luo Z Q,Ma W K,Anthony M C,et al.Semidefinite Relaxation of Quadratic Optimization Problems[J].IEEE Signal Processing Magazine,2010,27(3):20-34.

[11]Hu Z,Qiu R C,Browning J P,et al.A Novel Single-step Approach for Self-coherent Tomography Using Semidefinite Relaxation[J].IEEE Geoscience and Remote Sensing Letters,2014,11(1):114-118.

（编辑:齐淑娟)

Robust adaptive beamforming with the two level nested array

YANG Jie,LIAO Guisheng,LI Jun
(National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China)

For the beamforming problem in the two level nested array under the condition of signal model mismatch,this paper proposes a robust adaptive beamforming algorithm based on efficient interferenceplus-noise covariance matrix reconstruction and semi-definite programming(SDP).Firstly,by using the diagonal growth-curve(DGC)model of the received signal and the search-free ESPRIT method,we reconstruct the interference-plus-noise covariance matrix of the virtual array precisely;then,the interference-plus-noise covariance matrix and a little prior information are applied to construct the optimization problem in robust adaptive beamforming,which can effectively decrease the performance degradation of the traditional MVDR filter in nonideal signal circumstances;finally,the optimization problem can be approximately expressed as an SDP problem by using the SDP relaxation method,and we can resort to the convex optimization software to solve it.Simulation results demonstrate that the proposed method achieves a higher output SINR under different input SNRs or sampling snapshots circumstances as compared to traditional methods.

two level nested array;robust adaptive beamforming;interference-plus-noise covariance matrix reconstruction;semi-definite programming(SDP);SDP relaxation

TN958

A

1001-2400（2015)06-0030-07

10.3969/j.issn.1001-2400.2015.06.006

2014-10-10

时间:2015-03-13

国家973计划资助项目（2011CB707001);国家自然科学基金资助项目（61231027,61271292)

杨 杰（1989-),男,西安电子科技大学博士研究生,E-mail:yangjie_xidian@126.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.006.html