Alpha稳定分布噪声下数字调制识别新方法

刘明骞,李兵兵,石亚云

(西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071)

Alpha稳定分布噪声下数字调制识别新方法

刘明骞,李兵兵,石亚云

(西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071)

针对传统的Alpha稳定分布噪声下数字调制识别方法在低信噪比环境下识别性能较差的问题,提出了一种基于广义累积量和广义瞬时相位的数字调制信号识别的新方法.该方法首先构造广义累积量特征参数,并提取分数阶傅里叶变换的零中心归一化广义瞬时相位的谱密度最大值作为识别的特征参数,然后通过最小均方误差分类器和门限的设置来实现Alpha稳定分布噪声下数字调制信号的识别.仿真结果表明,在Alpha稳定分布噪声下,该方法不仅识别性能较好,而且计算复杂度较低.

调制识别;Alpha稳定分布噪声;广义累积量;广义瞬时相位;最小均方误差

数字调制识别是在给定的数字信号备择集中确定信号的调制方式的过程,在军事通信、民用通信等方面都具有重要的应用[1].在许多文献中所涉及的调制识别算法都假设加性噪声服从高斯分布.然而,大部分无线电波信道中的人为电磁噪声、自然噪声以及两者的联合噪声常常表现出非高斯性.研究发现,近年来很多学者将非高斯噪声建模为Alpha稳定分布模型[2-3].因此,研究Alpha稳定分布噪声环境下的数字调制信号的识别技术具有实际的工程意义.

目前,一些学者已展开了Alpha稳定分布噪声下数字调制信号识别的研究.文献[4]利用K-S检测算法对正交相移键控（Quadrature Phase Shift Keying,QPSK),16正交振幅调制（Quadrature Amplitude Modulation,QAM)和64QAM信号在Alpha稳定分布噪声下进行了识别,但该方法在低信噪比下识别性能不理想;文献[5]以信号相位的分形盒维数作为识别特征,对Alpha噪声下数字调制信号进行了识别,但该方法仅能在一定混合信噪比范围内适用且识别性能较差;文献[6-7]利用分数低阶循环谱的相干系数构造特征实现了Alpha稳定分布噪声下数字调制信号的识别,但该方法普适性较差;文献[8]提出了基于广义二阶循环谱的Alpha稳定分布噪声下数字调制信号方法,但该方法计算复杂度高;文献[9-10]的方法在信噪比小于10 d B时,识别性能不理想.

针对以上问题,笔者提出了一种适用于低混合信噪比环境的Alpha稳定分布噪声下数字调制信号识别新方法.该方法首先对信号进行非线性变换,将信号幅值映射到有限区间范围[8],然后提取基于分数阶傅里叶变换的零中心归一化广义瞬时相位谱密度最大值,广义二阶累积量和广义四阶累积量,最后通过利用最小均方误差准则分类器以及设置判决门限对5种常用数字调制信号进行识别.仿真结果表明,在混合信噪比大于-2 dB时,该方法的识别率接近100%.可见,在Alpha稳定分布噪声下,该方法是有效可行的.

1 信号模型

Alpha稳定分布噪声下信号模型为

其中,x（t)为接收信号,s（t)为发送信号,n（t)为Alpha稳定分布噪声.

通常情况下,用特征函数对Alpha稳定分布进行描述[9]:

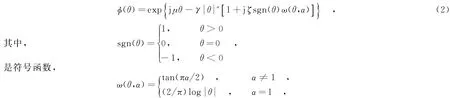
参数α（0＜α≤2)称为特征指数,γ≥0,为分散系数,ζ（-1≤ζ≤1)为对称参数,μ为位置参数.若能满足μ=0,且γ=1,则Alpha稳定分布称为标准的Alpha稳定分布.

2 Alpha稳定分布噪声下数字调制识别

2.1 广义累积量

首先根据载波频率和带宽[11],对信号进行频谱搬移,得到其等效基带信号,并对该信号进行功率归一化处理,从而得到基带信号y（t)=A exp（jϕ),其中A为信号幅度,,ϕ为信号的相位.对于基带信号y（t),根据共轭位置的不同,定义两种广义二阶累积量,其表达式为

其中,E表示期望,f（·)为一种非线性变换,可表示为

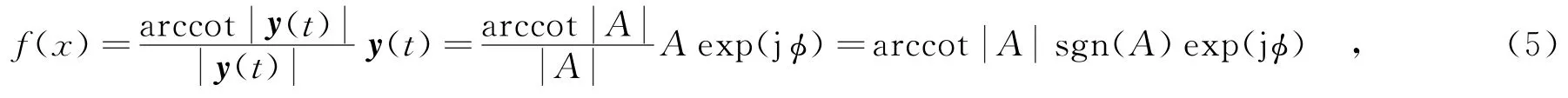
其中,sgn（·)为符号函数.

从式（5)中可以看出,该非线性变换仅将信号的幅值映射到一个有限区间,并未改变信号的相位信息.因此,该非线性变换使Alpha稳定分布噪声下的信号具有二阶及二阶以上统计量,且使瞬时相位谱保持不变.

对于基带信号y（t),其广义四阶累积量表达式为

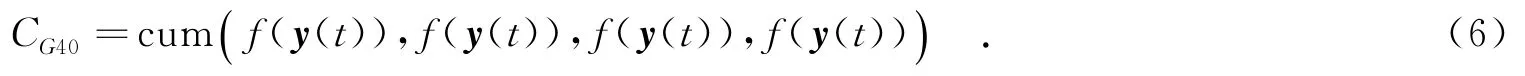
式（3)、式（4)和式（6)中的广义二阶累积量和广义四阶累积量可通过相应矩的采样估计[12]得到.在此假设y（t)是零均值的,则广义二阶累积量和广义四阶累积量的采样估计如下:

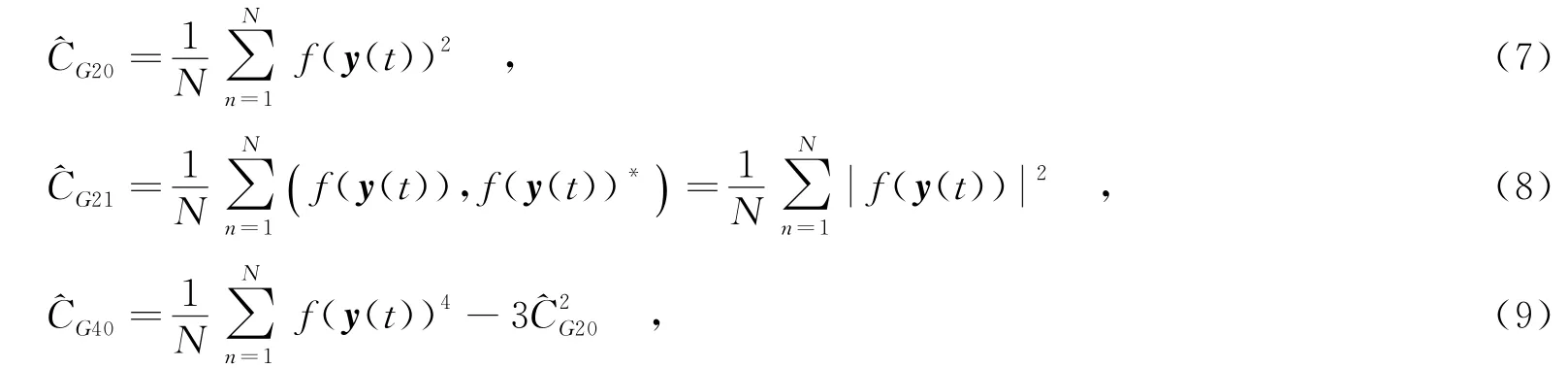
其中,^表示广义累积量的估计.不失一般性,假设星座点已经归一化为单位能量,即CG21=1,则归一化的累积量估计为

忽略噪声的影响,由于双相相移键控（Binary Phase Shift Keying,BPSK),4振幅键控（Amplitude Shift,Keying,ASK)信号的CG20的理论值为1,最小频移键控（Minimum Shift Keying,MSK),QPSK,8相移键控（Phase Shift Keying,PSK)信号的CG20的理论值为0,因此,可以通过特征F1=CG20和最小均方误差准则分类器将信号备择集{BPSK,4ASK,MSK,QPSK,8PSK}分为两类:{BPSK,4ASK}和{MSK,QPSK,8PSK}.由于BPSK信号和4ASK信号CG40的理论值分别为2和1.36,因此,可以通过特征F2=CG40和最小均方误差准则分类器将信号集合{BPSK,4ASK}中BPSK信号和4ASK信号识别出来.由于QPSK信号和8PSK信号CG40的理论值分别为1和0,因此,可以通过特征F2=CG40和最小均方误差准则分类器可将信号集合{QPSK,8PSK}中QPSK信号和8PSK信号识别出来.其中,最小均方误差准则分类器可表示为[8]

2.2 基于分数阶傅里叶变换的零中心归一化广义瞬时相位谱密度的最大值

信号x（t)的分数阶傅里叶变换（FRactional Fourier Transform,FRFT)的定义为[9]

其中,Kθ（t,u)为分数阶傅里叶变换的核函数,其表达式为

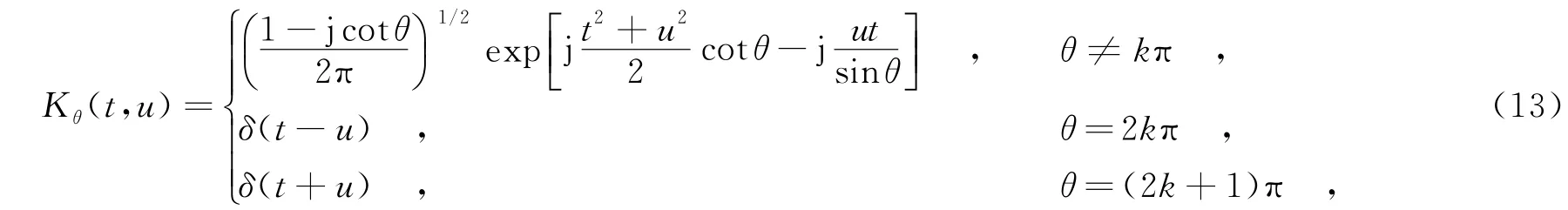
其中,k为整数,Fθ[·]为旋转角度为θ的分数阶傅里叶变换的算子,θ=pπ2,p是分数阶傅里叶变换的阶数,δ（·)为冲激函数.

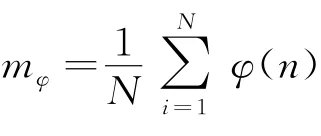
MSK信号的广义瞬时相位φ（n)=2πfcn+πa（m)rbn2,其中rb为码元速率,a（m)∈{0,1}.QPSK信号和8PSK信号的广义瞬时相位φ（n)=2πfcn+φ（m).对于QPSK信号,φ（m)∈{0,π/2,π,3π/2};对于8PSK信号,φ（m)∈{0,π/4,π/2,3π/4,π,5π/4,3π/2,7π/4}.由于信号的码元速率rb比较大,所以MSK信号的广义瞬时相位的变化比QPSK和8PSK信号的大.因此,可以利用信号之间的瞬时相位的变化大小的差异进行MSK信号、QPSK信号和8PSK信号之间的识别.假设MSK信号的特征值在γMSK附近上下波动,QPSK信号的特征值在γQPSK附近上下波动,8PSK信号的特征值在γ8PSK附近上下波动,那么,γMSK＞γQPSK且γMSK＞γ8PSK.根据以上分析,门限δ的设定如下:

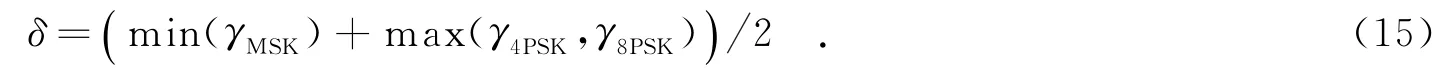
其中,min（γMSK)表示MSK信号的特征值γMSK的最小值,max（γ4PSK,γ8PSK)为QPSK和8PSK信号的特征值γQPSK和γ8PSK的最大值.根据特征参数γmax和门限δ可以将待识别信号集分为两类:{MSK}和{QPSK,8PSK}.

3 仿真结果及性能分析

为了验证文中所提识别方法的有效性,利用MATLAB仿真软件进行仿真实验.实验的仿真条件如下:待识别的信号为BPSK,QPSK,8PSK,4ASK和MSK信号,噪声为Alpha稳定分布噪声,信号的载波频率fc=3.0 k Hz,码元速率rb=1 200 Baud,采样频率fs=19.2 k Hz,采样点数为3 000点,蒙特卡洛仿真次数为500.以正确识别率P来评估算法的性能,其表达式为

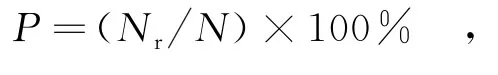
其中,Nr为识别正确的次数,N为总的实验次数.

实验1 测试不同混合信噪比[2]下信号的识别性能.Alpha稳定噪声的特征指数为1.5,成形脉冲的滚降系数为0.35,混合信噪比的变化范围是-10 dB到6 dB.仿真结果如图1所示.从图1中可以看出,信号的正确识别率随着混合信噪比的增大随之提高.当混合信噪比为-2 dB时,信号的正确识别率均为100%.可见,Alpha噪声下文中所提的识别方法在低混合信噪比条件下可以有效地对信号进行识别.

图1 不同混合信噪比下信号的正确识别率

实验2 测试不同的特征指数α对识别性能的影响.特征指数α的变化范围是0.2到2,混合信噪比为0 d B,仿真结果如图2所示.从图2可以看出,当0.4≤α≤2,混合信噪比为0 dB时,BPSK,QPSK,8PSK和MSK信号的正确识别率均大于98%,并且识别性能随着α的增大而逐渐提升.当α≥1时,信号的正确识别率基本不受特征指数的影响;当α=2时,即在高斯噪声下,文中所提的识别方法也可以有效地进行信号的识别.

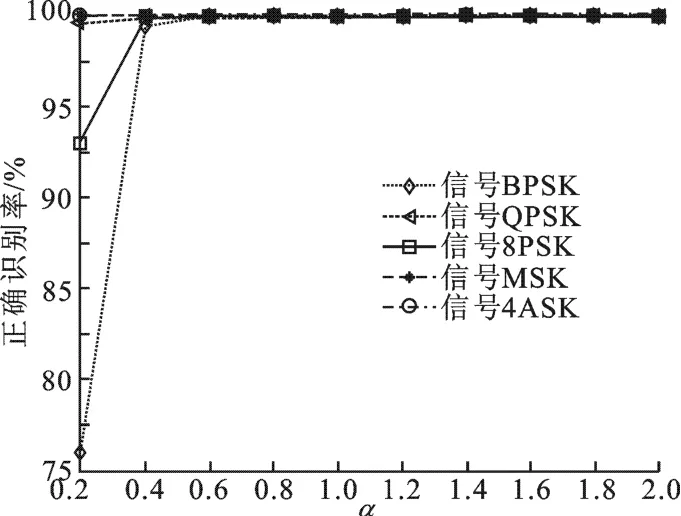
图2 不同特征指数α下信号的正确识别率

实验3 在相同的仿真环境和参数设置下,将文中所提方法的平均识别率与现有文献方法的平均识别率进行实验对比.Alpha稳定噪声的特征指数为1.5,成形脉冲的滚降系数为0.35,混合信噪比的变化范围为-10 d B到6 d B,间隔为2 d B,仿真结果如图3所示.从图3可以看出,相比于现有文献[7-8]的方法,文中方法的识别性能在低混合信噪比条件下均有比较显著的提高.

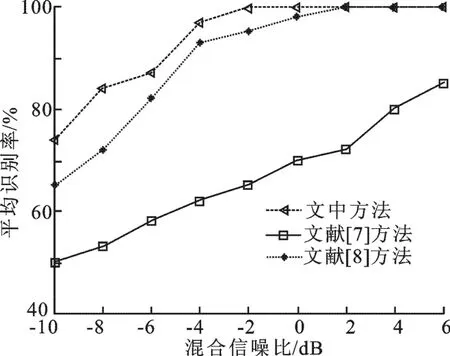
图3 不同方法的识别性能对比

4 结束语

针对Alpha稳定分布噪声下信号的二阶及以上累积量失效的问题,文中构造了基于广义累积量和广义相位的特征.根据广义累积量和广义相位的性质,提出了一种有效识别Alpha稳定噪声下数字调制信号的方法.通过提取信号的分数阶傅里叶变换的零中心归一化广义瞬时相位谱密度的最大值和构造广义累积量的特征参数,实现了5种常用数字调制信号的识别.仿真结果表明,在Alpha稳定噪声下,文中方法的识别性能优于现有的方法.

[1]Ben C W,Dayoub I,Hamouda W,et al.Modulation Recognition for MIMO Relaying Broadcast Channels with Direct Link[J].IEEE Wireless Communications Letters,2014,3(1):50-53.

[2] 李兵兵,马洪帅,刘明骞.Alpha稳定分布噪声下时频重叠信号的载波频率估计方法[J].电子与信息学报,2014,36 (4),868-874. Li Bingbing,Ma Hongshuai,Liu Mingqian.Carrier Frequency Estimation Method of Time-frequency Overlapped Signals with Alpha-stable Noise[J].Journal of Electronics&Information Technology,2014,36(4):868-874.

[3]Jin Y,Ji H B.Robust Symbol Rate Estimation of PSK Signals under the Cyclostationary Framework[J].Circuits System and Signal Processing,2014,33:599-612

[4]Wang F G,Wang X D.Fast and Robust Modulation Classification via Kolmogorov-Smirnov Test[J].IEEE Transactions on Communications,2010,58(8):2324-2332.

[5]杨伟超,赵春晖,成宝芝.Alpha稳定分布噪声下的通信信号识别[J].应用科学学报,2010,28(2):111-114. Yang Weichao,Zhao Chunhui,Cheng Baozhi.Recognition of Communication Signals in Noise with Alpha-stable Distribution[J].Journal of Applied Science,2010,28(2):111-114.

[6] 赵春晖,杨伟超,杜宇.采用分数低阶循环谱相干系数的调制识别[J].应用科学学报,2011,29(6):565-570. Zhao Chunhui,Yang Weichao,Du Yu.Modulation Recognition Using Fractional Low-order Cyclic Spectrum Coherence Coefficient[J].Journal of Applied Science,2011,29(6):565-570.

[7] 刘明骞,李兵兵,曹超凤,等.认知无线电中非高斯噪声下数字调制信号识别方法[J].通信学报,2014,35(1):82-88. Liu Mingqian,Li Bingbing,Cao Chaofeng,et al.Recognition Method of Digital Modulation Signals over Non-gaussian Noise in Cognitive Radio[J].Journal on Communications,2014,35(1):82-88.

[8] 赵春晖,杨伟超,马爽.基于广义二阶循环统计量的通信信号调制识别算法研究[J].通信学报,2011,32(1):144-150. Zhao Chunhui,Yang Weichao,Ma Shuang.Research on Communication Signal Modulation Recognition Based on the Generalized Second-order Cyclic Statistics[J].Journal on Communication,2011,32(1):144-150.

[9] 刘明骞,李兵兵,曹超凤.非高斯噪声下数字调制信号识别方法[J].电子与信息学报,2013,35(1):85-91. Liu Mingqian,Li Bingbing,Cao Chaofeng.Recognition Method of Digital Modulation Signals in Non-gauss Noise[J]. Journal of Electronics&Information Technology,2013,35(1):85-91.

[10]赵春晖,杨伟超.Alpha稳定分布噪声下MPSK信号调制识别算法研究[J].沈阳大学学报,2013,25(1):10-14. Zhao Chunhui,Yang Weichao.Modulation Recognition Algorithm of MPSK Signals in Alpha Stable Distribution Noise [J].Journal of Shenyang University,2013,25(1):10-14.

[11]金艳,姬红兵.基于循环自相关的PSK信号盲参数估计新方法[J].西安电子科技大学学报,2006,33(6):892-895. Jin Yan,Ji Hongbing.A New Cyclic Autocorrelation Based Blind Parameter Estimation Method for PSK Signals[J]. Journal of Xidian University,2006,33(6):892-895.

[12]Swami A,Sadler B M.Hierarchical Digital Modulation Classification Using Cumulants[J].IEEE Transactions on Communications,2000,48(3):416-429.

（编辑:李恩科)

Novel recognition method for digital modulation signals with Alpha stable noise

LIU Mingqian,LI Bingbing,SHI Yayun
(State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China)

The traditional methods for digital modulation signals recognition with Alpha stable distribution noise have the problem of poor performance.In this paper,a novel recognition method for digital modulation signals based on the generalized cumulant and generalized instantaneous phase is proposed to solve this problem.This method extracts the characteristic parameters which are the generalized cumulant and maximum of normalization and center generalized instantaneous phase spectral density based on fractional Fourier transform.And then the minimum mean square error classifier and the threshold are used to achieve modulation recognition of digital modulation signals with Alpha stable distribution noise.Simulation results show that the proposed method has not only better performance but also lower computation complexity than the traditional recognition methods in an Alpha stable distribution noise environment.

modulation recognition;Alpha-stable distribution noise;generalized cumulant;generalized instantaneous phase;minimum mean square error

TN911.7

A

1001-2400（2015)06-0001-05

10.3969/j.issn.1001-2400.2015.06.001

2014-07-04

时间:2015-03-13

国家自然科学基金资助项目（61501348,61271299);国家博士后科学基金资助项目（2014 M562372);国家“863”高技术研究发展计划资助项目（2007AA01Z288);高等学校学科创新引智计划资助项目（B08038)

刘明骞（1982-),男,讲师,博士,E-mail:mqliu@mail.xidian.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.001.html