基于能量释放的深井巷道断面形状优化

马德鹏，杨永杰，曹吉胜，邢鲁义



基于能量释放的深井巷道断面形状优化

马德鹏1，杨永杰1，曹吉胜2，邢鲁义1

(1. 山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛，266590；2. 中南大学地球科学与信息物理学院，湖南长沙，410083)

选取矩形、直墙拱形、梯形、圆形和椭圆形共5种典型断面形状的巷道，基于UDEC程序分析巷道的围岩能量释放特征、应力及塑性区分布规律，并分析水平构造应力对它们的影响。研究结果表明：巷道围岩稳定性受断面形状影响显著，巷道边界线越光滑，能量释放量越低，主应力差不均匀区域及塑性区范围越小；深井巷道的最优断面形状为圆形及椭圆形。针对围岩的不同应力状态选择不同的断面形状，能够有效减少围岩塑性区及主应力差分布不均匀区域的范围，降低巷道的冲击危险性。

能量释放；水平应力；主应力差；断面优化；数值模拟

根据热力学定律，岩石裂隙闭合、弹性变形、裂隙扩展直至破坏的每个应力−应变过程都对应着相应的能量状态，一直与外界进行能量交换(存储、耗散、释放)，保持能量平衡。而巷道失稳往往是其围岩中能量积聚和突然释放的过程，是能量驱动下的一种状态失稳现象。煤岩体变形失稳是能量耗散与释放的综合结果[1−5]，能量耗散使煤岩体产生劣化和能量丧失，能量释放则是煤岩体整体破坏的内在原因。陈卫忠 等[6]以能量为切入点，研究了其在岩石破裂失稳过程中积聚−耗散特征；崔兰等[7]分析了圆形巷道开挖过程中的能量释放特征及应力分布状况。由于巷道失稳是采动围岩内部能量积聚、迁移、释放的过程，因此，进行能量变化特征研究，对揭示巷道失稳的发生过程以及灾害机理意义重大。同时，随着开采深度加大，巷道矿压出现剧烈变化，冲击危险性显著增强，能量积聚释放特征更加明显。对深部高应力巷道围岩控制进行了研究[8−11]，包括理论分析、物理试验、数值模拟及现场试验等，取得了许多进展，但远未成熟，特别是在深部冲击危险性较大的高应力巷道设计中，技术人员大都重点考虑巷道的支护方式及参数[12]，而对巷道的断面形状、水平应力等因素考虑较少，往往导致巷道支护成本提高而效果欠佳。在不多的针对巷道断面优化的研究中，大都从巷道围岩应力及变形角度进行分析，以圆形巷道为例，通过能量角度探索巷道围岩变形破坏规律，对其他断面巷道的研究较少，使得高应力巷道的设计存在一定局限性。基于此，本文作者选取矿井开采设计中常用的5种巷道断面形状即矩形、直墙拱形、梯形、圆形及椭圆形进行卸荷开挖离散元分析，研究巷道在断面形状、断面面积、埋深、水平应力等因素影响下的能量释放规律、围岩应力及塑性区分布特征，以便为深部高应力巷道设计提供参考。

1 数值模拟方案设计

巷道掘进中发生的非线性、不可逆性的物理、力学效应，产生各种形式的能量变化。UDEC软件的能量分析模块能够较好地计算开挖过程中能量释放规律，且运用提供的FISH语言编写程序能够有效地处理计算结果，因此，本文选用UDEC离散元程序进行数值计算。

数值计算中，选取的巷道断面形状有矩形、梯形、直墙拱形、圆形及椭圆形共5种断面形状，如图1所示。数值计算以山东西南部某矿运输巷道为工程背景，采矿巷道埋深1 km，围岩为砂岩，容重为2.5 kN/m3，岩体的弹性模量为7.2 GPa，泊松比为0.28，黏聚力为2.2 MPa，抗拉强度为1.3 MPa，内摩擦角为38°；模型的长×高为20 m×20 m；底部固定，上表面施加载荷，侧面采用应力边界，基于摩尔-库仑破坏准则。数值模拟计算方案设计如表1所示。

(a) 矩形；(b) 梯形；(c) 直墙拱形；(d) 圆形；(e) 椭圆

图1巷道断面形状

Fig. 1 Cross-section shapes of roadway

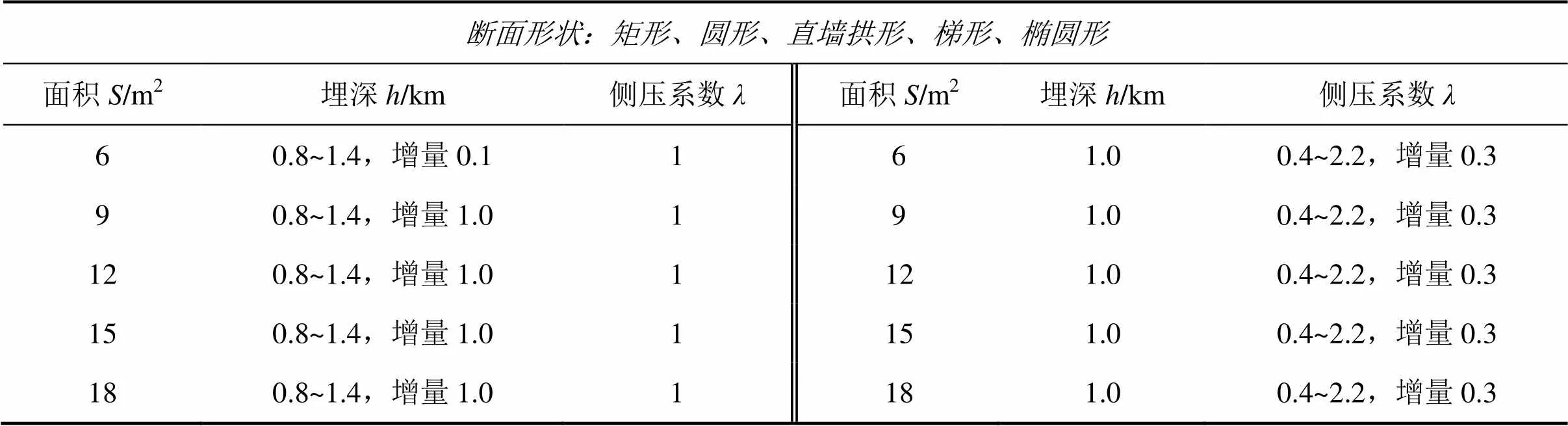
表1 数值模拟方案

2 数值模拟结果分析

2.1 不同埋深及断面面积巷道能量释放特征

在UDEC中导致能量变化的因素有岩石、节理及边界作用等，采用Salamon[13]提出的巷道开挖后围岩能量平衡方程为计算依据，其能量平衡方程为：。式中：r为巷道围岩开挖释放的能量(J)；为系统中的动能(J)；k为质量阻尼耗散能(J)；m为围岩内部储存的应变能(J)；v为围岩变形消耗的能量(J)。同时，为反映任意形状、开挖体积导致的能量释量，引入能量释放率的概念，即=d/d。其中：为能量释放率(J/m3)；d为能量释放量(J)；d为岩体体积(m3))。

对不同埋深(侧压系数=1，断面面积=9 m2)及不同断面面积(=1，埋深=1 km)巷道进行模拟计算，围岩能量释放量及释放率分别如图2和图3所示。

(a) 能量释放量；(b) 能量释放率

1—矩形；2—椭圆形；3—直墙拱形；4—矩形；5—梯形

图2 不同埋深巷道围岩能量释放特征

Fig.2 Energy release characteristics of roadway surrounding rock under different depth

(a) 能量释放量； (b) 能量释放率

1—矩形；2—椭圆形；3—直墙拱形；4—矩形；5—梯形

图3 不同断面面积巷道围岩能量释放特征

Fig. 3 Energy release characteristics of roadway surrounding rock under cross-section area

从图2和图3可见：随着埋深及断面面积的逐渐增大，围岩能量释放量显著增大，当埋深从0.8 km增加到1.4 km的过程中，各断面形状巷道围岩能量释放的增加值均超过4.7 MJ，且埋深越大，每增加0.1 km，围岩能量释放量的增量也越大，从开始的0.597 MJ增加到1.027 MJ；当断面面积从6 m2增加到18 m2时，各断面形状巷道围岩能量释放量增幅在3.5~4.3 MJ之间，其中圆形巷道增幅最小，梯形巷道增幅最大，增长形式均成二次多项式凹形曲线。这表明在深部开采中，随应力水平及断面面积不断增大，巷道开挖能量释放将呈非线性不稳定曲线形式显著增长，发生冲击地压的潜在危害性增大。

同时，随着应力水平的逐渐升高以及巷道围岩应力场分布不均匀程度增大，围岩能量释放率也呈凹形曲线逐渐增大，但其随开挖面积的增大而所降低，如图3所示。

从图3可见：应力水平是决定凹形不稳定曲线增长的关键因素，反映了深部开采巷道失稳比浅部开采巷道的大，这主要是应力水平增加所致。

2.2 不同断面形状巷道应力及能量释放特征分析

为分析断面形状对巷道围岩稳定性的影响，在相同埋深(=1.0 km)、侧压系数(=1.0)、断面面积(=9 m2)的条件下，对5种不同断面形状的巷道进行模拟计算，各断面形状巷道的能量释放量及释放率如图4所示。从图4可知：不同断面形状巷道能量释放量差异性明显，巷道边界线越光滑，能量释放量越低，圆形、椭圆形巷道的能量释放量最小，分别为3.298 MJ和3.359 MJ；拱形的能量释放量次之，为3.591 MJ；矩形、梯形巷道的能量释放量最大，分别为3.842 MJ和3.879 MJ。能量释放量最大与最小值相对误差为17.6%，反映出深部开采中圆形、椭圆形巷道的冲击地压危险性比其他断面形状巷道的小。

1—能量释放量；2—能量释放率

为了进一步分析能量释放特征与巷道围岩应力关系，基于FISH语言编写的程序得到巷道围岩主应力差及塑性区分布特征，如图5所示。巷道掘进使得围岩应力在一定范围内重新分布，从巷道表面围岩移向深部，呈现不均匀分布，由“等效开挖”理论可知，不同断面形状的巷道矿压规律也不完全一致。由图5可知：矩形、梯形巷道主应力差由巷道轴线逐渐向肩角和顶角收缩，呈现出不均匀性，越靠近围岩周边，主应力差分布的不均匀性越显著；距围岩表面距离增大，主应力差分布不均匀程度明显降低。与矩形、梯形巷道相比，直墙圆拱巷道存在曲线边界，主应力差分布不均匀程度较矩形、梯形巷道明显减小；椭圆形、圆形巷道全断面为曲线，巷道周边应力分布均匀，且圆形巷道基本处于均压状态。结合表2可得：矩形、梯形巷道主应力差不均匀区域的范围最大，其次是直墙拱形巷道，椭圆形及圆形巷道的应力差不均匀区域的范围最小。

表2 主应力差及塑性区分布范围

各断面形状巷道围岩塑性区分布相差不大，在高应力作用下，巷道围岩破坏从肩角、底角开始，先在顶底板及两帮形成局部剪切破坏区域，而后剪切破坏区域连接、贯通，产生较大范围的塑性破坏损伤区；围岩以剪切破坏为主，断面形状越光滑，拉伸屈服区域越少。不同断面形状的巷道围压主应力左见图1。

根据表2可得：在高应力作用下，巷道围岩两帮塑性区范围略大于顶底板的塑性区范围；矩形、梯形巷道塑性区域较大，直墙拱形巷道次之，椭圆形、圆形巷道范围最小，且分布较均匀。对比主应力差及塑性区分布图可得：主应力差不均匀区域越大，围岩相应部位的塑性破坏损伤区范围也越大，能量释放量也越高。

(a) 矩形；(b) 梯形；(c) 直墙拱形；(d) 椭圆形；(e) 圆形

通过上述分析可知：圆形、椭圆形为深井巷道断面的最优形状。

2.3 水平应力对巷道围岩稳定性的影响

在矿井深部开采中，巷道除了承受较高的原岩应力外，在构造作用显著地区，水平构造应力起主要作用，使得深部高应力巷道矿压剧烈变化，围岩破坏的程度加大，难以支护[14]。当地质构造作用明显时，地应力对巷道的围岩影响也愈加突出，导致深井高应力巷道围岩的支护效果不理想，长期稳定性降低[15]。

根据不同断面形状的巷道围岩应力、能量释放特征，此处对圆形、椭圆形巷道进行模拟分析，其中椭圆形巷道分2种情况，即长轴分别在水平方向和垂直方向。模拟计算中巷道埋深取1.0 km，断面面积取 9 m2。为研究巷道在不同水平应力作用下围岩应力、塑性区及能量释放特征，侧压系数取0.4，0.7，1.0，1.3，1.6，1.9和2.2共7种情况。

2.3.1 水平应力对巷道围岩能量释放的影响

巷道围岩受不同水平应力作用时，能量释放特征如图6所示。从图6可见：随着侧压系数增大，不同断面形状巷道能量释放量及释放率显著增大；当侧压系数从0.4增加到2.2时，各断面形状巷道围岩能量释放量增幅都在9 MJ以上，呈二次多项式凹形曲线。这表明深部构造应力作用时，随着水平应力不断提高，岩爆发生的概率增大。

1—圆形；2—长轴竖直椭圆形；3—长轴水平椭圆形

不同断面形状的巷道能量释放量及释放率不同，当侧压系数＜1时，随着减少，能量释放量从大至小的巷道分别为长轴水平的椭圆巷道、圆形巷道、长轴垂直的椭圆形巷道；当=1时，水平及垂直方向应力相等，巷道围岩处在均压状态，各个断面形状巷道能量释放量相差很小；当＞1时，随着侧压系数增大，能量释放量从大至小的巷道分别为长轴垂直的椭圆形巷道、圆形巷道和长轴水平的椭圆形巷道。

受深部高应力作用，当＜1时，长轴垂直的椭圆形巷道适应性较好；当=1时，椭圆形及圆形巷道适应性较好；当＞1时，长轴水平的椭圆形巷道适应性较好。

2.3.2 水平应力对巷道围岩应力及塑性区分布的影响

取断面形状分别为圆形、长轴在水平位置及垂直位置的椭圆形巷道进行计算，侧压系数取0.4，0.7，1.0，1.3，1.6，1.9和2.2，巷道断面面积为9 m2，埋深取1.0 km，计算所得的塑性区及主应力差分布状况如表3所示。

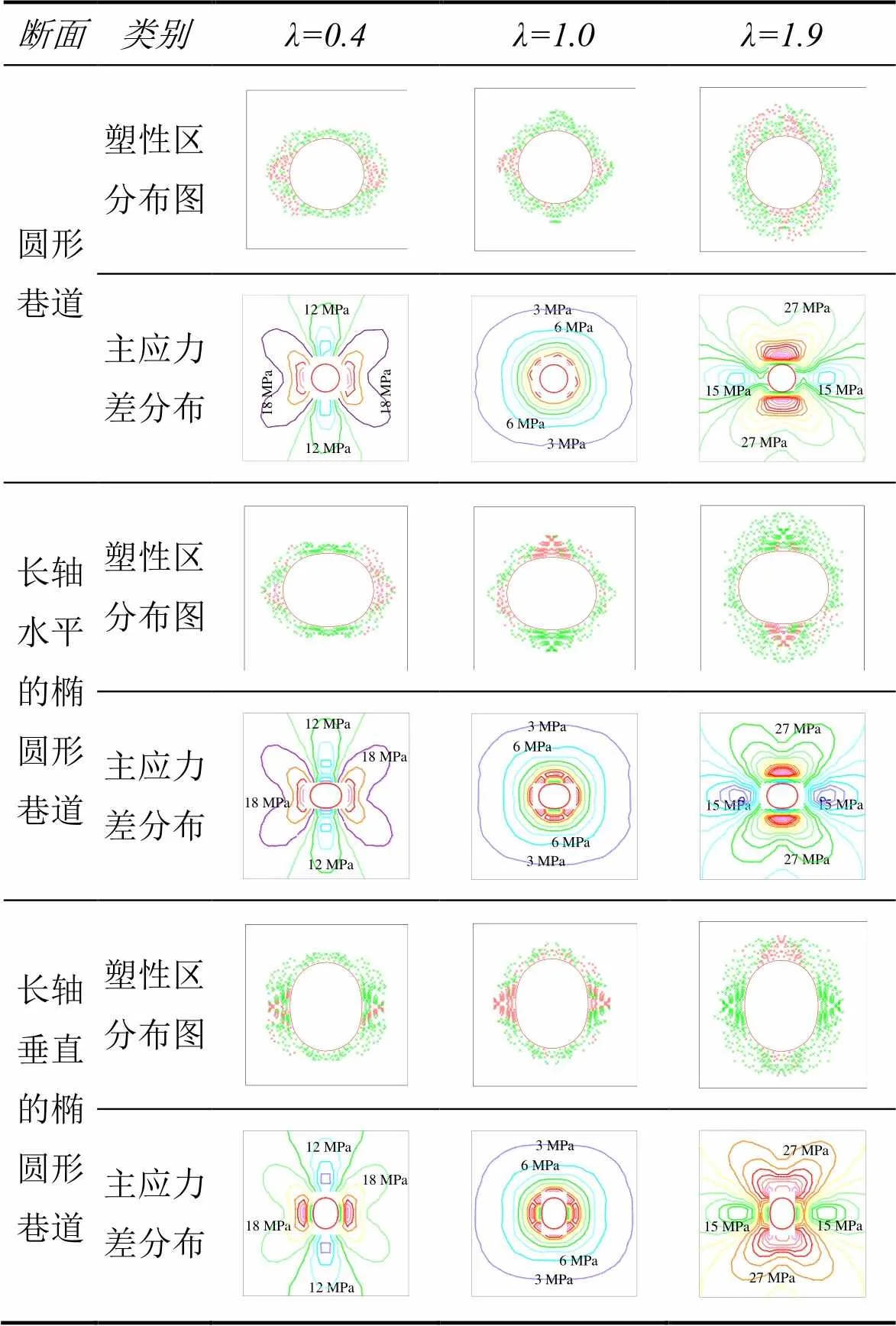
表3 不同侧压系数巷道围岩塑性区与主应力差分布特征

由表3可得：当＜1时，随着侧压系数的减小，塑性区呈“矮胖”型，其分布范围在水平方向上呈递增趋势，垂直方向上则变化不大；巷道围岩两帮及顶底板产生主应力差包核区，主应力差对称出现；长轴在垂直方向椭圆形巷道围岩的主应力差峰值比圆形巷道及长轴在水平方向的椭圆形巷道要小。

随侧压系数减小主应力差呈现递增的趋势，两帮产生的主应力差峰值及范围相对于顶底板来说更大。因此，在低水平应力状态下，巷道两帮为重点监测部位。由于在弹−塑性分布交界区域出现主应力差峰值，这表明随侧压系数减少，塑性区在水平方向上的范围持续加大。

当=1时，巷道围岩处于均压状态，围岩塑性区在巷道四周基本上呈均匀分布，塑性区分布近似圆形。巷道两帮及顶底板主应力差峰值一致。

当＞1时，随侧压系数逐渐增加，塑性区分布范围在垂直方向逐渐增加，在水平方向上则变化较小，但巷道围岩的塑性区域呈明显增加趋势，且塑性区呈瘦高型分布。随侧压系数增大，主应力差也呈现递增的趋势，且巷道顶底板与两巷主应力差也逐步增大，顶底板产生的主应力差峰值及包核区范围相对于两帮来说更大。因此，在高水平应力状态下，巷道顶底板为重点监测部位。

经综合分析，可得水平应力对巷道围岩塑性区和主应力差分布的影响规律为：当水平应力较大时, 巷道围岩主应力差峰值出现在垂直方向，塑性区在垂直方向的发育范围较水平方向的范围大，故需尽量减少垂直方向上的主应力差及塑性区的分布，降低巷道顶底板的变形量，在此情况下，应选用长轴水平的椭圆形巷道；当水平应力较小时，巷道围岩主应力差峰值出现在水平方向，水平方向的塑性区发育范围较垂直方向的大，故需在水平方向上尽量减少主应力差及塑性区分布范围，降低巷道两帮的变形量，此时，长轴在垂直方向的椭圆形为合理的巷道断面形状。

3 结论

1) 随着埋深增加，巷道围岩能量释放量及释放率呈凹形曲线显著增加；随着断面面积增大，能量释放量呈类似特征，但能量释放率逐渐降低。

2) 不同断面形状巷道能量释放量、主应力差及塑性区分布差异性明显；巷道边界线越光滑，能量释放量越低，主应力差不均匀区及塑性破坏区范围也越小；圆形、椭圆形巷道开挖后受力情况最好，冲击危险性要比其他断面形状巷道的小。

3) 当侧压系数＜1时，随着减小，主应力差呈现递增的趋势，两帮产生的主应力差峰值及范围相对于顶底板来说较大；当=1时，巷道两帮及顶底板主应力差峰值基本一致；当＞1时，随着增大，主应力差呈现递增的趋势，顶底板和两帮主应力差也逐步增大，顶底板产生的主应力差峰值及包核区范围比两帮的强。

4) 断面形状及侧压系数对巷道围岩的稳定性产生显著影响，在深部巷道设计中应综合考虑。当水平应力起主导作用时，应选用的断面形状为长轴水平的椭圆形；当垂直应力起主导作用时，应选用长轴垂直的椭圆形。

[1] 何满潮, 苗金丽, 李德建, 等. 深部花岗岩试样岩爆过程实验研究[J]. 岩石力学与工程学报, 2007, 26(5): 865−876. HE Manchao, MIAO Jinli, LI Dejian, et al. Experimental study on rockburst processes of granite specimen at great depth[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 865−876.

[2] Vahid H, Peter K. Brittleness of rock and stability assessment in hard rock tunneling[J]. Tunneling and Underground Space Technology, 2003, 18(1): 35−48.

[3] 曹文卓, 李夕兵, 周子龙, 等. 高应力硬岩开挖扰动的能量耗散规律[J]. 中南大学学报(自然科学版), 2014, 45(8): 2759−2767. CAO Wenzhuo, LI Xibing, ZHOU Zilong, et al. Energy dissipation of high-stress hard rock with excavation disturbance[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2759−2767.

[4] 王耀辉, 陈莉雯, 沈峰. 岩爆破坏过程能量释放的数值模拟[J]. 岩土力学, 2008, 29(3): 790−794. WANG Yaohui, CHEN Liwen, SHEN Feng. Numerical modeling of energy release in rockburst[J]. Rock and Soil Mechanics, 2008, 29(3): 790−794.

[5] 赵毅鑫, 姜耀东, 田素鹏. 冲击地压形成过程中能量耗散特征研究[J]. 煤炭学报, 2010, 35(12): 1979−1983. ZHAO Yixin, JIANG Yaodong, TIAN Supeng, et al. Investigation on the characteristics of energy dissipation in the preparation process of coal bumps[J]. Journal of China Coal Society, 2010, 35(12): 1979−1983.

[6] 陈卫忠, 吕森鹏, 郭小红, 等. 脆性岩石卸围压试验与岩爆机理研究[J]. 岩土工程学报, 2010, 32(6): 963−969. CHEN Weizhong, LÜ Senpeng, GUO Xiaohong. Unloading confining pressure for brittle rock and mechanism of rock burst[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(6): 963−969.

[7] 崔兰, 王树仁. 深部圆巷开挖围岩能量耗散特征数值模拟分析[J]. 山东大学学报(工学版), 2009, 39(4): 102−106. CUI Lan, WANG Shuren. Numerical simulation of the energy dissipation characteristics of an excavated circular tunnel under high stress conditions[J]. Journal of Shandong University (Engineering Science), 2009, 39(4): 102−106.

[8] 柏建彪, 王襄禹, 贾明魁, 等. 深部软岩巷道支护原理及应用[J]. 岩土工程学报, 2008, 30(5): 632−635. BAI Jianbiao, WANG Xiangyu, JIA Mingkui, et al. Theory and application of supporting in deep soft roadways[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 632−635.

[9] 靖洪文, 李元海, 许国安. 深埋巷道围岩稳定性分析与控制技术研究[J]. 岩土力学, 2005, 26(6): 877−888. JING Hongwen, LI Yuanhai, XU Guoan. Analysis of surrounding rock stability of deeply buried roadways and study on its control techniques[J]. Rock and Soil Mechanics, 2005, 26(6): 877−888.

[10] 刘泉声, 张华, 林涛. 煤矿深部岩巷围岩稳定与支护对策[J]. 岩石力学与工程学报, 2005, 23(21): 3732−3737. LIU Quansheng, ZHANG Hua, LIN Tao. Study on stability of deep rock roadways in coal mines and their support measures[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 23(21): 3732−3737.

[11] 常聚才, 谢广祥. 深部岩巷底鼓机理及底板超挖锚注回填技术[J]. 采矿与安全工程学报, 2011, 28(3): 361−369. CHANG Jucai, XIE Guangxiang. Floor heave mechanism and over-excavation & grouting back filling technology in rock roadway of deep mine[J]. Journal of Mining & Safety Engineering, 2011, 28(3): 361−369.

[12] 李海燕, 李为腾, 王德超, 等. 深部厚顶煤巷道纵横钢带联合支护对比研究及机制分析[J]. 中南大学学报(自然科学版), 2013, 44(12): 5075−5083. LI Haiyan, LI Weiteng, WANG Dechao, et al. Comparative study and mechanism analysis of longitudinal-lateral combined steel bands support system in deep roadway with thick top-coal[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 5075−5083.

[13] Salamon. Energy considerations in rock mechanics: Fundamental results[J]. Journal of the South African Institute of Mining and Metallurgy, 1984, 84(8): 233−246.

[14] 孟庆彬, 韩立军, 乔卫国, 等. 深部高应力软岩巷道断面形状优化设计数值模拟研究[J]. 采矿与安全工程学报, 2012, 29(5): 650−656. MENG Qingbin, HAN Lijun, QIAO Weiguo, et al. Numerical simulation of cross-Section shape optimization design of deep soft rock roadway under high stress[J]. Journal of Mining & Safety Engineering, 2012, 29(5): 650−656.

[15] 李桂臣, 张农, 王成, 等. 高地应力巷道断面形状优化数值模拟研究[J]. 中国矿业大学学报, 2010, 39(5): 652−658. LI Guichen, ZHANG Nong, WANG Cheng, et al. Optimizing the section shape of roadways in high stress ground by numerical simulation[J]. Journal of China University of Mining & Technology, 2010, 39(5): 652−658.

(编辑 陈灿华)

Optimization design of cross section shape of deep roadways based on characteristics of energy release

MA Depeng1, YANG Yongjie1, CAO Jisheng2, XING Luyi1

(1. State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology, Shandong University of Science and Technology, Qingdao 266590, China;2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Based on UDEC software and comprehensive analysis of energy release characteristics, the distribution laws of stress and plastic zone of surrounding rock were carried out for five kinds of cross section shapes, i.e. rectangular, trapezoidal, straight-wall-top-arch, circular and oval, and the influence of horizontal tectonic stress was also analyzed. The results show that cross-section shape has great influence on the stability of surrounding rock. When the roadway boundary is smoother, the amount of energy release is lower, and the uneven distribution areas of principal stress differences and the plastic zone are smaller; meanwhile, and the optimal cross section shapes of deep roadway are circular and oval. The reasonable cross section shape chosen according to different stress states of surrounding rock can effectively reduce the range of plastic zone and the uneven distribution areas of principal stress differences as well as the risk of rock burst.

energy release; horizontal stress; principal stress differences; cross-section optimization; numerical simulation

10.11817/j.issn.1672-7207.2015.09.027

TD322

A

1672−7207(2015)09−3354−07

2014−10−12；

2014−12−25

国家自然科学基金资助项目(51379116)；山东科技大学研究生科技创新基金资助项目(YC150302) (Project(51379116) supported by the National Natural Science Foundation of China; Projects(YC150302) supported by the Technology Innovation Foundation of Graduate Student of Shandong University of Science and Technology)

杨永杰，教授，博士生导师，从事岩石力学及矿山压力研究；E-mail: yyj.6125@163.com