基于响应面法的汽车离合器盘毂温锻−冷精整工艺多目标优化
2015-12-21夏玉峰杨建兵田永生杨显红
夏玉峰,杨建兵,田永生,杨显红
基于响应面法的汽车离合器盘毂温锻−冷精整工艺多目标优化
夏玉峰,杨建兵,田永生,杨显红
(重庆大学材料科学与工程学院,重庆,400044)
将温锻−冷精整工艺引入汽车某型离合器盘毂的生产中,结合响应面法(RSM)与弹塑性有限元模拟(FEM)对盘毂冷精整工艺参数的多目标优化问题进行研究。以减小终挤压件轴向翘曲角、减小齿面径向回弹量和降低终挤压件最大损伤值为优化目标,并以精整凸模速度、精整凹模半锥角、温锻件与精整凹模间摩擦因数、精整量以及温锻件法兰厚度为优化变量,采用正交试验设计与Design−Expert V8软件进行RSM拟合建模分析,得到终挤压件的齿面径向回弹量与最大损伤值的二阶响应面模型和终挤压件轴向翘曲角的线性响应面模型,并通过FEM验证模型的准确性,其误差绝对值小于6.3%,可用于后续优化。生产实践表明多目标优化后的温锻−冷精整工艺能够生产出表面质量好、尺寸精确的优良盘毂零件。
离合器盘毂;温锻−冷精整;弹塑性有限元模拟;响应面法;多目标优化
轻型卡车和皮卡车的离合器中广泛使用了盘毂类零件,该类零件由钢颈和异形齿法兰构成,齿形法兰要求具备较高的尺寸精度、形状精度以及良好的表面质量,也是该类零件成形的难点。温(热)冷锻复合成形工艺是从经济与提高材料利用率的角度出发提出的一种近净成形工艺,它结合温(热)锻工艺成形载荷低与冷挤压表面质量好的优点,确保产品具备良好力学性能的同时,尺寸精度与表面质量也达到设计要 求[1−4]。目前国内外常见的关于温(热)冷锻复合成形工艺的报道多是关于成形大模数直齿轮或是一些相关的基础性研究。例如,Stone等[3]研究了把用于板料深拉延件整形的冷熨平技术用于锻件近净成形工艺后处理的可行性,并证明了冷熨平工艺能够在保证零件尺寸精度的前提下有效改善温热锻件的表面质量。Chang等[4]研究了板料深拉延冷精整工艺用于温(热)锻件的重要部位的精整后处理,并以圆柱直齿轮为例验证了冷熨平工艺能够作为一种有效后处理手段实现大模数直齿轮的近净成形。Eyercioglu等[5−6]研究了把精整板料深拉延件的冷熨平技术用于齿轮热锻件的后处理整形。Behrens[1]研究了温(热)锻复合成形工艺加工大模数直齿圆柱齿轮,并且提出了一种新型精整模具结构来补偿终锻件径向回弹和模具变形引起的终挤压件尺寸偏差。朱怀沈等[7]利用弹塑性有限元模拟和广义胡克定律对某型大模数直齿轮温冷锻精整量进行了研究,并确定了某行星轮温锻件的最佳精整量= 0.15 mm。然而,上述关于温(热)冷锻复合成形工艺的研究多是针对某一因素进行的单目标优化方法或是基于某一性能的多目标优化方法,未能考虑不同因素间的耦合关系,这样往往导致提升某一因素水平却引起另一因素水平的下降[8]。因此,本文作者以汽车离合器盘毂为研究对象,针对该类零件温锻−冷精整工艺的一些目标量如终挤压件的轴向翘曲角、径向回弹量和最大损伤值,以精整凸模速度、精整凹模半锥角/2、锻件与精整模具间摩擦因数、整量和锻件法兰高度为优化变量对盘毂温锻−冷精整复合成形工艺进行多目标协同优化研究。采用响应面法作为本文3个目标量的协同优化方法,它能够实现多目标量的合理优化配置,是一种典型多学科设计方法[9],即在本文中实现终挤压件的轴向翘曲角、径向回弹量和最大损伤值3项指标的平衡优化。
1 离合器盘毂温锻−冷精整工艺建立
如图1所示的盘毂零件由异形齿法兰和钢颈构成,是轻卡和皮卡车离合器组件中重要零件之一。图1(a)中齿形上方符号表示齿形回弹性测量位置。零件法兰厚8.0 mm,钢颈高36.5 mm,中心孔直径20 mm,齿顶圆直径53.5 mm,零件材料为AISI−4140 (42CrMo)。零件齿形法兰的形状精度、尺寸精度与齿表面质量均有较高要求。

(a) 盘毂简图;(b) 盘毂三维图
该类零件常规加工方法是采用线切割加工与车削加工,即车削圆棒料获得无齿形法兰,线切割加工成形齿形法兰,其零件成品如图2所示。该方法费时费料,且齿表面质量和力学性能较差,齿形表面要经过磨削才能满足质量要求。

(a) 线切割盘毂正视图;(b) 线切割盘毂侧视图
本文根据该类离合器盘毂的形状特点与工艺要求,结合有限元分析软件DEFORM−3D,提出利用闭塞温挤压成形−冷精整工艺实现该类产品的加工,并围绕盘毂冷精整过程进行多目标优化,其部分成形过程示意图如图3所示。首先加热棒料至始锻温度,采用闭塞挤压模具完成盘毂外轮廓成形,利用冷精整模具(图3(a))精整法兰齿形(图3(b)),最后车削终挤压件获得合格的产品。冷精整过程属于弹塑性变形过程,冷精整量的回弹量可采用广义胡克定律(式(1))与式(2)计算[7]。
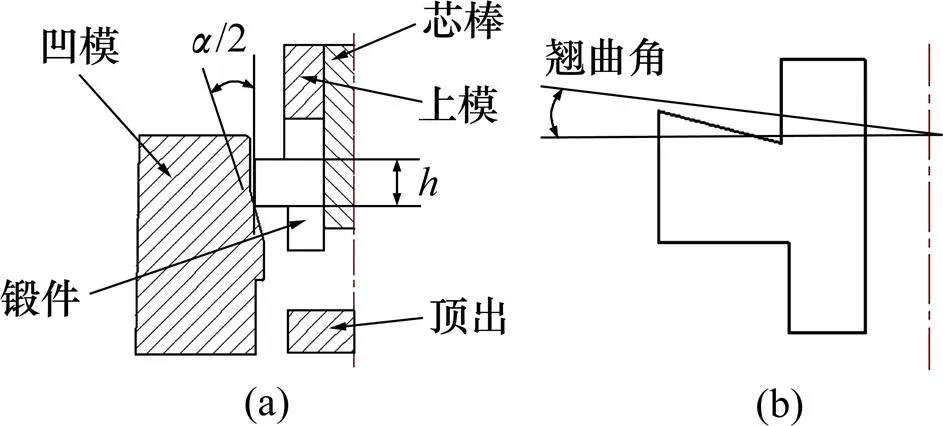
(a) 冷精整模具结构示意图;(b) 轴向翘曲角示意图
本文中=53.5 mm,计算得到盘毂最小精整量min≈0.1 mm。盘毂成品的法兰厚度只有8.0 mm,为了防止精整过程中法兰过度翘曲变形造成最终产品尺寸与形状不合格,有必要在保留机加工余量的情况下适当增加法兰厚度以增强法兰抵抗翘曲变形的能力。因此,综合研究冷精整工艺参数对盘毂终挤压件质量的影响具有重要意义。
本文采用DEFORM−3D弹塑性有限元模型对盘毂冷精整过程进行研究,图4所示为温锻−冷精整方案精整量示意图。盘毂冷精整过程属于弹塑性变形过程,相同精整量下,随着相对壁厚(图4)的减小,齿面径向回弹量会随之减少[10]。因此,测量记录的回弹量为齿顶沿轴向的上端、中部、下端3点中最大值的点,如图1(b)所示。
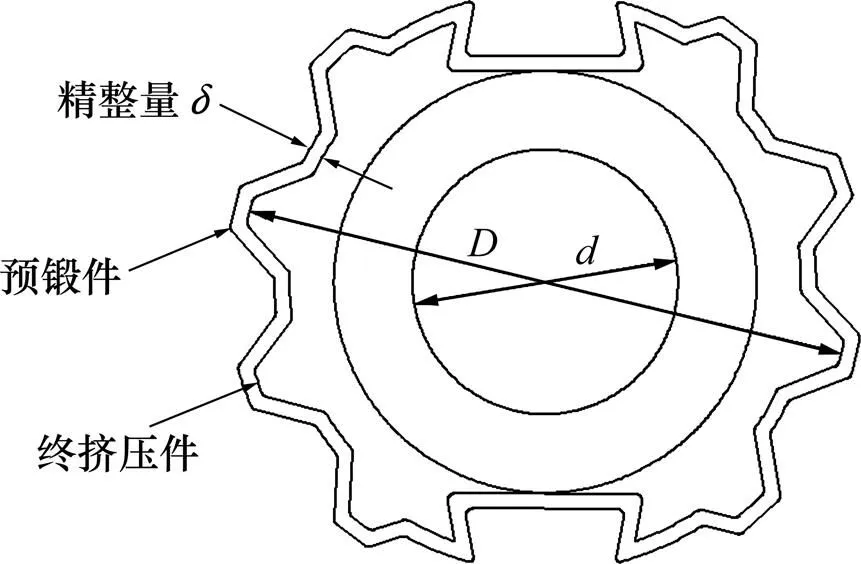
图4 冷精整量示意图
2 数学模型建立
2.1 实验设计及实验结果
使用响应面方法优化分析问题时必须先确定合理的因素以及各因素对应的合理参数水平。精整凹模半锥角/2、精整凸模速度、锻件法兰厚度、精整量、冷精整过程摩擦因数这5个变量分别用1,2,3,4和5表示;回弹量、损伤因子、轴向翘曲角这3个目标量分别以,和表示。
通过正交试验设计检验上述5个变量对目标量影响的显著性,最终选取1,2,3和4作为3个响应目标的优化变量。因此,本文共有4个输入因子,3个响应因子,各输入因子的范围均是根据之前所做的单因素实验确定的。表1所示为各因子水平中心复合设计。此外,实验中摩擦因数均取0.08,精整凹模工作面长度取4 mm。假设所有优化目标的响应模型均为二阶响应面模型,则二阶响应面模型的回归系数共有个。为了获得合理的回归方程,每个变量均取5个水平值(表1),采用中心复合实验设计(CCD)完成实验设计以减少实验次数[11]。借助专业设计软件Design−Expert V8进行实验设计,并借助该软件完成后续响应面分析。利用表1所示的输入因子水平进行4因素5水平CCD,共计30组实验。部分实验方案与实验结果如表2所示。
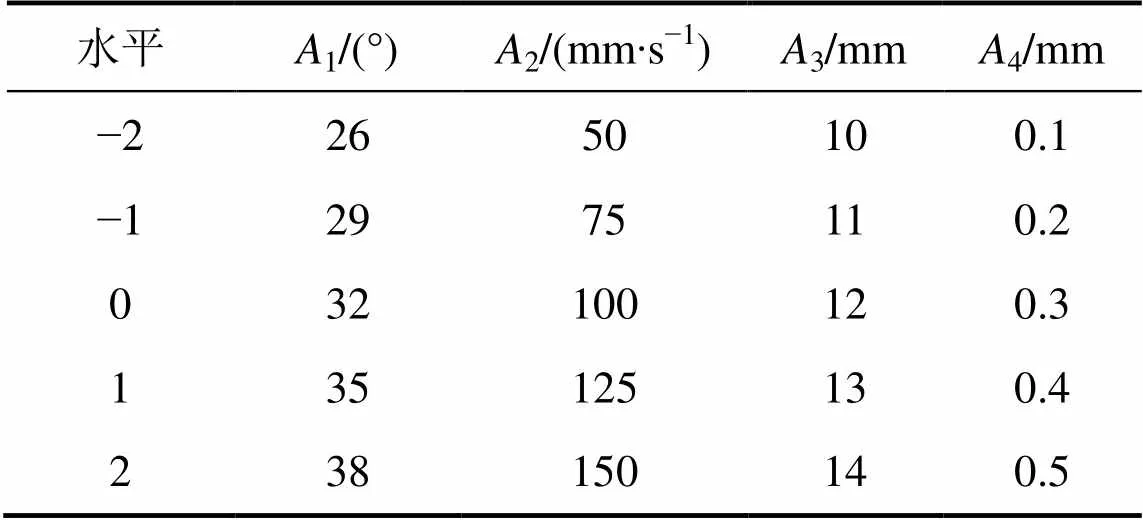
表1 各因子水平中心复合设计
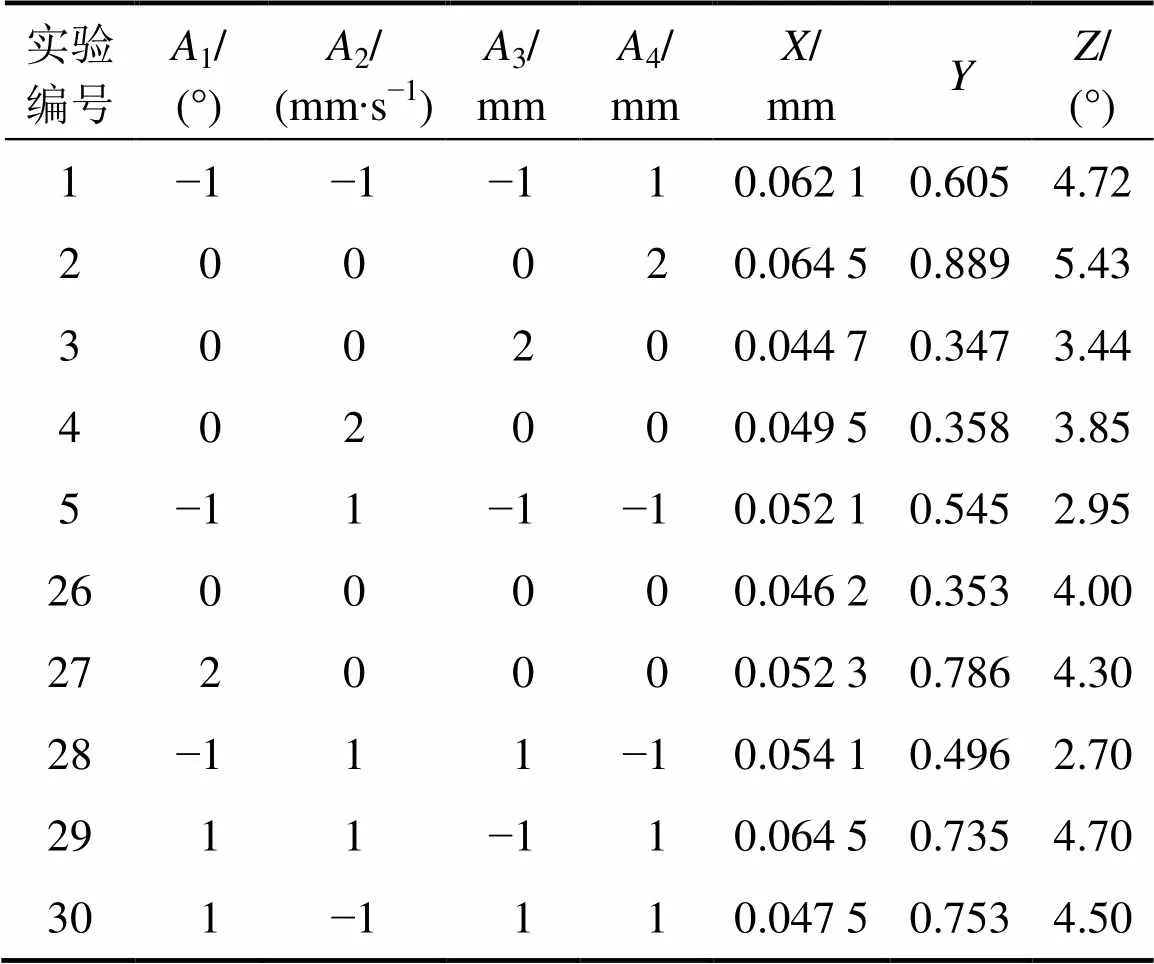
表2 部分实验方案及实验结果
2.2 响应面模型的选择
Design−Expert V8软件实验设计要求尽可能遵守高阶模型设计准则[12]。由方差其次性检验的值()检验响应模型的显著性,为概率,当>的值(>)小于0.05时,即认为该指标是显著的;而>的值(>)小于0.01时,即为高度显著[10]。表3~5所示分别为回弹量、最大损伤值和翘曲角的多种模型方差分析比较结果。表6~8所示分别为回弹量、最大损伤值和翘曲角的2综合分析结果。由表3~5可知:3个模型对应的(>)依次为<0.000 1,<0.000 1和0.000 1,均远小于0.010 0,说明3种模型均是非常显著的。由表6~8可知:目标量回弹量、最大损伤值的最优响应模型均为二次方模型,而目标量翘曲角的最优响应模型为线性模型。

表3 多种模型方差分析比较(回弹量)

表4 多种模型方差分析比较(最大损伤值)
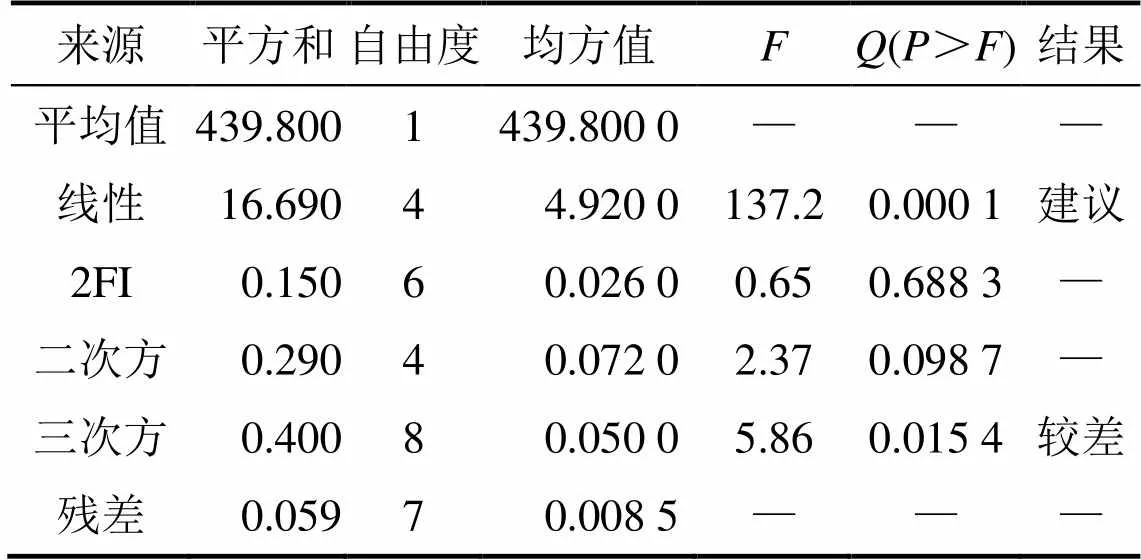
表5 多种模型方差分析比较(翘曲角)
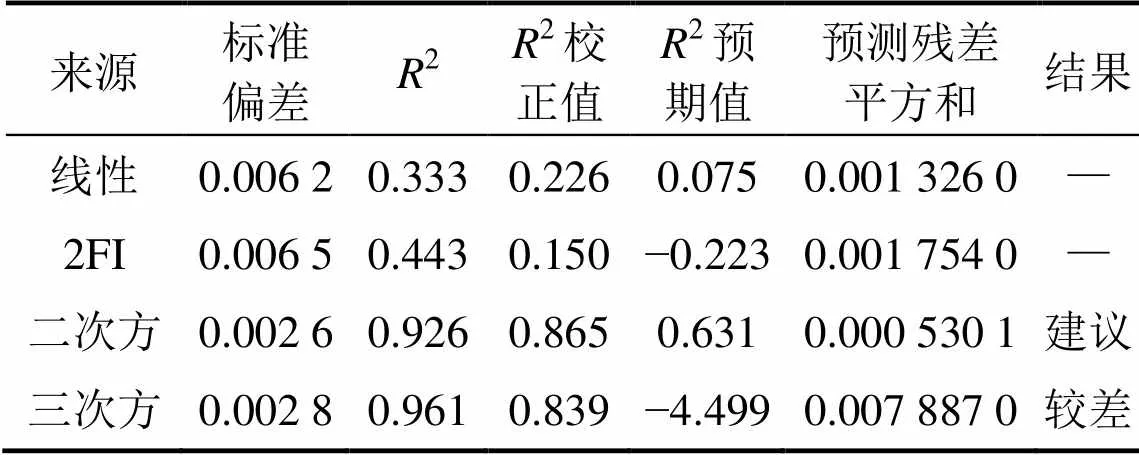
表6 R2综合分析(回弹量)

表7 R2综合分析(最大损伤值)
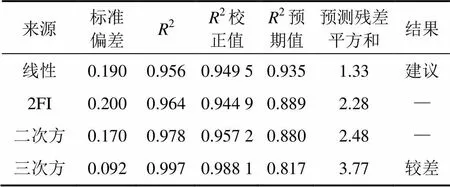
表8 R2综合分析(翘曲角)
此外,还可通过2和adj进一步检验模型的可靠性,一般认为2和adj越大,表明回归模型的拟合程度越好[13]。由表6~8还可知:3个模型的2分别为92.6%,90.2%和95.6%,说明模型具有较高的预测精度。综上所述,3个预测模型能够较好地描述目标量,和关于设计变量1,2,3和4的响应,并能获得较高的预测精度,可用于后续工艺优化。
3 方差分析与数学模型建立
利用方差分析比较不同交互因素作用对响应目标影响的显著性。表9~11所示分别为回弹量、最大损伤值、翘曲角的方差分析结果。由表9~11可知:交互因素对目标响应值影响的显著性如下:对回弹量影响最显著的交互因素是法兰厚度与精整量;对最大损伤值影响最显著的交互因素为入模半锥角与精整量;翘曲角的响应模型为线性模型,各因素中对其影响较大的是精整量与入模半锥角。
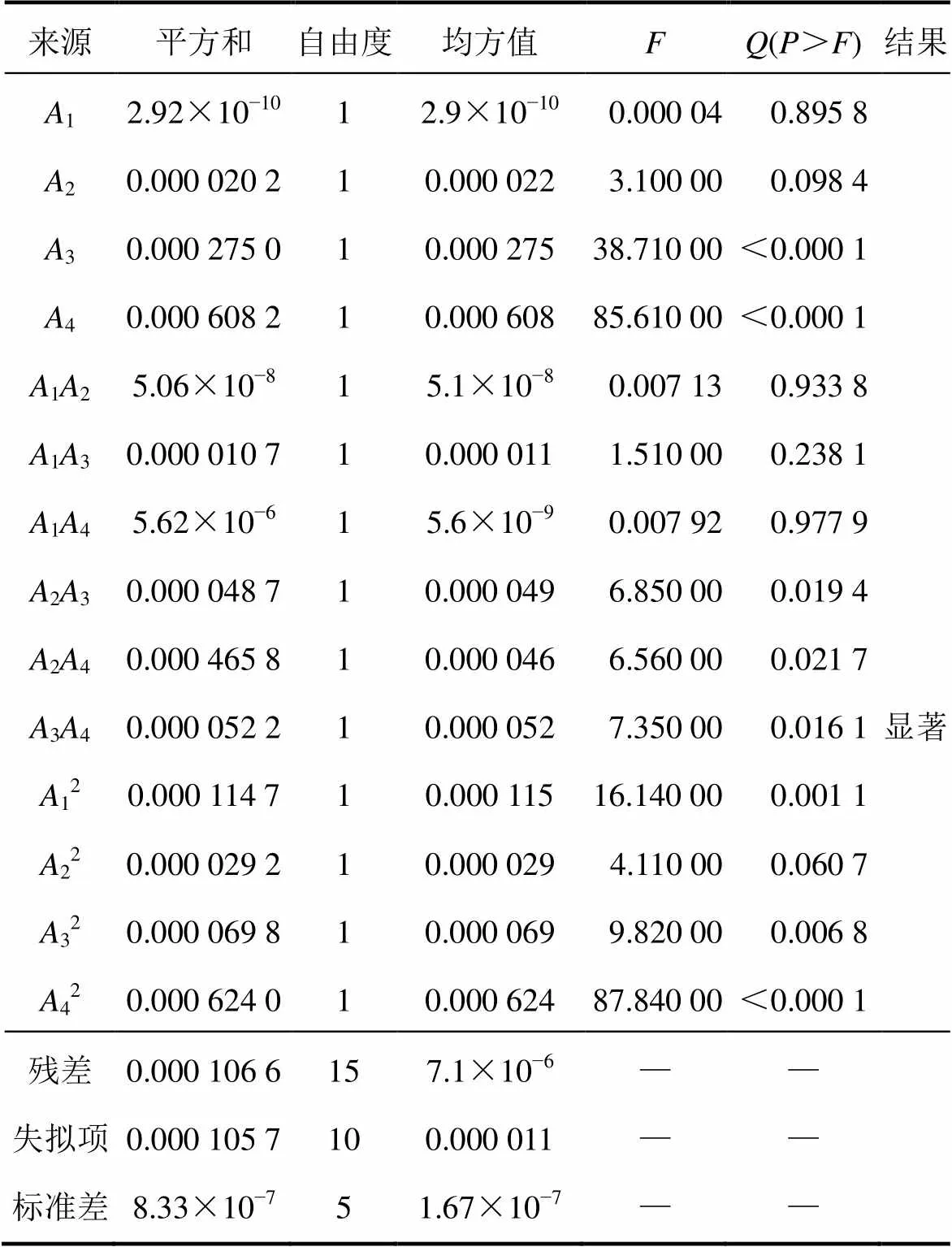
表9 回弹量方差分析

表10 最大损伤值方差分析
表11 翘曲角方差分析
响应因子,和与温锻−冷精整工艺参数的数学模型分别如式(3)~(5)所示,式(3)~(5)均采用因素代码的形式表示。
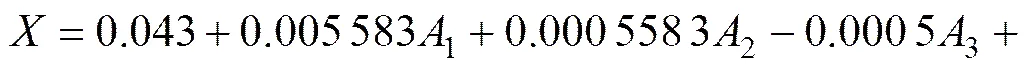


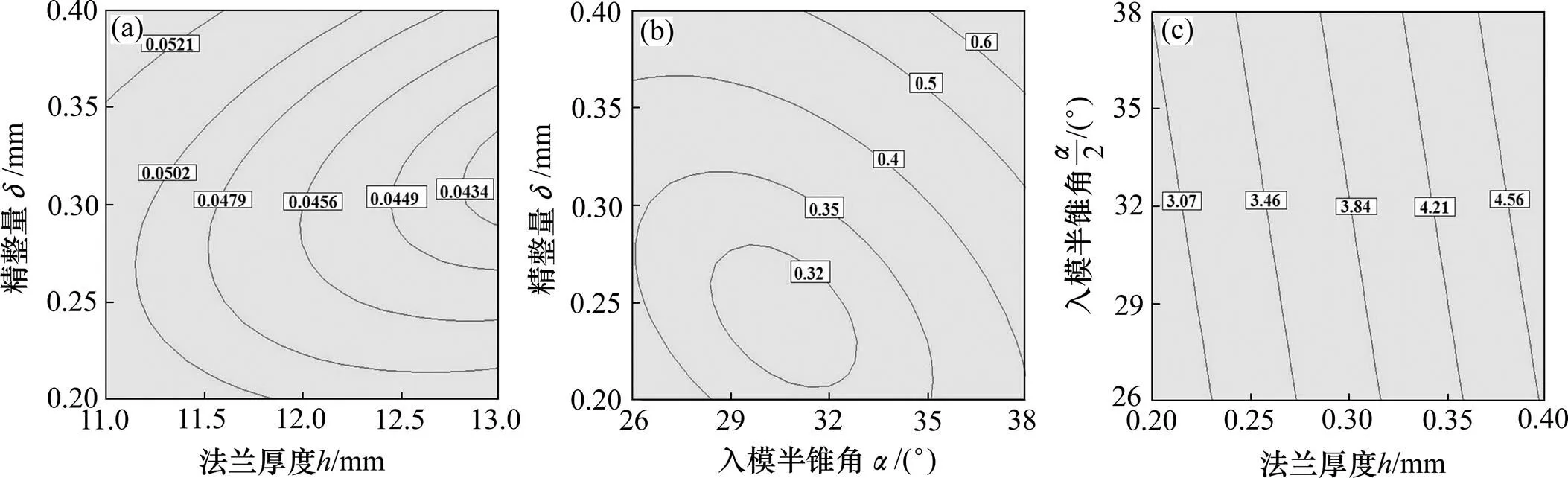
现对各个响应因子影响最显著的交互性因素进行分析。图5所示为入模半锥角为30°与精整凸模速度为100 mm/s时法兰厚度与精整量的等高线图,法兰厚度为13 mm与精整凸模速度为100 mm/s时终挤压件最大损伤值的等高线图和精整凸模速度为100 mm/s与法兰厚度为13 mm时入模半锥角与精整量的等高线图。
从图5(a)可以看出:当入模半锥角为30°且精整凸模速度为100 mm/s时,响应值回弹量随着精整量的增加而逐渐减小;当精整量大于0.3 mm时,回弹量又随着精整量的增加而略微增加。同时回弹量随着法兰厚度的增加而减小,这是由于增加法兰厚度增强了法兰抵抗翘曲变形的能力,减小了精整时法兰整体翘曲变形量,使整形部分塑性变形量增加,径向弹性变形量减小,回弹量降低。当法兰厚度为13 mm且精整量约为0.3 mm时,回弹量小于0.043 4 mm。
(a) 回弹量;(b) 最大损伤值;(c) 轴向翘曲角
从图5(b)可知:当法兰厚度取13 mm且精整凸模速度为100 mm/s时,响应值最大损伤值随着精整量的增加出现略微下降;当精整量大于0.25 mm时,最大损伤值随着精整量的增加而增加。同时当入模半锥角较小时,金属流动过程较长容易造成损伤,随着入模半锥角的增加流动距离减小损伤值降低;当入模半锥角继续增加时最大损伤值又随之增加,因为增加入模半锥角会使材料变形时等效应变增加,当入模半锥角过大时可能引起材料发生应力集中,引起精整表面尤其是燕尾槽尖角处发生开裂损伤[14]。当入模半锥约为30°而精整量在0.25 mm左右时最大损伤值低于0.32,该值低于材料损伤阀值。材料损伤阀值一般取0.5~0.7[15]。
从图5(c)可以看出:精整凸模速度为100 mm/s且法兰厚度为13 mm时,响应值翘曲角与入模半锥角和精整量呈线性关系,即轴向翘曲角随着入模半锥角和精整量的增加而增加。二者任一因素水平的增加都会加剧零件的轴向变形,而精整量对轴向翘曲角的影响明显大于入模半锥角对轴向翘曲角的影响。
基于上述关于响应因子对目标函数的影响规律进行数值模拟,法兰厚度取13 mm,入模半锥角取30°,精整凸模速度100 mm/s。当精整量约为0.25 mm时精整效果相对最好,此时终挤压件的径向回弹量低于0.045 mm,最大损伤值低于0.35;当精整量超过 0.5 mm时,齿形上端翘曲变形严重,齿面尤其是燕尾槽尖角处最大损伤值超过材料损伤阀值(0.5~0.7)。因此,在保证最大损伤值和回弹值最小化的同时要确保取得尽量小的轴向翘曲角。
4 实验方案优化与验证
在上述实验分析与模型拟合的基础上利用Design−Expert V8软件对试验参数进一步优化[12],即保证精整轴向翘曲角在一个合理范围内时终挤压件的最大损伤值与径向回弹量达到最小化。表12所示为终挤压件轴向翘曲角小于4.50°、最大损伤值小于0.35以及径向回弹值小于0.045 0 mm的基础上获取的优化方案。
表12中的模型计算值是通过响应面法优化得到的响应值,模拟值是对应工艺参数下,根据有限元模拟得到的响应值。相对误差计算公式如式(6)所示[12]:
式中:为相对误差;1为方案模拟值;2为采用响应模型得到的计算值。
从表12可知:4组优化方案中各个响应值的最大相对误差绝对值小于6.3%,说明通过响应面法优化得到的工艺方案可信度较高。此外,从表12可以看出:方案2的各个响应值的相对误差绝对值均小于5%,说明该方案稳定性好,因此把方案2作为最优工艺参数并用于生产实践。图6所示为采用优化方案2生产的盘毂各阶段产品(图6(a),6(b)和6(c))与盘毂燕尾槽尖角和齿表面的局部放大图(图6(d))。优化后的温锻−冷精整工艺生产的盘毂零件齿表面质量好,尤其是精整时容易产生开裂的燕尾槽尖角处未检出裂纹损伤。利用三坐标仪测量车削后零件精整部位的尺寸,并与方案2的模拟结果进行对比。具体结果如表13所示。
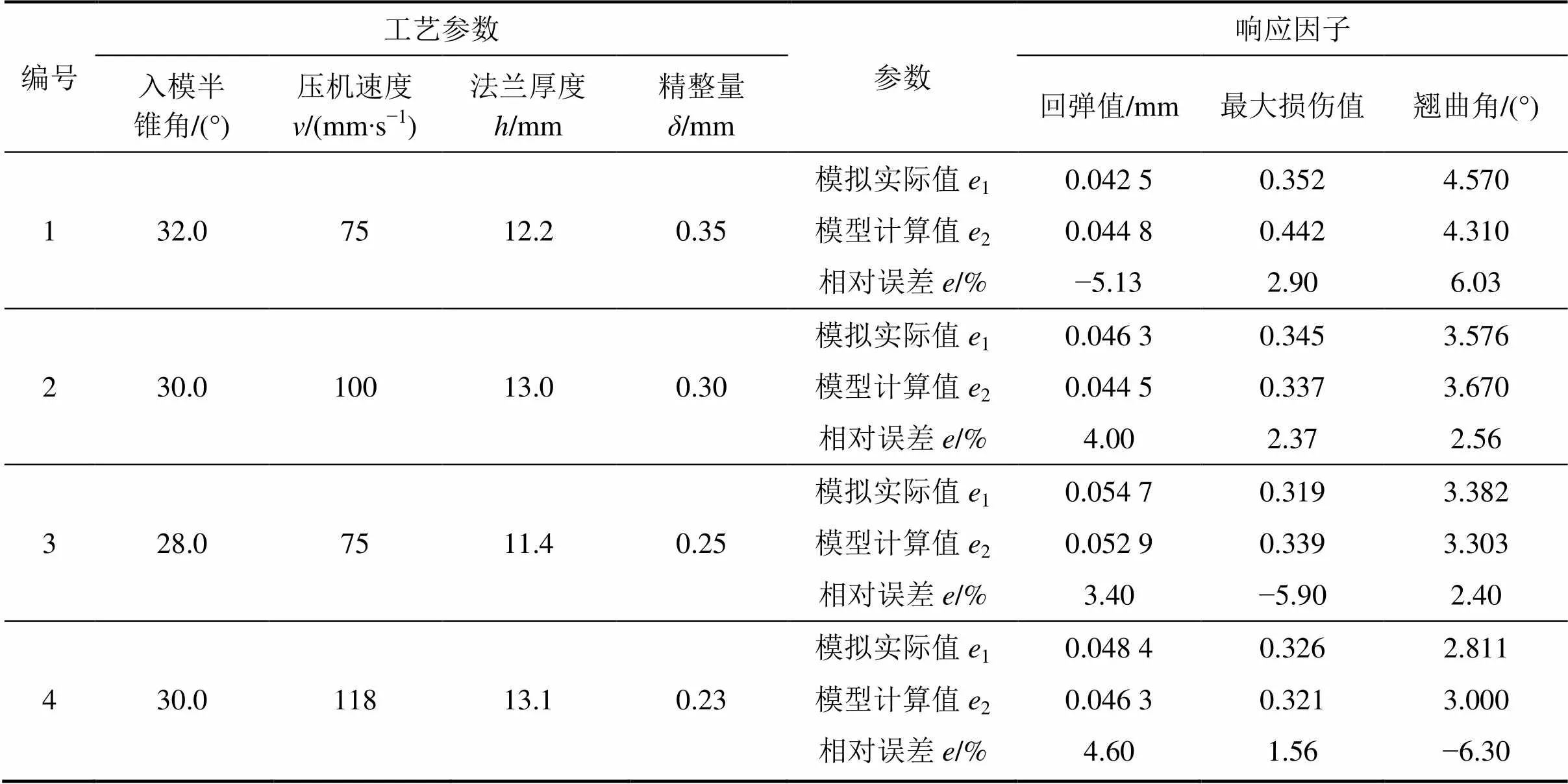
表12 优化工艺参数与结果分析

(a) 盘毂温锻件;(b) 盘毂冷精整件;(c) 机械加工后的盘毂;(d) 盘毂法兰齿形表面质量
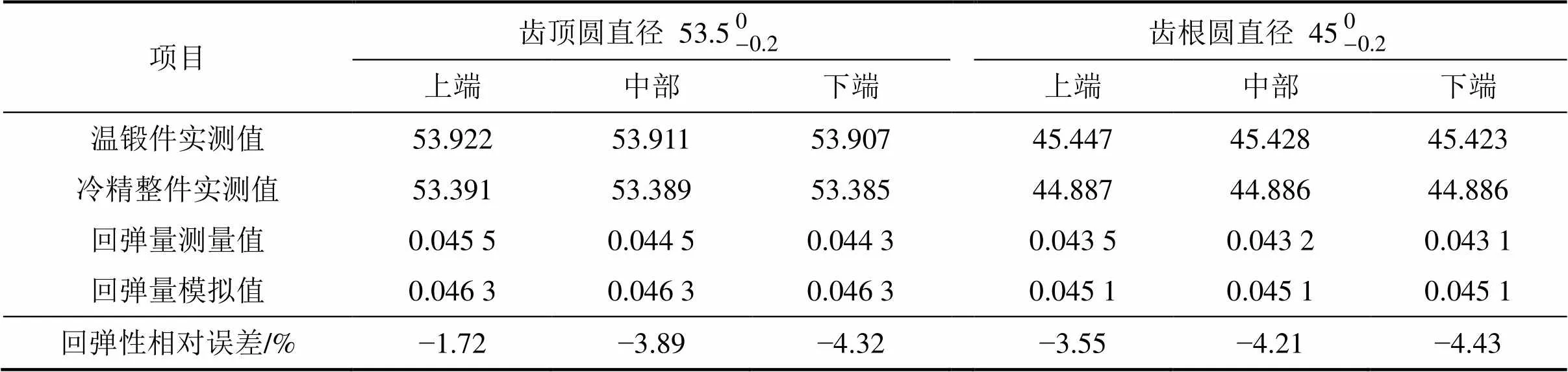
表13 冷精整零件齿顶圆与齿根圆直径与模拟结果对比
表13所示为盘毂2个主体尺寸回弹模拟值与实测值以及二者间的偏差。从表13可以看出:回弹量模拟结果与实测值的相对误差绝对值小于5%,说明响应面法优化的工艺参数合理。试验用冷精整凹模采用组合模具结构,模芯材料用硬质合金YG8,应力圈材料40Cr并做调制处理,冷精整过程最大成形载荷约为 23 t,采用硬质合金的精整凹模使用寿命超过8 000件。此外,优化后的温锻−冷精整工艺生产的离合器盘毂原材料利用率高,与线切割加工原材料利用率相比,提高了约45%,生产效率成倍数增加。综上所述,温锻−冷精整工艺生产出的零件能够很好地满足设计和使用要求,有效保证了法兰齿的表面质量、尺寸精度和形状精度,并可为其他同类产品的生产提供指导。
5 结论
1) 将温锻−冷精整成形工艺引入某类带有齿形法兰的汽车离合器盘毂的生产中,并借助响应面法对新工艺进行了多目标优化设计。
2) 采用Design−Expert V8软件和弹塑性有限元分析对新工艺进行了实验设计、结果分析及优化,获得了目标量的多目标优化数学预测模型。
3)通过误差优化分析与生产验证,新型成形工艺能够生产出表面质量好、尺寸精度和形状精度高的盘毂零件。
4)新工艺生产效率高,模具使用寿命大大增加,与线切割生产工艺材料利用率相比,新工艺原材料利用率提高了约45%,经济效益显著,同时也可为其他同类产品的生产提供指导作用。
[1] Behrens B A. Cold sizing of cold- and hot-formed gears[J]. Manufacturing Technology, 2004, 53(1): 239−242.
[2] 吴诗淳. 冷温挤压技术[M]. 北京: 国防工业出版社, 1995: 58−62. WU Shichun. Cold extrusion technology[M]. Beijing: National Defence Industry Press, 1995: 58−62.
[3] Stone E R H, Cai J, Hu Z M, et al. An exercise in cold ironing as the post-forging operation for net-shape manufacture[J]. Journal of Materials Processing Technology, 2003, 135(2): 278−283.
[4] Chang Y C, Hu Z M, Kang B S, et al. A study of cold ironing as a post-process for net-shape manufacture[J]. International Journal of Machine Tools & Manufacture, 2002, 42(8): 945−952.
[5] Eyercioglu O. Developments and performance analyses of precision forged spur gears[D]. Birmingham: University of Birmingham. College of Material Science and Technology, 1995: 25−36.
[6] Dean T A. The net-shape forming of gears[J]. Materials and Design, 2000, 21(4): 271−278.
[7] 朱怀沈, 夏巨谌, 金俊松, 等. 大模数直齿轮温冷锻精整量的优化选择[J]. 塑性工程学报, 2011, 18(1): 53−57. ZHU Huaishen, XIA Juzhan, JIN Junsong, et al. Optimization of sizing amount during warm-cold compound forging for spur gear with big modulus[J]. Journal of Plasticity Engineering, 2011, 18(1): 53−57.
[8] 刘士士, 谷正气, 伍文广, 等. 基于响应面法的车辆多目标协同优化[J]. 中南大学学报(自然科学版), 2012, 43(7): 2586−2592. LIU Shishi, GU Zhengqi, WU Wenguang, et al. Multi-objective collaborative optimization of vehicle based on response surface methodology[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2587−2592.
[9] ZHAO Weitao, QIU Zhiping. An efficient response surface method and its application to structural reliability and reliability-based optimization[J]. Finite Elements in Analysis and Design, 2013, 67(5): 34−39.
[10] 李倩. 大模数高厚度直齿轮精密成型工艺数值模拟及实验研究[D]. 北京: 机械科学研究总院北京机电研究所, 2011: 35−43. LI Qian. Numerical simulation and experimental research on precise forging process for large module and high thickness spur gear[D]. Beijing: China Academy of Machinery Science & Technology. Beijing Research Institute of Electrical Technology, 2011: 35−43.
[11] Mohamed M N, Amgad A A, Hamdanis, et al. Optimization of reaction parameters of radiation induced grafting of 1-vinylimidazole poly(ethylene-co-tetraflouroethene) using response surface method[J]. Radiation Physics and Chemistry, 2011, 47(16): 52−60.
[12] 刘佳, 张宏, 石岩. 基于Design-Expert V7设计的不锈钢激光非熔透搭接焊工艺优化研[J]. 机械工程学报, 2011, 47(16): 52−60. LIU Jia, ZHANG Hong, SHI Yan. Technology optimization research of laser nonpenetration lap welding of stainless steel based on design-expert V7[J]. Journal of Mechanical Engineering, 2011, 47(16): 52−60.
[13] 彭康, 李夕兵, 彭述全, 等. 基于响应面法的海下框架式采矿结构优化选择[J]. 中南大学学报(自然科学版), 2011, 42(8): 2419−2422. PENG Kang, LI Xibing, PENG Shuquan, et al. Optimization of frame stope structure parameters based on response surface method in under-sea mining[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2419−2422.
[14] 徐波. 大模数花键齿冷挤压成形的研究[D]. 南京: 东南大学材料科学与工程学院, 2006: 39−42. XU Bo. Research on big modulus spline cold extrusion process[D]. Nanjing: Southeast University. College of Materials Science and Engineering, 2006: 39−42.
[15] 夏瑞春. 变速器齿轮轴精密锻造工艺设计[D]. 上海: 上海交通大学机械与动力工程学院, 2008: 47−48. XIA Ruichun. Precision forging process design of transmission gear-shaft[D]. Shanghai: Shanghai Jiao Tong University. School of Mechanical Engineering, 2008: 47−48.
(编辑 罗金花)
Multi-object optimization of warm forging-cold sizing technology for automobile clutch disc-hub based on response surface model
XIA Yufeng, YANG Jianbing, TIAN Yongsheng, YANG Xianhong
(College of Material Science and Engineering, Chongqing University, Chongqing 400044, China)
Warm forging-cold sizing technology was introduced to manufacture a certain clutch disc-hub for automobile. A study on multi-object optimization for clutch disc-hub warm forging-cold sizing technological parameters was conducted by means of response surface methodology and elastic-plastic finite element simulation (FEM). The reduction of final parts’ axial warp angle, the minimizing of tooth surface rebound amount and the decrease of the maximum damage factor were taken as the targets. The cold sizing punch velocity, the half-angle of sizing concave, the friction coefficient between warm forging part and sizing lower die, and the sizing amount of flange were regarded as the optimization variables. Using orthogonal design method and Design−Expert V8 software to analyze the response surface model (RSM), and two quadratic response surface models, a linear response surface model and the optimal value were obtained. A verifying experiment was carried out through elastic-plastic finite element simulation, and the absolute error value of the models was less than 6.3%, which indicates that the models were prominent. At last, production practice results show that the new technology optimized through multi-object optimization could produce qualified clutch disc-hub.
clutch disc-hub; warm forging-cold sizing; elastic-plastic finite element simulation (FEM); response surface model (RSM); multi-object optimization
10.11817/j.issn.1672-7207.2015.09.006
TG316
A
1672−7207(2015)09−3203−08
2014−12−20;
2015−02−20
中央高校基本科研业务费专项资金资助项目(CDJZR13130082) (Project(CDJZR13130082) supported by the Fundamental Research Funds for the Central Universities)
夏玉峰,博士,副教授,从事金属塑性成形技术研究及仿真模拟研究;E-mail: xyfeng@cqu.edu.cn
