地铁隧道爆破开挖引起地表位移沉降的数值模拟

何忠明，蔡军，王利军，罗欣，卫晓波



地铁隧道爆破开挖引起地表位移沉降的数值模拟

何忠明1,2，蔡军2，王利军3，罗欣3，卫晓波3

(1. 长沙理工大学特殊环境道路工程湖南省重点实验室，湖南长沙，410114；2. 长沙理工大学交通运输工程学院，湖南长沙，410114；3. 广州市地下铁道总公司建设总部，广东广州，510380)

以珠江三角洲城际快速轨道交通广州至佛山段工程隧道为依托工程，针对地表受到隧道开挖及爆破的影响引起的沉降问题，运用有限差分软件FLAC3D建立隧道开挖的数值模型，模拟隧道在爆破荷载作用下引起的地表沉降并分析其沉降规律。研究结果表明：在隧道单线洞壁施加爆破荷载后，隧道掌子面和一定范围内的开挖区地表位移沉降对隧道爆破开挖的响应较大，其地表沉降最大值为21.48 mm；在单线隧道爆破开挖引起地表沉降稳定后，进行第2条线隧道爆破开挖时，随着隧道已开挖区至隧道掌子面的距离增大，隧道地表最大位移沉降位置由两线隧道中心向两线隧道地表转变，沉降幅度与到隧道掌子面的距离有关；距隧道开挖掌子面越近，沉降量越大，最大沉降为32.99 mm。

隧道；爆破开挖；地表沉降；冲击荷载

建设地铁不仅能释放城市地面空间、优化交通结构、美化城市环境，而且对市民的出行交通带来便利。然而，在城市隧道建设过程中势必会对隧道地表的土层造成一定的扰动，使土基发生变形。建筑物直接与地表土层相连，所以，施工过程会对土层产生扰动引起土基变形，会使地表建筑物产生不均匀沉降、沉陷、倾斜、开裂等危害[1−3]，对人们的日常生活带来很大影响，故在进行爆破开挖施工时，严格控制地层变形是城市隧道建设施工过程首要考虑的问题。地铁建设是一个极其复杂的施工工程，在施工之前需要研讨相关施工方案。然而，隧道周围的土体是极其复杂的，以至于在施工过程中会引发各种工程问题，并且施工过程带来的地表位移沉降对周围的环境、建筑物的影响难以估计，所以，在地铁隧道爆破施工前，应通过数值模拟等相关手段[4−5]，计算分析地铁隧道爆破施工对地表位移沉降的影响。有关学者对地铁隧道爆破震动效应进行了研究[6−7]，但大多数集中于研究隧道爆破施工过程中地表质点振动速度[8−9]以及盾构施工开挖法开挖隧道引起的地表位移沉降的规律[10−12]，而对地铁隧道爆破开挖引起的地表位移沉降规律的数值研究较少。为此，本文作者通过珠江三角洲城际快速轨道交通广州至佛山段工程的实际地质情况，利用FLAC3D软件建立数值计算模型，对隧道爆破施工过程进行数值模拟，分析隧道爆破施工时隧道上方地表位移沉降规律，以便为工程实践提供参考。

1 计算模型的建立

1.1 工程地质概况

在珠江三角洲城际快速轨道交通广州至佛山段工程沙园站至燕岗站区间，采用矿山法施工。该区间段左线起止里程为ZDK24+728.176~ZDK25+504.591；右线起止里程为YDK24+728.176~YDK25+505.630。路面距隧道拱顶约23 m，隧道的宽高均为6 m，双向，左右两线隧道间距为18 ｍ。隧道下穿昌岗路立交桥、鹤洞大桥桩基、广州供电局河南变电站、居民建筑物等。隧道基岩为泥(砂) 质粉砂岩中风化层，隧道底板位于泥质粉砂岩微风化层，从地面至隧道顶端的地层情况分别是第四系全新人工填筑的杂填土、冲洪积层—粉质黏土、硬塑状残积层—粉质黏土、岩石强风化层。隧道岩土体的物理力学参数根据试验和已有资料进行确定，如表1所示。

表1 岩土体物理力学参数

1.2 数值模型

根据弹性力学中的圣维南原理，数值计算模型的长度取隧道洞跨的8倍，模型的垂直方向从隧道底端至模型底部取洞跨的4倍。结合圣维南原理以及实际工程地质情况，利用FLAC3D软件建立长×宽×高为120 m×50 m×60 m的数值计算模型，并划分网格。划分网格后的计算模型如图1所示。

图1 计算模型

整个数值模拟计算过程分为静力分析和动力分析2部分。静力分析时，前、后、左、右边界条件设置为水平约束；模型的底部设置为固定端约束；模型的上表面为地表，设为自由边界，计算收敛准则为不平衡力比率小于等于10−5。进行动力分析时，去除静力分析模型前、后、左、右、底部5个边界的原有静力边界条件并且施加黏性边界和自由场边界条件，动力计算时间主要依据动力荷载时间来确定。

1.3 模拟隧道开挖过程

采用FLAC3D软件模拟隧道爆破开挖施工。在施工过程中，采用分台阶开挖掘进的方式进行隧道开挖，台阶开挖的长度为5 m(小于隧道的跨度)，采用FLAC3D软件监测隧道整个断面开挖形成之后的地表监测点累计沉降位移。模拟隧道爆破开挖监测地表位移沉降总共分2个工况进行：工况1，隧道未进行开挖时，在重力荷载作用下形成初始应力场，对隧道左线(右线)进行爆破开挖；工况2，左线(右线)爆破开挖之后再进行隧道右线(左线)开挖，分析计算隧道地表在不同工况下的沉降规律。

2 数值模拟方案确定及监测点布设

2.1 爆破震动荷载的输入

为了能较准确地模拟隧道爆破施工时隧道孔壁的冲击荷载，采用段宝福[13]提出的爆破荷载作用时间以及美国高速公路研究所提出的爆破冲击荷载的经验公式所得荷载[14]分别作为施工过程的荷载时间和冲击荷载。

其中：D()为爆破冲击荷载；为荷载常量；为荷载作用时间；B为爆破所采用的炸药的实测爆速为、炸药密度为0的炸药爆轰压力；e为爆轰速度；为爆心距与药包直径之比即比距离；为岩石泊松比；为爆孔装药质量；ge为炸药密度。各个参数的实测值如下：为3.6 km/s，0为1 g/cm³，为0.23，为28 kg。通过实测参数绘出的爆破冲击荷载时程曲线如图2所示。

图2 爆破冲击荷载时程图

2.2 阻尼比等参数的确定

由于岩土材料内部的摩擦以及接触表面的滑动阻尼会迫使地表质点振动的幅值随时间的增大而不断衰减，此外，数值模拟软件FLAC3D采用求解动力问题的方法需要使用阻尼来解决动力问题，所以，阻尼的确定对于解决动力问题至关重要。然而，典型结构体系的阻尼特性难以确定，为此，采用自由振动条件下具有相同衰减率的等效黏滞阻尼比来表示实际阻尼。在采用FLAC3D软件进行计算动力荷载分析时可采用瑞利阻尼。瑞利阻尼的2个参数分别为最小临界阻尼比和最小中心频率。

对自振频率下的位移时程曲线选取相邻的峰值作为1个振动周期，通过位移时程曲线可以确定阻尼比和中心频率，计算式为[15]：

式中：D0为阻尼比；A和A+1分别为第和第+1周的幅值；为振动周期；为振动频率。利用FLAC3D软件建立数值计算模型，不设置阻尼，在重力作用下求解。模型产生振荡，记录模型地表面关键节点的位移时程图，并输出自振频率计算得到的位移时程曲线，如图3所示。从图3可以确定最小临界阻尼比为2.01%，最小中心频率为11.44 Hz。

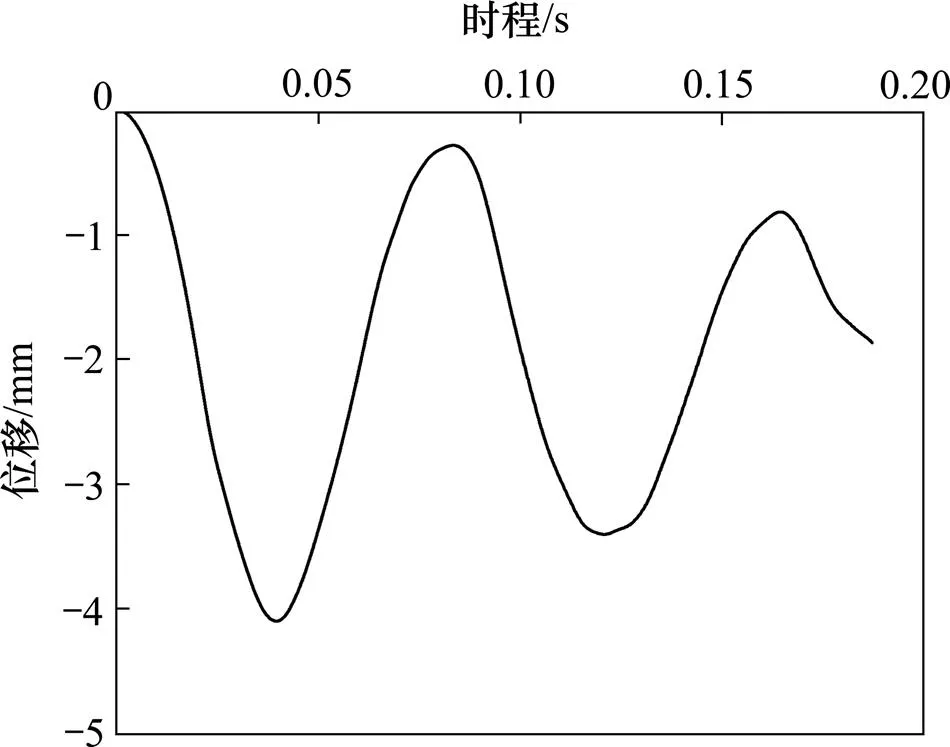
图3 重力荷载下地表位移时程图

2.3 监测点的布设

在隧道爆破开挖时，隧道开挖区上方地表沉降幅度大，远离开挖区的地表沉降较小，所以，在进行地表位移沉降监测时，采用如图4所示的监测点布设方式布设，即以隧道左右两线的中点为对称点，在对称点左右两端12 m的范围内，每相隔1 m设置1个监测点；在距对称点12～24 m范围内，每隔2 m设置1个监测点；在距离对称点24以外的范围，每隔5 m设置1个监测点。

图4 地表监测点的布设形式

3 分析与讨论

3.1 隧道单线爆破开挖地表位移沉降分析

对隧道的左、右两线单独进行爆破开挖，将图4所示监测点的布设形式分别布设在隧道爆破开挖的掌子面、距爆破开挖掌子面的未开挖区和已开挖区各 5 m的地表处，对地表位移沉降进行数值模拟分析，所得地表各点的位移沉降如图5~7所示。左右两线爆破开挖的沉降关于轴线对称。

从图5~7可见：隧道单线爆破开挖时地表位移沉降规律呈现单峰形式，左右两侧并不对称，地表沉降最大值均发生在隧道爆破开挖处上方，与隧道爆破开挖处的距离越大，地表的位移沉降越不明显；当距隧道爆破开挖处3倍洞跨时，地表位移沉降出现拐点。伴随沉降拐点的出现，隧道开挖基本上不会引起地表的位移沉降。

1—左线开挖掌子面上方竖向位移；2—右线开挖掌子面上方竖向位移

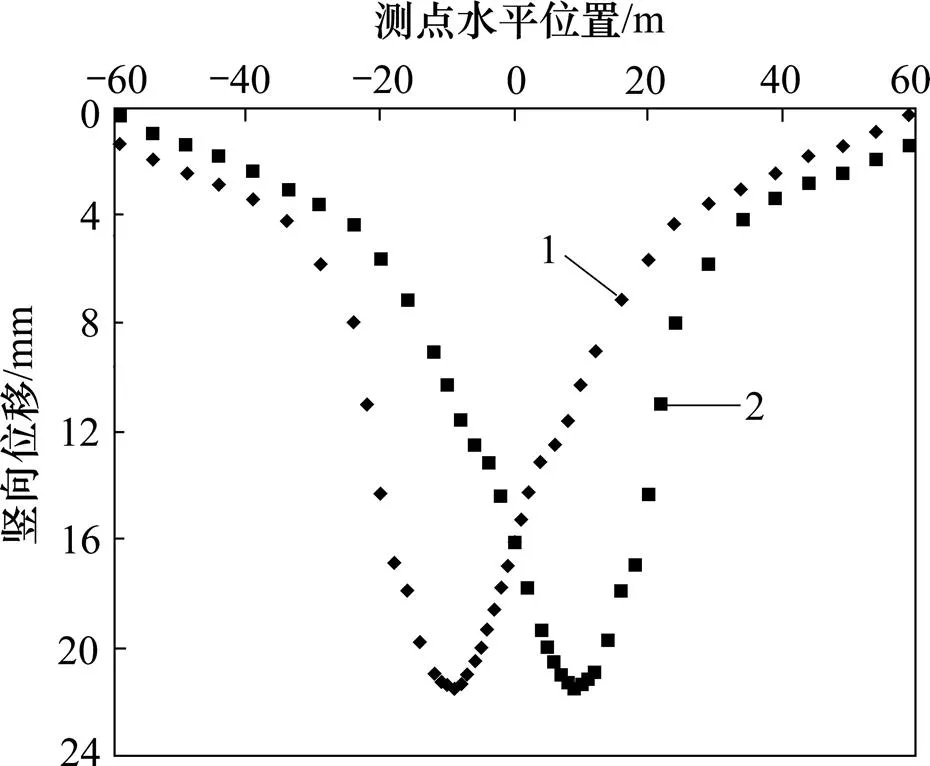
1—左线开挖距掌子面5 m开挖区竖向位移；2—右线开挖距掌子面5 m开挖区竖向位移

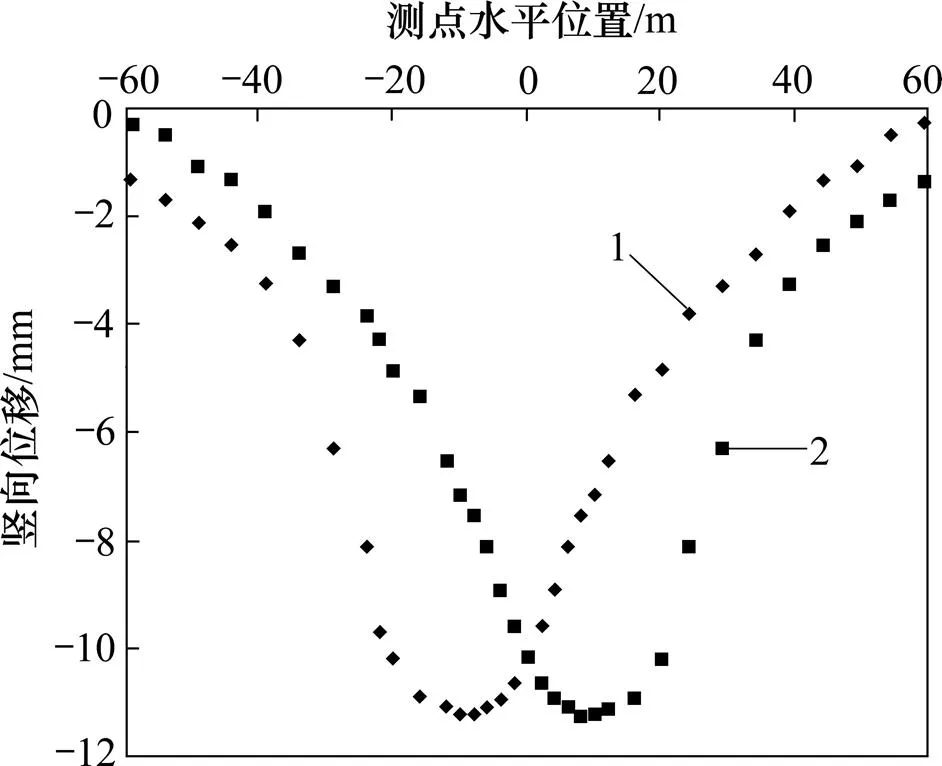
1—左线开挖距掌子面5 m未开挖区竖向位移；2—右线开挖距掌子面5 m未开挖区竖向位移

沿着隧道掘进方向，隧道开挖引起的沉降有所不同：在隧道爆破开挖区距掌子面5 m处地表位移沉降最大值为21.48 mm，掌子面上方的地表沉降最大值位移为18.48 mm；未开挖区距掌子面5 m处地表位移沉降最大值为11.26 mm。这说明隧道爆破开挖对隧道已开挖区上方和掌子面地表沉降的影响较大。

3.2 隧道双线爆破开挖引起地表位移累计沉降

对于本文研究的城际快速轨道依托工程，隧道设计为左、右2线，所以，隧道施工引起的地表位移沉降是两线隧道施工引起的地表变形相互叠加而形成的。双线隧道施工引起的地表变形要比单线隧道施工引起的地表变形复杂得多。双线隧道施工顺序是先对其中1条线隧道施工，完工后待其沉降稳定，再对第2条线的隧道进行施工。第2条线的隧道在施工时会对第1条线的隧道地表沉降产生一定影响，所以，在对隧道施工引起的地表位移沉降进行分析时，需要考虑隧道双线爆破开挖施工引起的地表位移累计沉降。隧道双线爆破开挖施工引起地表位移累计沉降如图8~11所示。从图8~11可见：从隧道未开挖区至隧道开挖区地表位移沉降规律由“单峰”形式逐渐向“双峰”形式转变，即地表位移最大沉降由两隧道中线向隧道洞口上方转移。

分别对比图5与图9以及图6与图10可知：左线开挖引起的地表沉降比待其沉降稳定后进行右线开挖引起的沉降更加明显；在左线开挖沉降稳定后的一段时间内，隧道围岩逐渐稳定；进行右线开挖时，引起的地表沉降较小。这符合工程实际情况。

图8 隧道双线爆破未开挖区距掌子面5 m处地表累计沉降

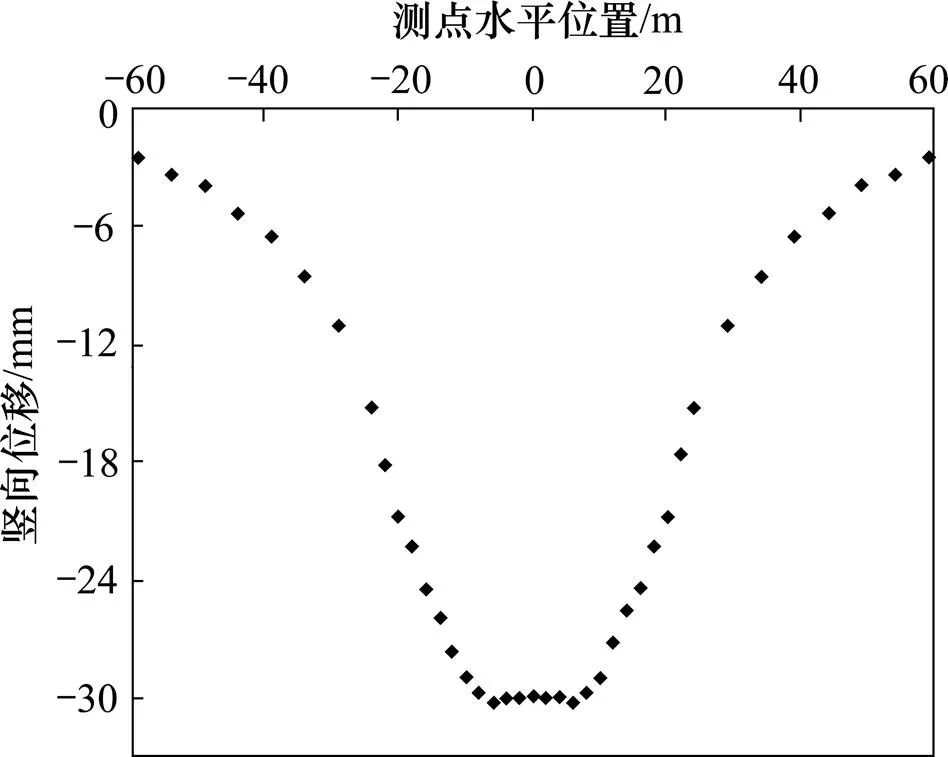
图9 隧道双线爆破掌子面地表累计沉降

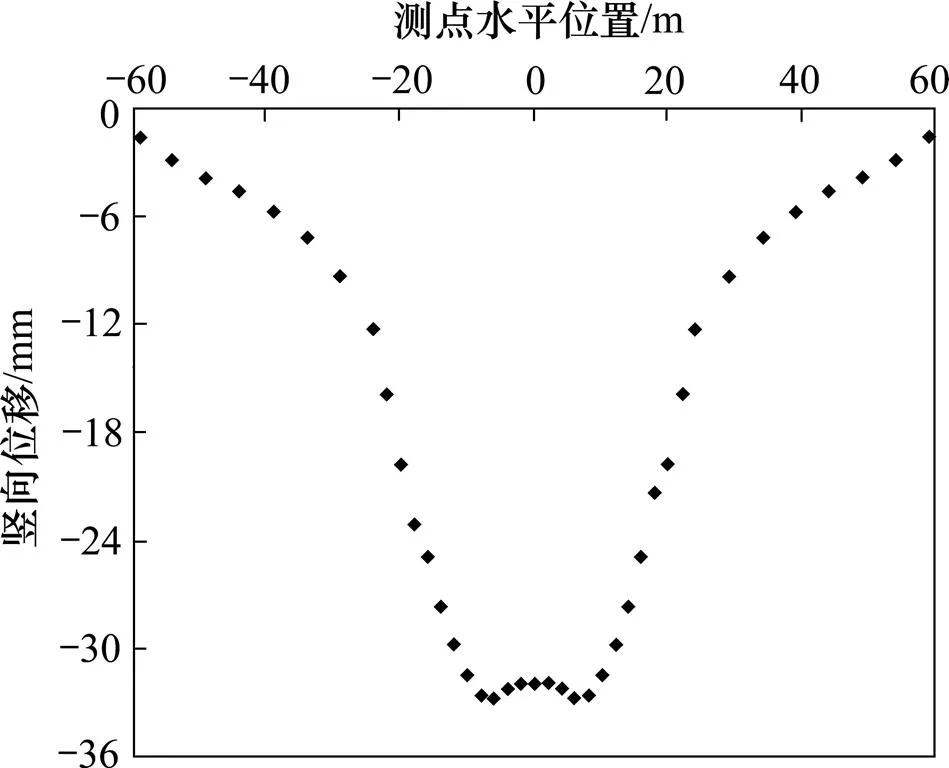
图10 隧道双线爆破开挖区距掌子面5 m处竖向位移

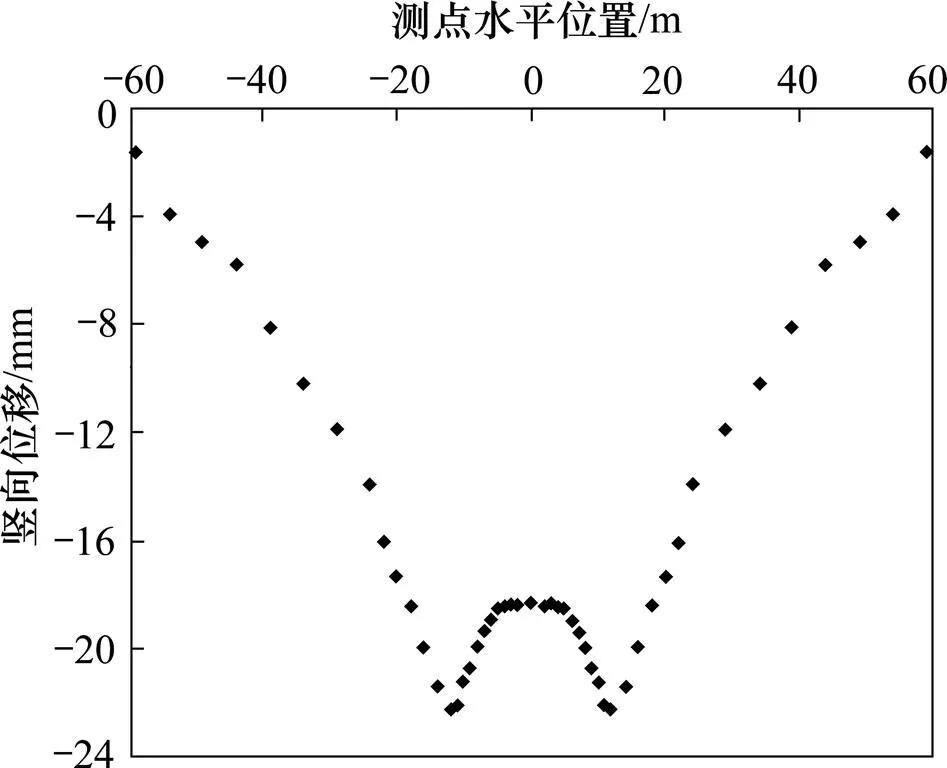
图11 隧道双线爆破开挖区距掌子面10 m处竖向位移

双线隧道在进行爆破开挖时对地表位移沉降影响较大区域位于隧道掌子面上方以及距掌子面一定范围内的隧道已开挖区上方，累计位移沉降值均在30 mm以上。随着离掌子面距离的增大，隧道爆破施工影响区的地表沉降变小；当距隧道掌子面在10 m以上时开挖区地表沉降在20 mm左右，其沉降远小于掌子面上方的地表沉降。

综上所述，在进行隧道爆破施工时，在隧道掌子面两端的开挖区和未开挖区的地表沉降对隧道爆破施工的响应不一致，开挖区的地表沉降大于未开挖区的地表沉降，并且在距离掌子面5 m处左右，沉降位移达到最大；随着开挖区距掌子面的距离增大，其地表的最大位移沉降点由隧道左、右两线中心向隧道左右两线上方转变。

3.3 隧道开挖地表水平位移分析

地表水平位移对建筑物、管线等也具有一定影响，尤其是水平位移对建(构)筑物的拉伸变形的影响，易使建筑物地基破坏、管线接头断裂等，因此，地表的水平位移监测及控制在施工过程中不容忽视。在隧道掌子面地表布设如图4所示的监测点监测地表水平位移，所得地表各点水平位移如图12所示。

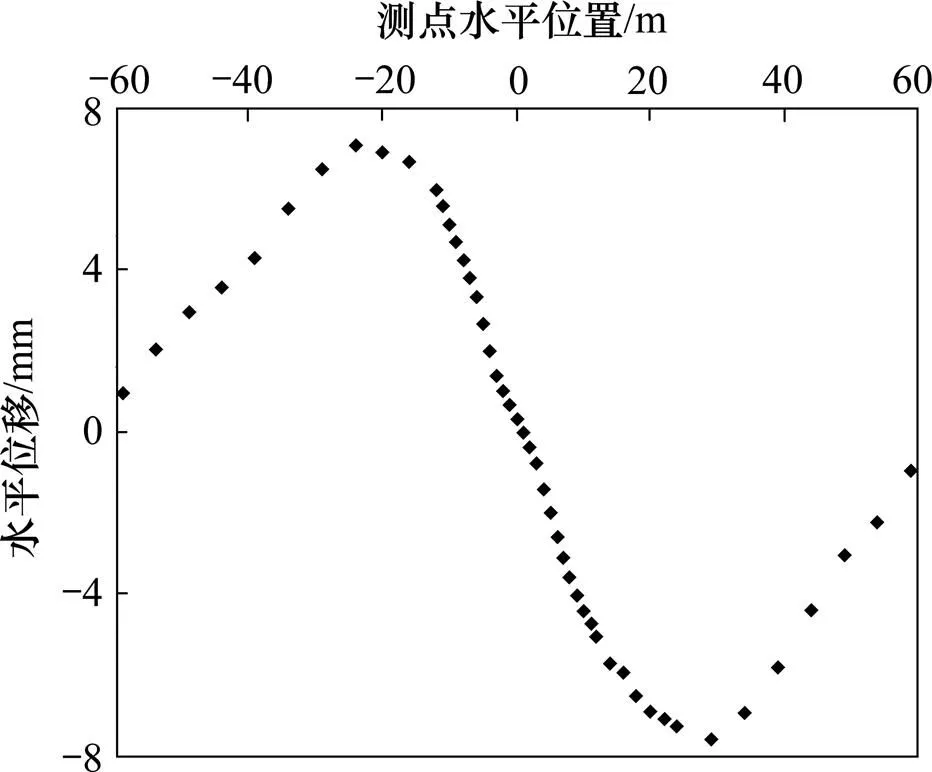
图12 隧道双线爆破掌子面地表水平位移

从图12可知：隧道爆破开挖后，随着与左右两线隧道中线距离减小，隧道上方地表水平位移先缓慢增大，在距隧道开挖上方2倍洞跨处水平位移达到最大值7.5 mm；随后迅速减小，直至在隧道中线地表处减小为0 mm，并在隧道中线两端呈现左右两边反向对称，即隧道上方的土体向隧道两线的中线运动。

4 结论

1) 隧道在进行单线隧道爆破开挖时，沿隧道掘进方向，地表位移沉降较大区域位于隧道掌子面以及距掌子面10 m内开挖区上方；垂直于隧道掘进方向，地表位移沉降较大区域位于隧道开挖区上方，沉降位移最大值达到21.48 mm，并且整个沉降规律呈现“单峰”形式。

2) 在单线隧道爆破开挖引起地表沉降稳定后进行第2条线隧道爆破开挖时，垂直于隧道掘进方向，从隧道掌子面到隧道开挖区上方，地表位移沉降的规律由“单峰”形式逐渐转变为“双峰”形式，即最大位移沉降点由两隧道中线上方向隧道开挖的上方转变，沉降位移最大值达到32.99 mm。

3) 双线隧道施工引起地表位移沉降与单线隧道施工引起的地表位移沉降相比，双线隧道施工引起的地表位移沉降规律更加复杂，地表沉降对其影响更加明显。

4)在隧道爆破开挖时，直至爆破开挖完成之后的一段时间，需要着重监测在距隧道开挖上方2倍洞跨处建(构)筑物的水平位移。在监测期间，若水平位移超过爆破规程的警戒值，则需要对建筑物采取加固 措施。

[1] 胡斌, 刘永林. 武汉地铁虎—名区间隧道开挖引起的地表沉降研究[J]. 岩石力学与工程学报, 2012, 31(5): 908−913. HU Bing, LIU Yonglin. Study on ground subsidence due to the tunnel excavation in Hu—Ming section of Wuhan subway[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 908−913.

[2] 贺农农, 李攀, 邵生俊, 等. 西安地铁隧道穿越饱和软黄土地段的地表沉降监测[J]. 地球科学与环境学报, 2012, 34(1): 96−103. HE Nongnong, LI Pan, SHAO Shengjun, et al. Ground displacement monitoring above Xi’an Metro tunnel through the saturated soft loess[J]. Journal of Earth Sciences and Environment, 2012, 34(1): 96−103.

[3] 缪林昌, 王非, 吕伟华. 城市地铁隧道施工引起的地面沉降[J]. 东南大学学报(自然科学版), 2008, 38(2): 293−297. MIAO Linchang, WANG Fei, LÜ Weihua. Ground surface displacement due to urban tunnel construction[J]. Journal of Southeast University (Natural Science Edition), 2008, 38(2): 293−297.

[4] 杨福麟, 刘永林, 胡斌. 武汉地铁隧道开挖引起地表沉降的数值模拟研究[J]. 工程地质学报, 2013, 21(1): 85−91. YANG Fulin, LIU Yonglin, HU Bin. Numerical simulation of ground subsidence due to tunnel excavation for Wuhan subway[J]. Journal of Engineering Geology, 2013, 21(1): 85−91.

[5] 肖欣欣, 李夕兵, 宫凤强. 隧道开挖及爆破对地表高压铁塔影响的FLAC3D分析[J]. 地下空间与工程学报, 2013, 9(6): 1401−1405. XIAO Xinxin, LI Xibing, GONG Fengqiang. Analysis of tunnel excavation and explosion influence on high-voltage tower with FLAC3D[J]. Chinese Journal of Underground Space Engineering, 2013, 9(6): 1401−1405.

[6] 张顶立, 李鹏飞, 侯艳娟, 等. 浅埋大断面软岩隧道施工影响下建筑物安全性控制的试验研究[J]. 岩石力学与工程学报, 2009, 28(1): 95−102. ZHANG Dingli, LI Pengfei, HOU Yanjuan, et al. Experimental study on safety control of buildings during construction of shallow-buried soft rock tunnel with large-section[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 95−102.

[7] 张顶立, 李鹏飞, 侯艳娟, 等. 城市隧道开挖对地表建筑群的影响分析及其对策[J]. 岩土工程学报, 2010, 32(2): 296−301. ZHANG Dingli, LI Pengfei, HOU Yanjuan, et al. Influence due to urban tunnel excavation on ground buildings and its countermeasures[J]. Chinese Journal of Geo-technical Engineering, 2010, 32(2): 296−301.

[8] 王利, 王海亮. 隧道爆破不同类型最大振动速度对建筑物的影响研究[J]. 爆破, 2012, 29(4): 6−9. WANG Li, WANG Hailiang. Influence of different direction vibration peak velocity of tunnel blasting on building[J]. Blasting, 2012, 29(4): 6−9.

[9] 喻军, 刘松玉, 童立元. 浅埋隧道爆破振动空洞效应[J]. 东南大学学报(自然科学版), 2010, 40(1): 176−179. YU Jun, LIU Songyu, TONG Liyuan. Hollow effect induced by blasting vibration in shallow tunnels[J]. Journal of Southeast University (Natural Science Edition), 2010, 40(1): 176−179.

[10] 朱才辉, 李宁, 柳厚祥, 等. 盾构施工工艺诱发地表沉降规律浅析[J]. 岩土力学, 2011, 32(1): 158−164. ZHU Caihui, LI Ning, LIU Houxiang, et al. Analysis of ground displacement induced by workmanship of shield tunnelling[J]. Rock and Soil Mechanics, 2011, 32(1): 158−164.

[11] 李新志, 李术才, 李树忱. 浅埋大跨度隧道施工过程地表沉降变形特征研究[J]. 岩石力学与工程学报, 2011, 30(1): 3343−3358. LI Xinzhi, LI Shucai, LI Shuchen. Ground displacement deformation characteristic study of shallow large-span tunnel in construction process[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 3343−3358.

[12] 周丁恒, 曲海锋, 蔡永昌,等. 特大断面大跨度隧道围岩变形的现场试验研究[J]. 岩石力学与工程学报, 2009, 28(9): 1773−1782. ZHOU Dingheng, QU Haifeng, CAI Yongchang, et al. In-situ test on surrounding rock deformation in super-large section and large-span tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1773−1782.

[13] 段宝福. 工程爆破[M]. 北京: 北京大学出版社, 2012: 137−140. DUAN Baofu. Engineering blasting[M]. Beijing: Peking University Press, 2012: 137−140.

[14] 王祥秋, 周岳峰, 周治国. 爆破冲击荷载下隧道振动特性与安全性评价研究[J]. 中国安全科学学报, 2011, 11(5): 134−138. WANG Xiangqiu, ZHOU Yuefeng, ZHOU Zhiguo. Study on vibration characteristics and safety of tunnel under blasting impact load[J]. China Safety Science Journal, 2011, 11(5): 134−138.

[15] Clough R W, Penzien J. 结构动力学[M]. 王光远, 译. 北京: 高等教育出版社, 2013: 29−34. Clough R W, Penzien J. Dynamics of structures[M]. WANG Guangyuan, trans. Beijing: Higher Education Press, 2013: 29−34.

(编辑 陈灿华)

Numerical simulation of ground subsidence due to tunnel blasting excavation

HE Zhongming1, 2, CAI Jun2, WANG Lijun3, LUO Xin3, WEI Xiaobo3

(1. Key Laboratory of Special Environment Road Engineering of Hunan Province, Changsha University of Science & Technology, Changsha 410114, China;2. School of Traffic and Transportation Engineering, Changsha University of Science and Technology,Changsha 410114, China;3. Construction Headquarters of Guangzhou Metro Corporation, Guangzhou 510380, China)

Based on the project of intercity rapid track section of Guangzhou to Foshan in Pearl river delta, the FLAC3Dsoftware was used to build the model of tunnel excavation. Surface subsidence caused by tunnel blasting excavation was computed, and the regulation of the surface subsidence was analyzed. The results show that the tunnel blasting excavation has impact on the surface subsidence from a certain range of excavation area to excavated face after applying the blast load on the tunnel wall. When the second tunnel is excavated, the maximal displacement displacement position of tunnel surface moves from the center line of the two tunnels to the tunnel; after the surface subsidence of the first excavates tunnel reaches stable, the magnitude of displacement is related to the distance between the excavated zone and the excavated face. The shorter the distance, the larger the displacement of the surface.

tunnel; blasting excavation; ground subsidence; impact load

10.11817/j.issn.1672-7207.2015.09.045

TU94+1

A

1672−7207(2015)09−3496−07

2015−01−07；

2015−03−22

国家自然科学基金资助项目(51478054)；广州市地下铁道总公司科研项目(HT141595)；长沙理工大学特殊环境道路工程湖南省重点实验室开放基金资助项目(kfj140501) (Project(51478054) supported by the National Natural Science Foundation of China; Project(HT141595) supported by Guangzhou Metro Corporation; Project(kfj140501) supported by Open Fund of Key Laboratory of Special Environment Road Engineering, Changsha University of Science & Technology)

何忠明，博士(后)，副教授，从事道路工程、防灾减灾工程的教学研究工作；E-mail: hezhongming45@126.com