基于L型阵的二维Root－MUSIC波达方向估计算法

张 虎，仝 侨

(西安电子科技大学电子信息攻防对抗与仿真重点实验室，陕西西安 710071)

波达方向(DOA)估计在电子侦察、智能天线、雷达、声纳等领域的应用已经成为目前研究的热点［1－2］，在进行二维DOA估计时，一般采用平面阵，而平面阵的结构比较复杂，且阵列的冗余度较大。二维MUSIC算法是二维DOA估计的典型算法［3］，这种方法可以产生渐近无偏估计，但要在两个方位上进行搜索谱峰，计算量大［4］。而 Root－ MUSIC［5］用多项式求根的方法代替了谱峰搜索，且比MUSIC算法具有更像且更低的分辨力门限和估计方差［6］。

L阵传统估计方法将其所有阵元接收数据作为一个整体进行二维MUSIC谱峰搜索，需要扫描两个角度，计算量大，影响系统的实时性。由于线阵方向估计研究比较成熟，而L阵又是线阵垂直叠加而成。在不改变传感器阵形的条件下，借助线阵Root－MUSIC方法将二维平面谱峰搜索分为两个独立线阵一维角度估计，这将大幅压缩计算量，且解决了测向精度和系统稳定性的问题。

1 阵列结构和信号模型

图1为二维方向估计的空间模型，阵列是由x子阵和y子阵构成的L型阵列，两个直线阵阵元分别沿x轴和y轴均匀排列，阵元个数均为M+1个。子阵阵元间距均为，来自远场目标辐射的信号入射到阵面上。假设其方位角和俯仰角分别为(α，β)，则入射方向余弦为(sinβcosα，sinβsinα，cosβ)。

假设入射到此阵列上的信源数为K，则x子阵和y子阵接收的信号可以表示为

图1 L型阵列结构图

式中，S=［s1(t)，…，sk(t)］T，Ax=［ax(α1，β1)，a2(α2，β2)，…，ax(αk，βk)］，ax(αk，βk)=［1，u(αk，βk)，…，uM+1(αk，βk)］T，u(αk，βk)= exp(j2πd sinβkcosαk/λ)，Ay=［ay(α1，β1)，ay(α2，β2)，…，ay(αk，βk)］，ay(αk，βk)=［v(αk，βk)，v2(αk，βk)，…，vM+1(αk，βk)］T，v(αk，βk)=exp(j2πd sinβksinαk/λ)，k=1，…，K，S是接收数据矩阵，Nx、Ny是接收噪声，Ax∈CM×K，Ay∈CM×K，d= λ/2，λ 是信号波长。T 表示转置，接收噪声是均值为0，方差为σ2的加性高斯白噪声，0≤α≤π，0≤β≤π/2。

2 方位角和俯仰角估计算法

L阵的阵列流形为

该L阵得到的信号自相关矩阵为

其中，RXX=E{X(t)XH(t)}=AxPAHx+σ2I，RYY=E{Y(t)YH(t)}=AyPAHy+ σ2I，RXY=E{X(t)YH(t)}=AxPAHy，σ2为噪声方差，H表示矩阵共轭转置，P为信号相关矩阵，RXX、RYY为两子阵采样数据的自相关矩阵，RXY为两子阵互相关矩阵。

对RXX进行Root－MUSIC得到K个方向余弦值的估计

同样，对RYY进行Root－MUSIC可以得到K个方向余弦值的估计

其中，k=1，…，K，由于两个线阵是独立进行估计的，当目标个数多于一个时，就会有配对问题，即有K!种组合方式，而其中只有一种组合方式实际存在。

对RL特征值分解得到

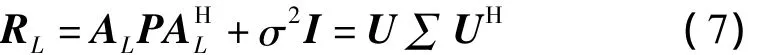
在正确配对后，根据图1中的几何关系可以得出

从而得到正确的方位角和俯仰角

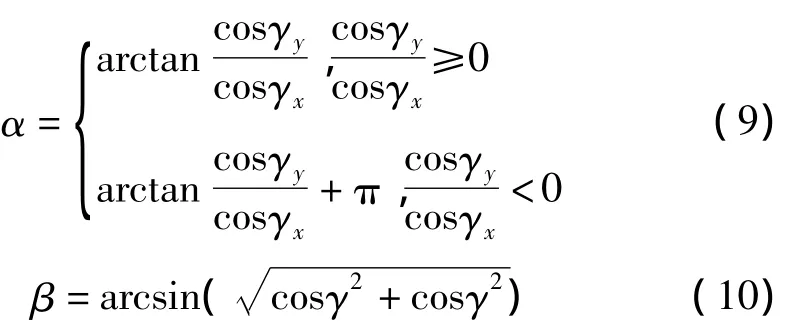
3 计算机仿真实验

实验1 为验证上述方法的有效性，仿真实验如下。取快拍数512次，目标数K=2，两子阵阵元个数均为 9 个，目标方位角和俯仰角为(30°，30°)和(40°，40°)，信噪比取10 dB，进行100次仿真，估计性能如图2所示。从图中可以看出，该方法可以精确地估计出目标方位。

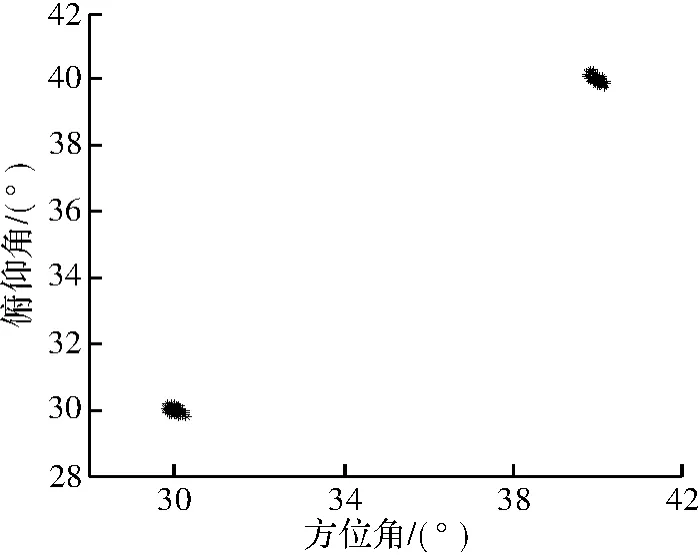
图2 SNR=10 dB时的二维DOA估计性能

实验2 将本算法与文献［7］进行比较，取目标方位为(30°，30°)，两子阵阵元个数均为 9个(即 M=8)。进行100次独立重复试验，定义估计误差RMSE=，其中θm是第m次估计的方位角或俯仰角。方位角和俯仰角估计误差随信噪比的关系曲线如图3所示，将二维MUSIC分解成两个一维的Root－MUSIC后，与文献［7］中的算法相比，方位角估计误差相差不大，但俯仰角估计误差却有所降低，可见本算法优于文献［7］中提出的算法。

实验3 为确定本算法与文献［7］算法的估计误差随阵元个数变化的关系，取SNR=5 dB，其它条件与实验2相同，得到结果如图4所示，随着阵元数的增加，本文算法估计误差要小于文献［7］算法的估计误差［8－9］。

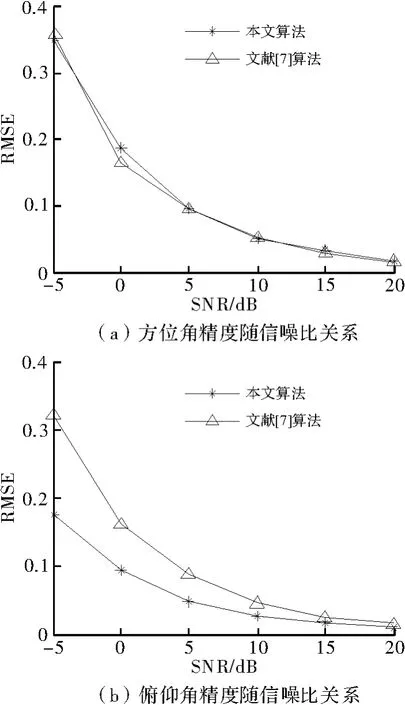
图3 二维DOA为(30，30)时的估计性能比较

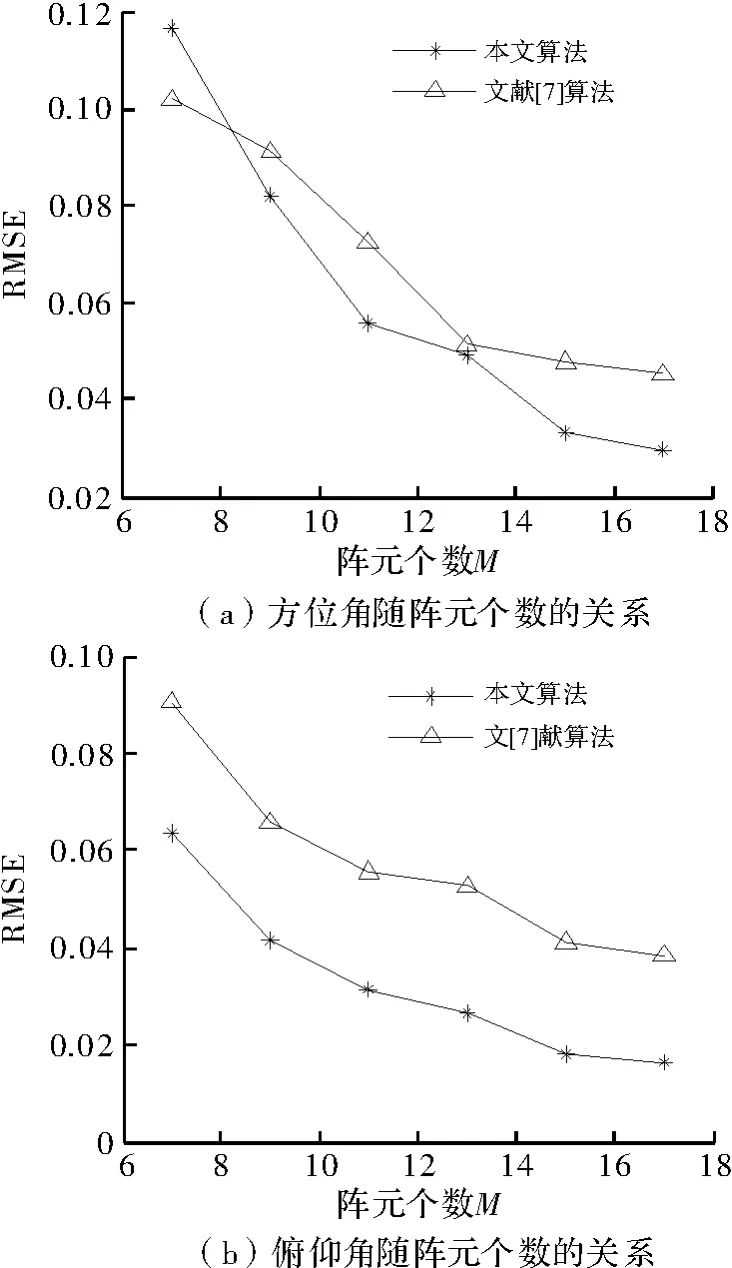
图4 估计误差随阵元个数的关系

4 结束语

二维MUSIC算法是二维DOA估计的典型算法，这种方法可以产生渐近无偏估计，但在要二维参数空间搜索谱峰，计算量较大，影响了该算法的实用性。理论分析和仿真表明，本文提出的方法是有效的，此方法所应用的阵列结构为L型，运算量较低精度较高，具有一定的实用性。

［1］Belouchrani A，Amin M G.Time － frequency MUSIC［J］.IEEE Signal Processing Letters，1999，6(5):109 －110.

［2］Sathish Chandran，Mohammad K.Ibrahim.DOA estimation of wide－ band signals based on time － frequency analysis［J］.IEEE Journal of Oceanic Engineering，1999，24(1):116 －121.

［3］Wax M，Shan T J，Kailath T.Spatial－ temporal spectral analysis by eigenstructure method ［J］.IEEE Transactions on ASSP，1984，32(4):817 －827.

［4］张小飞，汪飞，徐大专.阵列信号处理的理论和应用［M］.北京:国防工业出版社，2010.

［5］Barabell A J.Improving the resolution performance of eigenstructure based direction finding algorithms［C］.Boston，MA:Proceeding of IEEE ICASSP －83，1983:336 －339.

［6］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.

［7］陈建.二维波达方向估计理论研究［D］.吉林:吉林大学，2006.

［8］杨晓玉.冯大致.Esprit算法在单基地MIMO雷达中的应用［M］.电子科技，2009(12):91－94，99.

［9］郭艺夺，张永顺，童宁宁，等.一种MIMO雷达DOA估计新算法［J］.电波科学学报，2010(4):668－673.