基于改进蜂群算法的神经网络及其应用

(广西幼儿师范高等专科学校 公共基础部，广西 南宁530022)

0 引言

目前，数值天气预报模式的预报能力已经有了长足的发展，对于利用各种模式的输出产品资料进行站点强降水过程的预报研究是一项重要课题.因此，找出众多的模式预报产品与预报站点之间的某些非线性关系，是天气预报数值预报产品试用的一条有效途径.为此，很多学者开展了利用人工神经网络方法拟合出多种数值预报产品与预报站点的非线性关系，并利用这一关系进了有关的降水预报［1－3］.然而，神经网络预报能力的强弱与神经网络的训练是否充分有很大关系，因此，网络权值的训练方法对神经网络的泛化能力有着决定性的影响.但是，一般的BP 神经网络训练都是基于梯度下降的训练方法，该训练方法对给定的初始权值敏感性强，收敛速度缓慢且容易陷入局部最优，从而导致BP 神经网络的预测可靠性降低［4］.

人工蜂群算法［5］(artificial bee colony algorithm，ABC)是根据蜜蜂群中个体间相互协作进行搜索花粉的行为而提出的一种优化算法，它具有很强的全局搜索性能.尽管，蜂群算法研究和应用的时间不长，但由于算法参数少、易于实现等优点，使越来越多的学者对它进行了研究［6－8］.2009年，Karaboga 等人完成了利用ABC 算法来训练神经网络［9］，并取得了较好的效果.然而，ABC 算法也存在当算法搜索到全局最优解附近时，算法收敛速度变慢或停滞不前的早熟现象问题.为此，本文对标准的人工蜂群算法进行了改进，可以加快算法的收敛速度，同时也能提高算法的收敛精度.

本文利用这种改进的蜂群算法来训练神经网络的连接权，其实际应用的结果显示，通过这种方法训练出来的神经网络具有更好的泛化性能.

1 改进的蜂群优化算法

1.1 蜂群算法及其改进

蜂群算法是一种集群智能算法，其特点是可以在不清楚问题的特殊信息条件下，仅利用人工蜂个体对问题评价的优劣进行比较，通过蜂群个体的邻域寻优行为，最终全局最优解在整个蜂群的优劣比较中显现出来.ABC 算法中种群的个体分为引领蜂、跟随蜂和侦查蜂三个类别，每一个种类的觅食行为都有区别.首先，引领蜂随机出去寻找蜜源，找到蜜源之后返回巢穴通过舞蹈的方式将关于蜜源的信息(包括蜜源离巢穴的距离、方位以及蜜源花蜜数量的多少)传递给在巢穴前等候的跟随蜂;其次，跟随蜂根据引领蜂传递给的信息选择哪个引领蜂发现的蜜源去采蜜，而侦查蜂是某处一蜜源因为其花粉数量太少而被引领蜂和跟随蜂都抛弃之后，由发现该蜜源的引领蜂转变而来.其中，引领蜂和跟随蜂位置的更新公式:

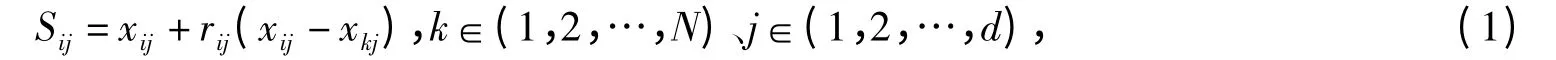
其中k，j 是随机给定的，且k≠j(k 是i 邻域的一个解)，随机数rij∈［－1，1］.该参数用于控制引领蜂和跟随蜂的蜜源邻域搜索.

本文对ABC 算法作的改进如下:

①除去跟随蜂根据引领蜂觅食回来提供的蜜源信息而选择哪个蜜源的搜索过程，从而减轻算法的计算量;

②记录并更新每一轮搜索后的目前为止发现蜜源质量最好的引领蜂记为pg，用于向其他引领蜂分享花蜜信息;

③添加一个上一轮的位置对当前位置影响大小为ω 的参数;

④采取多点(1＜m≤5)位置同时更新.在ABC 算法中，每个引领蜂位置的更新都是随机给定的一个点，这样是为了防止算法出现早熟，但同时也使算法收敛速度变慢，本文则在d 个位置中随机给出m 个位置同时更新.

⑤引领蜂的搜索邻域进行自适应调整，即开始的搜寻阶段搜索范围较大，而在搜索后期搜索的邻域则逐渐缩小范围，这样有利于算法的局部搜索.

⑥引领蜂的位置更新公式改成:

其中:

而(2)式中的ω 和v 的数学描述为

其中kg=0.25－0.5* (maxT－t)/maxT 为0.25～0.75 线性递增，k≠i，j=unidrnd(d，1，m)为在1－d 间随机产生m 个整数.

改进算法的具体实现步骤如下:

1)给定算法的参数:种群数量Nm和最大迭代次数Gmax;

2)在解空间范围内随机生成m 个个体的初始位置;

3)计算每个个体的适应值;

4)求出种群的最优位置Pg.

开始进行迭代搜寻:

5)对于种群中的每一个个体，记为i(i≤Nm)

①1－d 在之间随机生成m 个互不相同的数，记为j=(j1，j2，…，jm);

②在1－Nm之间生成一个不等于i 的数，记为K;

③按(2)式更新第i 个引领蜂的位置j;

④对更新的位置超出搜索边界上限等于上限减去一个很小的值;

⑤对更新的位置超出搜索边界下限等于下限加上一个很小的值;

⑥计算适应度值Fitness(s);

⑦比较第i 个引领蜂更新前后适应度的大小，取适应度大的作为该引领蜂当前的位置，同

时更新该引领蜂的累计不变参数Ⅰt;

⑧判断第i 个引领蜂的适应度与是否比Pg的适应度大，若是，则更新Pg.

6)完成一轮搜索后，如果有引领蜂的累计不变参数“Ⅰt”达到最大容忍值，则放弃该引领蜂，并按公式(4)随机生成一个侦察蜂替它，此时Ⅰt 归零;

7)判定搜索结束条件，若满足，则输出最优值，否则转到5).

1.2 改进的蜂群算法性能测试

为了验证本文提出的新的蜂群算法(NABC)的性能，本文选取了多个经典测试函数对新算法进行测试，其表达式如下所示，并将之与标准人工蜂群(代码来源于Karaboga 等人主页提供的ABC 算法代码)的结果进行比较.所用的测试函数及其寻优的范围、最优点、初始化范围等信息如下:

1)Sphere 函数

2)Ackley 函数

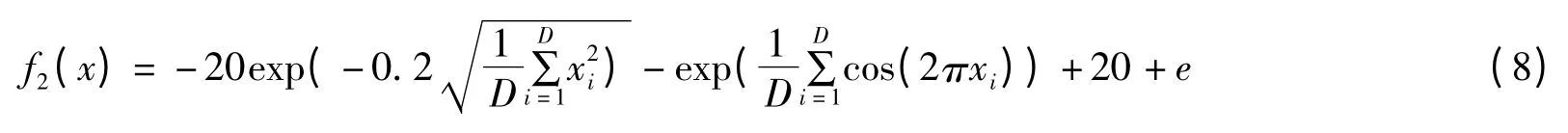
3)Griewanks 函数

4)Weierstrass 函数

5)Rastrigin 函数

表1 测试函数的全局最优点、搜索范围以及初始化范围

在改进算法中，实验计算种群规模Nm=50;最大迭代次数2000 次;控制参数Ⅰt 为100.对于ABC 算法，种群规模也50，参数Ⅰt 为100;最大迭代次数2000 次.每个函数独立运行20 次，其比较结果见表2.

从表2可以看出，本文提出的NABC 算法的收敛精度远高于标准的ABC 算法，而且在5 个100 维的测试函数中，本文提出的算法有3 个函数搜索到理论最优解，还有一个函数(Sphere 函数)其精度也几乎达到了理论值，从而表明了本算法的稳定性和有效性.图1为本文的算法和ABC 在300 维的rastrigin 函数在迭代过程中适应度值的变化情况.

表2 函数为100 维的测试结果

表3 函数为200 维的测试结果

从图1可以看出，本文提出的算法在进行全局寻优时，其收敛速度明显快于ABC 算法，同时收敛的精度更高.

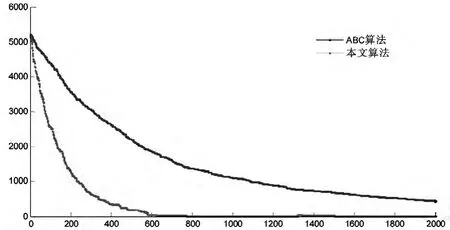
图1 本文提出算法和ABC 算法对300 维rastrigin 函数收敛曲线

2 改进的蜂群算法训练BP 网络

将NABC 算法用于BP 网络的训练:蜂群中每个引领蜂的位置由BP 网络结构各层连接权和阈值按顺序排放组成，其维数是所有权值和阈值的数量，即一个引领蜂就表示一组神经网络的权值.而神经网络对训练样本集的拟合均方根误差(MSE)则作为NABC 算法的适应度值，如果某一个引领蜂的适应函数值越小，则表明该引领蜂在搜索中具有更好的权值分布.通过这种方式，NABC 算法在不断搜索和优化训练神经网络的连接权的过程中，不断地获得更小的神经网络对训练样本拟合的平均绝对误差(MSE)，而算法在搜索过程中不断更新最小 的MSE 值，并将具有最小MSE 的引领蜂的位置记为Pg.

3 基于NABC-BP 的实验及结果分析

为了测试经NABC 算法训练的神经网络的泛化性能，本文以南宁市2010－2013年6－8月的逐日降水作为预报对象，并以同期的欧洲细网格雨量资料和粗网格的物理量场资料作为模型的预报因子资料.

我们首先通过对预报因子历史资料与预报对象进行相关普查，对于相关系数大于0.25 的雨量格点因子直接作为模型预报因子的一部分，另一部分则是物理量因子，即在大范围相关系数较高的物理量场格点中，选出相关系数最大的2 个相邻格点的平均值作为模型输入的物理量因子.最终，由雨量资料和物理量因子资料共11 个因子作为降水预测模型的输入因子.于是，利用第2 节的NABC 训练神经网络的方法，对2013年6－8月份的南宁市的逐日平均降水量进行独立预报试验.同时为了考察本文提出方法的预报效果，论文也对ABC 训练神经网络(记为ABC－BP 方法)预报方法进行相同的预报试验，见表4.

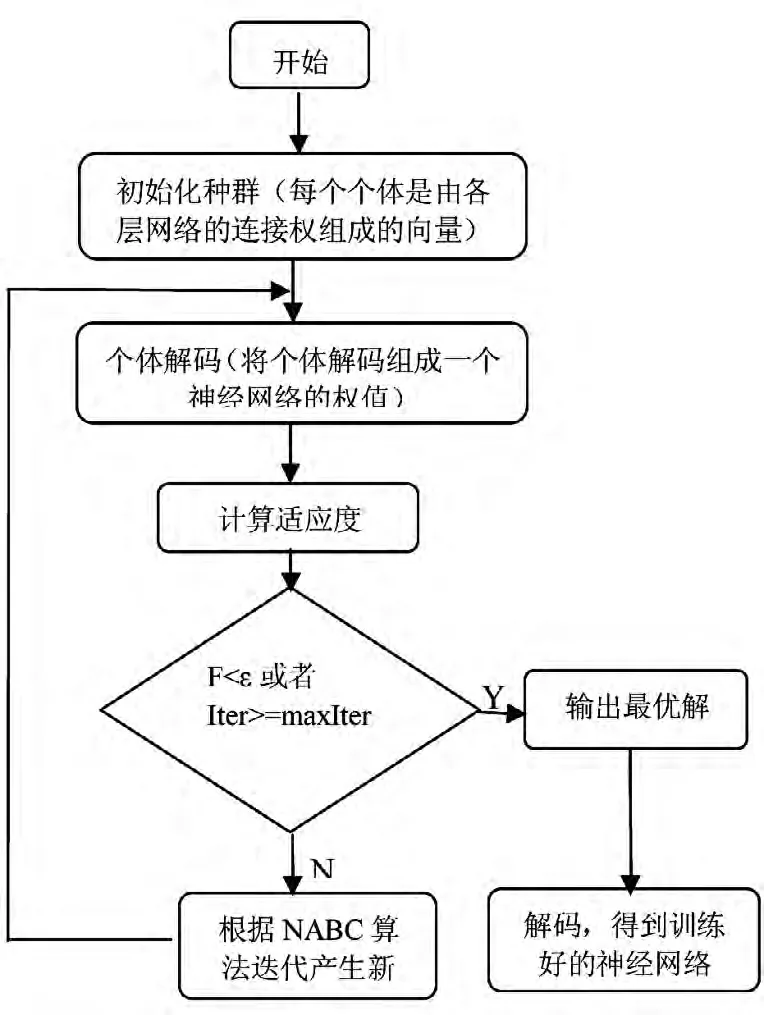
图2 NABC－BP 算法流程

表4 南宁市2013年6－8月份降水量TS 评分

其中TS 的评分规则是:

从表4可以看出，经过NABC 算法训练的神经网络，其训练更加充分，预报能力比ABC 算法训练的神经网络更强，特别是对暴雨和暴雨以上雨量的预报情况，其TS 评分提高了17.6%和30.7%，同时该算法的预报能力也比欧洲中心细网格雨量插值强，这表明，本文提出的基于NABC 的神经网络训练方法是有效的，可以应用于实际业务预报.

4 结语

本文为了使神经网络的训练更加充分，首先提出了一种新的蜂群算法(NABC)，该算法简化了标准人工蜂群算法的搜索过程，并在算法的更新方法上尝试了多点位置同时更新，进一步地，本文改变了标准人工蜂群算法中引领蜂的邻域搜索均在［－1，1］中随机产生的方法，而是根据算法的搜索进程进行自适应改变，使算法在搜索初期引领蜂的搜索邻域大些，而文后期则小些，这样可以使算法在搜索初期选择的范围更大、更有利于找到更好的解，而搜索范围较小的搜索后期则有利于算法局部收敛.该改进的算法无论是在多极值函数的全局寻优上还是在训练神经网络的权值上，改进的蜂群算法都具有收敛速度快而且收敛精度极高的特点，经该算法训练的神经网络泛化能力也更加强，并在降水的实验预报中显示了该方法的有效性和实用性.

［1］农吉夫，黄文宁.遗传算法优化神经网络的汛期降水模型［J］.数学的实践与认识，2010，40(20):54－58.

［2］林建琳，金龙，林开平.神经网络方法在广西日降水预报中的应用［J］.南京气象学院学报，2006，29(2):215－219.

［3］赵华生，金龙，农吉夫，等.降水预报的神经网络集成方法的改进［J］.统计与决策，2008(10):26－28.

［4］高海兵，高亮，周驰，等.基于粒子群优化的神经网络训练算法研究［J］.电子学报，2004，32(9):1572－1574.

［5］Karaboga D.An idea based on honey bee swarm for numerical optimization，Technical Report－TR06［R］.Kayseri:Erciyes University.Engineeirng Faculty，Computer Engineering Department，2005(9):1572－1574.

［6］Srinivasar R，Narasimham S，Ramalingara J.Optimization ofdistirbution network conifguration forloss reduction using artificial bee colony algorithm［J］.Intenrational Joumal of Electrical Power and Energy Systems Engineering，2008，1(2):709－715.

［7］Singha.An atriifcial bee colony algorithm for theleaf－constrained minimum spanning treeproblem［J］.Applied Sotf Computing，2009，9(2):625—631.

［8］丁海军，李峰磊.蜂群算法在TSP 问题上的应用及参数改进［J］.中国科技信息，2008(3):241－243.

［9］Karaboga D，Ozturk C.Neural networks training by artificial bee colony algorithm on pattern classification［J］.Neural Network World，2009，19(3):279－292.