基于群签名的安全电子招投标方案

(滁州职业技术学院 经济贸易系，安徽 滁州239000)

0 引言

随着政府信息化建设的大力推广，电子招投标已经是势在必行.通过网络方式来招投标，可以使招标人、投标人和评标专家进行有效隔离.与传统的人工方式招投标相比，电子招投标可以有效防止招标人、投标人、评标专家之间的“串标”行为，也可以防止招投标管理机构的权力过于集中而导致的舞弊行为.同时，还可以节约大量的人力、物力和财力，有效降低招投标的成本，提高招投标的工作效率.

本文所设计的电子招投标方案是基于双线性对的群签名技术，关于群签名的设计，文献［1］利用的是ACJT 群签名方案，该方案的抗联合攻击能力较强，其安全性已经得到有效证明，然而该方案在密钥管理方面还存在许多不足之处，其公钥长度也相对比较长.文献［2］是在基于双线性对和判定线性假设的基础上提出短群签名方案，该方案相对其他方案来说，其最大优势就是大大缩短了其签名长度，但该方案的签名却无法打开.为此，本文在文献［3］基础上，对文献［4－6］进行综合改进和优化，提出一种新的安全电子招投标方案.该方案引入矢量空间秘密共享技术和阈下通道技术，同时本方案可以增删成员，其签名的公钥长度是完全独立的.

1 预备知识

1.1 群签名

群签名(Group Signature)是由Chaum 和Heyst 于1991年首次提出此概念，其构造主要是基于离散对数问题.2002年，Hess 利用双线性对构造了一个群签名，从此，群签名的研究进入了一个比较活跃的时期.最近，文献［7］将群签名过程分为系统建立、成员加入、成员删除、签名过程、验证过程、签名打开共六个步骤.

1.2 双线性映射

假设G1是生成元P 的循环加法群，G2是其循环乘法群，其阶都是素数q，群G1、G2上的离散对数在计算问题上都是非常困难的［8］.现定义双线性对e:G1×G1→G2，e 需要满足如下三个条件:

(1)双线性:e(aP，bQ)=e(P，Q)ab=e(abP，Q)=e(P，abQ)，其中P，Q∈G1;a，b∈Z*q;

(2)非退化性:存在P∈G1，其满足e(P，P)≠1;

(3)可计算性:任意选取P，Q∈G1，存在一个有效算法，使其能计算e(P，Q).

1.3 矢量空间秘密共享

秘密共享是将某个需要处理的秘密k 分成为n 个子秘密，由n 个参与者共同来管理这n 个子秘密，n个参与者的集合P={p1，p2，…，pn}，其在授权子集内的成员可以通过协作的方式，利用自己的子秘密进行重构，生成秘密k，而任何不在授权子集范围内的非法成员不可能得到关于该秘密k 的任何信息.

矢量空间秘密共享描述如下:设Γ 是P 的子集，D 是可信赖的中心机构，且D∉P.q 为大素数，K=GF(q)，P∪{D}→K'，(K'表示K 上所有r 元构成的矢量空间)，φ(D)=(1，0，…，0)∈〈φ(pi)=(a1i，a2i，…，ari)∶pi∈A〉⇔A∈Γ.当对所有参与者pi∈P，有Sp∈K(Sp表示参与者pi可能接收到的所有子秘密集合)时，就可以建立一个理想的矢量空间秘密共享方案.

1.4 阈下通道技术

阈下通道技术是基于应用密码体制建立起来的一种隐蔽的秘密信息传输通道技术.利用阈下通道技术，其最大的好处就是除指定的接收者外，其他任何非授权用户或网络攻击者均难以发现该通道的存在，更不可能获取正在传送的阈下秘密信息内容.目前，常用的阈下通道技术采用的是基于椭圆曲线(t，n)门限签名方案，该阈下通道技术综合了门限方案和椭圆曲线数字签名方案的优点，其安全性可以得到有效保障.

2 基于双线性对群签名的电子招投标方案

2.1 方案的组成

电子招投标流程通常由发布招投标公告、投标人报名、资格审查、招标文件发放、网上答疑、缴纳与退还保证金、投标、开标、评标、确定中标人、公布中标结果等环节组成［9］.其涉及的人员主要包括注册中心、招标人、投标人、评标专家以及招投标管理机构，如图1所示.

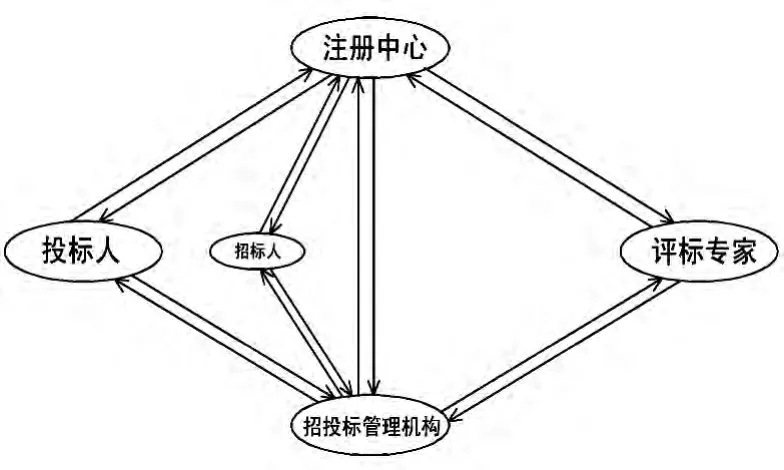
图1 电子招投标系统的人员组成

一个安全的电子招投标方案［10］，必须要满足以下几点:

(1)身份合法性:电子招投标系统必须经过相应的身份验证，只有合法的用户才能登录到该系统中去，任何非法用户无法登录至系统中，从而确保电子招投标工作能够安全开展.

(2)不可抵赖性:投标人在发送投标书后不能否认自己的投标行为以及所投标书的内容，同时招投标管理机构也不能否认自己在合法、有效的时间内收到投标人所投的标书.

(3)安全传输:在投标书传输过程中，要确保投标书的机密性和完整性，不能泄密投标书中的商业秘密，也不得篡改投标书中的相关内容.

(4)时效性:电子招投标系统必须要有招标截止时间限制，超出招标截止时间后的任何投标书一律无效，这样就必须要确定投标人提交投标书的确切时间，以确保投标人的权益.

2.2 系统初始化

设P={p1，p2，…，pn}是所有投标人的集合，并有访问结构A={A1，A2，…，Am}，其中Aj={p1，p2，…，p1}⊂A 是授权子集，1≤j≤m.

令G1为GDH 群，且其阶为一大素数q，P为G1的生成元.双线性映射e 表示为e:G1×G1→G2.设一个杂凑函数为H0:{0，1}*→G1，选择随机数s∈Z*q作为招投标管理机构和注册中心之间的共享密钥，并公布sP 的值作为招投标管理机构的公钥.另外，招投标管理机构和注册中心还共享一个秘密值x∈Z*q，注册中心随机选择k 和x，v1，v2，v3，…，vr∈K，其中v1=k，V=(v1，v2，v3，…，vr).

2.3 招标

招标人首先要制作招标文件，报招投标管理机构审批.审批后，招标人利用审批的文件到注册中心进行注册，获取USB 接口的电子钥匙，然后利用USB Key 登录到招投标管理网站，发布招标公告.

2.4 投标

(1)投标人pi∈Aj首先到注册中心进行认证，提交其身份信息ⅠDi.

(2)投标人pi随机选取bi∈Z*q，计算yi=biP，并公布yi.

(3)注册中心随机选取ai∈Z*q，分别计算:ri=aiP，hi=xH0(ⅠDi)，Ui=s(yi+ri+hi)=s(biP+aiP)+sxH0(ⅠDi).注册中心公布ri和hi，并将ri和Ui通过阈下通道发送给投标人pi.

(4)投标人pi制作好投标书Mi后，根据矢量空间秘密共享方案中的wi和投标人pi自己随机选择的bi，分别计算:Zi=H0(Mi)，di=(wi+bi)Zi，ti=di+Ui.这样，投标人pi就可以生成自己的签名(Ui，di，ri，hi，yi，ti，Zi，Mi，Ti)，其中Ti是投标人pi签名时间戳.同时，投标人pi公布自己的wiP 的值，并将自己签名中的(Ui，di，ri，hi，yi，ti，Zi，Ti)提至注册中心进行验证.

(5)注册中心收到投标人pi的签名(Ui，di，ri，hi，yi，ti，Zi，Ti)后，检查投标人pi是否有撤销时间戳.

i)若投标人pi没有撤销时间戳，则验证:

e(ti，P)=e(Zi，wiP)e(yi+ri+hi，sP)e(Zi，yi).

若等式成立，则说明签名有效.否则签名无效.

ii)若投标人pi有撤销时间戳，则先用撤销时间戳与签名时间戳Ti进行比对，如果撤销时间戳在签名时间戳前，则该签名无效.否则，验证:

e(ti，P)=e(Zi，wiP)e(yi+ri+hi，sP)e(Zi，yi).

若等式成立，则说明签名有效.否则签名仍无效.

此时，投标人pi签名中的时间戳经过验证通过后，注册中心根据投标人pi的签名生成一个签名有效时间戳T'i，然后将T'i发送给投标人pi.若验证没有通过，则所投标书作无效处理.

(6)投标人pi收到注册中心的签名时间戳T'i后，先验证时间戳T'i的合法性，然后将其与自己的签名连在一起，形成(Ui，di，ri，hi，yi，ti，Zi，Mi，Ti，T'i)，并将其发送至招投标管理机构.

(7)招投标管理机构收到投标人pi的签名(Ui，di，ri，hi，yi，ti，Zi，Mi，Ti，T'i)后，验证Zi=H0(Mi)，若成立，则说明Mi有效.然后再验证签名时间戳T'i和Ti的时效性.所有验证通过后，根据Mi生成相应的时间戳^Ti，并将其发送给投标人pi.

2.5 开标

投标时间一旦截止，便进入到开标阶段，招投标管理机构不再接收任何投标人投标书.然后，招投标管理机构分别计算:

由投标人子集Ai生成的群签名为:.

σ=((U1，U2，…U1)，(y1，y2，…，y1)，(r1，r2，…，r1)，d，Y，R，g，h，t，(M1，M2，…，M1)).

最后每个投标人pi以(Mi，H0(Mi)，σ)作为投标信息.招投标管理机构将(M1，M2，…，M1)放到网上评标系统中，并秘密保存好，以供评标专家评标使用.

2.6 评标

在电子招投标系统建立之初，就需要建立评标专家库.首先，评标专家向招投标管理机构申请，招投标管理机构审核通过后，将其录入到专家库中，同时将相关信息转交至注册中心.注册中心根据评标专家的个人信息进行注册并登记，生成个人的USB Key，以用来电子评标的身份验证.

当开标结束之后，招投标管理机构从评标专家库中随机抽取评标专家，并通知评标专家进行评标.评标专家接到通知后，利用自己的USB Key 通过安全网关SSL 来确认其身份，在规定的时间内上网登录电子评标系统，开始评标，确定中标的投标书Mx.

2.7 定标

评标专家评标结束后，招投标管理机构验证投标信息(Mx，H0(Mx)，σ)的正确性，计算:

若等式成立，该投标信息有效，然后将(Mx，H0(Mx)，σ)发送给注册中心.注册中心收到(Mx，H0(Mx)，σ)后，计算:

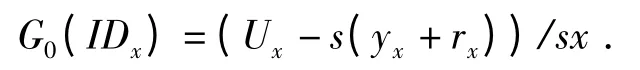
然后，打开该签名，与注册时提供的身份信息进行比对，找出中标人的信息，从而确定最终的中标人.若不成立，则投标信息(Mx，H0(Mx)，σ)无效.

3 方案的安全性及效能分析

3.1 安全性分析

(1)本方案是基于求解椭圆曲线的离散对数问题，攻击者在获得wiP 和kP 的值后，要想从中计算出wi和k，此时必须能求解其多项式算法，但对于椭圆曲线的离散对数来说，到目前为止尚未出现好的低于指数级时间的求解算法，即已知wi、k 和P，可方便计算出wiP 和kP，但其逆运算在计算上是不可解的.这样，攻击者也就无法计算出wi和k.

(2)所有参与本项目的投标人都可以对中标人的签名(Mx，H0(Mx)，σ)进行验证，计算e(tx，P)=e(Zx，kp+g)e(Y+R+h，sP)，从而保证在整个招投标过程中的公正性和公平性.

(3)只有通过注册中心验证的成员才能生成有效的群签名.注册中心为每个群成员pi分配一个子秘密wi.其身份可以在招投标项目完成后得到验证，计算e(tx，P)=e(Zx，kP+g)e(Y+R+h，sP).可以看出，只有经过授权的合法投标人才能正确的重构秘密k，任何来自非授权的投标人或攻击者都无法进入群内.这样，可以确保招投标过程的合法性.

(4)投标人pi在注册中心注册时，注册中心会对投标人的签名时间戳Ti进行验证，并对有效签名投标人pi发送时间戳T'i.同时，投标人pi在投标成功后，招投标管理机构也发送相应的时间戳^Ti.这样，不仅可以保证招投标过程中的时效性，同时还能实现招投标过程中投标书传输的不可否认性.

(5)招投标管理机构可以计算e(ti，P)=e(Zi，wiP)e(yi+ri+hi，sP)e(Zi，yi)，验证群签名的有效性，但不能从Ui=s(yi+ri+hi)得到投标书Mi与投标人pi的ⅠDi之间的联系，从而避免了招投标管理机构在招投标过程中泄露投标人的商业机密而产生的“商业贿赂”行为.

(6)伪造者无法伪造投标人pi的签名.假设伪造者随机选择，计算，公布=，从而来伪造投标人pi的签名，此时，在不知道k 和(wi+bi)的情况下，要想找到w'i，使得(w'i+b'i)H0(Mi)=(wi+bi)H0(Mi)，需要解决椭圆曲线的离散对数问题，这是一个到目前为止尚未能解决的数学难题.这样，伪造者就无法伪造投标人pi的签名.

(7)投标人pi将自己投标书中的签名(Ui，di，ri，hi，yi，ti，Zi，Ti)发送至注册中心验证，其中只发送了Zi，而没有发送Mi，这样即使注册中心将签名打开，将Zi与投标人pi的ⅠDi联系起来，但也无法具体知道投标人pi标书Mi的详细内容，从而避免了注册中心在招投标过程中泄露投标书的信息而产生的“商业贿赂”行为.

(8)授权投标人任意多个联合都不可能重构秘密向量V=(v1，v2，v3，…，vl).秘密向量V 可以根据授权投标人子集中的所有参与者所持有的wi来计算.同时授权投标者任意多个联合也不能通过Ui=s(yi+ri+hi)得到秘密s，x 以及H0(ⅠDi).这样就可以有效阻止在招投标过程各投标人之间的“串标”行为.

(9)本方案中涉及到秘密信息内容，都是通过阈下通道技术进行隐蔽性传输，避免网络攻击者的窃听和攻击，从而保证其传输的安全性.

3.2 效能分析

本电子招投标方案是在文献［3］的基础上进行改进和完善的，在计算量方面，本方案与文献［3］的比较如表1所示(其中ME 表示指数和多指数运算，BM 表示双线性对运算.)，从表中可以看出，本方案无论是在初始化阶段，还是在投标、评标以及定标阶段，在计算量上占有明显优势，其所耗计算工作量要比原方案小得多.在通信量方面，在相同的安全性要求下，本方案与文献［3］的比较如表2所示，从表中可以得出，本方案无论是在签名长度，还是在公钥、私钥长度方面，都有很大的改进，效率得到很大提高.

表1 计算量对比

表2 通信量对比

4 结语

本方案是在已有的群签名方案基础上进行了改进和完善，在满足电子招投标系统安全性的基础上，优化了系统的过程，提高了电子招投标系统的效率.分析表明该方案的安全性可以得到有效保障，其在实际使用中的招投标效率明显得到提高，整个招投标过程越发显示公开、公平、公正.本方案适用于分布式大规模的电子招投标，具有较高的使用价值.

［1］Liu Xin，Xu Qiu－liang，Shang Jiu－qing.Proceedings of the 3rd International Conference on Information Security［C］.New York:ACM，2004.

［2］BONEH D，BOYEN X，SHACHAM H.Lecture Notes in Computer Science［C］.Betlin:Springer－Verlag，2004.

［3］马春波，敖瑶，何大可.基于双线性映射的多重签名与群签名［J］.计算机学报，2005，28(9):1558－1563.

［4］李斌，丁勇.基于群签名的电子拍卖方案［J］.桂林电子科技大学学报，2011，31(2):151－154.

［5］赵丽萍，汤文亮.基于群签名的安全电子拍卖方案［J］.计算机仿真，2010，27(5):297－300.

［6］唐丽卫，杜伟章.一种基于双线性对的动态群签名方案［J］.长沙理工大学学报:自然科学版，2012，9(1):90－94.

［7］高天亮，夏清国，王玺.一个动态群签名的实用性分析［J］.科学技术与工程，2011，11(6):1222－1224.

［8］赵树平，王化群.群签名方案的安全性分析及其改进［J］.计算机工程与应用，2009，45(20):108－111.

［9］赵志华，张永新.基于网上招投标系统的安全性研究［J］.大庆师范学院学报，2010，30(3):31－34.

［10］张国俊，张建峰.电子签名技术在网上招投标系统中的应用［J］.常州信息职业技术学院学报，2011，10(4):22－25.