一类特殊指数和的均值估计

(琼州学院 数学系，海南 三亚572022)

0 引言

在文献［1］中，利用van der Corput 方法，可计算如下形式的指数和:

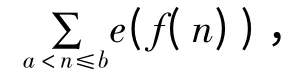
其中f(n)为一实值函数，且符号e(x)表示e2πix.诸如此类指数和，在数论课题的研究中，有着广泛的应用.本文主要研究当函数f(n)为一多项式函数时，此类指数和的均值估计.

假设d≥2 为一固定整数;a1，a2，…，ad为任意非零实数:γ1，γ2，…，γd为非整数的实常数:M，M1为满足条件5＜M＜M1≤2M 的实数.令

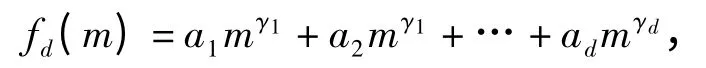
并令R=|a1|Mγ1+|a2|Mγ2…+|ad|Mγd.下面，我们来研究指数和

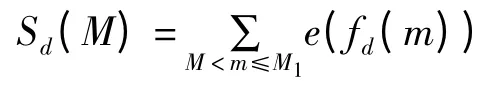
的估计式.

1 预备知识

本文需要用到如下引理:

引理1.1［2］设k≥2 为一固定整数，a1，a2，…，ak为非零的实数，α1，α2…，αk为非整数的实常数，Δ＞0.令Ⅰ表示［1，2］的一个子区间，使得

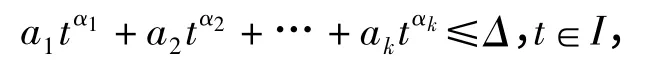
则有

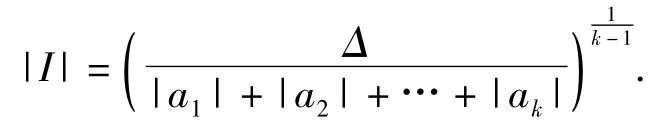
引理1.2［1］假设f(n)为定义在区间［N，N1］上的实值函数，其中2≤N＜N1≤2N.如果0＜λ3≤f(3)(x)≤αλ3，那么

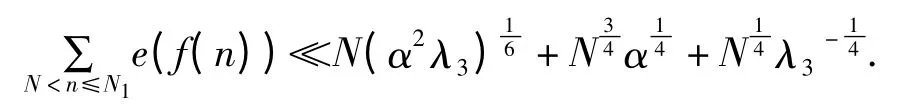
如果存在正常数c1，c2，使得c1M≤|f(j)(n)|≤c2M，j=1，2，3，4，5，6，那么

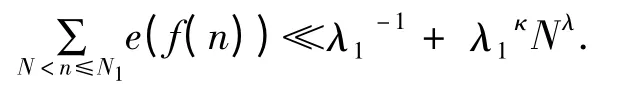
特别地，当λ1=1 时，有其中(κ，λ)为指数对.

引理1.3［2］假设z(n)为任意复数，1≤Q≤N，那么

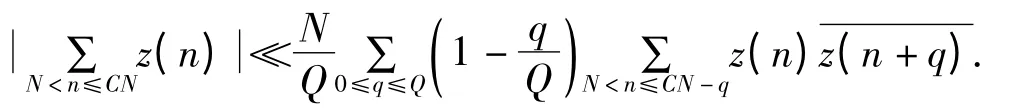
2 主要结果

证明:设δ＞0 为一待定参数，将区间［M，M1］划分为如下两部分:

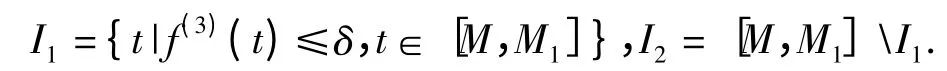
下面用引理1.1 和引理1.2 分别估计Sd(M)在Ⅰ1和Ⅰ2上的和.

若t∈Ⅰ1，则有

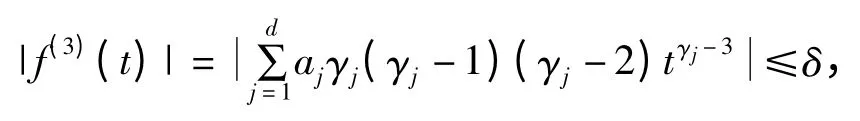
所以得到

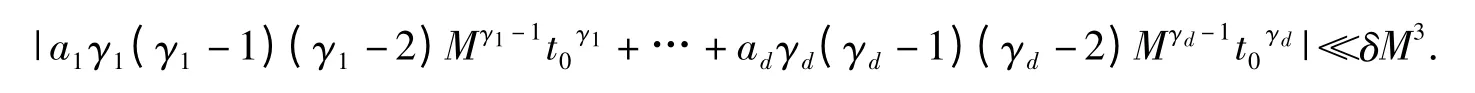
其中t0=，则t0∈［1，2］.

由引理1.1 有，满足上述不等式的［1，2］的子区间Ⅰ'1(t0∈Ⅰ'1)的长度为

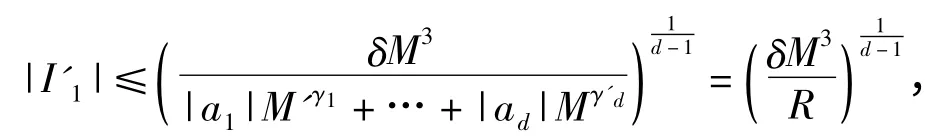
下面估计Sd(M)在Ⅰ2上的和:

令Ⅰ2j={t|2jδ＜|f(3)(t)|≤2j+1δ，t∈［M，M1］}，j≥0.则由引理1.2，得

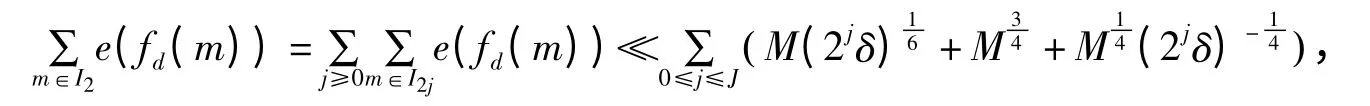
整理即得

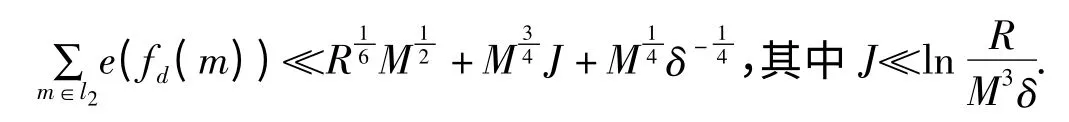
这样就得到了

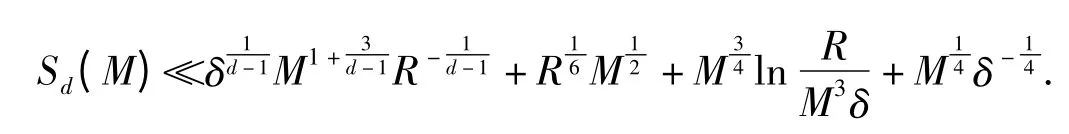
3 估计II 型指数和的应用

假设l≥2 为一固定的整数，γl(1＜γl＜…＜γ2＜γ1＜2)为实数，Y 为一足够大的数，δ=δ(γ1)＞0 为依赖于γ1的常数.利用上述定理2.1，可处理如下Ⅱ型指数和

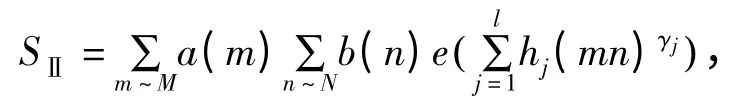
其中hj为满足条件1≤|hj|≤Yδ(j=1，2，…，l)的实数.设我们有

定理3.1 令0＜δ=δ(γ1)＜1，且a(m)，b(n)为复数，使得

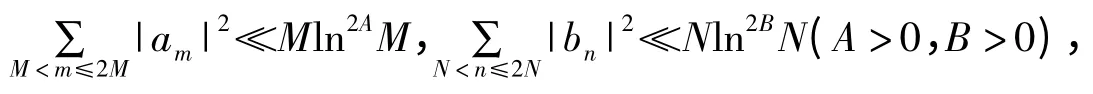
那么，对于Y2δN≪Y1/2≪MN≪Y，则有

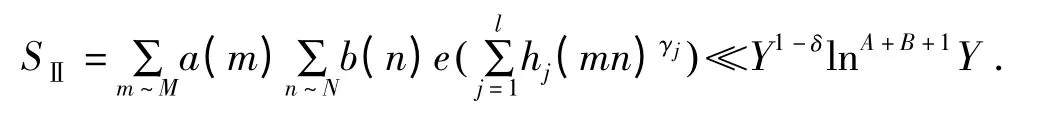
证明 取Q=［Y2δln－1Y］，那么Q=o(N).由柯西不等式和引理1.3，得

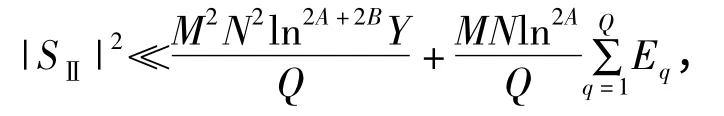
其中

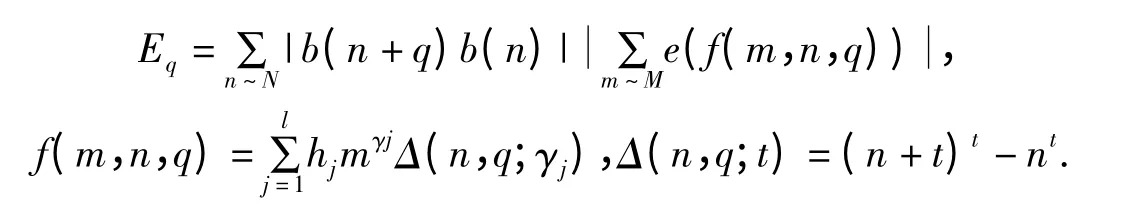
从而由定理2.1 得

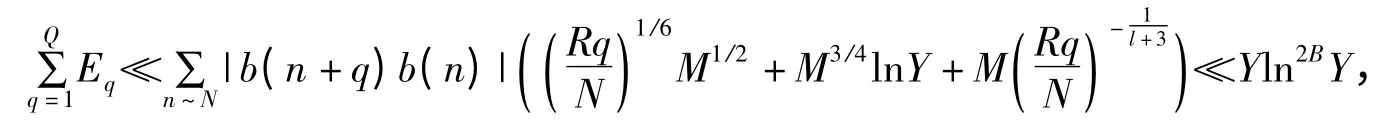
即定理3.1 成立.

［1］S.W.Graham，G.Kolesnik.Van der Corput＇s Method of Exponential Sums［M］.Cambridge University Press，1991:22－41.

［2］Zhai Wenguang.On the k－dimentional Piatetski－Shapiro prime number theorem ［J］.Sci.in China:Ser.A，1999，29:797－806.

［3］张天平.关于数论中一些著名和式的均值研究［D］.西安:西北大学，2008.