杆轴向振动挤出成型装置的设计及振动特性仿真*

吴上生 胡安涛 杜锦

(1.华南理工大学 机械与汽车工程学院，广东 广州510640;2.中国兵器装备集团公司861 厂，湖南 长沙410100)

传统挤出成型设备的改进和发展主要集中于对螺杆结构的深入研究和不断改进.通过增加螺杆长径比或改进螺杆的结构，以提高物料的混炼效果［1］，最终达到提高制品质量的目的.这样的设计往往使设备体积增大，料筒和螺杆间的摩擦、磨损加剧设备噪声增大，使用寿命大大缩短［2-4］;同时螺杆加工难度增大，往往难以达到预期要求.现代振动技术的发展，使得将振动力场引入挤出成型加工过程成为可能.前人对挤出机局部施加振动［5-6］，创造性地改善了挤出特性，显著提高了挤出制品的质量.与传统非振动挤出成型方式相比，振动式挤出设备的制造成本、能耗降低近50%，噪声更低，对物料适应性更好，塑化温度低，冷却时间短，制品质量显著提高［7-9］.

当前使用的振动挤出机主要采用电磁动态激振的方式，使螺杆产生轴向振动，这种激振装置结构较为复杂，且振动可靠性、稳定性有待提高［10］.文中提出一种新型机械振动式挤出成型装置，采用机械滚子轴向激振的方式［11］，实现了挤出螺杆轴向周期性振动，较明显地简化了螺杆轴向激振装置的结构;同时应用ADAMS 虚拟样机仿真技术对螺杆振动输出波形进行仿真试验，对该机械式激振方式的可靠性、稳定性进行验证，并对该新型轴向振动挤出成型装置的可行性及有效性进行验证.

1 振动挤出成型装置的工作原理

机械式振动挤出成型装置主要结构如图1所示.激振式半联轴器10 作为激振和振动输出的核心部件，其底面周向分布着光滑过渡的凹凸激振曲面.激振式半联轴器与主动轴1 之间通过滚动花键11连接，确保两者同步转动时，可实现轴向相对运动.

滚子限位盘7 与箱体6 固定连接，其中心带孔，通过滚子轴承18 与主动轴1 连接.各激振滚子8 镶嵌安装在滚子限位盘7 底面周向均匀分布的半圆锥形滚子槽中，并用滚子保持架9 将滚子轴向定位，防止其从滚子槽中脱落;各滚子在滚子槽中可自由滚动.激振式半联轴器10 和普通半联轴器12 通过螺栓固定连接;普通半联轴器12 和螺杆17 通过花键连接;主动轴1 和螺杆17 连接联轴器的轴端通过轴端挡圈分别与两个半联轴器固定，使得激振式半联轴器、普通半联轴器和螺杆成为一体，同时转动，同时轴向振动.应特别注意的是，激振式半联轴器和轴端挡圈之间要预留一段大于A(A 为轴向振幅)的轴向间隙.

图1 螺杆振动挤出成型装置核心结构Fig.1 Core structure of extrusion equipment with screw vibration

初始状态下，安装于滚子槽中的激振滚子和激振式半联轴器底面的凹凸激振曲面在最低点啮合.传动齿轮2 将转矩输入主动轴，并带动激振式半联轴器同步转动.激振式半联轴器底面的凹凸激振曲面与各激振滚子之间产生啮合接触运动.转动力矩施加在激振曲面，并转化为接触力作用在滚子上，滚子对激振曲面产生大小相等的反作用力.此反作用力轴向分力即为驱动螺杆轴向振动的激振力.当滚子与凹凸激振面最低点啮合时，螺杆达到其振动幅值的最小值点，当滚子与凹凸激振曲面最高点啮合时，螺杆达到其振动幅值的最大值点［11］.

该振动挤出成型装置的螺杆在振动工作中，熔融物对螺杆产生的背压，可保证滚子和凹凸激振曲面始终接触啮合.但在设备启动初期、尚未加工的空载阶段，由于未产生背压，激振曲面相对于滚子易产生惯性腾跳，因此在料筒的法兰连接端与螺杆之间设置预紧弹簧，通过弹簧预紧压缩产生的轴向力使空载阶段的滚子和曲面保持良好接触啮合.

2 凹凸激振曲面的设计

2.1 振动规律的确定及二维激振轮廓曲线方程的推导

滚子和激振曲面接触运动的简化模型如图2所示.图中，半径为R 的基圆柱面与凹凸激振曲面相交，其相交截面上的激振曲线与滚子圆截面啮合.

图2 滚子与激振曲面啮合原理Fig.2 Meshing principle of the rollers and vibration surface

若假设激振曲面固定不动，而滚子随轴旋转，则滚子将沿着凹凸激振曲面周向滚动，滚子始终与激振曲面相切.根据单参数包络理论［12］可知，激振曲线为滚子面圆簇的包络线.据此，采用凸轮设计的“反转”思想及经典包络理论求解凹凸激振曲面的数学模型.将半径为R 的环形激振曲线展开投影在XY 坐标平面内，并以一个滚子沿凹凸激振曲线啮合滚动进行研究，如图3所示.

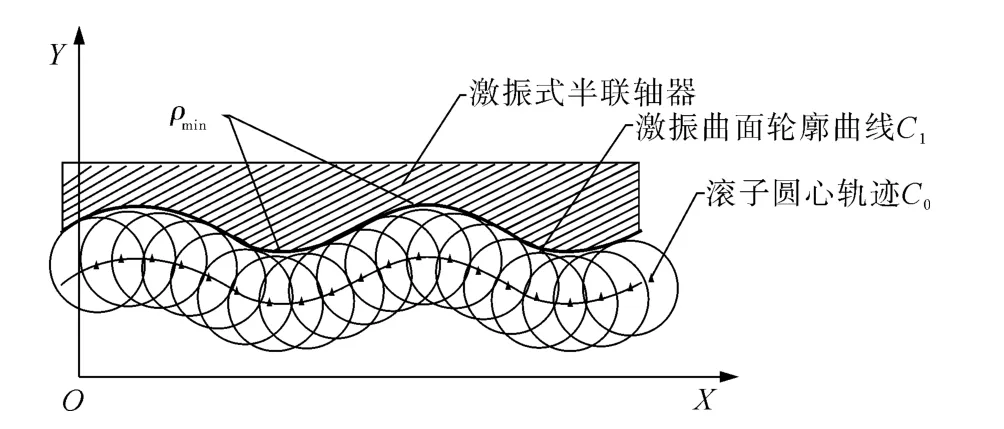
图3 半径为R 的激振横截面展开图Fig.3 Expanded view of intersecting surface of vibration surface at radius R

滚子圆心轨迹曲线C0即为滚子沿激振面滚动时的振动轨迹线.为了避免滚子和激振曲面接触运动过程中产生冲击和应力集中、突变，同时尽可能减小滚子和滚面的摩擦磨损，拟定振动规律为简谐振动，即假设C0轨迹曲线方程为

其中:S0为滚子中心振动位移;A 为振幅;λ 为比例系数;h 为半径为R 的基圆柱面与凹凸激振曲面相交所得的激振曲线弧长，亦即图3中滚子截面圆心轨迹沿X 轴的位移;为研究方便，假设振动初相位η0= 0，则简化后C0曲线方程为

由式(2)得

由式(3)-(4)可知，由式(2)决定的简谐运动规律，其速度和加速度均为连续的简谐运动，不会出现冲击和应力突变，运动平稳可靠.因而拟定以式(2)作为本研究的振动位移方程.

如图2，设激振曲面在半径为R 的截面处激振滚子截面半径为r，则由式(2)和半径r 的圆决定的圆簇曲线方程为

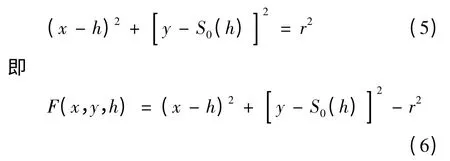
结合式(2)、(6)可得

根据经典包络理论［12-13］，可得图3激振曲面轮廓曲线C1的方程为

联立式(6)-(8)并化简求得图3中曲线C1的参数方程为

式(9)即是半径为R 的激振曲面横截面的展开轮廓曲线方程，即二维激振轮廓曲线C1的方程.

2.2 三维凹凸激振曲面方程的导出

为了将二维激振轮廓曲线C1映射为图2所示的空间环形凹凸激振曲面，作如下映射参数定义:

h—半径为R 的基圆柱面与凹凸激振曲面相交所得的激振曲线弧长，若激振面转动角度为θ，则满足:

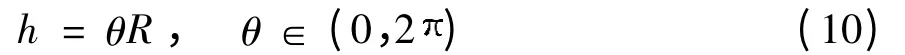
n—与激振曲面同时啮合的滚子数目，满足

β—激振滚子圆锥角，

由图2可知:

据式(2)、(10)-(11)将振动曲线C1环向映射后得激振曲面轴向振动位移方程为

据式(9)-(13)进行参数替换，并进行空间代换，将式(9)映射到三维空间，得到图2所示的激振曲面参数方程为

2.3 边界条件

为了避免滚子和激振曲线接触运动中出现“卡死”现象，图3中曲线C0的最小曲率半径ρmin满足

滚子圆心轨迹曲线C0的曲率半径为

联立式(2)、(10)-(13)、(16)-(17)并化简可得激振曲面最小基圆柱面半径Rf满足如下关系:

如果半径R 小于Rmin，滚子在激振曲面的最高点和最低点无法正常滚动，出现“卡死”或打滑现象.

3 激振面和螺杆的几何参数确定及建模

根据式(15)、(18)，选择合适的几何参数(见表1)，即可设计符合振动要求(式(14))的激振曲面，如图4所示.根据螺杆直径标准，计算出符合要求的螺杆结构参数，如表2所示.运用三维建模软件即可设计出如图5所示的螺杆结构，进而设计如图1所示的振动挤出机核心部件.

表1 凹凸激振曲面主要几何参数1)Table1 Main geometric parameters of the undulant vibration surface

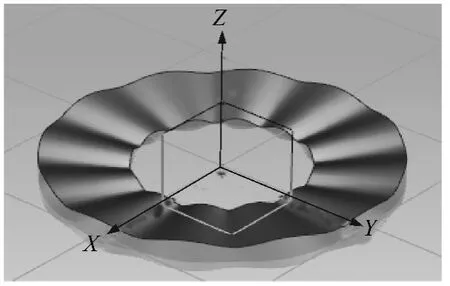
图4 凹凸激振曲面三维模型图Fig.4 3D model of the undulant vibration surface

表2 螺杆计量段三维模型结构参数Table2 3D structural parameters of metering section of the screw

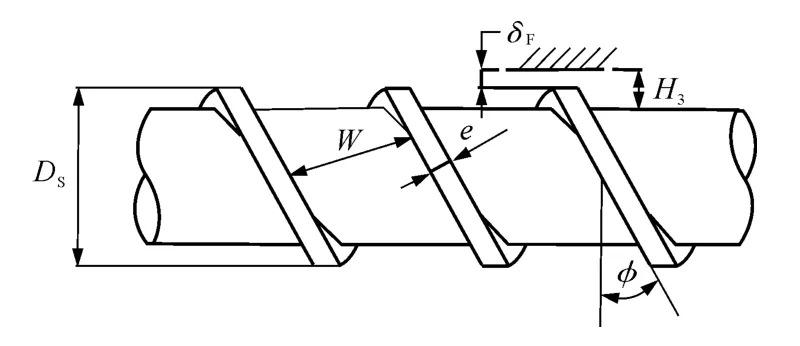
图5 螺杆计量段简化模型Fig.5 Simplified model of metering section of the screw

4 螺杆振动物理模型建立及参数确定

4.1 动力学模型的建立

新型滚子激振式振动挤出成型装置的振动结构主要由激振式半联轴器、普通半联轴器、螺杆等回转部件组成.为了研究方便，作如下几点假设［14-15］:将具有相同振动规律的激振式半联轴器、普通半联轴器和螺杆及其辅助部件当作有机整体，命名为广义螺杆，并用一个集中质量块代替;螺杆为刚性体，不会发生变形;将聚合物固体对刚性螺杆的摩擦阻尼和熔融物对螺杆的粘滞阻尼统一折算为等效粘性阻尼c;忽略预紧弹簧的质量和阻尼作用.

根据图1的螺杆振动工作原理和图2所示的啮合振动机理，结合以上的基本假设，可建立螺杆振动力学模型，如图6所示.其中，k 为预紧弹簧刚度，m为广义螺杆质量，c 为聚合物等效粘性阻尼系数，FT为由于施加到凹凸激振曲面上的扭矩T 而产生的滚子对凹凸激振曲面的等量反作用力，FTz为FT的轴向分力，(亦为激振力)，FTt为FT的切向分力，Fz为挤出成型过程中螺杆受到的轴向力，x(t)为螺杆轴向振动位移，v 表示激振式半联轴器切向线速度.

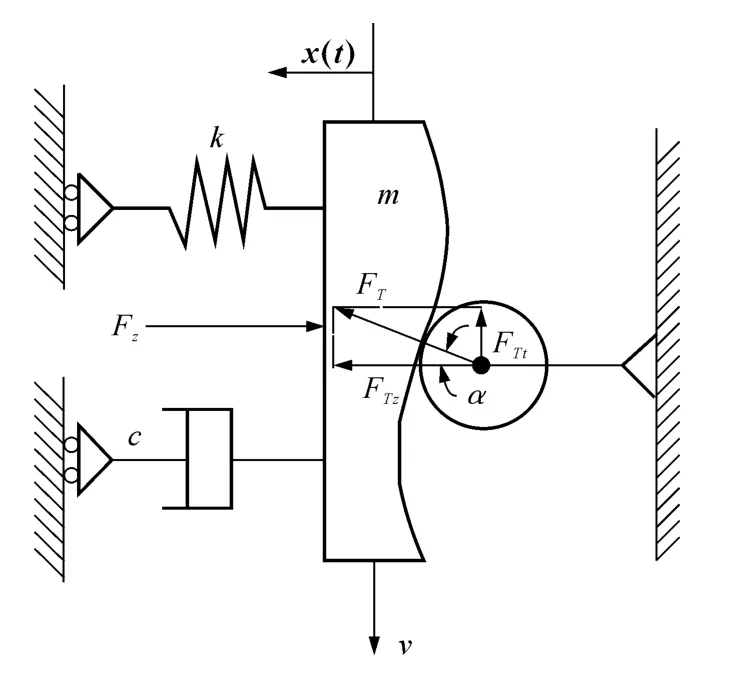
图6 螺杆振动力学模型Fig.6 Vibration mechanical model of the screw

4.2 数学模型的建立及关键参数的确定

根据图6的振动力学模型可得螺杆稳定振动时的振动数学模型:

(1)滚子抗扭矩反作用力FTz

设激振式半联轴器输入功率为P(kW)，主动轴转速为N(r/min)，则激振式半联轴器输入扭矩为

图6中的压力角α 可根据图3中曲线C0及式(2)得到:

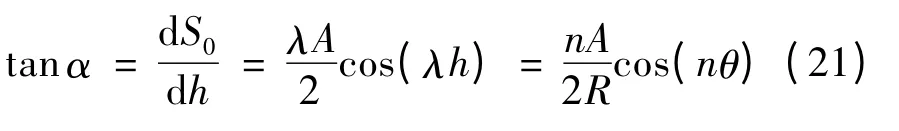
则

(2)熔融体挤出成型加工时螺杆受到的轴向力

在熔融体挤出成型加工时，螺杆受到的轴向力包括两部分:机头处熔融物对螺杆头部端面产生的背压力以及由于动载荷产生的附加轴向力，一般可用如下公式计算［16］:

其中:θb为机筒内表面处螺纹升角;为螺杆平均直径处螺纹升角;N 为螺杆转速，亦即主动轴转速;η为熔融物黏度;L3为计量段长度;H3为计量段螺纹根部至机筒内表面的距离.

(3)等效粘性阻尼系数c

由于加料段的固体颗粒、固体床对螺杆产生的摩擦力较复杂，为了简化分析，将加料段和熔融段聚合物对螺杆的阻尼统一折算为计量段熔体对螺杆的等效粘性阻尼［17］，即

其中，Kc为通过实验测定的折算系数，c3为计量段的粘性阻尼系数.

据螺杆计量段结构参数，计量段的粘性阻尼系数［18］为

其中，μ 为聚合物熔体的内摩擦系数，i 为螺杆螺纹头数，此处i=1.则

(4)预紧弹簧刚度k 的计算

对于圆柱形密圈螺旋弹簧，其刚度可采用材料力学公式计算:

其中，G 为弹簧材料切变模量，d 为弹簧丝直径，D为弹簧直径，nk为弹簧的有效圈数.

(5)弹簧初始压缩预紧长度l0

当设备空载启动时，由于螺杆未受到熔融物产生的背压，振动机构振动过程中，激振曲面相对于滚子易产生惯性腾跳而相互脱离，影响振动的稳定性.因此通过预紧弹簧压缩一定的长度l0产生的预紧轴向力使空载阶段的滚子和曲面保持良好啮合.

空载振动阶段，聚合物对螺杆的等效粘性阻力为0，同时螺杆受到的轴向力Fz也为0，据此将式(19)进行简化，得到空载启动时的振动数学模型:

本振动系统连续振动方程为

其中，ω 为主动轴角速度.

将式(29)代入式(28)并进行化简可得

为了保证滚子和凹凸激振曲面不发生相互脱离，需满足

将式(32)代入式(31)并化简，可得弹簧初始预紧长度l0需满足

5 螺杆轴向振动性能动力学仿真分析

5.1 振动仿真模型建立

将UG 建立的螺杆振动挤出装置的三维模型通过适当的格式转换，导入刚体动力学分析软件ADAMS 中.为了简化分析，在ADAMS 仿真环境下，将料筒、箱体、支座、底座等固定不动的部件用仿真软件中的“ground”这一虚拟部件等效替代.将聚合物对螺杆的等效粘性阻尼用预紧弹簧对振动螺杆的阻尼代替，此预紧弹簧可用ADAMS 中的虚拟弹簧表示.同时添加必要的运动约束、载荷、接触及驱动，使仿真模型符合规定的各项技术要求.所建立的螺杆轴向振动挤出装置的仿真模型如图7所示.

图7 轴向振动挤出装置仿真模型Fig.7 Simulation model of the axial vibration extrusion equipment

5.2 螺杆轴向振动仿真及结果分析

文中以低密度聚乙烯LDPE 为样本，利用式(23)、(26)计算聚合物对螺杆的阻尼作用及聚合物熔体对螺杆的轴向力，进而设定振动仿真主要参数，如表3所示.仿真结构如图8所示.

表3 单螺杆轴向振动仿真参数Table3 Axial vibration simulation parameters of the single screw

由图8(a)、8(b)可知，该振动挤出成型装置的振动位移和振动速度波形与理论计算预期(式(2)-(3))高度吻合，严格遵循简谐振动规律;只有图8(c)加速度波形存在一定的波形失真，但失真度较小，整体上仍符合简谐振动规律.

螺杆振动轴向位移频谱、轴向速度频谱、轴向加速度频谱如图9所示.

由图9可知，在凹凸激振曲面几何参数确定的情况下，螺杆轴向振动频率只与主动轴转速有关，而与其他条件无关.在实际运用中，通过调节电机转速就可以控制螺杆轴向振动的频率，方便可靠，避免了多变量影响而造成频率调节不准确的问题.

由图9(a)、9(b)的频谱图可知，在17 ～100Hz 范围内，谱线幅值几乎为0，说明在振动位移和振动速度基波上几乎没有叠加高次谐波，因而其振动波形几乎不存在波形失真.而对于图9(c)，在17 ～100 Hz 频率范围内，谱线在0 值上方小幅波动，即在高频段存在大量的随机波.因而造成图8(c)所示的加速度振动波形失真.这种现象不难理解，在实际中，由于振动机构的滚子和激振面的非线性接触以及机械零部件之间的冲击，其受力状况不仅复杂，而且存在一定的随机性.因此，在振动加速度基波上，往往叠加高次谐波和随机波，振动加速度波形不可能输出理想的正弦波形［19-20］.

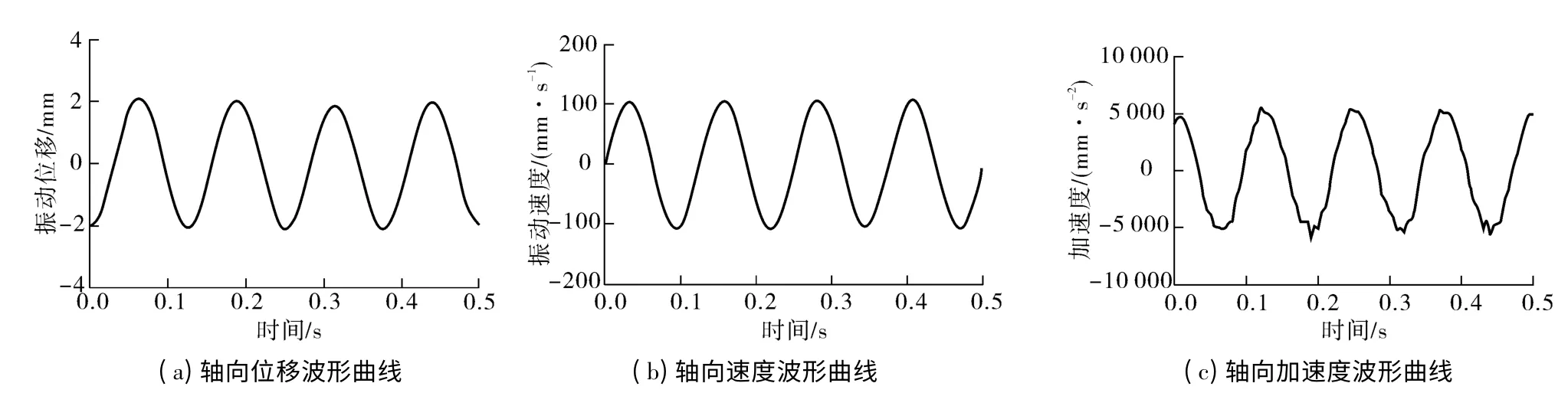
图8 螺杆振动轴向位移、轴向速度及轴向加速度波形曲线Fig.8 Axial displacement，axial velocity and axial acceleration curves of the vibration screw

图9 螺杆振动轴向位移、轴向速度及轴向加速度频谱Fig.9 Frequency spectrums of axial displacement，axial velocity and axial acceleration of the screw

综上对仿真结果的分析，该振动挤出成型设备的轴向振动特性基本达到了预期设计要求.

6 结语

文中提出了一种新型的振动挤出成型装置，分析了螺杆轴向振动工作原理，通过规定的正弦简谐振动方程，导出了凹凸激振曲面的数学方程，并建立了装置的核心结构模型;结合振动工作原理及受力分析，建立了螺杆振动力学模型及数学模型，并对各关键参数进行了理论推导求解;基于所建立的振动成型装置的三维模型以及所建立的力学模型，运用ADAMS 刚体动力学仿真软件对振动挤出成型装置的螺杆振动特性进行仿真实验，并得到了螺杆振动的位移、速度和加速度波形曲线以及频率特性曲线;通过对仿真输出波形及频谱的分析，证明了振动挤出装置虚拟样机的螺杆振动特性较好地符合预期目标，螺杆轴向振动特性较为稳定，基于相关假设，并施加仿真工作载荷、约束条件后，其振动位移曲线、速度曲线与理论分析较为吻合，加速度曲线存在一定的非线性失真，但属于正常现象［19-20］，文中还通过仿真实验证明了该新型的振动挤出成型装置的理论可行性及有效性，为聚合物挤出加工领域新设备的开发提供了一种理论技术支撑.

［1］Sakharov A S，Kolosov A E，Sivetskii V I，et al.Modeling of polymer melting processes in screw extruder channels［J］.Chemical and Petroleum Engineering，2013，49(5/6):357-363.

［2］瞿金平.聚合物塑化挤出新概念［J］.华南理工大学学报:自然科学版，1992，20(4):1-8.Qu Jin-ping.New concept of plasticizing extrusion of polymer［J］.Journal of South China University of Technology:Natural Science Edition，1992，20(4):1-8.

［3］Khametova M G.Analysis of steady non-isothermal flow of polymer melts in a single-screw extruder ［J］.Chemical and Petroleum Engineering，2012，48(7/8):488-493.

［4］Deng J，Li K，Jones H E，et al.Energy monitoring and quality control of a single-screw extruder ［J］.Applied Energy，2014，113:1775-1785.

［5］Ibar J P.Control of polymer properties by melt vibration technology［J］.Polymer Engineering and Science，1998，38(1):1-20.

［6］Casulli J，Clermont J R.The oscillating die:a useful concept in polymer extrusion［J］.Polymer Engineering and Science，1990，30(23):1551-1556

［7］胡汉杰.塑料挤出成型方法及设备研究取得重大突破［J］.中国科学基金，1997(3):75.Hu Han-jie.Extrusion molding method of plastics and the breakthrough of equipment research［J］.Science Fund of China，1997(3):75.

［8］Qu J P，Zeng G S，Feng Y H.，et al.Effect of screw axial vibration on polymer melting process in single screw extruders［J］.Journal of Applied Polymer Science，2006，100(5):3860-3876.

［9］付莉红，王中武，严山明.振动挤出对聚烯烃流变行为的影响［J］.塑料科技，2013，41(2):41-43.Fu Li-long，Wang Zhong-wu，Yan Shan-ming.The influence of vibration extrusion on the rheological behavior of the polyolefin ［J］.Plastics Science and Technology，2013，41(2):41-43.

［10］周南桥.电磁动态塑化挤出机成型机理、性能及展望［J］.中国塑料，1997，11(1):83-88.Zhou Nan-qiao.Forming mechanism，performance and prospects of the electromagnetic dynamic extruder［J］.Journal of China Plastics，1997，11(1):83-88.

［11］吴上生，陆振威，胡安涛.轴向推力旋转滚子激振式机械振动装置:中国，201310064147.2 ［P］.2013-02-28.

［12］常宗瑜，张策，杨玉虎.用包络理论生成空间分度凸轮的啮合曲面［J］.机械设计，2000(2):10-11.Chang Zong-yu，Zhang Ce，Yang Yu-hu.Generation of the meshing surface of spatial indexing cam according to the envelope theory［J］.Machine Design，2000(2):10-11.

［13］Churchill F T，Hansen R S.Theory of envelopes provides new cam design equation ［J］.Prod Eng，1962(35):45-55.

［14］阎胜文，瞿金平.单螺杆振动塑化挤出机螺杆转动对其轴向振动的影响［J］.中国机械工程，2006(9):941-945.Yan Sheng-wen，Qu Jin-ping.The influence of rotation on the axial vibration of single screw extruder in vibration［J］.China Mechanical Engineering，2006(9):941-945.

［15］瞿金平，王松若，阎胜文，电磁动态挤出机转动与轴向振动之间特性关系研究［J］.机械设计与制造，2009(1):141-143 .Qu Jin-ping，Wang Song-ruo，Yan Sheng-wen.Research of relationship between rotation and axial vibration of the electroma-gnetic dynamic extruder［J］.Machinery Design and Manufacture，2009(1):141-143 .

［16］张晋茂，杨兆福，陈锋，等.塑料机械设计［M］.2 版.北京:中国轻工业出版社，1995.

［17］瞿金平.聚合物动态塑化成型加工理论与技术(下卷)［M］.北京:科学出版社，2005.

［18］韦建召，瞿金平.电磁动态塑化挤出机螺杆振动系统聚合物阻尼分析［J］.噪声与振动控制，2004(4):39-41.Wei Jian-zhao，Qu Jin-ping.Polymer damping analysis for screw vibration system of the electromagnetic dynamic extruder［J］.Noise and Vibration Control，2004(4):39-41.

［19］杨少明.机械振动台的技术要求及其检定［J］.航空标准化与质量，1978(4):25-29.Yang Shao-ming.Technical requirements and verifycation of the mechanical vibration table ［J］.Aviation Standardization and Quality，1978(4):25-29.

［20］宋琼，朱长春，牛宝良.液压振动台建模与加速度波形失真分析［J］.机床与液压，2008，36(12):81-83.Song Qiong，Zhu Chang-chun，Niu Bao-liang.Modeling of hydraulic vibration table and analysis of the acceleration waveform distortion ［J］.Machine Tool ＆ Hydraulics，2008，36(12):81-83.