全局优化算法在船舶结构优化设计中的应用
2015-12-19冯新伟毕长飞
冯新伟,毕长飞
(1.辽宁水利职业学院,辽宁 沈阳110122;2.辽宁地质工程职业学院机电系,辽宁 丹东118008)
0 引 言
在船舶结构中存在着大量的龙骨结构,该类结构主要用于船身架构。龙骨结构主要由蒙皮与筋板构成,能够以较小厚度的钢板焊接得到刚度较大的钢结构,能够有效节约材料使用量。因此,这类结构得到较多关注。
近年来,部分学者对龙骨结构力学性能展开了广泛研究。姚谦峰等[1]为了研究龙骨结构承载破坏特性,建立了龙骨墙体结构并对其进行疲劳破坏试验,其中疲劳寿命试验采用低周载荷。通过研究,得出结构破坏规律以及结构破坏过程的钢结构应变规律计算公式,这为龙骨结构强度设计提供了有力参考。左宏亮等[2]为了研究龙骨结构开孔对结构屈曲模态振型、结构应力幅值、承载能力的影响,采用Ansys 软件建立龙骨结构有限元模型,研究了龙骨结构在轴向压力、横向弯矩以及压力弯矩作用下的结构响应特性。结果表明,龙骨结构的开孔会使其承载能力降低,然而应变幅值会有所降低,这对提高结构疲劳寿命十分有利。王昭俊等[3]对龙骨结构热传递性能进行研究,将龙骨结构边缘宽度、龙骨筋板厚度、龙骨筋板高度以及筋板之间距离作为设计因素,采用热力学分析软件对其热传递与热桥问题进行模拟计算。最终得出各结构参数对传热参数的影响。
现有文献对龙骨结构的研究较为广泛,主要集中于结构承载能力、传热性能方面的研究。龙骨结构在设计时,通常采用相同的筋板高度,在一定程度上这样的设计并不合理。因为龙骨跨度较大,其各个部位载荷并不相同。因此在不同部位采用不同的筋板高度能够使结构设计更加合理,受力更为均匀,也有利于节约材料。
针对该问题,本文提出一种基于全局优化算法的筋板高度优化方法。该方法以有限元模型为基础,采用Hypermesh 有限元前处理程序的MORPH 功能定义结构形状变量,具体优化流程如下:
1)建立龙骨结构几何模型。
2)采用Hypermesh 软件建立龙骨结构有限元模型。
3)采用MORPH 工具对筋板高度定义形状变量,并将其作为设计变量。
4)采用全局优化算法对模型进行优化搜索,函数响应值通过有限元过程返回。
2 全局优化算法
全局优化算法是一种常用的非线性优化搜索技术,其主要优点为全局收敛性好,有利于找到优化问题中的全局最优解。耿瑞光等[4]为了解决局部优化的缺陷,将全局优化算法应用于船舶轴系结构优化,将多提系统动力学和有限元方法相结合,建立波浪激励- 船- 轴系相互作用的结构优化模型,并对其进行优化设计,得到了令人满意的结果。陈龙等[5]为了提高车辆系统的平顺性,建立了车辆5 自由度动力学模型,将悬架刚度与阻尼作为优化设计变量,采用全局优化算法对其进行优化设计,结果表明:优化后的结构能使车辆系统在不同的车速下均获得较好的平顺性,乘员舒适性显著改善。
通常,全局优化数学模型可以表述为[6]:

其中,设计变量:

其中,n 为设计变量维数,则设计区域为:
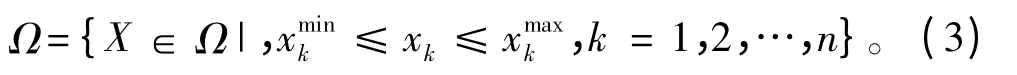
则个体质量mi对应的凸函数为:
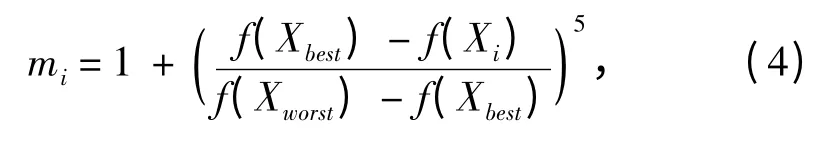
个体质量mi对应的线性函数为:
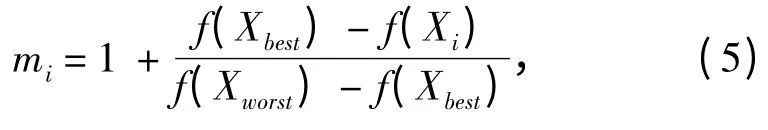
个体质量mi对应的凹函数为:
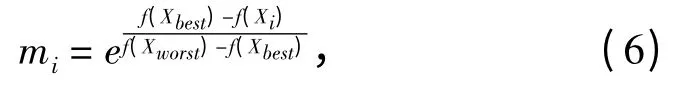
其中,Xbest为最适应个体适应参数:
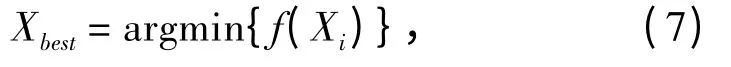
Xworst为最适应个体适应参数:
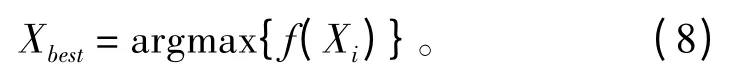
为了使其具有全局优化能力的同时能够具有一定的局部搜索能力,可以引入个体作用力函数:
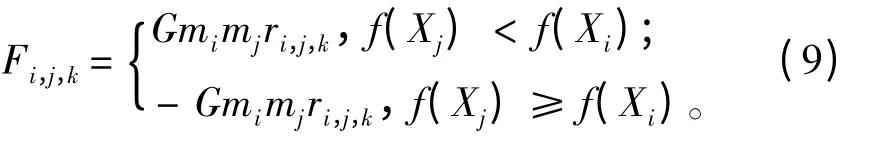
其中,ri,j,k为个体i、j 之间的距离;k 为距离所在维数,其计算公式为:
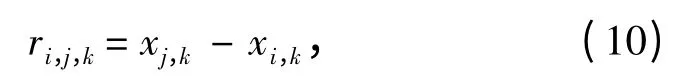
则所有个体合力可以表示为:
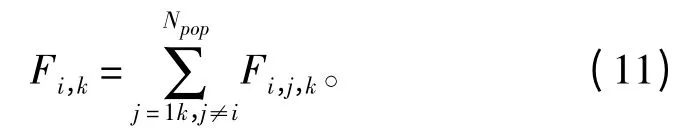
每个个体迭代优化过程采用如下迭代格式进行控制,速度进化为:
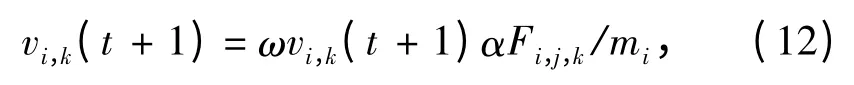
位移进化公式为:
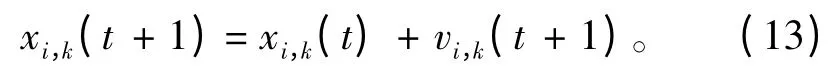
最终,全局优化算法为:
1)种群随机化。为各变量个体随机选择初始值,并对其计算适应值。并将进化代数置为0。
2)根据式(9)计算各个体之间作用力。
3)根据式(11)计算个体合力。
4)由式(4)~式(6)计算个体质量。
5)根据速度进化式(12)获得下一代速度值。
6)根据位移进化式(13)获得下一代位移值。
7)计算个体适应值大小,并对原种群中个体适应值参数进行更新。
8)重复上述过程,每重复一次,进化代数加1,直至达到收敛结果,则停止优化计算,并输出最优结果。
3 优化算例
船舶龙骨结构如图1 所示,主要由表面蒙皮与筋板组成。结构在受力过程中筋板应力分布极不均匀,为了使筋板结构设计更为合理,可以采用不等高度的筋板进行焊接,使结构中应力较大的部位具有较大的筋高度,提高其抗弯能力。在结构应力较小的部位采用较小的筋高度,这样不仅能够改善龙骨结构受力特性,还能有效提高材料利用率,节约材料。
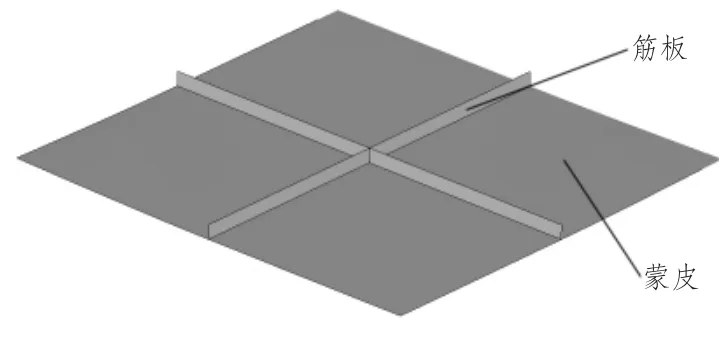
图1 龙骨结构简图Fig.1 Keel structure diagram
采用UG 软件建立龙骨几何模型,并采用先进的有限元前处理程序Hypermesh 对其进行离散处理。网格划分时,单元均采用四节点壳单元实现。壳单元厚度均取值为10 mm,本文选取的材料为45 号优质碳素钢,其弹性模型为210 Gpa,材料密度为7 800 kg/m3,泊松比为0.26。
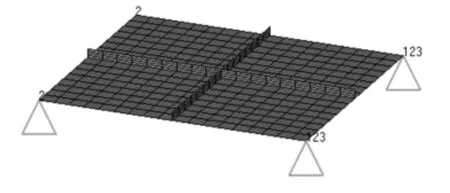
图2 有限元模型Fig.2 Finite element model
模型约束边界条件如图2 所示,龙骨结构在右端两转角处的节点被约束x,y,z 轴方向的位移自由度,分别采用数字1,2,3 表示。为了模拟船身在波浪航行过程中受到的波浪力,在其左端上方节点处加载一波浪时域载荷。
由于龙骨为一跨度较大的结构,为了简化问题,本文只建立部分龙骨结构有限元模型,其延展边界条件如图3 所示,其中左端下方节点约束y 轴方向位移自由度,此时结构变形特性与真实变形边界条件较为一致。因此,本文采用的该边界条件合理,能够反映龙骨全局结构特性。
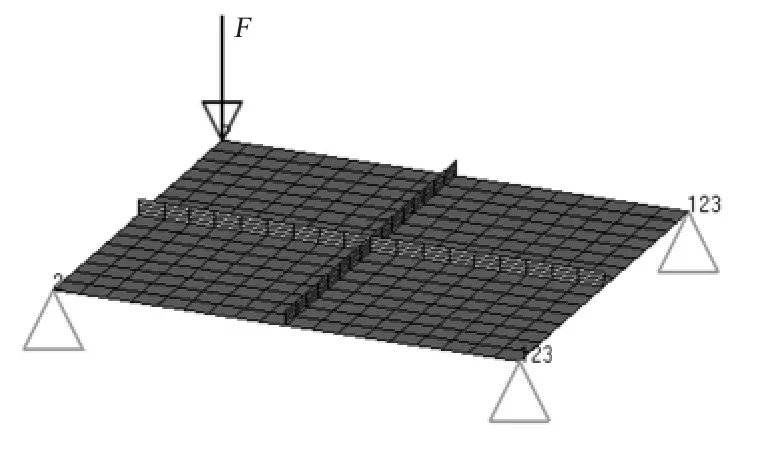
图3 载荷边界条件Fig.3 Loading boundary
在该优化中,龙骨结构的筋板高度将作为设计变量。为此,本文借助Hypermesh 软件的MORPH功能对筋板结构进行变形,并将变形前后节点位移矢量作为设计变量进行优化。
在形状变量1 中,纵向筋板与横向筋板相交的位置位移最大,并向四周逐渐线性减少(见图4)。
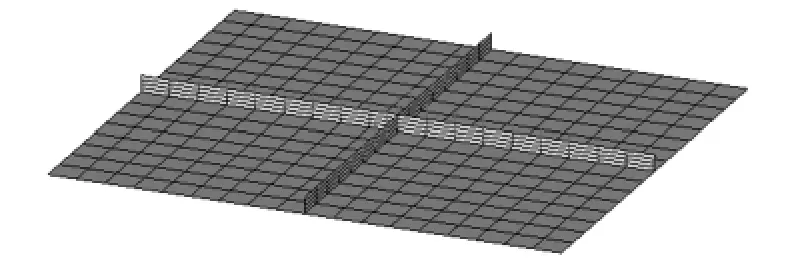
图4 形状变量1Fig.4 Shape design variable 1
在形状变量2 中,纵向筋板与横向筋板变形一致,向四周无递减(见图5)。
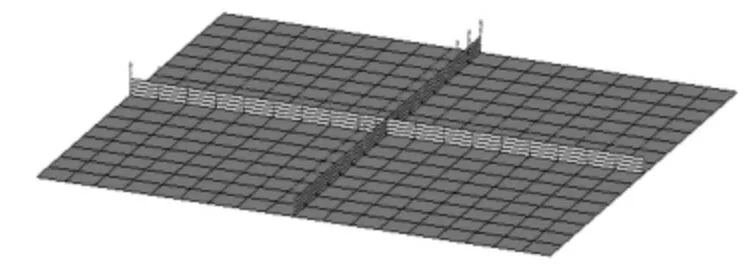
图5 形状变量2Fig.5 Shape design variable 2
在形状变量3 中,横向筋板为同一水平,纵向筋板中间位置高度最大并向四周逐渐线性减少(见图6)。
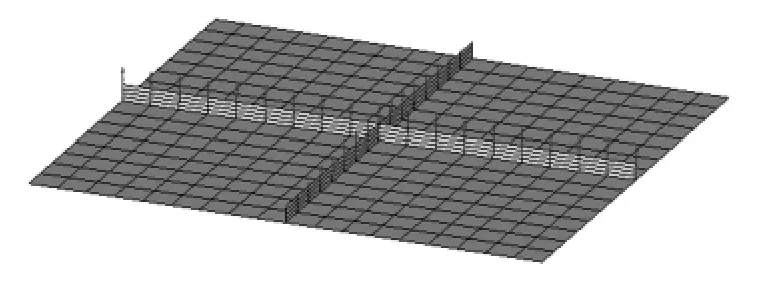
图6 形状变量3Fig.6 Shape design variable 3
在形状变量4 中,纵向筋板为同一水平,横向筋板中间位置高度最大并向四周逐渐线性减少(见图7)。
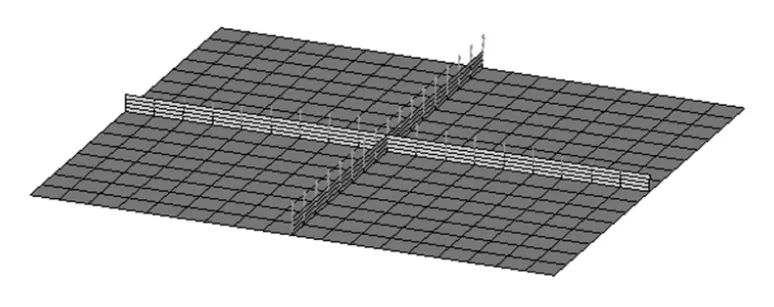
图7 形状变量4Fig.7 Shape design variable 4
建立4 个形状变量的目的是为了龙骨结构在优化过程中,能够尽可能地使全局优化算法考虑多种形状组合的可能性,使优化得出的结构具有较好的性能。
这些形状变量在优化过程中,将根据全局优化算法的响应进行作用,使龙骨结构有限元模型发生变化,并返回结构响应值。通过全局优化搜索,龙骨结构优化模型如图8 所示。
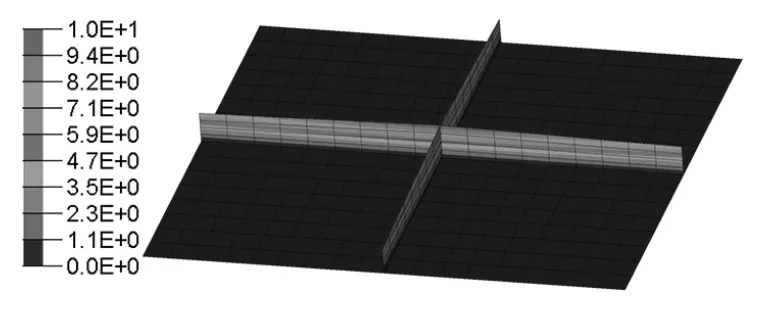
图8 全局优化结果Fig.8 Global optimization results
优化结果表明,在筋板交错的位置增加筋板高度能够有限提升龙骨结构整体刚度。其余位置可以采用较小的筋板高度。
4 结 语
1)为了提高船舶龙骨结构在受力过程中应力分布的均匀性和提高材料的利用率,本文采用Hypermesh 软件建立了龙骨结构有限元模型,并结合其MORPH 功能定义筋板形状变量,建立形状优化模型。
2)本文将全局优化算法与形状优化模型相结合,对船舶龙骨结构进行优化设计。结果表明,在筋板交错的位置增加筋板高度能够有限提升龙骨结构整体刚度。其余位置可以采用较小的筋板高度。
[1]姚谦峰,李挺,郭猛,等.密肋轻钢龙骨复合墙体的抗剪性能[J].天津大学学报,2011,44(7):587 -592.YAO Qian-feng,LI Ting,GUO Meng,et al. Shear bearing capacity on multi-ribbed composite wall with light-gauge steel[J].Journal of Tianjin University,2011,44(7):587 -592.
[2]左宏亮,武胜.腹板开孔标准轻钢龙骨力学性能比较研究[J].大连理工大学学报,2009,49(6):876 -883.ZUO Hong-liang,WU Sheng. Comparative research on mechanical behaviors of slotted standard steel studs in web plate[J].Journal of Dalian University of Technology,2009,49(6):876 -883.
[3]王昭俊,崔永旗,张素梅,等.腹板开孔轻钢龙骨复合墙体截面参数对传热的影响[J]. 哈尔滨工业大学学报,2006,38(10):1786 -1788,1792.WANG Zhao-jun,CUI Yong-qi,ZHANG Su-mei,et al.Study on heat transfer for sectional parameters of the slotted light steel - framed composite wall[J]. Journal of Harbin Institute of Technology,2006,38(10):1786 -1788,1792.
[4]耿瑞光,张洪田.基于多领域建模的气垫船推进轴系优化设计[J].舰船科学技术,2014,36(6):86 -91.GENG Rui-guang, ZHANG Hong-tian. Optimization research of hovercraft′s propulsion shafting based on multifield modeling[J]. Ship Science and Technology,2014,36(6):86 -91.
[5]陈龙,张金超,汪若尘,等.全簧载质量范围内超微型汽车悬架全局优化[J]. 江苏大学学报(自然科学版),2012,33(5):502 -507.CHEN Long,ZHANG Jin-chao,WANG Ruo-chen,et al.Global optimization of super mini vehicles suspension in full range of sprung mass[J].Journal of Jiangsu University(Natural Science Edition),2012,33(5):502 -507.
[6]朱经浩,何似菡.一类多项式全局优化的差分算法[J].同济大学学报(自然科学版),2014,42(5):804 -806,822.ZHU Jing-hao,HE Si-han. A difference algorithm to find global minimizers of a polynomial[J]. Journal of Tongji University (Natural Science),2014,42 (5):804 -806,822.
