面向大型船舶装备的系统可靠性预计方法研究

熊 尧，徐 巍，张文俊

(武汉第二船舶设计研究所，湖北 武汉430205)

0 引 言

系统可靠性预计是在装备研制阶段预先估计所设计系统在给定的工作条件下是否达到规定可靠性要求的一种方法，是寻找设计薄弱环节并作出更改设计的决策提供依据［1-2］。其基本原理是根据系统各部件的可靠性来推测系统的可靠性，是一种由下至上，贯穿于装备研制各阶段的综合过程［3-4］。

对于大型船舶装备而言，由于长期远离岸基，海洋环境多变，发生故障时无法得到岸上支援，严重故障发生后轻则丧失部分功能，重则艇毁人亡。因此，大型船舶系统相对飞机、电网、重型数控机床等大型设备而言，其固有可靠性要求更高。进而导致在该类装备的研制过程中，诸多重要设备均采用“热备份”(并联)、“冷备份” (旁联、表决结构)等设计措施以保障其固有可靠性水平，进而导致整个系统包含众多串、并、旁、表决结构，甚至是多种典型联接方式的混联结构，给系统的可靠性预计及评估等工作带来较大难度。

目前，常用的系统可靠性预计方法有数学模型法、应力分析法、专家评分法和数值仿真法［5-9］等，其中应力分析法适用于结构可靠性预计，修正系数法适用于组成零件为标准部件产品可靠性预计，专家评分法适用于部件故障率未知的可靠性预计，数学模型法适用于组成结构简单的系统可靠性预计。以上方法都有各自的局限性，对于船舶系统而言，由于系统任务可靠性模型非常复杂，系统各级产品寿命分布类型繁多，此时常用的可靠性预计方法难以满足整个系统可靠性预计的需要，如包含有串、并联的旁联系统可靠性框图，其任务可靠性数学解析公式将难以推导。数值仿真方法对复杂装备的系统可靠性预计问题具有极好的适应性，不但可以求解系统可靠性的点估计值，还可以得到统计值的分布函数，对深入了解系统可靠性有很大帮助，但该方法计算量较大、耗时较长，如果借助计算机的计算能力，则计算问题可有效解决。

本文提出一种基于蒙特卡罗(monte carlo)仿真的系统可靠性预计方法，该方法也称随机抽样方法，是以概率和数理统计为基础，以随机抽样法为手段，用概率随机生成模型及系统可靠性框图来近似计算系统可靠性预计值。本文先以简单系统为例，采用数学模型法和蒙特卡罗法分别计算系统可靠性，通过对比分析来验证基于蒙特卡罗仿真的系统可靠性预计法的正确性，进而以复杂系统为例来验证该方法适用范围的普适性。

1 基于蒙特卡罗法的系统可靠性仿真预计

蒙特卡罗法是以概率和统计理论为基础的一种计算方法，将所求问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解。蒙特卡罗方法又称统计模拟法或随机抽样技术。对于大型船舶系统而言，由于结构复杂、零部件繁多，将总体视为整体进行可靠性建模与仿真则难度极大，因此可将总体逐级划分，形成各级分系统，最后从底层分系统展开系统可靠性建模与仿真，进而向上集成最终实现总体可靠性建模与仿真。分层建模、仿真和集成过程如图1 所示。

图1 大型船舶系统的分级可靠性建模与仿真示意图Fig.1 Large ship system grading reliability modeling and simulating sketch map

在对总体开展分级可靠性建模、仿真与集成时，难点在于针对系统可靠性模型的仿真，本文采用蒙特卡罗方法对底层系统的可靠性仿真预计流程为:

1)依据各设备的可靠性指标(MTBF)及失效分布类型(指数分布、威布尔分布、正态分布)，采用随机抽样生成一个设备的正常工作时间(T)。

2)依据各设备的正常工作时间随机抽样值，结合表征设备故障关联关系的系统可靠性框图，推导系统的正常工作时间，得到一次仿真过程中系统工作时间的模拟值(T0)。

3)重复第1、2 步，直至仿真次数达到一定次数N(如1 000 次)。

4)依据各系统工作时间仿真数据的落点分布，经冒泡法进行大小排序后，通过区间统计方式得到系统的任务可靠性变化曲线。

算法流程图如图2 所示。

编制系统、总体工作时间的逻辑算法(如串联结构中，取工作时间最小值作为系统工作时间;在并联系统中，取工作时间最大值作为系统工作时间)，计算得到系统、总体的工作时间模拟值(T0)。

对于大型船舶装备中的电子、机械及机电类设备，其常见失效分布类型的随机抽样公式如下:

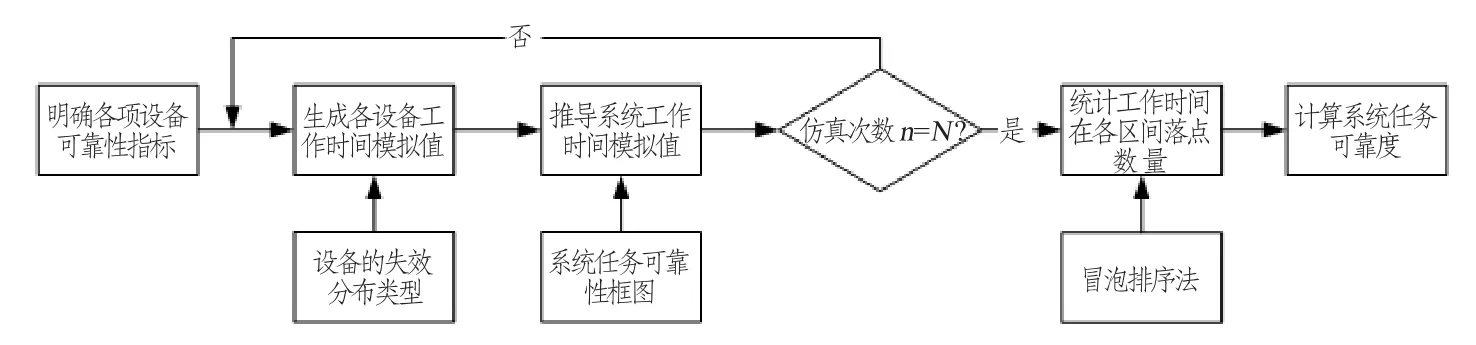
图2 基于蒙特卡罗仿真的系统可靠性预计方法流程图Fig.2 System reliability prediction method flow chart based on mento carlo simulation

1)二项分布

假设r 为(0，1)区间上均匀分布的随机变量，成败型设备的任务成功率为p，则某次任务成功与否的表征公式为:

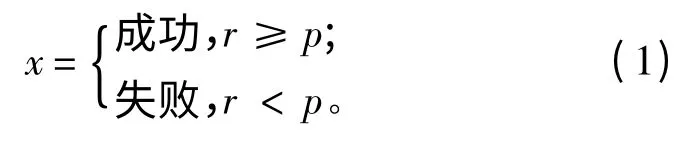
2)指数分布:

假设r 为(0，1)区间上均匀分布的随机变量，服从指数分布设备的故障率为λ，则工作时间t 的随机变量抽样公式为:

3)威布尔分布:

假设r 为(0，1)区间上均匀分布的随机变量，服从威布尔分布设备的参数为η、m，则工作时间t的随机变量抽样公式为:

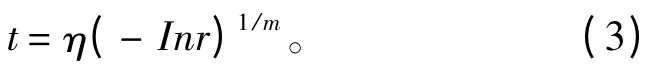
4)正态分布:

假设r 为(0，1)区间上均匀分布的随机变量，服从正态分布设备的参数为μ、δ，则工作时间t 的随机变量抽样公式为:

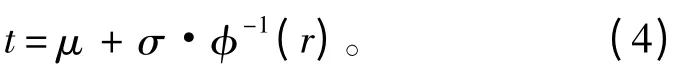
其中φ-1(r)表示标准正态分布的随机生成函数。

对于各类可靠性框图，系统工作时间的逻辑判断原则为:

1)串联系统

假设各设备的工作时间随机生成数为t1，t2，…，tn，则系统工作时间为:

2)并联系统

假设各设备的工作时间随机生成数为t1，t2，…，tn，则系统工作时间为:

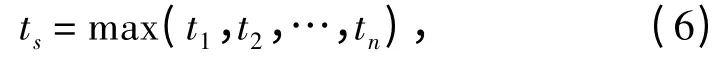
3)旁联系统

假设各设备的工作时间随机生成数为t1，t2，…，tn，则系统工作时间为:

4)m/n 表决系统

假设各设备的工作时间随机生成数为t1，t2，…，tn，则系统工作时间为:

其中，Tm指将t1，t2，…，tn从大到小排序后，排在第m 项的设备工作时间。

2 实例验证

2.1 系统可靠性仿真预计方法的精度验证

由于基于数学解析方法的可靠性预计方法应用广泛、认可度较高，因此其预计结果的准确度可作为其他预计方法的检验标准。本文以典型串、并、旁联混联系统为例(见图3)，验证基于蒙特卡罗仿真的可靠性预计方法的准确性。

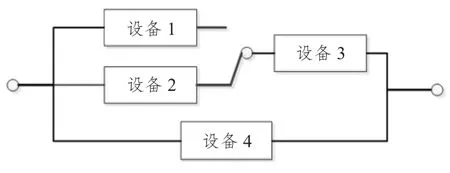
图3 典型简单旁、串、并混联系统可靠性框图Fig.3 Typical simple series ，parallel and bypass mix system reliability block diagram

框图中各设备均符合指数分布，各设备的可靠性指标为:

表1 各设备可靠性指数Tab.1 Reliability index of equipment

1)基于数学解析法的系统可靠性预计采用数学经验公式推导得到的系统可靠性预计公式为:

其中，旁联线路的可靠性计算公式为:

非旁联线路的设备可靠性计算公式为:

2)基于蒙特卡罗仿真的系统可靠性预计

采用蒙特卡罗随机抽样法，生成各设备的10 000次工作时间:

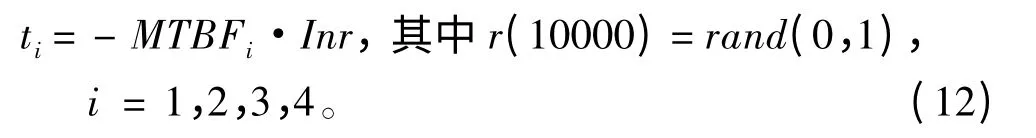
在一次仿真过程中，系统的工作时间为:

重复仿真10 000 次，得到系统工作时间集合:

对系统工作时间采用冒泡法排序，进而通过区间落点统计情况，得到系统在各个工作时间的可靠度R(t):

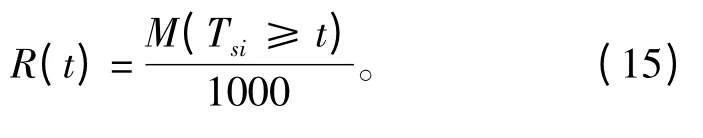
3)对比验证

以Matlab 为平台，编程实现基于数学解些公式和蒙特卡罗仿真分别预计得的系统在可靠度变迁曲线(0 ～1 000 h 内)，其中连续实线表示基于基于数学解析公式计算得到的系统可靠性预计值变化曲线，十字形间断曲线表示基于蒙特卡罗仿真方法计算的到的系统可靠性预计值变化曲线(见图4)。

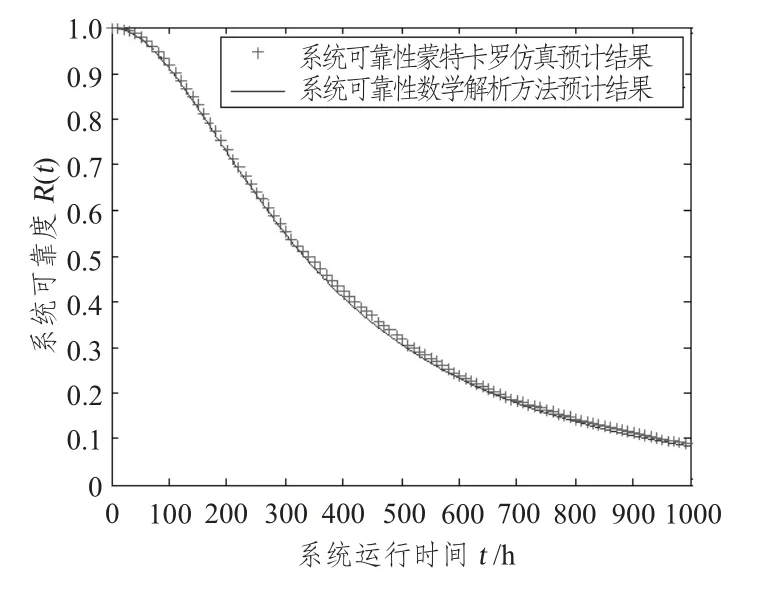
图4 数学解析法和蒙特卡罗仿真法的系统可靠性预计曲线对比图Fig.4 System reliability prediction curve comparison chart based on mathmetical formula and mento carlo simulation

从2 种方法分别计算得到的系统可靠性预计值变化曲线吻合程度来看，2 种预计方法的差值极小，因此在误差允许范围内，可以认为2 种方法的预计精度一样。

2.2 复杂系统可靠性预计适应性验证

对于某些设备为间断运行且串并联后再旁联的混联系统，数学解析方法难以推导出系统可靠度预计值的计算公式，针对这些复杂但常见的混联系统，蒙特卡罗仿真预计法能很好地进行可靠性仿真预计。以某船舶装备的操舵系统为例，验证基于蒙特卡罗仿真的可靠性预计方法相比数学解析法有更好的普适性。

依据操舵系统各设备的故障关联关系及功能备用关系，得到操舵系统的任务可靠性框图如图5 所示，可知该系统为泵控装置与集成模块串、并联后与伺服阀控旁联，最后与并联的舵角反馈机构和传动装置串联。

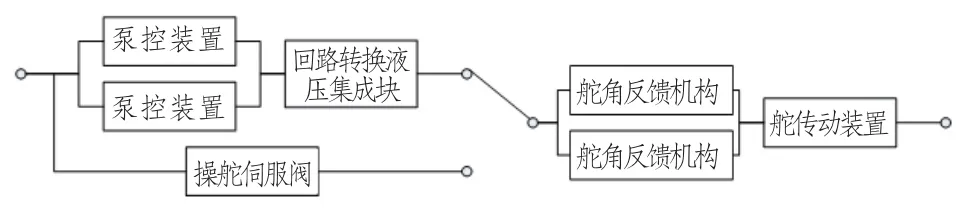
图5 某船舶装备的操舵系统可靠性框图Fig.5 Some ship equipment′s steering system reliability block diagram

系统中各设备的可靠性数据及失效分布类型如表所示。

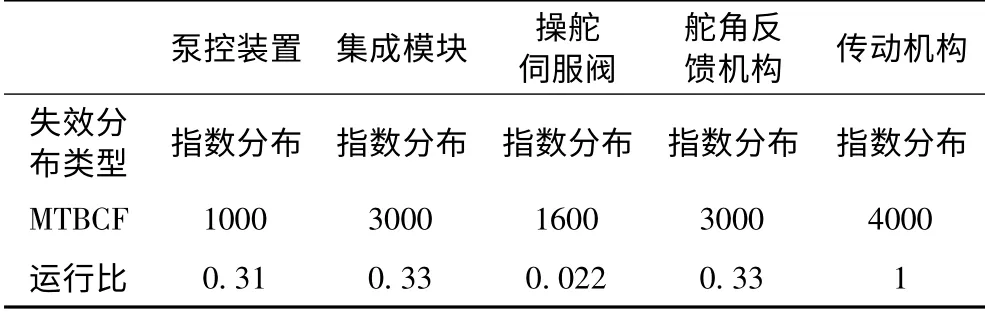
表2 可靠性数据及失效分布类型Tab.2 Reliability data and failure disribution type

假设泵控装置可靠度为R1(t1)，集成块为R2(t2)，伺服阀为R3(t3)，反馈机构为R4(t4)，传动装置为R5(t5)，首先需要先对方向舵和液压集成块的串并联结构进行公式推导，得到:

则旁联结构的任务可靠性数学公式为:

最后旁联结构和其他设备串并联后的系统任务可靠性计算公式为:

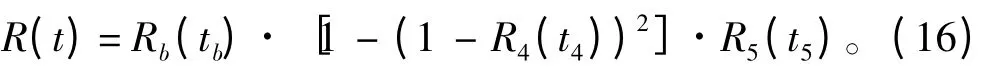
在旁联结构的任务可靠性Rb(t)的数学公式推导中，需要采用卷积公式对上下支路的可靠性公式进行双重积分，且开积分过程中各设备运行时间还各不相同。由此可见，对于此类较复杂的混联系统而言，其数值可靠性仿真模型的公式推导极其困难，甚至很可能无法推导出相应的解析公式。因此，数学解析方法对于此类的混联模型不具备工程应用价值。

依据2.1 节中蒙特卡罗仿真实施流程，在设备工作时间随机数抽样生成中加入运行比参数d，抽样公式如下:

系统在一次仿真过程中的工作时间逻辑解析公式为:

图6 为经10 000 次仿真后统计得到操舵系统的任务可靠性变化曲线。

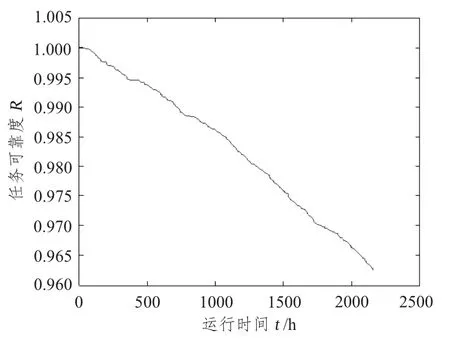
图6 某船舶装备的操舵系统可靠度预计值变化曲线Fig.6 Some ship equipment′s steering system reliability prediction value change curve

从仿真预计计算过程可以看出，对于包含间断运行设备和复杂旁联结构的系统而言，其实现难度与2.1 节中简单混联系统并无太大区别，再加上2 种方法的预计精度差别不大，因此可以综合认为基于蒙特卡罗仿真的系统可靠性预计方法的普适性更强。

3 结 语

在大型船舶装备的系统可靠性预计工作中，数学解析法虽然应用广泛、认可度高，但随着系统复杂程度提高，解析公式的推导难度逐渐增大甚至无法得到。基于蒙特卡罗仿真的系统可靠性预计方法则可以很好地解决复杂系统的公式推导问题，且经过预计结果对比分析发现，2 种方法的预计精度十分接近。因此，对于大型船舶装备的简单系统而言，公式推导简单、运算方便的数学解析方法更适合简单系统可靠性预计。对于复杂系统而言，普适性更强、原理更贴合实际的系统可靠性仿真预计方法将更加适用。此外，对于工作设备为可修状态的复杂系统时，蒙特卡罗仿真预计方法也同样适用，在后期研究过程中可进一步开展深入研究。

［1］王远达，宋笔锋. 系统可靠性预计方法综述［J］. 机设计，2008，28(1):37 -42.WANG Yuan-da，SONG Bi-feng. Overview of system reliability prediction method［J］. Aircraft Design，2008，28(1):37 -42.

［2］李瑞莹，康锐，党炜.机械产品可靠性预计方法的比较与选择［J］.工程机械，2009，40(5):53 -57.LI Rui-ying，KANG Rui，DANG Wei. Comparison and selection of prediction methods for mechanical products reliability［J］. Construction Machinery and Equipment，2009，40(5):53 -57.

［3］章国栋，陆延孝，屠庆慈，等.系统可靠性与维修性的分析与设计［M］.北京:北京航空航天大学出版社，1990:149 -168.

［4］陆廷孝，郑鹏洲.可靠性设计与分析［M］.北京:国防工业出版社，1997:78 -106.

［5］乔东，郑韵华，李建光.舰船可靠性设计计算及其应用研究［J］.舰船科学技术，1996，18(5):20 -29.QIAO Dong，ZHENG Yun-hua，LI Jian-guang. Ship reliability design calculation and application study［J］.Ship Science and Technology，1996，18(5):20 -29.

［6］安卫，吴晓平，陈国钧.基于神经网络的可靠性预计方法研究［J］.舰船科学技术，2002，24(S1):29 -31.An Wei，WU Xiao-ping，CHEN Guo-jun. Research of the method of reliability forecasting on neural networks［J］.Ship Science and Technology，2002，24(S1):29 -31.

［7］李四超，张代国，张强.机械结构可靠性计算方法［J］.舰船科学技术，2011，33(5):63 -65.LI Si-chao，ZHANG Dai-guo，ZHANG Qiang. Research on the improved calculation method for mechanical structural reliability［J］.Ship Science and Technology，2011，33(5):63 -65.

［8］吴晓平，汪玉，庞之洋. 基于模糊分析的× × 型电子调速器的可靠性预计与评价［J］.舰船科学技术，2006，22(6):31 -33.WU Xiao-ping，WANG Yu，PANG Zhi-yang.The reliability estimating and evaluating for × × electricre gulator because of the fuzzy analysis［J］. Ship Science and Technology，2006，22(6):30 -32.

［9］袁立峰，王浚.可靠性数字仿真方法及其应用［J］，电子产品可靠性与环境试验，2005(2):17 -20.YUAN Li-feng，WANG Jun. The method of reliability numerical simulation and its application［J］. Electronic Product Reliability and Environmental Testing，2005(2):17 -20.