自适应粒子群优化的船舶动力定位云模型控制器设计
2015-12-19郭丹丹
李 众,郭丹丹
(1. 江苏科技大学 电子信息学院,江苏 镇江212003;2.常州信息职业技术学院 电子与电气工程系,江苏 常州213164)
0 引 言
船舶动力定位系统是指利用自身推力系统产生反力和反力矩以抵抗风、浪和流作用于船上的环境外力和力矩,使船舶保持一定的位置和角度或按照预定轨迹运动[1]。与传统锚泊系统相比,其具有不受水深影响、机动性强、操作方便、定位精度高等优点。
随着控制理论和技术的发展,近年来一些智能化的控制方法开始应用到动力定位控制方面,比如模糊控制、鲁棒控制、神经网络控制等。云模型是一种新兴的智能控制算法,其基本思想是利用计算机来实现人的控制经验,所采用的云模型定性推理方法不要求给出被控对象的精确数学模型,同时可以保留被控对象及其环境中各种未知的不确定性因素。鉴于此,本文基于一维多规则推理映射算法设计了船舶动力定位云模型控制器。针对云模型控制器需要整定的参数较多,依赖于人工经验的整定难以达到理想效果,引入自适应粒子群优化算法对控制器参数进行优化整定,仿真结果表明改进的云模型控制器具有良好的控制性能。
1 船舶运动数学模型
对于动力定位船舶来说,通常情况下只需考虑六自由度运动中的纵荡、横荡和首摇[2]。为描述船舶的水平运动,建立如图1 所示的船舶运动参考坐标系,OEXEYE为大地坐标系,OXY 为随船坐标系,随船坐标系的原点在船舶重心处。定义大地坐标系下的船舶位置和首摇角η=(x,y,ψ),随船坐标系下的速度向量ν=(u,v,r)。
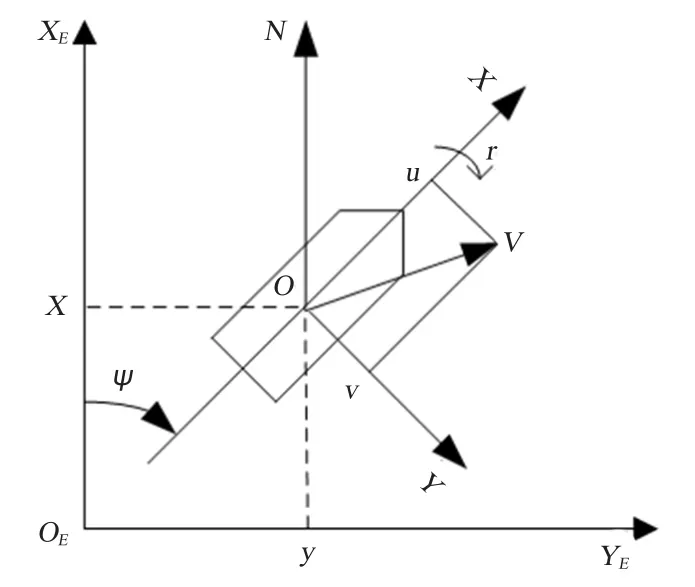
图1 船舶水面运动坐标系Fig.1 The coordinate system of ship surface movement
1.1 船舶运动低频数学模型
动力定位水面船舶的非线性低频运动为:
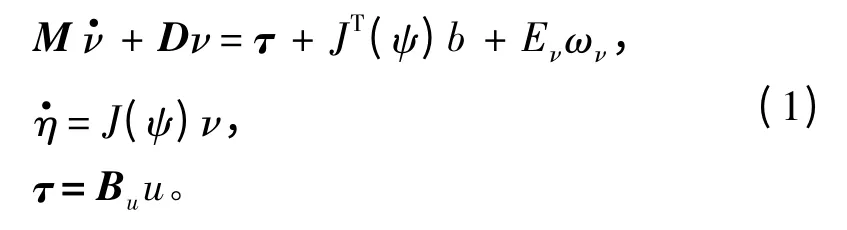
式中:M 为惯量矩阵;D 为由波浪漂移阻尼和层流表面摩擦产生引起的阻尼矩阵;τ 为由推力系统提供的力和力矩的控制向量;b 为由风、浪及流引起的未建模外力和力矩;Eν为系统噪声的幅值;Bu为描述执行机构的常数矩阵;u 为控制输入。
1.2 船舶运动高频数学模型
船舶的高频运动实际上是对一阶波浪的响应,在位置和角度上可以看作是附加了阻尼项的二阶谐波振荡器
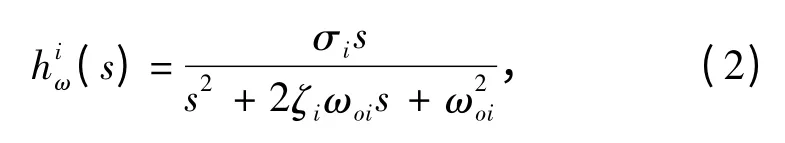
式中:ωoi(i=1 ~3)为波浪主导频率;ζi(i=1 ~3)为相对阻尼系数;σi(i=1 ~3)与波浪强度有关。
1.3 环境力模型
1.3.1 低频风模型
一般采用前馈控制方式来抵消风作用力的影响,风对船舶纵荡、横荡和首揺3 个自由度方向上的平均作用力和力矩可用下式计算:
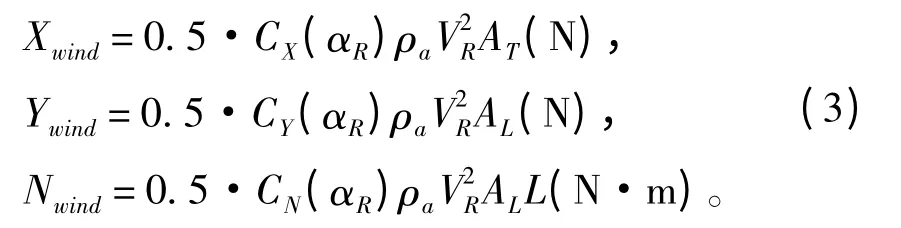
式中:CX和CY为风力系数;CN为风力矩系数,可由Isherwood 经验公式求得;ρa为空气密度,kg/m3;AT和AL为正投影面积和侧投影面积,m2;L 为船舶总长,m;VR为相对风速,kn。
1.3.2 偏差模型
由风、二阶波浪漂移力、海流、推力器损失及其他未建模动态引起的慢变环境扰动力和力矩,可用如下一阶高斯-马尔可夫过程估计:
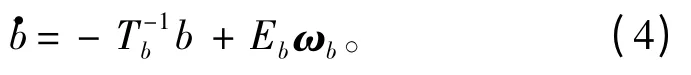
式中:Tb为关于位置和首向正定偏差的时间常量对角阵;Eb为环境扰动力幅值的三维对角阵;ωb为零均值高斯白噪声向量。
1.4 测量模型
船舶实际运动是高频往复运动ηω与船舶低频运动η 的叠加,且船舶测量系统提供的是带有测量噪声的船舶位置和首揺角度值,因此系统的测量模型为
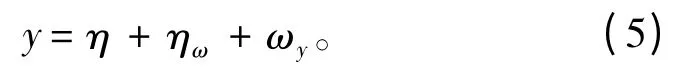
式中ωy为零均值高斯白噪声。
2 云模型控制器(CMC)
2.1 云模型控制原理
云模型是一种实现定性概念与定量数据相互转换的不确定性转换模型,它用3 个数字特征:均值(Ex)、熵(En)和超熵(He),将概念的随机性与模糊性融为一体[3]。设U 是一个用精确数值表示的定量论域,C 为U 上的定性概念,若定量值x ∈U,且x 是定性概念C 的一次随机实现,x 对C 的确定度μ(x)∈[0,1]是有稳定倾向的随机数,则x 在U 上的分布称为云模型[4]。

CMC 实现的输入输出控制本质上是一种映射关系,即偏差输入到控制量输出的映射。这个映射由1 组云模型IF X,THEN Y 规则来完成,其中X 是规则前件,表示为(Ex,Enx,Hex);Y 是规则后件,表示为(Ey,Eny,Hey)[5]。如果已知云模型(Ex,Enx,Hex),并有特定输入x= x0,则称为X 条件云模型,记为CGX;如果已知云模型(Ey,Eny,Hey),并有特定输入μ(x)= μ(x0),则称为Y 条件云模型,记为CGY。
X 条件云模型:
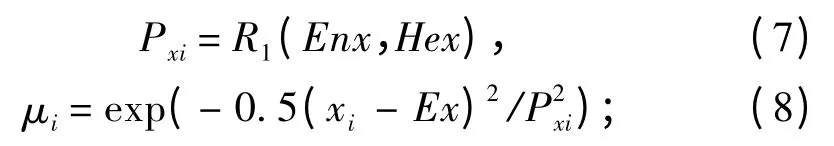
Y 条件云模型:
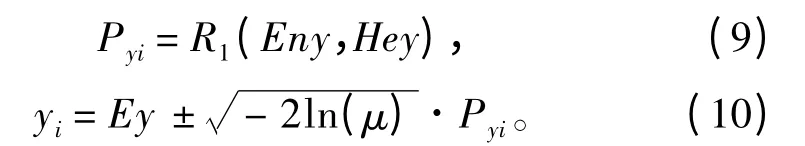
式中:R1(A,B)为服从正态分布的随机数;A 为期望值;B 为标准差。
考虑图2 所示的具有N 条定性规则的一维云模型映射器,其形式化描述为:IF X=Xi,THEN Y=Yi,i=1,2,…,N。偏差输入e 刺激不同规则的前件部分CGX1~CGXN,产生不同的μNj值,再经规则后件云发生器CGY1~CGYN处理,产生大量的云滴drop(yNjk,μNj),这些云滴经过加权平均处理后,最终得到与输入e 相对应的定量输出值u,即e 到u 的映射。
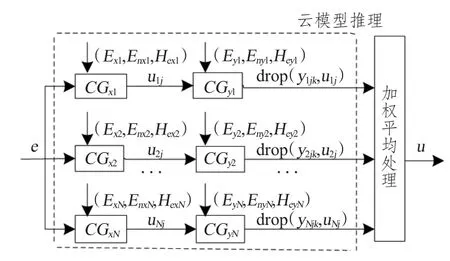
图2 一维云模型映射器Fig.2 The mapping processor of 1 -D cloud model
2.2 云模型控制器设计
基于上述设计的一维云模型映射器,构造如3所示的船舶动力定位云模型控制系统。为简单起见,记纵荡偏差eX到纵向控制输出uX的映射为一维云模型控制器C1;横荡偏差eY到横向控制输出uY的映射为一维云模型控制器C2;首揺偏差eψ到首向控制输出uψ的映射为一维云模型控制器C3。Kq(q=1 ~3)为驱动因子,Ci(i=1 ~3)均采用七规则推理,根据调试经验规则前件和规则后件云模型的特征参数设置如表1 所示。
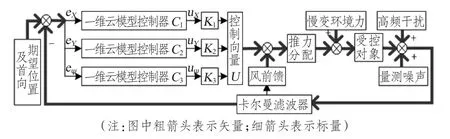
图3 船舶动力定位云模型控制系统框图Fig.3 Dynamic ship positioning cloud model control system
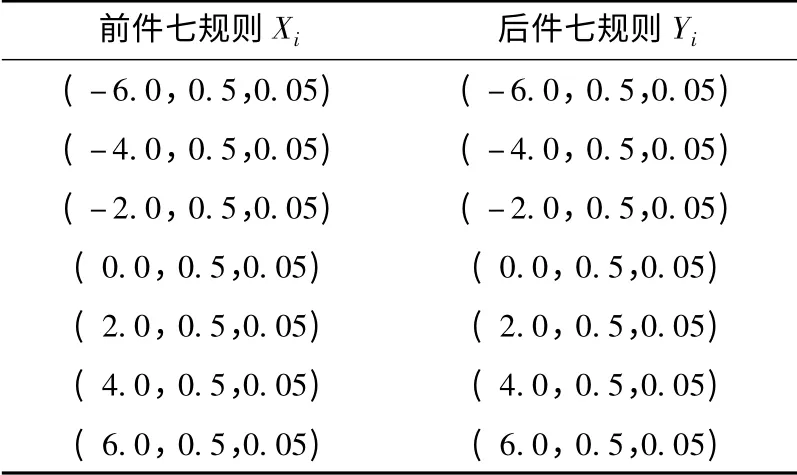
表1 控制器的云参数Tab.1 Cloud model parameters of CMC
上述设计中驱动因子、云模型3 个数字特征值的选取,规则库的建立全赖人为设定和不断试验,需要整定的参数众多。此外横荡和首揺方向的运动还存在耦合,完全依靠经验调试耗时繁琐且难以达到最优控制效果。为此,本文引入自适应粒子群优化理论对CMC 的控制参数进行优化整定。
3 自适应粒子群优化算法
3.1 标准粒子群优化算法
粒子群优化算法(PSO)是Kennedy 和Eberhart受鸟群觅食行为启发于1995 年提出的一种全局优化算法,通过种群中粒子间的合作与竞争产生的群体智能指导优化搜索[6]。粒子群优化算法应用于云模型控制器的参数寻优,其突出优点是不追究控制器推理规则和控制对象的模型结构,只针对参数本身进行全局搜索以达到优化的目的。
PSO 的数学描述如下:假设群体中N 个粒子在D 维搜索空间中以一定的速度飞行,粒子i 的当前位置为xi= (xi1,xi2,…,xiD),当前飞行速度为vi=(vi1,vi2,…,viD),个体最优位置为pbesti= (pbesti1,pbesti2,…,pbestiD)。设f(x)为最小化的目标函数,则粒子i 的当前最优位置由下式确定:

全局最优位置gbest(t)为
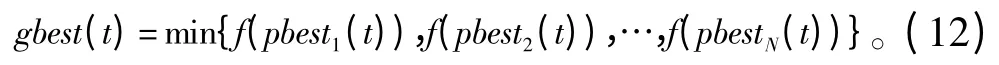
粒子的速度与位置更新方程为:
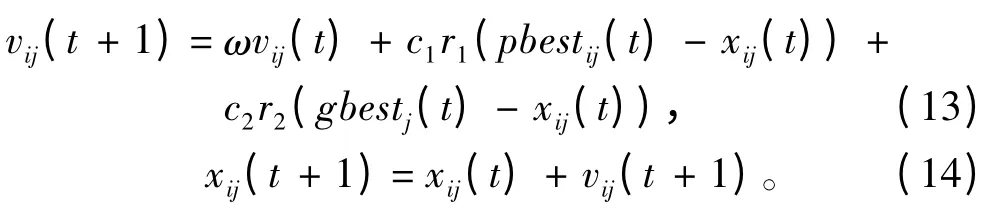
式中:ω 为惯性权重;t 为当前迭代次数;c1和c2为学习因子;r1和r2为[0,1]内随机数。
3.2 自适应粒子群优化算法(APSO)
PSO 算法存在早熟和局部收敛的问题,而出现早熟的关键是快速收敛时种群多样性的丧失。在自适应粒子群算法中,为了保证种群的多样性,第一引入自适应权值ω;第二对超出边界的粒子进行变异操作;第三通过对速度的动态限幅实现步幅调节。
惯性权重ω 对种群的局部搜索能力、全局搜索能力及收敛速度有着直接影响,研究发现较大的ω值有利于跳出局部最优,进行全局搜索;较小的ω值有利于局部寻优,加速算法收敛。根据粒子适应值的大小,本文将种群分为3 个适应值等级不同的种群,对不同种群的粒子采取不同的惯性权重调整策略,具体方法如下:
假设fi为粒子i 的适应值,favg为当前粒子平均适应值,fgood为适应值优于favg的粒子的平均适应值,fbest为当前全局最优适应值,ωmin和ωmax分别为最小、最大权值。
1)优秀种群:fi≤fgood,该部分粒子己比较接近局部最优点,所以应赋予较小的惯性权重以避免其跳过局部最优点。

2)一般种群:fgood<fi≤favg,该部分粒子彼此之间适应值相差较大,为更好地利用其全局寻优能力和局部寻优能力,利用X 条件云发生器非线性动态调整粒子i 的惯性权重。
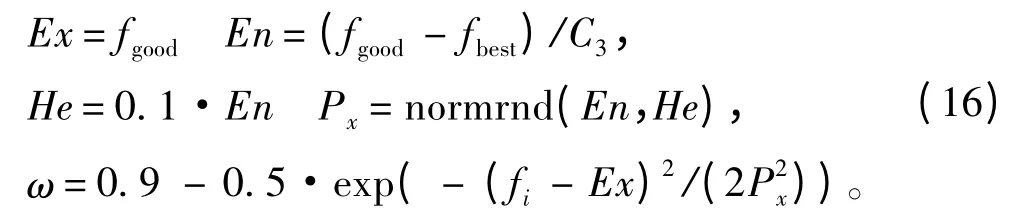
式中:C3为控制参数,本文取3。ω 随着粒子适应值的减小而减小从而实现了较优粒子获得较小ω。
3)劣种群:fi>favg,这些粒子为群体中较差的粒子,与全局最优点尚有一段距离,因此应赋予较大的惯性权重使粒子群有更大机会跳出局部极值,增强粒子的全局寻优能力。

PSO 算法中当某个粒子在搜索过程中飞出可行域时,通常的处理方法是使该粒子的位置处于边界上。其缺点是如果边界附近存在着局部最优则易使粒子陷入该局部最优点而产生停滞;另外还会使多个粒子在多个维度上都向边界聚集,若干次迭代后这些向边界聚集的粒子的行为将不可避免地趋于相同,从而降低了整个粒子群的多样性。在本算法中,对超出边界的粒子采取如下方式进行变异:
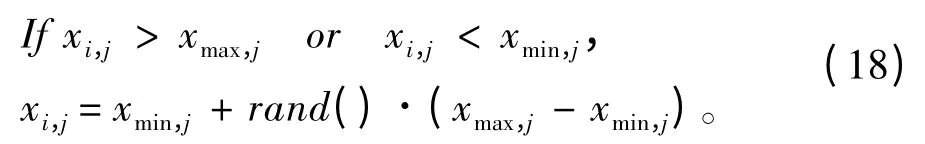
式中:xmax,j和xmin,j分别为粒子第j 维的上下界。这样的变异操作既确保了粒子在可行域内搜索,又克服了标准PSO 算法边界策略会导致粒子陷入边界局部最小的缺点,同时增加了变异性使得不同粒子的轨迹和行为不同。
4 基于APSO 算法的CMC 优化设计
4.1 适应度函数的选择
ITAE 指标是综合考虑稳态误差和调节时间的性能指标,以其较好的实用性和选择性得到了广泛的应用,故本文选用ITAE 指标来评价系统的动态性能。
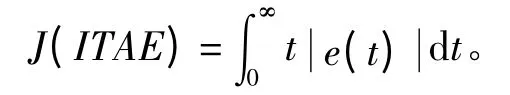
动力定位控制系统同时采用3 个云模型控制器,所以目标函数选择为:
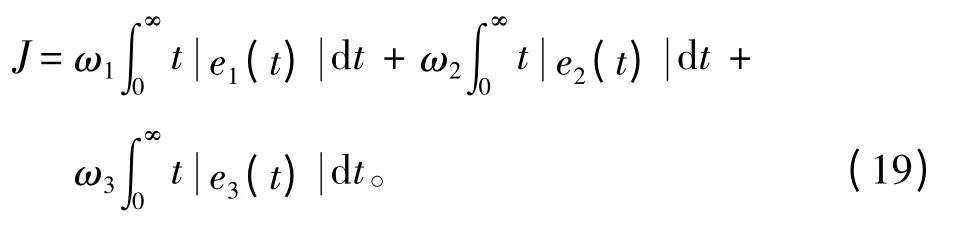
其中ω1,ω2和ω3为加权系数。
4.2 APSO-CMC 算法流程
适应度函数确定后便可以对如图3 所示CMC 的81 个参数进行寻优,分别是Kq(q=1 ~3);规则前件云参数(Exij,Enxij,Hexij)(i = 1 ~3,j = 1 ~7),其中Exi1= -6,Exi7= 6,Hexij= 0.1Enxij;i 为云模型控制器i,j 为第j 条推理规则。规则后件云参数(Eyij,Enyij,Heyij)(i,j 含义同上),其中Heyij=0.1 Enyij。在满足约束条件下,目标函数值最小时所对应的参数即为最优控制器参数。算法具体步骤为:
步骤1 随机初始化N 个粒子的速度和位置,pbesti为粒子当前位置,gbest 为当前全局最优位置。
步骤2 根据式(15 -17)计算ω,按式(13)更新当前粒子速度,再按式(20)对速度进行动态限幅。
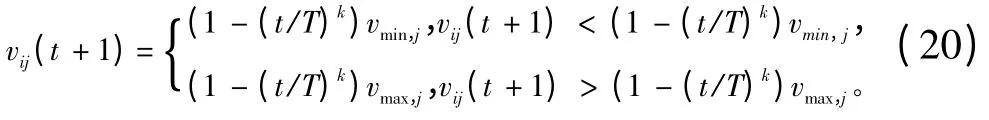
步骤3 按式(14)更新当前粒子的位置,再执行式(18)进行变异操作。
步骤4 将每个粒子的位置向量依次作为CMC参数代入图3 所示系统进行仿真,按式(19)计算J,再按式(11)更新pbesti。
步骤5 根据式(12)更新gbest。
步骤6 检查终止条件,若t 小于最大迭代次数T,则返回步骤2;否则终止迭代,并输出gbest。
5 仿真研究
在Matlab7.0 环境下,以一艘供给船为受控对象[7]进行仿真研究。该供给船的质量m = 4.591 ×106kg,船长L = 76.2 m,船宽B = 18.8 m,无量纲惯性矩阵和阻尼矩阵分别为:

假设船舶的初始位置为(0 m,0 m,0°),定位点为(50 m,50 m,10°)。
针对上述对象,利用APSO -CMC 设计方法对云模型控制器的参数进行优化。取粒子数N = 40,最大迭代次数T = 50,ωmax= 0.9,ωmin= 0.4,寻优过程曲线如图4。寻优结果为:K1= 0.006 8,K2=0.052 2,K3= 0.001 8,控制器Ci(i = 1 ~3)的控制规则云模型特征参数如表2 ~表4 所示。
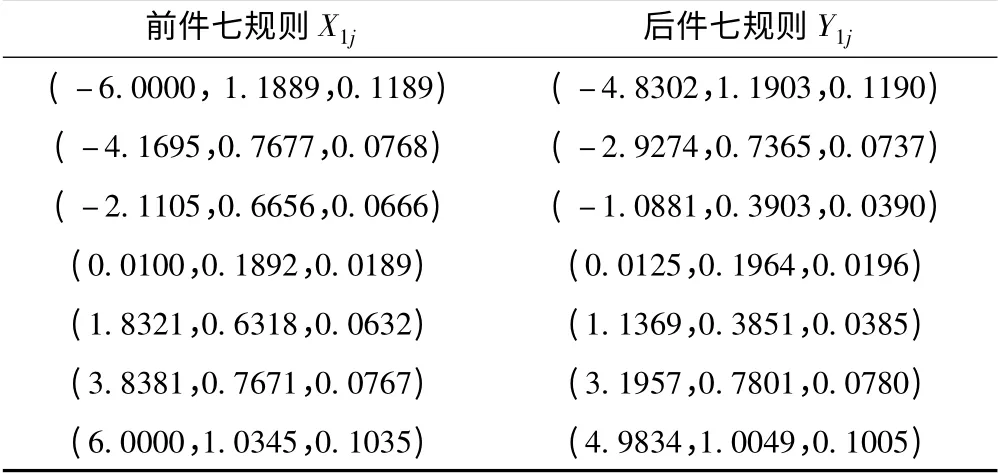
表2 控制器C1 云参数Tab.2 Cloud model parameters of controller C1
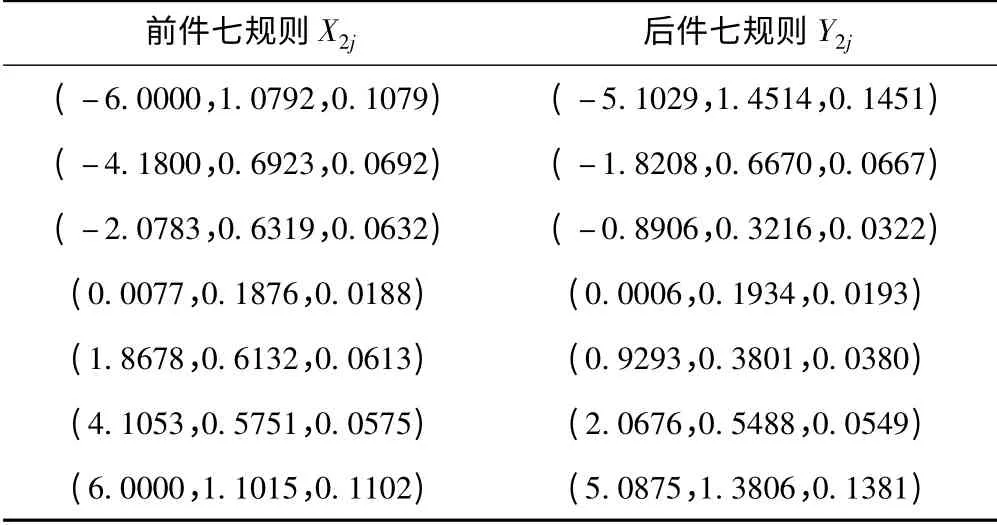
表3 控制器C2 云参数Tab.3 Cloud model parameters of controller C2
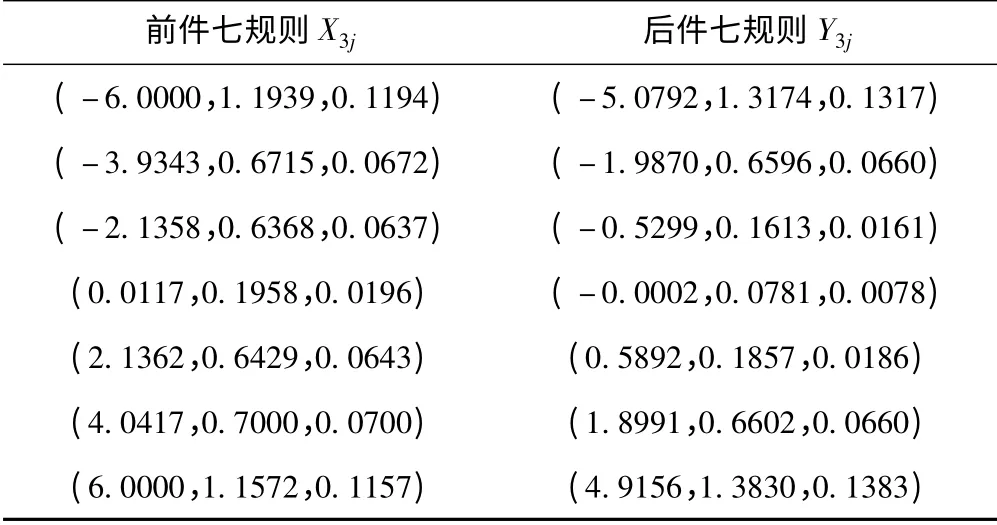
表4 控制器C3 云参数Tab.4 Cloud model parameters of controller C3
为验证所设计的船舶动力定位CMC 和APSO -CMC 的控制性能,在理想海况条件下,将CMC、APSO-CMC 控制的船舶3 个自由度运动效果与目前动力定位系统应用非常广泛的LQG 控制[8]的控制效果进行对比。取仿真时间为500 s,仿真结果如图5所示。
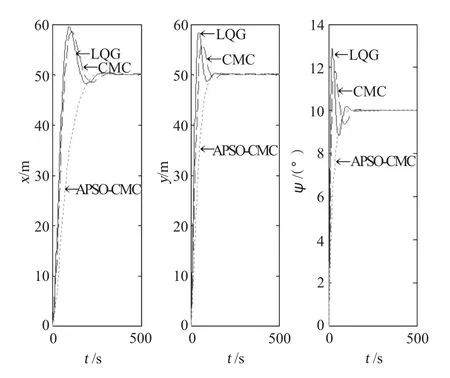
图5 理想海况下的动力定位响应曲线Fig.5 Response of designed controllers in ideal sea conditions
3 种控制器能够满足控制要求,但LQG、CMC纵荡、横荡和首揺响应的调节时间分别为257 s,128 s,140 s 和281 s,162 s,135 s,超调量分别为18.9%, 16.8%, 28.8% 和 17.2%, 12.1%,18.2%;APSO-CMC 在3 个方向上响应的调节时间则为238 s,119 s,100 s,响应曲线平滑无超调。可见与LQG 相比,CMC 虽调节时间略长,却使超调量大幅降低。APSO-CMC 利用APSO 算法的自寻优特点找到了合适的CMC 特征参数,不仅大大缩短了设计周期,而且在调节时间、超调量、稳态精度上均有显著提高;其控制效果明显优于LQG和CMC。
6 结 语
动力定位一直以来是控制学领域研究的重点内容,它关系到船舶和海洋平台作业的安全性和可靠性。本文在对粒子群优化算法和云模型控制理论深入研究的基础上,提出了基于APSO 算法的动力定位CMC 优化设计方法。所采用的云模型控制无需冗繁的推理计算,能够直接实现定量输入、并行定性推理、定量输出的控制过程,实时性强。同时APSO 通过引入自适应权值、变异操作和动态限速能很好避免早熟收敛,提高粒子全局搜索能力。APSO - CMC 较大程度地提高了系统的控制性能,具有一定的实用价值。
[1]周利,王磊,陈恒. 动力定位控制系统研究[J]. 船海工程,2008,37(2):86 -90.ZHOU Li,WANG Lei,CHEN Heng.Review on the study of dynamic positioning control system for vessels [J].Ship&Ocean Enginering,2008,37(2):86 -90.
[2]WANG Li-yun,XIAO Jian-mei,WANG Xi-huai.Ship dynamic positioning systems based on fuzzy predictive control[J]. Telkomnika-Indonesian Journal of Electrical Engineering,2013,11(11):6769 -6779.
[3]高键,李众.一维云模型映射器设计及其应用研究[J].系统仿真学报,2006,18(17):1861 -1865.GAO Jian,LI Zhong. Study on design and application of one-dimension cloud model mapping processor[J]. Journal of System Simulation,2006,18(17):1861 -1865.
[4]李德毅.三级倒立摆的云控制方法及动平衡模式[J].中国工程科学,1999,1(2):41 -45.LI De-yi.The cloud control method and balancing patterns of triple link inverted pendulum systems[J]. Engineering Science,1999,1(2):41 -45.
[5]李众,刘艳.一维正态云模型单规则推理映射研究[J].系统仿真学报,2008,20(3):702 -705.LI Zhong,LIU Yan. Research on one - dimension normal cloud model single rule reasoning[J]. Journal of System Simulation,2008,20(3):702 -705.
[6]刘峰,韩艳丽,王铎.自适应权重粒子群优化的粒子滤波算法[J].计算机仿真,2013,30(11):330 -333.LIU Feng,HAN Yan-li,WANG Duo. Particle swarm optimization particle filtering algorithm based on adaptive weight[J].Computer Simulation,2013,30(11):330-333.
[7]王丽娜.船舶动力定位系统控制器的设计与仿真[D].大连:大连海事大学,2012.WANG Li-na.Controller design and simulation of dynamic positioning system [D]. Dalian: Dalian Maritime University,2012.
[8]边信黔,付明玉,王元慧.船舶动力定位[M].北京:科学出版社,2011:164 -173.BIAN Xin-qian,FU Ming-yu,WANG Yuan-hui.Ship dynamic positioning[M].Beijing:Science Press,2011:164-173.
