基于高精度近似模型的舰船线型优化
2015-12-19付雪峰
刘 鹏,付雪峰
(中国船级社舟山办事处,浙江 舟山316000)
0 引 言
船舶线型优化关系着性能,是船舶总体设计的重要方面。其设计的原则在于满足总布置要求的前提下,确保外形光顺,从而保证船舶水动力性能。因此舰船的线型优化一直是型线设计的主要工作内容。随着CFD 技术的发展,数值模拟在性能预报中扮演了越来越重要的角色,不仅提高了时效性,也提高了性能预测的精度。
将CFD 计算与优化计算相结合最大的难题在于解决计算的时效性。通常采用2 种方式[1]:一种是直接将CFD 计算与优化计算集成,通过提高计算机计算能力,来缩短计算时间,该方法对于大尺度模型效果有限,同时数据计算、分析工作量大,时效性差,难以适应设计需要;另一种是通过大量的仿真计算寻求线型参数变化对子学科的影响规律,得出规律后寻求相对优化结果,该方法可得出线型参数影响规律,但容易求得局部最优的结果,优化结果精度不高。目前,舰船线型优化多是采用第2 种方法。
近年来,通过构建代理机制减少高精度仿真计算次数成为多学科优化领域研究的热点。本文拟构建一种优化模式,将CFD 计算软件与优化计算软件集成,通过合理交叉应用,实现对舰船线型快速多学科优化。
1 基本原理
现代舰船总体设计对线型提出了更高要求,线型设计不仅要实现快速性最优,对水动力噪声、操纵性等都提出了优化要求。因此有必要对线型开展多学科优化设计。
基于高精度近似模型的线型优化方法包含以下几个基本阶段[2-3]:
1)方案筛选。主要有试验设计法和计算机试验设计/分析法等。其目的在于通过对设计变量组合方案的选择,将能够涵盖整个函数特性的设计变量组合拣出,生成样本点方案,从而减少后期CFD 计算的次数。
2)高精度模拟数据库构建。对样本点方案逐个进行高精度CFD 计算分析,获得输入和输出数据。其目的在于对每个样本点进行流场模拟计算,并分析样本点特性,生成子学科预报数据库。
3)子学科预报模型构建。用拟合的方法拟合生成子学科样本数据,构造出近似模型,并对该近似模型的可信度进行评估,构造近似模型的主要方法有响应面法、人工神经网络法、Kriging 模型等。通过构造近似模型,可以避免对后期生成的临时样本进行CFD 计算,仅需要通过拟合方法,对临时样本进行预报,这样就使得优化计算的工作量大大前移。如果前期的样本点数据库建立的足够完善,后期的优化就无需大量采用高精密分析模型。
海洋上有好几只无形的“手”能随时拨弄海面上孤零零的冰山——海风、洋流能直接推动冰山转向;日晒和气温升高能让冰山融化,改变冰山的形状。
4)多学科优化框架构建。由于子学科间存在耦合关系,通过样本参数的组合,避免对子学科之间信息交互的求解;通过对权系数的调整,结合不同的多学科优化算法,可求得不同优化目标下系统级最优方案参数组合及相应的各学科预报结果。
2 典型算例
在本算例中,对水下回转体基本线型进行优化,变量间外形函数关系[4-6]如下:
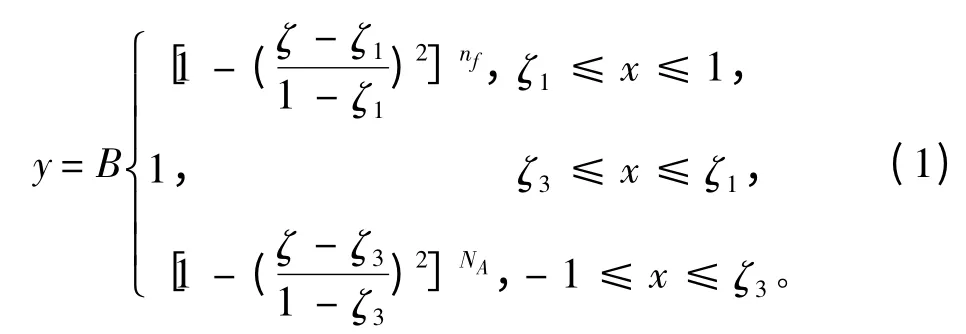
式中:x 和y 的意义见图1;ζ=2x/L 为x 的无量纲坐标值;na和nf为回转体后体及前体的丰满度系数。

图1 艇体外形示意图Fig.1 The revolution submarine with parallel
将快速性与水动力噪声作为优化的2 个子学科,对回转体的线型进行综合优化,构建如下优化模型:
优化目标:min F=ω1× A + (1 - ω1)× R,
约束条件:V=C1。
设计变量:宽度B,m;总长L,m;进流段长度Lf,m;去流段长度La,m;浮心纵坐标Xc,m;回转体排水体积V,m3。
各系数及设计变量的值域变化范围如表1 所示。
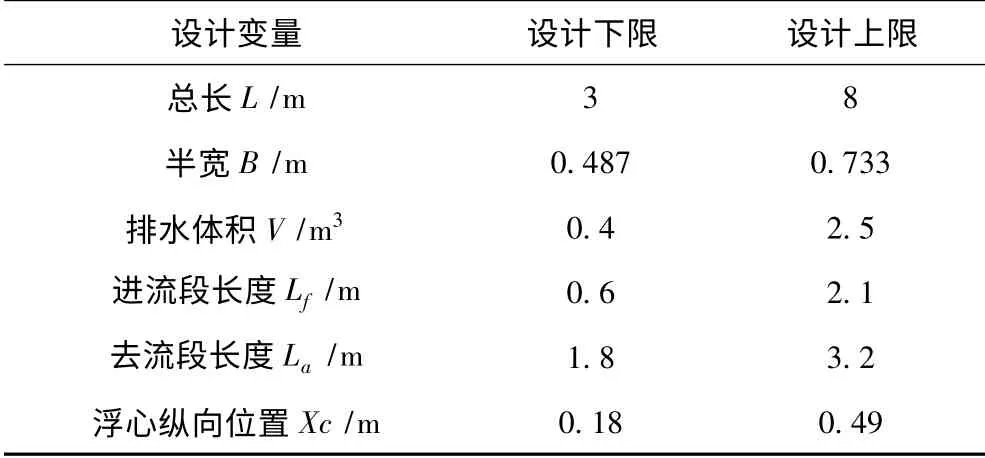
表1 主要参数及值域表Tab.1 The main parameter range
为体现各子学科在多学科问题中的权重关系,给定阻力R 和水动力噪声A 在目标函数中的权重ω1和(1 -ω1),由此进行优化得到唯一最优解及该最优解条件下回转体的形状控制参数。线型优化设计主要建模步骤如下:
1)回转体线型方案筛选
为了减少多参数连续设计变量的计算代价,需要对样本点进行筛选。从而获得能够涵盖全值域的设计样本。以正交试验法得到的系列设计变量为输入,快速构建回转体线型方案的三维模型,作为下一个模块——CFD 计算模块的输入。根据表1,在设计变量值域范围内,设立10 个水平,通过正交试验法进行回转体线型的组合,得到了90 个线型组合方案。并据此建立三维模型。
2)子学科数据库构建——基于CFD 方法的回转体快速性和水动力噪声计算
采用Fluent 计算软件,对建立的方案分别进行流场和水动力噪声场的数值模拟,计算结果如图2所示。
根据计算结果,建立潜艇的阻力、水动力噪声数据库,该数据库为近似模型建立的基础。该项工作量大、耗时长。但该数据库的建立对于子学科的快速预报意义重大,对预报精度有着重要影响。
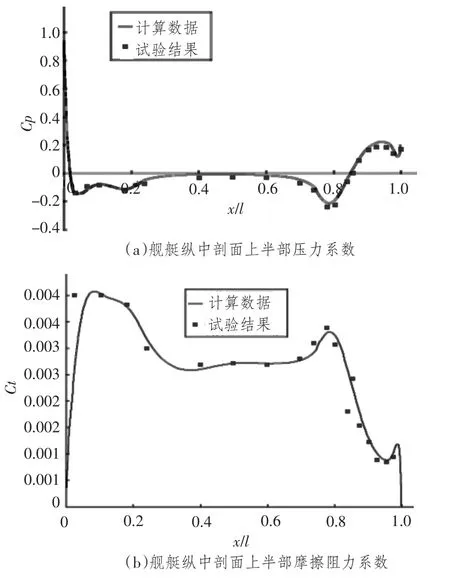
图2 艇体纵中剖面上半部压力系数Fig.2 The pressure coefficient on upper longitudinal
3)近似模型构建——基于神经网络的响应面的建立以及快速预报的实现
通过样本点的生成,大大减少CFD 数值计算的次数。而要将多学科化框架应用于实际的设计中,这种计算速度还是不够的,需建立近似模型,实现快速预报。通过对样本点三维模型的CFD 计算,构建起阻力和水动力噪声数据库。针对数据库,建立响应面模型,并实现快速性和水动力噪声的快速预报及优化。这样就将大量的数值计算工作转移至前期的技术储备中,在实际优化设计中,通过响应面模型,短时间内即可实现潜艇线型的快速性和水动力噪声的预报及综合优化。因此,前期的数值计算、分析工作越完善,数据库中储存的模型种类越多,可形成数值水池,整个代理模型的应用范围才会广泛。
4)线型的综合寻优
对低阻低噪线型综合优化,当给定权重ω1= 0,则为单目标优化,优化目的为快速性最优,相应的设计变量即为快速性最好的线型的参数。对于此时的优化模型,可采用序列二次规划法(NLPQL)进行优化。
当给定权重ω1= 0.5,优化目标为快速性和水动力噪声同等重要的情况下,寻求线型最优的艇型参数方案,在isight 平台下,优化框架如图3 所示。此时,对每个学科采用的优化方法为序列二次规划法(NLPQL),系统级为协同优化。优化结果见图4、表2 和表3。
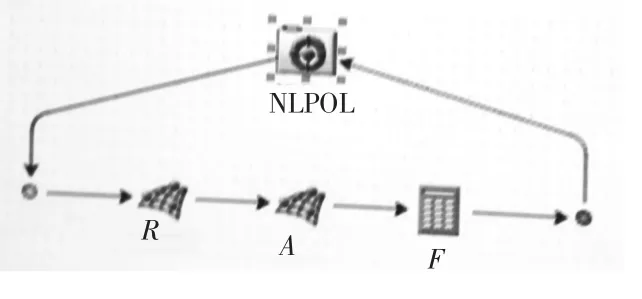
图3 集成优化框架Fig.3 The optimization model
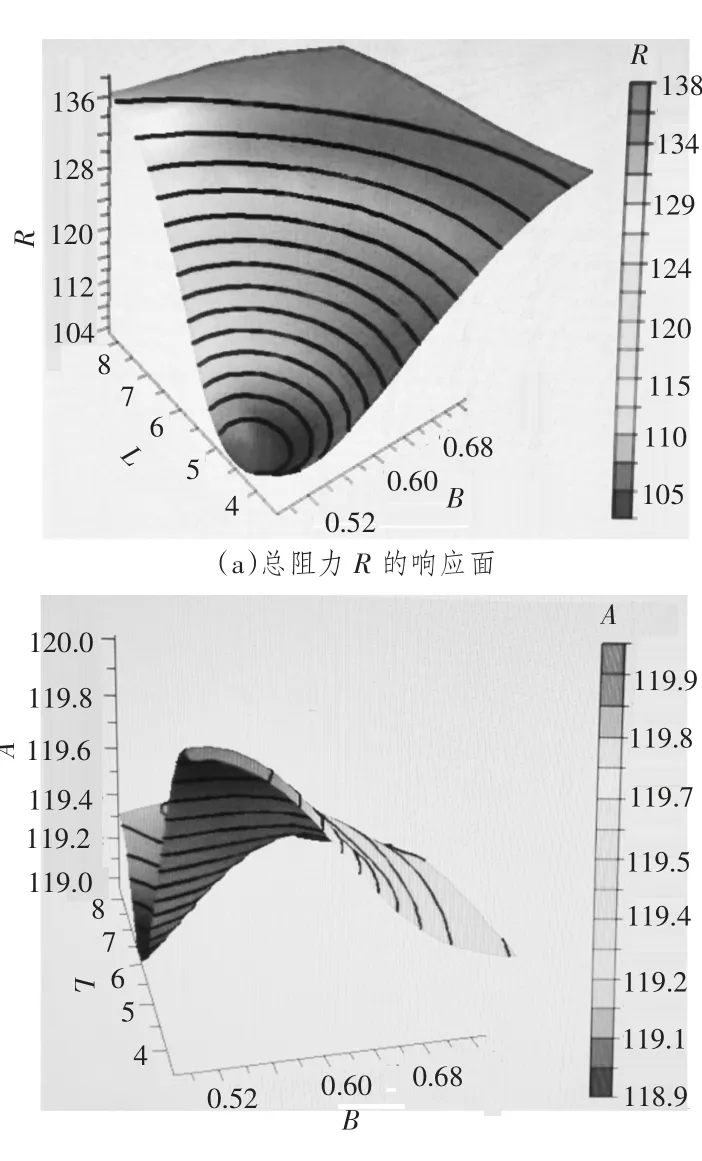
图4 总阻力R 及水动力噪声响应面Fig.4 The response of R and A
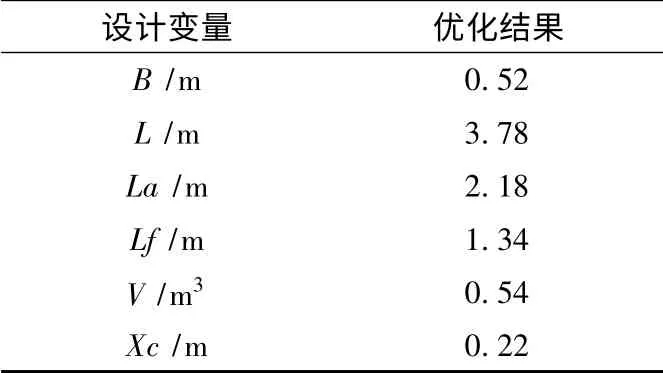
表2 最优的设计变量值Tab.2 The design variability on the best result

表3 优化结果值Tab.3 The best result
优化结果表明排水量较小的方案,在水动力噪声和快速性方面表现更好,这与目前舰船领域广泛开展的集成优化思路不谋而合,也从侧面应证了本方法的有效性。
3 结 语
本文所述的计算方法具有如下特点:
1)可形成子学科性能数据库,快速对子学科性能进行预报;
2)在子学科数据库足够充足的情况下,可实现线型的快速多学科优化。
本文所述的计算方法对于设计变量较多的水面舰船线型优化更具优势,对于舰船的总体设计和性能计算也具有指导意义。
[1]宋维保,李福新.回转体最小阻力外形优化设计[J].水动力学研究与进展,1994,9(5):23 -28.SONG Wei-bao,LI Fu-xin. The hull line optimization of revolution [J]. The Research and Development of Hydrodynamic,1994,9(5):23 -28.
[2]JANSON C E,LARSSON L. A method for the optimization of ship hulls from a resistance point of view[R]. Doktorsavhandlingar vid Chalmers TekniskaHogskola,1997,35.
[3]FUDGE D M,ZINGG D W. A CAD-free and a CAD-based geometry control of system for aerodynamic shape optimization[C]//43rd AIAA Aerospace Science Meeting and Exhibit,Reno,Nevada,2005.
[4]刘明静,李日杰,刘传云.数学艇型建模研究[J].舰船科学技术,2013,35(1):38 -41.
[5]SCCOTT P,DANE H,FRANCIS N. Hydrod-ynamic optimization of ship hull forms [J]. Applied Ocean Research,2001,23(6):337 -355.
[6]杜月中,闵建,郭字洲.流线型回转体外形设计综述与型线拟合[J].声学技术,2004,23(6):93 -100.DU Yue-zhong,MIN Jian,Guo Zi-zhou. A review and mathematical formation of shape design of streamlined bodies of revolution[J].Technical Acoustic,2004,23(6):93-100.
[7]CINDY C W. Steady and unsteady force and moment data on a DARPA2 Submarine[D].1999.
