多学科设计优化在舰船设计中的应用

张 辉

(中国舰船研究院，北京100192)

0 引 言

现代工程设计往往是一个包含多学科设计且不断优化的系统工程，但出于设计变量和设计约束的增加、设计问题非线性的增强，数值计算软件的应用以及学科之间的耦合作用，导致现代工程设计问题复杂程度和计算量的大大增加，且设计结果难以达到最优设计。为了解决设计过程中所面临的挑战，多学科设计优化方法被提出，并最先应用于航空设计领域。由于航空设计师应用多学科设计优化方法成功地解决了航空飞行器设计中存在的难题，使得多学科设计优化——这一新兴设计方法得到了工程界的广泛关注［1－3］。

舰船设计包含水动力学、结构力学、材料、能源与推进、总体布置、成本以及风险评估等学科，是一个涉及到多个学科的工程问题，属于典型的多学科设计优化问题。传统设计采用的是螺旋设计法，该法割裂了学科之间的相互影响，其设计结果的好坏往往决定于总设计师的经验。在传统设计过程中，每个学科领域的专家主要关心各自子系统的分析与设计，而未能充分探索其他学科对该子系统的影响。当各子系统完成优化设计后，将其优化结果组合到一起，通过总体设计专家的经验对各子系统设计结果进行协调，得到改进的总体设计方案，然后各学科领域的专家再根据新的总体设计方案进行新一轮的子系统设计，该螺旋式设计过程反复进行，直到最后满足设计要求。显然，在此调整过程中，专家根据经验和带有明显主观的判断起了很重要的作用，由此得到的设计结果往往只是满足设计要求的解，并非真正的整体最优解，从而导致总体性能和设计效率的下降。

为了更好挖掘舰船设计潜力，提高舰船总体性能，实现舰船最优设计，必须寻找一种新的设计方法代替螺旋设计法。通过众多其他工程领域成功设计案例的启示，消除传统螺旋设计方法的固有缺陷，将多学科设计优化引入舰船设计将具有极其广阔的发展空间和重要的工程意义。

1 多学科设计优化方法

目前，众多科研机构和专家学者对多学科设计优化进行了多种版本的定义，本文采用美国航空航天管理局Langley 研发中心的多学科分支机构对多学科设计优化的定义:多学科设计优化是一种通过充分探索和利用系统中相互作用的协同机制来设计复杂系统工程和子系统的方法论［4］。

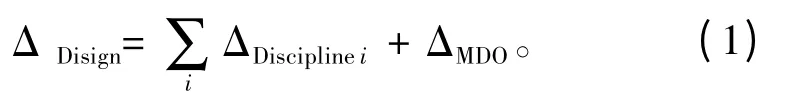
式中:ΔDisign为应用多学科优化设计后得到的总效益;为各个学科优化设计得到的效益和;ΔMDO为引入多学科设计优化所产生的效益，这里的关键即在于充分探索和挖掘学科之间的相关影响，实现优化设计，进而产生最大效益。

多学科设计优化的难点主要是计算代价和组织复杂性，这主要是因为:工程设计问题本身存在的大量设计变量以及为了使原设计问题解耦所引入的耦合变量，导致优化问题规模不断扩大，计算量大幅增加;多学科设计需要分解设计问题和组织管理各学科，故学科之间信息的相互交换和协调统一、数值分析软件的集成对接以及优化规模的合理控制将对减少计算量和成功实现优化设计具有极其重要的意义。

围绕以上两大难题，诞生了多种多学科设计优化方法:多学科可行方向法 (Multi － Disciplinary Feasible method，MDF;也称All －In －One，AIO)、同时分析和设计方法 (Simultaneous Analysis and Design;也称All － At － Once，AAO)、单学科可行方向法(Individual Discipline Feasible，IDF)、并行子空间优化方法(Concurrent Subspace Optimization，CSSO)、协同优化方法(Collaborative Optimization，CO)、两级系统综合方法［5－9］(Bi-Level Integrated System Synthesis，BLISS)。其中，MDF，AAO 以及IDF 属于单级多学科设计优化方法;CO，CSSO 以及BLISS 属于两级多学科设计优化方法。

经过10 多年的发展，国内多学科设计优化的研究从刚开始的全面借鉴到消化吸收，到完善发展，再到自主创新，取得了一些的成果。余雄庆开展了多学科设计优化方法及其在无人机设计中的应用研究;张勇等考虑舒适性与碰撞安全性，开展了汽车车身设计的多学科设计优化;操安喜等采用协同优化方法对潜艇实现了多学科设计优化;赵敏提出了两级集成系统协同优化方法(Bi － Level Integrated System Collaborative Optimization，简称BLISCO)［10－13］，实现了深海空间站的总体概念多学科设计优化。然而，水面舰船多学科设计优化的资料却比较少，潘彬彬等对国内某舰船实现了多学科设计优化，但学科仅限于快速性、操纵性和结构(船中剖面的总纵强度分析)，不能涵盖舰船的总体优化设计［14］;另外，2 篇［15－16］针对美国弗吉尼亚理工大学公布的巡洋舰CGX 设计模块进行的单级多学科设计优化，未能对多级多学科设计优化方法展开研究。本文主要采用该大学公布的导弹驱逐舰DDG 设计模块进行多学科设计优化，并对多级多学科设计优化方法的应用展开探索。

2 MDO 应用于DDG 设计

美国海军于1985 年至2005 年间采购DDG －51共计62 艘，由于成本等原因，美国海军计划将这些舰船的服役寿命由35 年增加至40 年，因此美国海军采用多学科设计优化方法在最大化军事效率的同时，实现后续舰船购置成本的最小化。该DDG 设计模块由美国弗吉尼亚理工大学［17］公布，共包含武备模块、推进模块、船型模块、舱容计算模块、电气模块、阻力模块、重量模块、液体箱容积模块、布置需要空间计算模块、可行性模块、经济性模块、军事效率模块、风险评估模块等13 个模块，总计25 个设计变量，如表1 所示。图1 给出了DDG 的设计结构矩阵，黑点表示有数据从左上方的学科向右下方的学科进行数据传递。通过该图可以发现，DDG 的设计有2 个特点:1)学科之间信息的大量交换，表明各学科之间存在着密切的联系;2)只存在设计

信息的向前传递，而没有信息反馈，表明DDG 的总体设计是一个顺序执行的过程。因此，DDG 的总体设计属于弱耦合设计问题。

表1 设计变量Tab.1 Design variables

续表1

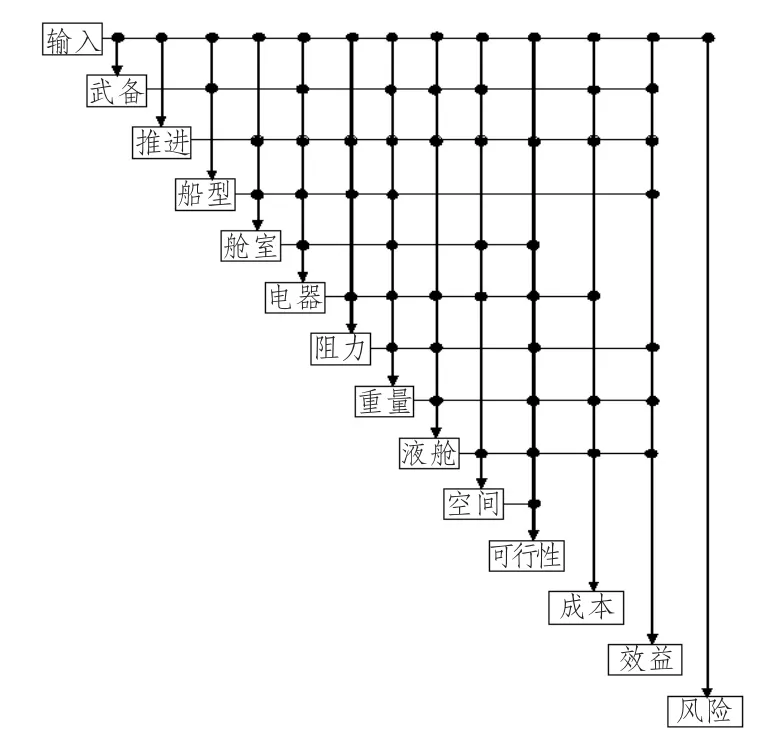
图1 DDG 系统集成模型的设计结构矩阵Fig.1 The design structure matrix of system synthesis model for DDG

由于计算条件的限制，以及本文着重演示多学科设计优化方法如何在DDG 设计上的实施，因此仅采用对DDG 设计有重要影响的8 个设计变量进行优化，它 们 分 别 是{LWL，B，T，D10，Cp，Cx，Crd，VD}。因 此，DDG 的多学科设计优化模型可以表示为如下形式:

优化算法采用基于Pareto 的多目标遗传算法(Multiple Objective General Algorithm，MOGA)，相应控制参数分别取为:群体规模20，最大进化代数100，杂交概率1，变异概率0.1。

以有军事效率最大化和后续舰船购置成本的最小化为设计目标，采用基于Pareto 的多目标遗传算法对DDG 的多学科分析模型进行优化计算，得到军事效率和后续舰船购置成本的Pareto 设计前沿，当运行至84 代时，达到收敛。第84 代时的DDG 多学科设计优化第84 代Pareto 设计前沿的优化结果和原始设计如表2 所示。

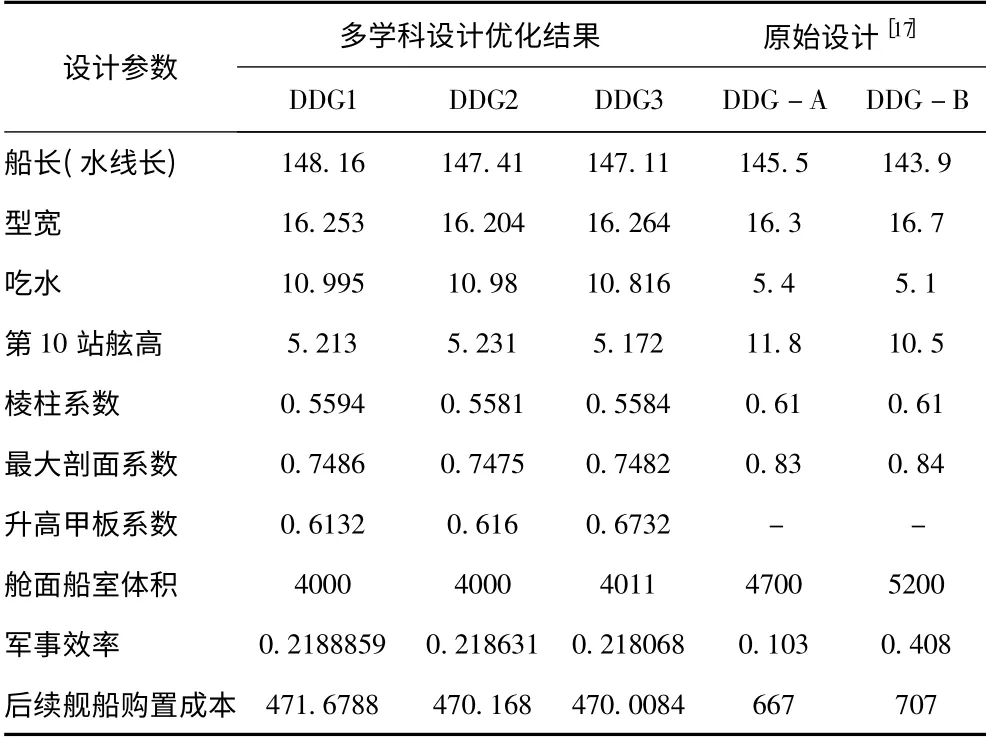
表2 DDG 多学科设计优化结果与原始设计Tab.2 The results of DDG with MDO and initial design

DDG 多学科设计优化所得到的Pareto 前沿均是一组优化解集，也称非支配解。可以看出当后续舰船购置成本越高时，军事效率也相应增加，反之，则随之降低。与文献［17］对比可以发现，DDG1、DDG2 和DDG3 的后续舰船购置成本均低于原始设计DDG－A 和DDG －B，且相应的军事效率高于原始设计DDG －A，小于DDG －B。因此，在提高军事效率的前提下，DDG1，DDG2 和DDG3 所需要的成本却小于DDG －A，说明DDG1，DDG2 和DDG3的设计优于DDG－A。

虽然通过上述MDF 方法实现了DDG 的多学科设计优化，但未能实现并行设计，导致效率较低。可以尝试采用协同优化(CO)方法，实现并行优化设计，达到提高计算效率的目的。对于协同优化在DDG 上的应用须进行一定的修改，因为DDG的设计包含13 个学科，如果直接将学科建立成相应的子系统，将导致系统级设计变量中出现大量的耦合设计变量，使得系统级优化规模不断扩大，产生计算困难。这里采用另一思路构建DDG 的CO模型。

系统级优化:将可行性、经济性、经济性以及风险评估这4 个模块纳入系统级，建立相应的优化模型。

子系统优化:

子系统1:将推进、电气、舱容计算、液体箱容积以及布置需要空间计算模块纳入子系统1;

子系统2:将武备和重量模块纳入子系统2;

子系统3:将船型和阻力模块纳入子系统3;

根据上述原则，建立DDG 的CO 模型如图2所示。

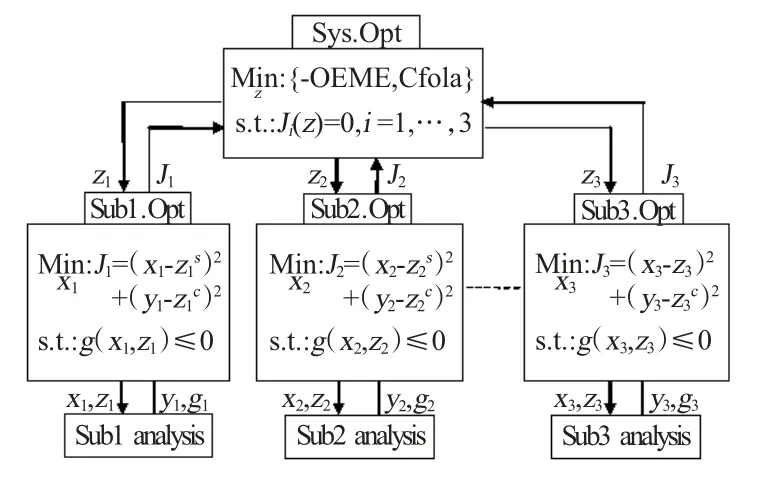
图2 DDG 协同优化框架Fig 2 The collaborative optimization framework for DDG

通过以上模型可以使得原有的串行单级多学科设计优化变为并行的两级多学科设计优化，这部分的工作将在后续阶段予以完成。

3 结 语

本文首先对舰船传统设计方法——螺旋设计法的主要缺点进行阐述，表明多学科设计优化方法对于舰船设计的重要意义，然后对多学科设计优化方法进行简要的综述。最后，围绕美国弗吉尼亚理工大学公布的导弹驱逐舰DDG 开展多学科设计优化，得到了DDG 设计目标军事效率和后续舰船购置成本的Pareto 前沿设计。该设计前沿显示军事效率的提高，将伴随后续舰船购置成本也上升，且本文得到的设计方案DDG1，DDG2 和DDG3 优于文献［17］所给的优化设计方案DDG －A。显然，通过引入多学科设计优化方法，DDG 的作战性能有所增加的同时，成本得到了降低，这对DDG 的总体设计是具有重要的工程价值和现实意义。此外，为了能更好提高设计效率，实现DDG 的并行设计，本文给出了DDG 的协同优化设计模型，这对将来实现DDG 的高效设计具有指导意义。

［1］KRASTEVA D T，BAKER C，WATSON L T，et al．Distributed control parallelism for multidisciplinary design of a high speed civil transport［C］// Proc．7th Symposium on the Frontiers of Massively Parallel Computation．Los Alamitos，CA，1999．

［2］KNILL D L，GIUNTA A A，BAKER C A，et al． Multidisciplinary HSCT design using response surface approximations of supersonic Euler aerodynamics［C］//Proc．36th Aerospace Sciences Meeting and Exhibit．Reno，NV，1998．

［3］MACMILLIN P E，GOLOVIDOV O，MASON W H，et al．An MDO investigation of the impact of practical constraints on an HSCT configuration ［C］// Proc． 35th Aerospace Sciences Meeting and Exhibit．Reno，NV，1997．

［4］KORTE J J，WESTONe R P，ZANG T A． Multidisciplinary optimization methods for preliminary design［C］// AGARD Interpanel (FDP + PEP)Symposium“Future Aerospace Technology in the Service of the Alliance”，Paris，NATO Research and Technology Organisation，1997．

［5］CRAMER E J，DENNIS J E，FRANK P D，et al． Problem formulation for multidisciplinary optimization［J］． SIAM Journal on Optimization，1994，4(4):754 －776．

［6］SOBIESCZANSKI-SOBIESKI J．Optimization by decomposition:A step from hierarchic to non －hierarchic systems［R］．NASA TM101494，1988．

［7］BRAUN R D．Collaborative optimization:an architecture for large-scale distributed design［D］． PhD Thesis，Stanford University，1996．

［8］SOBIESCZANSKI-SOBIESKI J，AGTE J S，SANDUSKY R R． Bi-level integrated system synthesis (BLISS)［R］．NASA TM－1998 －208715，1998．

［9］SOBIESZCZANSKI-SOBIESKI J，ALTUS T D，PHILLIPS M，et al．Bi-level integrated system synthesis for concurrent and distributed processing［C］// Proc． 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization．Atlanta，Georgia，2002．

［10］余雄庆，丁运亮．多学科设计优化算法及其在飞行器设计中应用［J］．航空学报，2000(1):2 －7．YU Xiong-qing，DING Yun-liang． Multidisciplinary design optimization a survey of Its algorithms and applications to aircraft design［J］． Acta Aeronautica et Astronautica Sinica，2000(1):2 －7．

［11］CAO An-xi，ZHAO Min，LIU Wei，et al． Application of multidisciplinary design optimization in the conceptual design of a submarine［J］． Journal of Ship Mechanics，2007，11(3):373 －382．

［12］张勇，李光耀，孙光永．汽车车身耐撞性与NVH 多学科设计优化研究［J］． 中国机械工程，2008，19(14):1760－1763．ZHANGh Yong，LI Guang-yao，SUN Guang-yong． Research on multidisciplinary design optimization of vehicle body crashworthiness and noise，vibration and harshness［J］．China Mechanical Engineering，2008，19 (14):1760－1763．

［13］ZHAO Min，CUI Wei-cheng．On the development of bi-level integrated system collaborative optimization ［J］．International Journal of Structural and Multidisciplinary Optimization，2011，43(1):73 －84．

［14］PAN Bin-bin，CUI Wei-cheng，LENG Wen-hao． Multidisciplinary design optimization of surface vessels［J］．Journal of Ship Mechanics，2009，13(3):378 －387．

［15］PAN Bin-bin，CUI Wei-cheng．Multidisciplinary design optimization methods for ship design［J］． Journal of Ship Mechanics，2008，12(6):914 －931．

［16］LIU Jun，YI Hong． Re-analysis of MDO for CGX example［J］．Journal of Ship Mechanics，2009，13(6):895 －904．

［17］STEPANCHICK E J，BROWN A J． Revisiting DDGX /DDG－ 51 Concept Exploration［R］． Virginia Polytechnic Institute and State University，2006．