水动力系数敏感性分析在潜艇水平面运动模型简化中的应用研究
2015-12-19李浪涛潘良高林俊兴
李浪涛,倪 刚,潘良高,胡 涛,林俊兴
(1.海军工程大学 动力工程学院,湖北 武汉430033;2.中国人民解放军92531 部队,海南 三亚572000;3.海军驻南京地区航天机电系统军事代表室,江苏 南京210006)
0 引 言
在潜艇操纵性研究中,计算机仿真作为操纵性预报最有前途的方法被广泛的使用[1]。目前,对潜艇操纵性进行评估的方法是基于传统的、以水动力系数表达水动力(矩)的水动力模型,通过时域的数值解算进而评估不同的机动[2]。模型中无因次水动力系数通常被认为是常数,该方法普遍用于预报潜艇水面、水下的操纵性及评估其运动控制性。而此方法的核心是仿真数学模型和水动力系数[3]。
通过大量的研究试验证明,用近似估算公式估算的水动力系数[4],来进行数值仿真预报潜艇操纵性的精度已经达到了工程要求[5]。但这种测算方法也有一些急需解决的问题:怎样进一步提高精度以及如何减少研究的工作量等。通过深入研究发现,不同的水动力系数对潜艇的操纵性影响范围和程度都有所不同,因此各水动力系数在模型中的重要程度也是不同的,如果可以找到各水动力系数对操纵性影响的规律,尽量提高对操纵运动影响显著的水动力系数的估算精度。同时将对操纵运动影响较小的水动力系数做较为粗糙的估算,或者将这些水动力从运动模型中舍去。这样不仅能够提高预报精度,而且可以大大减少工作量[6]。
因此,水动力系数敏感性研究提出了一个可以简化水动力模型和界定各水动力系数对潜艇操纵性影响程度的方法。本文采用水动力系数敏感性指数对某模型艇水平面运动模型的水动力系数敏感性进行了计算与分析,结果得到了不同水动力系数的相对重要程度,并且根据不同误差范围,简化了潜艇水平面动力模型。为潜艇的设计和操纵性研究提供参考,并为国家自然科学基金项目(51179196)的研究提供理论指导。
1 潜艇水平面运动模型
本文的坐标系、名词术语和符号,都采用国际水池会议(ITTC)推荐的和造船与轮机工程学会(SNAME)术语公报体系[2]。运动方程为潜艇标准水平面运动方程:
轴向运动方程:
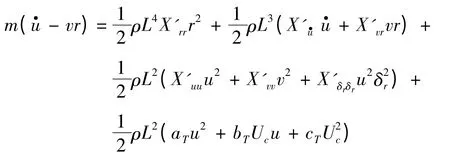
侧向运动方程:

转艏运动方程:
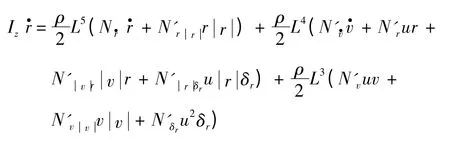
运动关系式:

从潜艇水平面运动模型看出,模型的确定需要2 个因素,一是反映模型结构的数学方程,二是描述潜艇的特征参数(水动力系数是特征参数之一)。当模型结构确定以后,潜艇的运动参数就构成了模型中参数的函数[6]。也可以说,潜艇水平面运动模型确定了一个从模型参数到运动参数的映射,这映射关系可以描述为:当给定模型参数的向量空间X 后,就决定了运动参数曲面R=S(X)。对向量空间X 中任意一个参数向量H,运动参数曲面S 上总有反映运动参数R 的一点P 与之对应,且P 点将随着H 的改变而改变。研究中发现,模型中任意参数的变化,都将引起运动参数R的改变。本文目的是研究潜艇在水平面回转运动中,模型参数空间中水动力系数的变化对战术回转直径的影响程度。
2 水动力系数敏感性指数
由于不同的水动力系数对于潜艇操纵性的影响程度不同,即潜艇操纵性对不同水动力系数的敏感程度不同,因此引入水动力系数敏感性指数S[7],定义如下:

式中:R 为运动参数,例如战术回转直径、超越深度等;H 为水动力系数。有上标* 为基准的水动力系数和对应仿真计算得到的运动参数,无上标为变化的水动力系数和对应仿真计算得到的运动参数。
从上式中可以看出,敏感性指数S 代表了潜艇在某一操纵条件下运动参数对水动力系数变化的敏感程度,可以理解为1%的水动力系数变化导致潜艇运动变化的百分点数。例如,在潜艇在航速8 kn、操方向舵5°进行水平面回转运动时,作为输入响应的某一水动力系数Hi变化a%,那么对于选取作为输出响应的战术回转直径,也会相应的变化b%,输出响应的变化比上输入相应的变化,即可以求出此操纵条件下作为运动参数的战术回转直径的水动力系数敏感性指数。当S = 0 为输入变化对输出响应没有任何影响;S >0 为输出响应随输入的增大而增大;S <0 为输出响应随输入的增大而减小。同时,S 的绝对值越大说明输入变化对输出响应的影响程度越大,即该水动力系数对操纵运动的影响越显著。
3 水动力系数敏感性指数计算与分析
3.1 水动力系数敏感性指数的计算
本文利用Matlab7.8/ Simulink 软件,根据某模型潜艇的结构特点和水动力系数,建立其水平面运动仿真模型。计算机模拟仿真其水平面回转运动,选取潜艇标准水平面运动模型中的27 个无因次水动力系数为输入量,输出响应为战术回转直径。因为回转运动试验是标准操纵试验,因此选择战术回转直径这个操纵性指数既可简化计算,又具有代表性,还可以较为全面反映潜艇的回转操纵特性[7]。本文在仿真试验过程中,只考虑单个输出响应与单个输入变量的敏感性。
在本文计算机仿真试验中,设定航速8 kn,分别操方向舵5°,10°,20°,30°,35°,每次通过选取单个水动力系数作为输入量,将其从-100%变化到+100%,每次变化20%,然后通过大量仿真计算得出相应的输出响应R。再根据敏感性指数公式计算出各操纵条件下、各输入量对应百分比变化的敏感性指数S 的值。本文将水动力系数的敏感性指数分类进行分析,做出具有代表性的水动力系数在各操纵状态下的敏感性指数曲线,各图中的横轴表示各水动力系数敏感性指数定义中纵轴表示图中各曲线的斜率为相应的敏感性指数。
各水动力系数分别在五种操舵运动状态下的敏感性计算结果,可以分3 类进行分析:1)如图1 所示水动力系数X′rr,此类水动力系数的敏感性指数在各舵角的运动状态下都为正,这种情况下各运动状态的战术直径随水动力系数的增大而增大。这样的系数包括2)如图2 所示水动力系数此类水动力系数的敏感性指数在各舵角的运动状态下都为负值,这种情况下各运动状态的战术直径随水动力系数的增大而减小,这样的系数包括δr;3)如图3 所示水动力系数X′vv,此类水动力系数的敏感性指数在各舵角的运动状态下有正值也有负值。这样的系数有X′u·,Y′r·,X′vv,Y′v·,N′v·,N′r·,bT,cT。
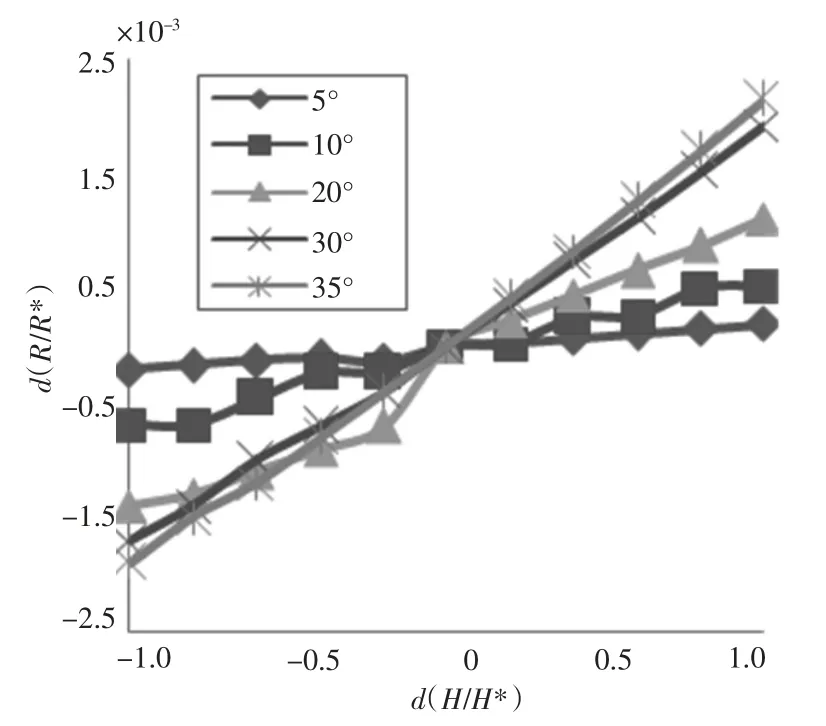
图1 在回转运动中的敏感性Fig.1 Sensibility of when submarine’s rotary movement

图2 在回转运动中的敏感性Fig.2 Sensibility of when submarine′s rotary movement
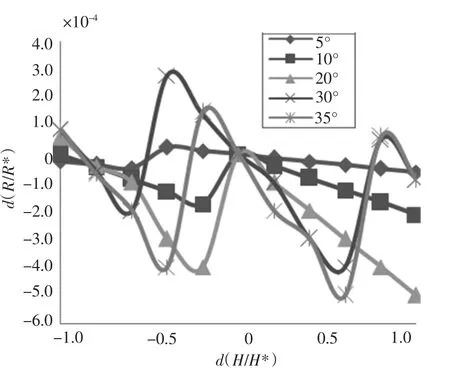
图3 在回转运动中的敏感性Fig.3 Sensibility of when submarine′s rotary movement
以上分析可知:在不同操舵运动状态下的各水动力系数敏感性指数存在很大差异。而在相同操舵运动状态下,各水动力系数敏感性指数也同样存在较大差异。本文以操舵20°为例,对相同操舵运动状态下的各水动力系数敏感性指数进行了分析,按水动力系数的性质分3 类进行分析:1)附加质量系数敏感性指数间的比较。从图4可知,在附加质量系数中,除外绝大多数附加质量系数在此运动状态下敏感性指数都很小;2)线性与非线性水动力系数敏感性指数之间的比较。对比分析图5 和图6 可知,无论是线性或是非线性系数,其中影响操纵性大的都是z 方向上的水动力力矩系数;3)不同方向上的水动力系数敏感性指数之间的比较。对比分析图7 ~图9可知,不管是哪个方向上的水动力 (矩)系数,对操纵性运动影响较大的都是与舵角有关的水动力系数。

图4 操舵20°时,附加质量敏感性曲线Fig.4 Sensibility curve of added mass when δr=20°
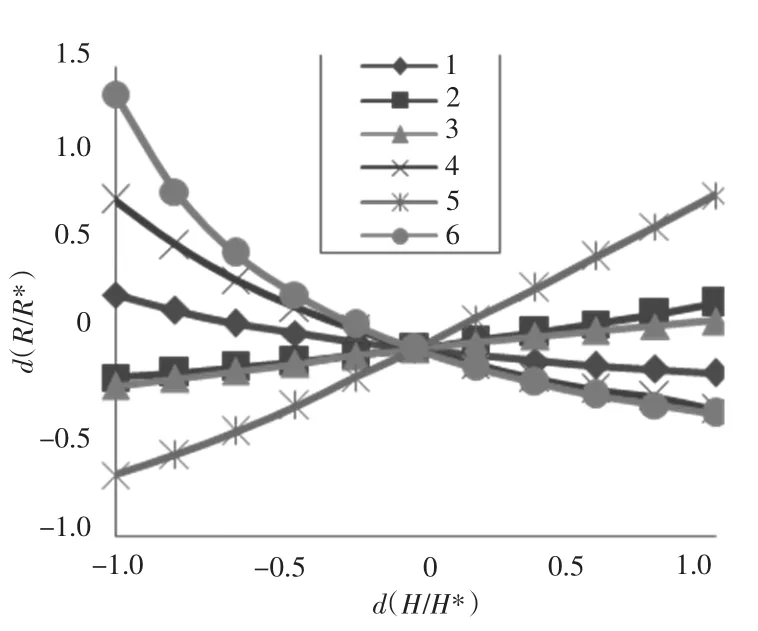
图5 操舵20°时,线性水动力系数敏感性曲线Fig.5 Sensibility curve of linear hydrodynamics coefficient when δr=20°
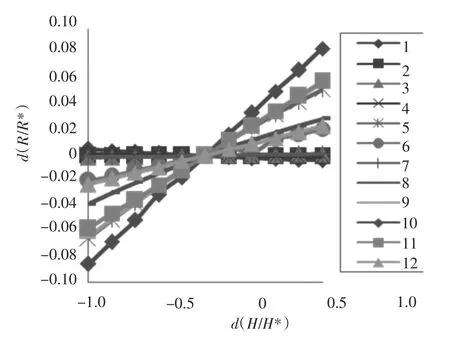
注:1—Xδrδr 2—Xrr 3—Xvr 4—Xvv
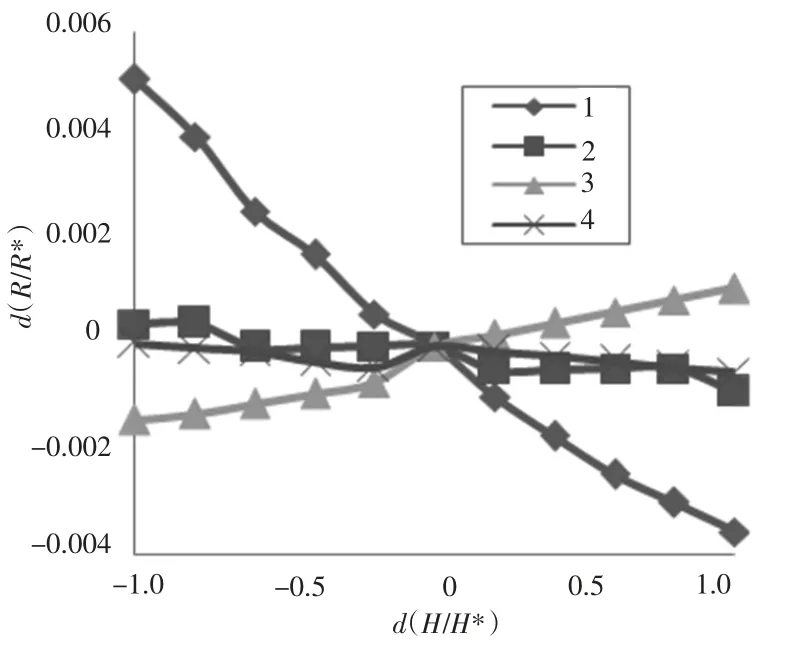
图7 操舵20°时,x 方向上水动力系数敏感性曲线Fig.7 Sensibility curve of hydrodynamics coefficient of x place when δr=20°

图8 操舵20 °时,y 方向上水动力系数敏感性曲线Fig.8 Sensibility curve of hydrodynamics coefficient of y place when δr=20°

图9 操舵20 °运动状态下z 方向上水动力系数敏感性曲线Fig.9 Sensibility curve of hydrodynamics coefficient of z place when δr=20°
3.2 水动力系数敏感性指数的确定
对于各水动力系数在不同操纵条件、不同变化输入量下的敏感性指数,选取其中绝对值最大者为本水动力系数在水平面回转运动下的敏感性指数,得到表1,其表征的是水动力系数对潜艇水平面回转运动状态下战术回转直径的最大影响程度。

表1 各水动力系数的最大敏感性指数Tab.1 The most sensitivity index of hydrodynamics coefficient
根据由表1 分析如下:不同水动力系数的敏感性指数是存在差异,即表明不同水动力系数对潜艇运动状态的影响程度不同;在该操纵条件下线性水动力系数的敏感性指数都大于非线性水动力系数的敏感性指数;转首力矩水动力系数的敏感性指数相对轴向力和侧向力水动力系数敏感性要大,这和回转运动特性相吻合。
通常情况下,我们感兴趣的只是其中敏感性指数较大的水动力系数,因为他们对相应的潜艇运动影响较大,为了更精确的预报潜艇运动,在估算或则试验计算这些水动力系数时,尽量提高它们的估算精度。而对于一些敏感性较小的水动力系数,由于它们对相应潜艇运动影响较小,所以我们可以根据自身的需要,为了减少工作量,对这些敏感性较小的水动力系数粗略估计或者舍去这些水动力项,从而简化模型。
3.3 模型简化与对比
本文分别选取了0.01,0.025,0.028,0.03,0.035,0.05 作为敏感性指数指标,将敏感性指数小于这些指标的水动力系数赋值为0,舍去敏感性较小水动力项,简化模型。其中,,aT,bT,cT这4 个系数为潜艇艇体结构自身所决定,故不能忽略;Y′r·和这2 个系数在模型计算过程中位于方程式分母位置,若忽略则运动方程无解,所以也不能赋值为0。所以,不同指标对应的可忽略水动力系数如表2。

表2 不同指标对应的可忽略的水动力系数Tab.2 The negligible hydrodynamics coefficient of various index
再次利用建立的运动仿真模型,对选择不同敏感性指数指标所简化的运动方程,在8 kn 航速下,分别操舵5°,10°,20°,30°,35°运动状态,仿真计算运动参数,绘制航迹线,并计算各模型在不同操纵条件下战术回转直径的误差值,如表3。这里列出在操方向舵5°时,取敏感性指数指标0.03 和0.05 下,简化的模型与原始模型仿真潜艇水平面回转运动的航迹曲线,如图10 所示。
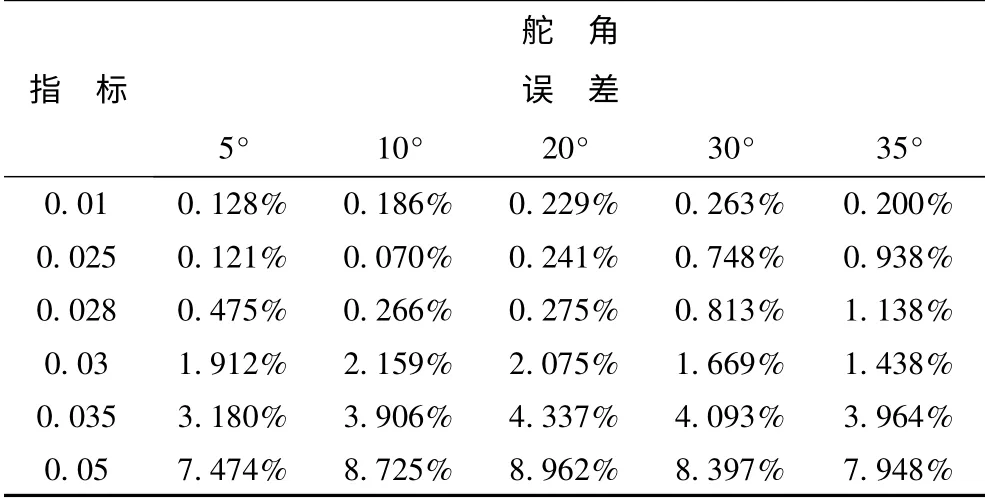
表3 不同敏感性指数指标下的战术回转直径相对原始模型战术回转直径误差Tab.3 Error of tactics rotary diameter of various index when new model compare with original model

图10 方向舵5°,取敏感性指数指标0.03 和0.05 简化的模型与原始模型仿真潜艇水平面回转运动航迹曲线Fig.10 The curve of simplified model and original model simulation submarine rotary movement in horizontal ,when δr=20°and sensitivity index of0. 03,0. 05
从图10 可知,简化方程后的仿真结果与原方程的仿真结果十分接近,很好的验证了水动力系数敏感性指数这种方法的有效性。并且从表3 可知,在同一操纵条件下,简化模型的误差值随着敏感性指数指标选取的增大而增大。所以,根据不同精度的需要,完全可以将方程进行不同程度的简化,以降低建模难度,减少运算量。
4 总结与展望
本文研究结果表明,根据计算的水动力系数敏感性指数,在潜艇设计和操纵性研究中,为了提高计算精度,可以对敏感性指数较大的水动力系数进行精确计算;为了减少工作量,在误差允许的范围内,可以对敏感性较小的水动力系数进行粗略估算或则舍去,从而简化模型。本文作为国家自然科学基金项目《基于高维全局分叉的水下航行器空间运动稳定性数值分析与自航模试验研究》 (51179196)研究的基础,为潜艇的操纵性和运动非线性研究提供了理论指导。
但是,本文主要以潜艇水平面运动模型,对单输出对应单输入来计算水动力系数的敏感性,没有考虑各水动力之间存在的耦合因素。根据项目的研究工作,接下来将对潜艇六自由度空间运动模型进行研究,并考虑各水动力系数之间存在的耦合因数,计算单输出对应多输入或则多输出对应多输入之间水动力系数的敏感性。
[1]陈厚泰. 潜艇操纵性[M]. 北京:国防工业出版社,1981.
[2]施生达.潜艇操纵性[M].北京:国防工业出版社,1995.
[3]王燕飞,朱军,张振山. 评估水动力系数对潜艇操纵性影响的一种方法[J].船舶力学.2005,9(5):61 -68.
[4]詹成胜,刘祖源,程细得. 潜艇水动力系数数值计算[J].船海工程,2008,37(3):1 -4.
[5]于东宾,周轶美,孙元泉. 关于回转机动时的横倾控制[J].船舶力学,1999(1):37 -43.
[6]刘杨.船舶操纵运动仿真中的水动力系数敏感性分析[D].哈尔滨:哈尔滨工程大学,2008.
[7]DEBABRATA S. A study on sensitivity of maneuverability performance on the hydrodynamic coefficients for submerged bodies[J].Journal of Ship Research,2000,44(3):186 -196.
[8]林俊兴,倪刚,戴余良,等.潜艇定常回转运动参数变化规律的研究[J].舰船科学技术,2014(1):31 -33.
[9]孙建刚,邓德衡,黄国樑. 水面船舶操纵性敏感性分析[J].中国航海,2006,66(1):49 -52.
[10]胡坤,徐亦凡,王树宗. 基于水动力系数敏感性指数的水下航行器运动方程简化研究[J].武汉理工大学学报(交通科学与工程版).2008,32(2):358 -361.
[11]倪刚,林俊兴.潜艇倒车倒航操纵性能分析[J].舰船科学技术,2012,34(10):41 -44.
[12]张晶.潜艇运动建模及简化技术研究[D].哈尔滨:哈尔滨工程大学,2009.
[13]徐锋,邹早建,尹建川,等.船舶操纵水动力导数的灵敏度分析[J].哈尔滨工程学报,2013,34(6):669 -673.
[14]刘勤贤,朱根兴,吕炜.潜艇回转运动模型建立与仿真[J].计算机测量与控制,2003,11(1):62 -64.
[15]林雄伟,胡大斌,戴余良. 潜艇非线性运动研究综述[J].船舶力学,2013,11(1):62 -64.
[16]陈宁,龚苏斌.船舶回转运动仿真[J].船舶力学,2013,53(3):9 -14.
