基于损失函数法的船舶操纵水动力导数灵敏度分析

方向红，徐 锋

(1.中国舰船研究院，北京100192;2.武汉第二船舶设计研究所，湖北 武汉430064)

0 引 言

船舶的水动力模型通常包含大量的水动力导数，这些导数对船舶的操纵运动建模及操纵性预报的影响权重相差很大，在保证预报精度的前提下，通过参数的灵敏度分析去除一些影响权重较小的水动力导数，可以降低模型的复杂度，提高运算效率;同时，模型中一些水动力导数，尤其是高阶非线性导数的物理意义并不明确，通过模型试验也很难得到这些导数，但从机理分析的角度并不能很好地对其进行简化，而灵敏度分析则可以解决这一问题。

另外，系统辨识加自航模试验或实尺度试验的方法被广泛应用于水面船舶操纵运动建模，而辨识建模的精度同水动力导数的灵敏度密切相关。Rhee和Kim［1］对水动力导数的灵敏度与其辨识精度的关系进行分析，指出灵敏度较大的水动力导数往往能够得到比较接近真值的估计值，而对模型贡献较小的参数一般很难得到。这一结果一方面可以用来解释辨识建模中一些水动力导数无法得到满意结果的原因，另一方面表明可以通过试验设计对各水动力导数的灵敏度值进行优化，以达到最佳辨识效果。

船舶操纵水动力导数的灵敏度分析是计算水动力导数变化所引起的船舶运动状态量的改变。换言之，灵敏度分析是计算船舶运动状态量相对于水动力导数的一阶偏导数。然而直接计算该偏导数难度较大，需要经过复杂的理论推导并借助于高级程序语言进行实现［2］。因此，通常使用的水动力导数灵敏度分析方法为间接方法，即不直接计算偏导数，而是使用船舶的操纵性指标或运动参数进行评价［3-5］。

本文拟采用灵敏度损失函数法，是间接方法的一种。与其他灵敏度分析方法相比，该方法计算简单且物理意义明确。通过计算灵敏度损失函数以确定水动力导数对整个操纵运动数学模型的影响权重，可直接得到各个水动力导数对船舶运动模型的权重因子，从而便于达成简化数学模型的目的。文中以Mariner 船为研究对象，通过15°/15°Z 形仿真试验，对Abkowitz 模型中包含的40 个粘性类水动力导数进行灵敏度分析，并对模型进行简化;然后，采用简化模型和原始模型进行25°/25°操纵运动仿真，通过2 种仿真结果的对比，对所提出的灵敏度分析方法进行验证。

1 船舶操纵运动数学模型

本文所使用的船舶运动模型为整体型船舶操纵运动数学模型，即Abkowitz 模型。原始Abokowitz 模型共包含5 个惯性类水动力导数和60 个粘性类水动力导数，根据Chislett 的试验结果，粘性类水动力导数被简化为40 个［6］。根据文献［7］中的无因次化模型可表示如下:

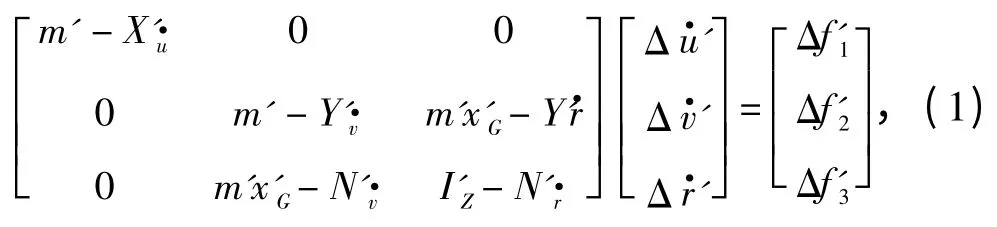
式中:上标‘′’代表该参数为无因次化参数;m 为船舶质量;Iz为关于z 轴的惯性矩;xG为船舶重心的纵向坐标;Δ，Δ和Δ分别为纵向加速度、横向加速度和转首角加速度;为惯性类水动力导数;Δf1，Δf2和Δf3分别为纵向水动力、横向水动力和转首水动力矩。其详细表达式如下:

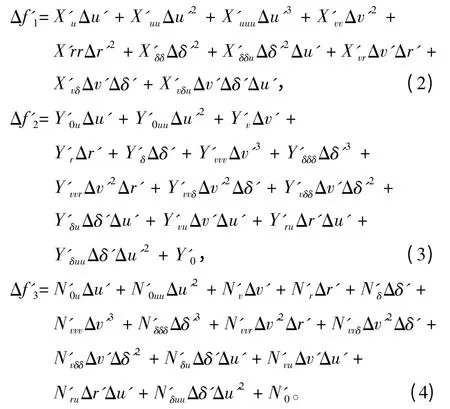
各水动力导数的因次转化关系可参考文献［8］。其他参数的因次转化如下:

式中:L 为船体长度;ρ 为海水密度;U 为合成速度。通常以船舶匀速直航时的运动状态作为基准，其速度设为u0，则各运动变量可计算如下:

其合成速度为:

2 损失函数法

基于损失函数法的灵敏度分析是根据船舶操纵运动仿真结果进行损失函数的计算，损失函数的计算结果即为灵敏度值。Perez 根据船舶四自由度数学模型定义了船舶横荡-摇首灵敏度损失函数和横摇损失函数［9］。横荡-摇首灵敏度损失函数如下:

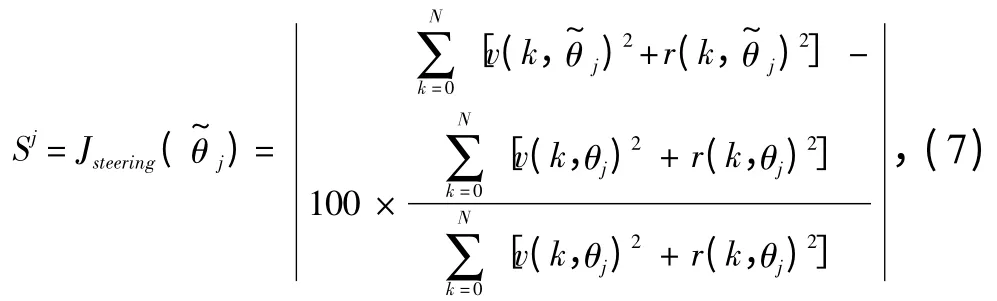
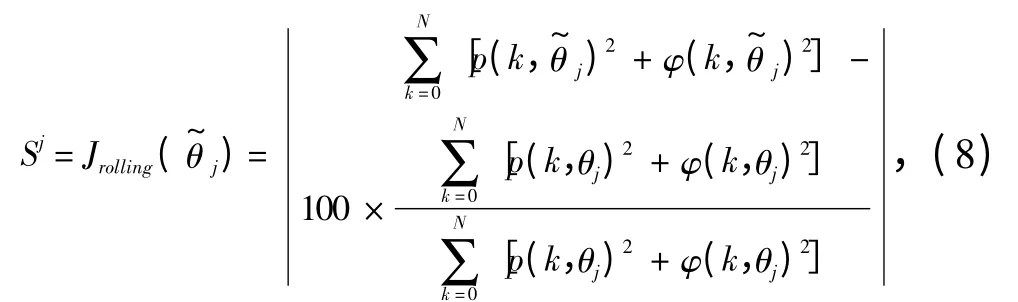
本文采用的纵荡-横荡-摇首三自由度灵敏度损失函数定义如下:

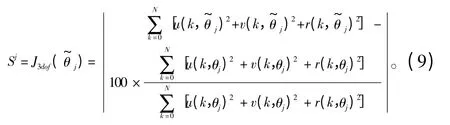
3 灵敏度分析结果

选取Mariner 船为研究对象，无因次化的水动力导数来源于文献［8］。在仿真中设采样间隔为0.5 s，样本数取为1 200，执行15°/15° Z 形仿真试验以计算各水动力导数的灵敏度损失函数。使用损失函数法进行灵敏度分析的详细流程为:

步骤1 使用文献［7］中的水动力导数进行15°/15°Z 形仿真试验，根据试验结果计算

步骤2 改变水动力导数X′u，令X′u= (1 +10%)X′u，保持其他水动力导数不变;

步骤3 进行15°/15°Z 形仿真试验，根据计算结果计算

步骤5 根据步骤2 ～步骤4，遍历所有水动力导数;

步骤6 将水动力导数的改变量依次变为-10%、+50%、-50%，重复步骤2 ～步骤5。

以水动力导数X′u为例，改变一定百分比后的操纵运动仿真对比如图1 所示。

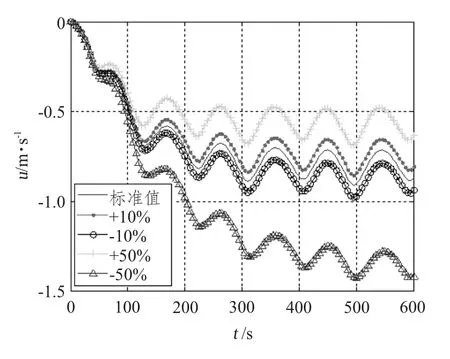
图1 X′u 改变后15°/15° Z 形试验中的纵向速度Fig.1 After The Change Of X′u，15°/15° Z′s Longitudinal Velocity In The Test

经过计算，可得到各个水动力导数的损失函数如表1 ～表3 所示。

表1 纵向水动力导数的灵敏度损失函数值后计算得到的灵敏度损失函数Tab.1 The Longitudinal Hydrodynamic Derivative Sensitivity Loss Function Value

表2 横向水动力导数的灵敏度损失函数Tab.2 The Horizontal Hydrodynamic Derivative Sensitivity Loss Function Value

表3 摇首水动力导数的灵敏度损失函数Tab.3 The Yaw Hydrodynamic Derivative Sensitivity Loss Function Value

从表1 ～表3 可发现:

1)对大部分水动力导数而言，改变+10%与-10%所计算得到的灵敏度损失函数值基本相同;改变+50%与-50%的情况与之相近，但差别相对较大;

2)水动力导数改变+50%、 -50%所得到的灵敏度损失函数值，基本相当于改变+10%、 -10%所得到的灵敏度损失函数值的5 倍;

3)各水动力导数的灵敏度值差别很大，部分水动力导数的灵敏度损失函数值近似为0，表明该水动力导数的改变对整个数学模型几乎没有影响;

为便于对各水动力导数的灵敏度进行分析，根据表1 ～表3 中的损失函数值和分析结果，采用式(10)对各水动力导数的平均损失函数值进行计算:

得到各水动力导数的平均损失函数值如表4 所示。

表4 水动力导数的平均灵敏度损失函数Tab.4 The Hydrodynamic Derivative Sensitivity On Average Loss Function Value

根据表4 定义水动力导数的取舍函数:

根据式(11)，可以把水动力导数简化至24 个，水动力导数可简化为0。

保持剩余的24 个水动力导数不变，即可得到简化的Abkowitz 模型。基于简化模型和包含所有水动力导数的原始模型，分别进行25°/25°Z 形仿真试验，其对比结果如图2 ～图3 所示。从图中可看出，模型简化后，各运动参数的改变很小，仍然能够精确地进行船舶操纵运动预报，这表明损失函数法进行船舶操纵水动力导数灵敏度分析可行。

图2 25°/25°Z 形仿真中纵向速度和横向速度时历曲线Fig.2 In 25°/25°Z Simulation The Curve Of Horizontal And Vertical Speed

图3 25°/25°Z 形仿真中摇首角速度、舵角和首摇角时历曲线Fig.3 In 25°/25°Z Simulation The Curve Of Yaw Angular Velocity、Rudder Angle And Yaw Angle

4 结 语

本文提出使用灵敏度损失函数法对船舶操纵水动力导数进行灵敏度分析，并对Abkowitz 模型进行简化。文中以Mariner 船为研究对象，基于15°/15°Z 形仿真计算得到了各水动力导数改变+10%， -10%，+ 50%， - 50% 后的损失函数值，通过定义平均损失函数值计算公式和取舍函数，将Abkowitz 模型中包含的40 个粘性类水动力导数简化至24 个。对比简化模型和原始模型的25°/25°Z 形仿真试验，表明损失函数法应用于船舶操纵水动力导数灵敏度分析的有效性。

［1］RHEE K P，KIM K. A new sea trial method for estimating hydrodynamic derivatives［J］. Ship ＆ Ocean Technology，1999，3(3):25 -44.

［2］徐锋，邹早建，尹建川，等，船舶操纵水动力导数的灵敏度分析［J］. 哈尔滨工程大学学报，2013，34(6):669 -673，715.

［3］SEN D.A study on sensitivity of maneuverability performance on the hydrodynamic coefficients for submerged bodies［J］.Journal of Ship Research，2000，44(3):186-196.

［4］HWANG W Y.Application of System Identification to Ship Maneuvering［D］.Ph.D. thesis，Massachusetts Institute of Technology，Cambridge，MA，1980.

［5］MISIAG W A，KOSE A. The sensitivity analysis of predicted maneuvering performance of full bodied ship in the case of MMG mathematical model［J］.Trans. West-Japan Society of Naval Architects，1994.

［6］CHISLETT M S，STROM-TEJSEN J.Planar motion mechanism tests and full-scale steering and maneuvering predictions for a Mariner class vessel［J］.International Shipbuilding Progress，1965，129(12):201-224.

［7］FOSSEN T I.Guidance and control of ocean vehicles［M］.John Wiley ＆ Sons，New York，1994.

［8］李殿璞. 船舶运动与建模［M］. 北京:国防工业出版社，2008.

［9］PEREZ T，BLANKE M. Mathematical ship modeling for control applications［R］.Technical Report，The University of Newcastle，Australia，2002.