螺旋桨/大柔性机翼静气动弹性快速分析方法

谢长川，张利娟，刘燚，杨超

(北京航空航天大学 航空科学与工程学院，北京100191)

超长航时的无人机，由于其续航能力的要求，加之燃料动力在低速中空或高高空时效率低的原因，这类飞机一般采用高效太阳能为电动螺旋桨提供动力以保障超长甚至永久续航能力.采用螺旋桨推进系统的高空超长航时无人机，一方面由于具有大展弦比、柔性大的特点，这类飞机在正常飞行情况下就会产生显著的弹性变形，几何非线性气动弹性问题突出［1］;另一方面，由于柔性机翼翼载荷较低，可以预见螺旋桨滑流对机翼的气动弹性将产生强烈干扰.

针对几何非线性气动弹性问题，Patil等［2-4］建立了考虑失速特性的梁式机翼模型，采用动力学线化方法研究了几何非线性效应对单独机翼静、动气动弹性行为的影响;谢长川等采用推广的片条理论［5-6］及三维升力线理论［7］对金属单梁式机翼进行了非线性静气动弹性变形计算，并采用线化方法预测了颤振临界速度，并通过风洞试验验证了计算;Palacios和Cesnik采用计算结构力学(CSD)与计算流体力学(CFD)耦合计算的方法研究了柔性机翼的非线性静气动弹性响应问题［8］.针对螺旋桨滑流问题，Prandtl等建立了叶素动量理论，对螺旋桨气动特性进行了较为合理的分析［9］;Weir将涡格法应用于螺旋桨滑流的分析，在无黏不可压定常流动假设下对螺旋桨滑流及其与机翼的相互干扰进行分析［10］;Agostinelli等采用叶素理论和CFD方法对螺旋桨诱导速度及载荷进行较为详尽的分析，并分析了螺旋桨滑流与机翼的气动干扰［11］.近些年国内外学者多采用“等效盘”模型或全桨叶建模的CFD方法对该问题进行研究［12-15］.从研究现状来看，针对柔性机翼几何非线性气动弹性研究中并未考虑螺旋桨滑流的影响，而针对螺旋桨滑流的研究又大多忽略了机翼的弹性;Christian的研究虽然考虑了机翼的柔性，但其计算依赖于大量来自CFD计算及风洞实验的数据，对于理论分析及工程设计的指导意义并不大;CFD方法虽然能够提供高精度的流场分析，但它不能提供桨叶攻角、滑流诱导速度等原理性的数据，而且计算效率低.因此适用于大变形的“螺旋桨/大柔性机翼”系统的气动弹性分析快速方法有待进一步研究.基于这种研究背景，本文提出了一种具有工程精度、适用于初步设计阶段的快速分析方法，为我国高空长航时无人机的研制做技术储备.

1 理论基础

1.1 螺旋桨滑流及“1P load”的分析方法

对于拉力螺旋桨构型的飞机，机翼的部分处于螺旋桨滑流区，螺旋桨滑流的切向速度分量在机翼上引起当地攻角的增大或减小从而在机翼上产生上洗区和下洗区;并且滑流轴向速度较之远前方来流增大，处于滑流区的机翼会感受到动压增加.这样螺旋桨滑流对机翼绕流就产生了干扰.反过来，机翼涡系又会在螺旋桨桨叶处诱导出下洗，也就是说螺旋桨与机翼的气动干扰是相互的.虽然螺旋桨与机翼间的干扰流场为复杂的非定常流动，但仅就静气动弹性分析，可忽略螺旋桨的交变载荷效应及机翼对螺旋桨的诱导作用［16］.

“1P load”是指螺旋桨桨盘面内载荷［17］.当气流沿螺旋桨轴线流动时，螺旋桨上产生拉力、反扭矩，其方向均沿着螺旋桨轴向.但是，当气流非对称流经螺旋桨桨盘时(如图1所示)，螺旋桨桨叶产生周期性的气动力变化，螺旋桨上的净载荷并不沿轴向，而包含螺旋桨桨盘面内的载荷，即“1P load”.准确地预测螺旋桨载荷对于结构设计十分重要:“1P load”会产生一个平均值，对机翼升力及扭转都有影响，同样地，这些变化的面内载荷会对结构疲劳造成很大的影响.

图1 螺旋桨叶素力和速度图Fig.1 Load and velocity diagram of blade element-momentum theory

1.1.1 Prandtl修正的叶素动量理论

本文基于Prandtl修正的叶素动量(BEM)理论对螺旋桨滑流进行分析.考虑螺旋桨非对称入流情况，将螺旋桨桨叶沿半径及方位角两个尺度离散，螺旋桨桨叶被分成若干个处于方位角ψ下的叶素，如图1所示，在螺旋桨局部坐标系Oxyz中，原点O位于桨盘中心，Ox轴沿螺旋桨安装轴向后，Oz轴在桨盘平面内向上，螺旋桨沿Ox轴正方向逆时针旋转为正转，反之为反转.

叶素处速度的轴向分量:

旋转速度分量:

设wa，wt分别为轴向诱导速度和旋转诱导速度，引入轴向速度诱导因子a和旋转速度诱导因子a′，即 wa=aV1，wt=a′V2.

根据动量定理可得叶素处拉力及扭矩为

根据叶素处气动力关系，求得该方位角下拉力与扭矩为

其中，B为桨叶数;c为叶素弦长;φ为气流相对叶素的入流角;Cn，Ct分别为拉力系数和扭力系数.

令方程(3)和方程(5)相等、方程(4)和方程(6)相等，并引入 Prandtl叶尖损失因子F［17］，那么可以得到诱导因子的表达式为

滑流区气流诱导速度是桨盘处气流诱导速度的2倍［9］.根据Prandtl修正的 BEM 理论计算得到的螺旋桨正转时滑流诱导速度分布见图2:轴向诱速在桨轴两侧对称分布，体现了滑流轴向加速的效果;旋转诱速的分布取决于螺旋桨的转向，在桨轴两侧反对称分布，图示为螺旋桨正转结果.

图2 螺旋桨滑流诱导速度分布图Fig.2 Figure of propeller slipstream’s induced velocities distribution

1.1.2 “1P load”的计算

关于“1P load”的研究还不深入，对其产生的原因、带来的影响可参考的文献极少.因此有必要对“1P load”的产生机理做简要的揭示.

如图1所示，以螺旋桨在桨盘平面内正转为例说明，气流以相对螺旋桨安装轴夹角α流过，则来流速度在 Oz轴正向有分量 V∞sinα.［0°，180°］方位角范围内称为前行桨叶区(因为气流相对桨叶的切向速度是桨叶旋转速度和V∞sinα之和)，而在［180°，360°］方位角范围内情况相反.

沿Oz方向的垂直面内载荷产生的原因容易揭示:相对于后行桨叶，前行桨叶有更大的气流攻角和流速，因此产生更大的升力、阻力，这两个力在旋转平面内的垂直分量较大，因此，整个螺旋桨面内的净载荷就是垂直向上的.沿Oy方向的水平面内载荷产生的机理并不是很直接，因为它基于复杂的非定常气动力，主导原因是诱导速度在桨盘平面内的变化.

如图1螺旋桨桨叶半径r处的任一叶素，其气流及气动力分布情况:dFt和dT分别为叶素切向力及垂直拉力的微分量.由几何关系，可以推导:

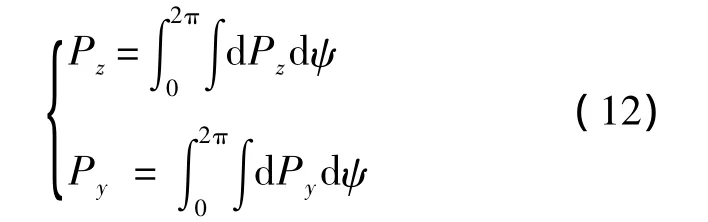
根据上述分析，求得在V∞=14 m/s，螺旋桨转速ns=135 r/s，αflight=5°时螺旋桨面内载荷在一个旋转周期随方位角的变化情况，如图3所示.

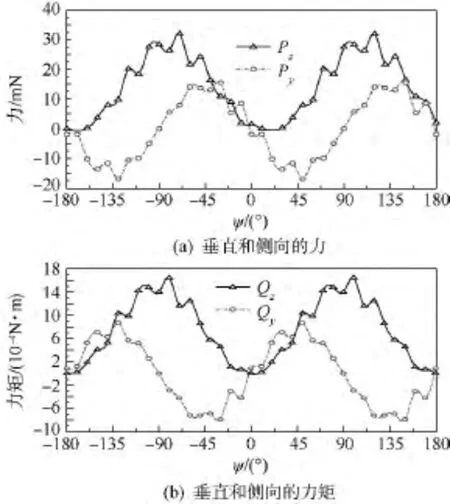
图3 “1P load”一周期内随方位角变化图Fig.3 1P force distribution vs azimuth angle

可见，沿y轴的载荷的平均值基本为0，而沿z轴方向的面内载荷有较大的平均值，是“1P load”的主要部分，这部分载荷不仅对机翼升力和扭转变形有贡献，并且这种交变载荷很可能会影响机翼的稳定性，在后续稳定性研究中应给予重视.图4给出沿z向的面内载荷随入流攻角的变化情况，随着入流攻角的增加，面内垂直载荷不断增加.

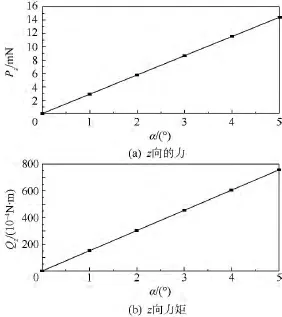
图4 “1P load”中z方向的载荷随飞行攻角变化图Fig.4 Vertical force and moment of“1P load”vs flight angle of attack

1.2 滑流对大柔性机翼诱导的模拟

虽然螺旋桨直径相对机翼展长只是一个小数，但螺旋桨滑流对整个机翼都有诱导效果.本文计算中简化认为滑流区为一个从桨盘向后拖出的以桨盘为底面的圆柱体.旋转的滑流会带动滑流区边界外的气流旋转，这样螺旋桨滑流就在整个机翼上诱导出下洗或上洗.处于滑流区内的机翼，其上的诱导速度已通过BEM理论计算得到;对于滑流区外的机翼，滑流的诱导作用，本文采用兰金(Rankine)涡核模型［18］模拟，如图5所示，螺旋桨滑流简化成一条由螺旋桨旋转中心向后延伸的一根有限涡段.根据工程估算经验，涡段长度可取为6倍机翼根弦长.根据毕奥-萨法尔定理，兰金涡核在滑流区外任一点的诱导速度为

其中，R为螺旋桨桨盘半径;r为诱导点到涡核轴线的距离;Γ为兰金涡核的涡强，由滑流旋转速度确定.

图5 Rankine涡对空间一点诱导示意图Fig.5 Geometry induced schematic diagram of the Rankine vortex

1.3 螺旋桨/大柔性机翼静气动弹性分析流程

针对大柔性机翼非线性气动弹性问题，前期研究工作可参考文献［19］.这里沿用对柔性机翼的非线性气弹分析方法，在此基础上加入螺旋桨推进装置，建立了“螺旋桨/大柔性机翼”系统的静气动弹性分析流程，如图6所示.通过BEM理论计算得到的螺旋桨滑流通过兰金涡作用到机翼的空间马蹄涡系上，接着根据三维升力线方法得到机翼载荷，将螺旋桨载荷及机翼载荷一并加载到结构有限元模型上，利用NASTRAN非线性静力分析，得到结构变形.根据结构变形更新模型的气动构型，并开始新一轮计算.迭代计算以机翼主梁翼尖的垂向变形为收敛条件，直到满足收敛条件则停止计算.

图6 螺旋桨/大柔性机翼静气动弹性分析流程图Fig.6 Flow chart for nonlinear static aeroelastic analysis of the propeller/wing system

2 算例分析

2.1 计算模型

以文献［19］中所用某单梁式柔性机翼的右半翼展模型为算例，运用本文所建立的几何非线性分析方法，对其在螺旋桨滑流作用下的静气动弹性进行分析.机翼外形如图7所示，具体参数见文献［19］.电机选为XM2815A，最大功率95 W，重20 g.螺旋桨选择5X5E，重4 g，两叶定距，桨叶翼型为NACA0016.螺旋桨安装在机翼主梁靠根部143.5 mm处向前伸出48 mm，螺旋桨及其安装轴材料的刚度很大，在结构分析中忽略螺旋桨部分的弹性效应.

图7 大柔性机翼模型结构示意图Fig.7 Structure of the very flexible rectangular wing

根据实际结构建立的结构非线性有限元模型如图8所示.机翼主梁刚度特性用梁单元模拟，质量特性用分散于翼面的多个集中质量模拟，螺旋桨系统简化为翼根刚性连接于主梁的短梁，电机质量以集中质量平均分配到短梁的3个节点上，螺旋桨质量加载于短梁前端点上.初始气动面模型如图9所示，沿展向按内翼段、滑流区、外翼段3部分共划分30个片条.

图8 模型初始有限元结构图Fig.8 Initial finite element model of the structure

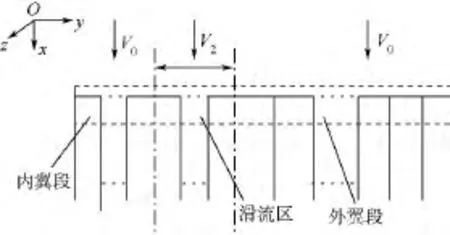
图9 模型初始气动构型图Fig.9 Initial aerodynamic model of the structure

2.2 几何非线性静气弹分析结果

下面具体讨论几何非线性计算情况下“螺旋桨/大柔性机翼”系统的静气动弹性特性，主要包括机翼气动特性和变形分布等情况.

2.2.1 螺旋桨滑流对机翼气动力的影响

图10给出了风速V=14 m/s，飞行攻角5°，螺旋桨正、反转(转速分别为 0，130，135，140 r/s)情况下，机翼根部固支约束，气动升力、诱导阻力、侧力沿机翼展向的分布图.当螺旋桨正转时，滑流在内侧机翼区诱导下洗，在外侧机翼区诱导上洗，使得内侧机翼有效攻角减小，外侧机翼有效攻角增加，内侧机翼气动力减小，外侧机翼气动力增加，当螺旋桨反转时，情况与之相反;侧力是气动升力沿片条侧向的分量，大小随升力而变化;另外，滑流区机翼动压的增加使得滑流区内升力显著增加.诱导阻力的分布形式主要取决于机翼气动片条的下洗角，是机翼涡系和滑流兰金涡线共同诱导的效果，在满足物面边界条件情况下，机翼的马蹄涡系分布发生变化，使下洗角分布呈“M”型，因此诱导阻力分布如图10(b)所示.为进一步说明，文中还给出了转速为135 r/s时气动模型各片条的兰金涡诱导攻角、马蹄涡诱导攻角、合成有效攻角的分布图，如图11所示.可见，绕流下洗角在滑流区受马蹄涡、滑流及动压增加的共同影响，在滑流区外主要受马蹄涡的影响.

图10 机翼气动力沿翼展分布图Fig.10 Distribution of aerodynamic force in the three orientations along wingspan

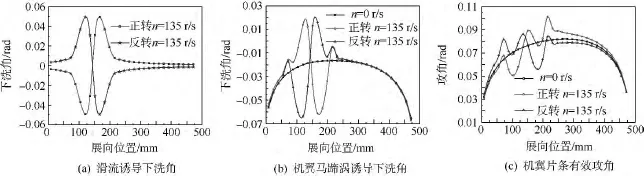
图11 气动片条攻角沿翼展变化图Fig.11 Distribution of strip’s attack angle distribution along the wingspan

2.2.2 螺旋桨滑流对机翼变形的影响

图12给出了相同计算情况下机翼主梁沿垂向、侧向及纵向的变形.在螺旋桨拉力、扭矩及机翼气动载荷、结构重力的共同作用下结构发生变形.当螺旋桨正转时，随着转速的增加，由于机翼气动升力、侧力的增加，机翼主梁沿垂向、侧向的变形显著增大.总的来说，在算例构型下，螺旋桨正转对机翼为气动加载，并且转速越大，升力增加的效果越明显;螺旋桨反转与此相反.而机翼沿纵向变形受气动阻力、螺旋桨拉力的共同影响，随着转速增加，螺旋桨拉力增大，在一定转速后，拉力增大程度使得螺旋桨安装处的机翼纵向向前变形.

图12 机翼主梁3个方向变形示意图Fig.12 Wing spar’s deformations in three orientations along wingspan

图13还给出螺旋桨转速135 r/s时，机翼主梁扭转变形情况.可见，螺旋桨正转还使得机翼扭转变形增大.螺旋桨转速越大，即前进比越小，螺旋桨拉力、扭矩及滑流均增强，对机翼气动力、变形的干扰作用越强.

图13 机翼主梁扭转Fig.13 Wing spar’s torsional deformation

由以上计算结果可见，螺旋桨滑流对机翼气动载荷有很大的干扰作用，使气动力在机翼上重新分布，进而影响结构变形特点;另外，螺旋桨转动引起的气动加载和减载效果，与螺旋桨的安装位置、旋转方向等因素有关，是一个多因素共同决定的结果.在工程应用中若不考虑螺旋桨滑流效应，势必会造成结构设计偏差，进而影响飞机的总体性能.因此，这一问题必须加以重视.

3 结论

1)螺旋桨在非对称入流条件下会产生桨盘面内载荷，其中沿桨盘垂直向上的载荷为主要载荷，它对机翼升力、扭转变形及结构稳定性都有影响，应该在设计初期就给予足够重视.

2)由算例结果知，拉力螺旋桨在机翼流场中增加了一个螺旋涡并增加了机翼当地来流动压，对柔性机翼静气弹特性产生影响，对机翼纵向变形的影响主要取决于螺旋桨载荷，而对机翼气动力、垂向及展向变形的影响主要取决于螺旋桨滑流.

3)螺旋桨对柔性机翼的弹性扭转、气动力分布、翼尖位移和扭转角等均产生较大的影响，使机翼的几何非线性效应更加显著，对机翼的性能造成了一定影响，需要在设计初期就给予重视.

References)

［1］ 谢长川，杨超.大展弦比飞机的几何非线性气弹问题［C］//第七届全国空气弹性学术交流会论文集.北京:中国空气动力学会，2001:97-102.Xie C C，Yang C.Geometric nonlinear static aeroelasticity problems of high-aspect-ratio planes［C］//7th National Conference on Aeroelastic Academic Communication.Beijing:Aerodynamic Society of China，2001:97-102(in Chinese).

［2］ Patil M J，Hodges D H.On the importance of aerodynamic and structural nonlinearities in aeroelastic behavior of high-aspect-ratio wings，AIAA-2000-1448［R］.Altanta:AIAA，2000.

［3］ Patil M J，Hodges D H，Cesnik C E S，et al.Limit cycle oscillations in high-aspect-ratio wings［C］//40th Structures Structural Dynamics，and Materials Conferernce and Exhibit.St.Louis:AIAA，1999，3:2184-2194.

［4］ Patil M J，Hodges D H，Cesnik C E S.Characterizing the effects of geometrical nonlinearities on aeroelastic behavior of high-aspect-ratio wings［C］//International Forum on Aeroelasticity and Structural Dynamics.Williamsburg，VA:［s.n.］，1999:501-510.

［5］ 谢长川.飞行器气动弹性稳定性静/动耦合理论与试验研究［D］.北京:北京航空航天大学，2009.Xie C C.Static/dynamic coupling theory and test study of aircraft aeroelastic stability［D］.Beijing:Beihang University，2009(in Chinese).

［6］ Xie C C，Leng J Z，Yang C.Geometrical nonlinear aeroelastic stability analysis of a composite high-aspect-ratio wing［J］.Shock and Vibration，2008，15(3-4):325-333.

［7］ 刘燚，谢长川.大展弦比机翼的几何非线性静气动弹性分析方法［C］//第十二届全国空气弹性学术交流会会议论文集.北京:中国空气动力学会，2011:227-233.Liu Y，Xie C C.Anlysis method for geometric nonlinear static aeroelasticity of high-aspect-ratio wings［C］//12th National Conference on Aeroelastic Academic Communication.Beijing:Aerodynamic Society of China，2011:227-233(in Chinese).

［8］ Palacios R，Cesnik C E S.Nonlinear aeroelastic modeling and experiments of flexible wings，AIAA-2006-2186［R］.Newport:AIAA，2006.

［9］ 刘沛清.空气螺旋桨理论及其应用［M］.北京:北京航空航天大学出版社，2006:56-63.Liu P Q.Air propeller theory and application［M］.Beijing:Beihang University Press，2006:56-63(in Chinese).

［10］ Weir D S.Wing loads induced by a propeller wake，AIAA-86-1967［R］.Seattle:AIAA，1986.

［11］ Agostinelli C，Liu C H，Allen C B，et al.Propeller-flexible wing interaction using rapid computational methods，AIAA-2013-2418［R］.San Diego:AIAA，2013.

［12］ 段中喆，刘沛清，屈秋林.某轻载螺旋桨滑流区三维流场特性数值研究［J］.控制工程，2012，19(5):836-841.Duan Z Z，Liu P Q，Qu Q L.Numerical research on 3-D flow field characteristics within the slipstream of a low loaded propeller［J］.Control Engineering of China，2012，19(5):836-841(in Chinese).

［13］ 鄂秦，杨国伟，李凤蔚，等.螺旋桨滑流对飞机气动特性影响的数值分析［J］.西北工业大学学报，1997，15(4):511-516.E Q，Yang G W.Li F W，et al.On coupling effect of two vortex systems of Chinese aircraft with turbo-propellers［J］.Journal of Northwestern Polytechnical University，1997，15(4):511-516(in Chinese).

［14］ 左岁寒，杨永.螺旋桨滑流对带后缘襟翼机翼气动特性影响的数值分析［J］.航空计算技术，2007，17(1):54-57.Zuo S H，Yang Y.Numercal simulation of propeller/high-lift system interaction［J］.Aeronautical Computing Technique，2007，17(1):54-57(in Chinese).

［15］ 段义乾，史爱明.一种新型的螺旋桨滑流激励盘模型的研究方法［J］.西北工业大学学报，2012，30(6):841-846.Duan Y Q，Shi A M.A new and effective actuator disk model approach for the simulation of propeller slipstream［J］.Journal of Northwestern Polytechnical University，2012，30(6):841-846(in Chinese).

［16］ Kroo I.Propeller-wing integration for minimum induced loss［J］.Journal of Aircraft，1986，23(7):561-565.

［17］ Ortun B，Boisard R.In-plane airloads of a propeller with inflow angle:prediction vs experiment，AIAA-2012-2778［R］.New Orleans:AIAA，2012.

［18］ 黄国伟.非定常漩涡空气东流额理论及应用［M］.上海:上海交通大学出版社，1994:56-61.Huang G W.Unsteady vortex aerodynamics theory and application［M］.Shanghai:Shanghai Jiao Tong Unversity Press，1994:56-61(in Chinese).

［19］ Xie C C.Theoretic analysis and experiment on aeroelasticity of very flexible wing［J］.Science China，2012，55(9):2489-2500.