蜂蝇悬停和前飞时的动稳定性
2015-12-19许娜孙茂
许娜,孙茂
(北京航空航天大学 航空科学与工程学院,北京100191)
近年来,随着对昆虫飞行空气动力学机理的深入研究和认识,人们将目光更多地转移到飞行动稳定性的研究上来[1-12].昆虫飞行中的扰动运动包括纵向和横向两种,通过对运动方程的线化处理,可将二者分开进行研究.对于昆虫悬停的纵向稳定性的研究,目前已经做了大量的研究工作[1,3,6,8,11].近年来,运用类似于纵向稳定性的处理方法,人们对昆虫的横向稳定性[9-11]也进行了一定的研究.通过对不同种类昆虫稳定性的研究,昆虫悬停时纵向和横向稳定性已较为清楚,但昆虫在前飞状态下的稳定性研究较少;区别于悬停状态,昆虫在前飞时有自由来流,拍动平面倾角相对较大,翅膀在下拍时的攻角和相对速度与上拍时也有很大的不同.前飞和悬停在平衡状态下运动参数的差异有可能导致二者气动导数的不同,从而出现不同的稳定特性.文献[7,12]分别研究了熊蜂前飞时纵向和横向的稳定性,总结并分析了其与悬停时动稳定性的差异.而到目前为止,由于前飞数据缺乏的局限,昆虫前飞的稳定性问题只有上述针对熊蜂开展的研究,其普适性也亟待验证.因此,其他种类昆虫前飞时的纵横向动稳定性的研究工作仍具有重要意义.
本文选用具有相对完整前飞数据的蜂蝇为研究对象,应用平均模型理论和CFD方法计算其气动导数,并运用特征模态分析方法研究蜂蝇悬停和前飞时的纵向和横向动稳定性.
1 理论模型及计算方法
1.1 运动方程
参照文献[1,3,6],本文采用平均模型理论:将昆虫看作一个6自由度的刚体,并利用拍动周期内的平均气动力和气动力矩来代替翅膀的拍动作用,从而昆虫的运动方程可简化为类似于传统飞机的运动方程.
为方便描述昆虫的运动,引入固联于地面的惯性系Oexeyeze和右手体轴系Oxyz(见图1).体轴系原点O位于昆虫的质心;平衡飞行状态下,x轴和y轴分布在水平面内,x轴指向前方,y轴指向身体的右侧(见图1).昆虫运动各状态变量定义如下:沿3个体轴方向(x,y,z)的速度分量分别为 u,v,w;绕3 个体轴(x,y,z)转动的角速度分别为p(滚转角速度),q(俯仰角速度)和r(偏航角速度);x轴与水平面的夹角为θ(俯仰角),y轴和水平面的夹角为γ(滚转角).
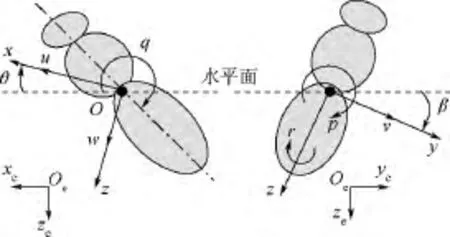
图1 各状态变量定义及坐标系示意图Fig.1 Definition of state variables and sketches of reference frame
昆虫的总质量记作m;重力加速度记作g;绕x轴、y轴和z轴的转动惯量分别记作Ix,Iy和Iz,惯性积记作Ixz.X,Y和Z分别为拍动周期内平均气动力沿x轴、y轴和z轴的分量;L,M和N分别为绕x轴、y轴和z轴的平均气动力矩.昆虫的身体运动可近似看作是由稳定的、对称的平衡状态量(以下标e表示)和一系列小的扰动分量(以前缀符号δ表示)组成,假设平衡飞行状态下,ve=we=pe=qe=re=θe=γe=0,前飞速度记作 ue;并且 Xe=Ye=Le=Me=Ne=0,Ze= -mg.在此基础上对运动方程进行线化,将纵向和横向运动解耦,对二者分开进行研究(见文献[13]).线化后的纵向与横向运动方程如下:
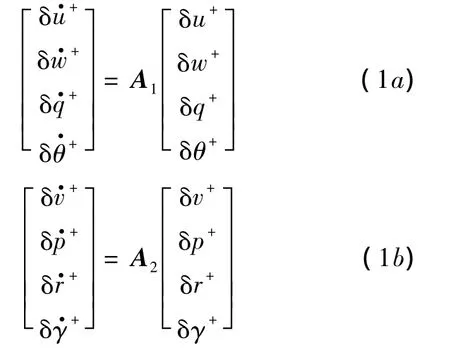
其中A1和A2分别为纵向运动和横向运动的稳定性矩阵:

其中 Xu,Zu,Mu,Yv,Lv,Nv等为昆虫运动纵向和横向稳定性气动导数.方程(1)和方程(2)中各量均已无量纲化:
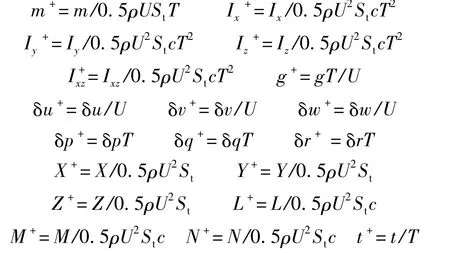
其中,St为两个翅膀的面积;参考速度U为翅膀的平均拍动速度(U=2Φnr2,Φ为拍动幅度,n为拍动频率,r2为翅膀面积二阶矩折合半径);参考长度c为翅膀平均弦长;参考时间T为拍动周期(T=1/n).
本文采用的蜂蝇模型主要形态学参数如下(蜂蝇运动学和形态学参数均由加州大学伯克利分校Robert Dudley教授提供):身体质量m=145 mg;单个翅膀的质量 mwg=0.326 mg;翅长R=11.2 mm;翅膀平均弦长 c=3.246 mm;翅膀面积二阶矩折合半径r2=0.534R;翅根与翅膀质心间距离 r1,m=0.38R;单个翅膀面积 S=36 mm2;体长lb=1.29R;两翅根间距离为0.33lb;翅根轴与身体质心间距离l1=0.13lb;自由悬挂时身体的角度 χ0=53.3°;本文采用与文献[9]中相同的方法估算蜂蝇的转动惯量和惯性积,悬停和各前飞速度下相应的估计值见表1.至此,纵横向系统矩阵A1和A2中只差相应的气动导数未知.
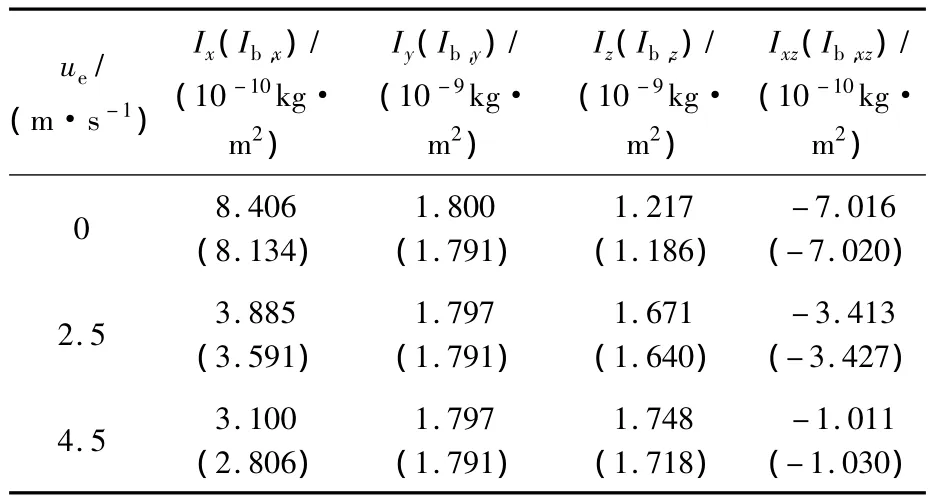
表1 蜂蝇悬停和前飞时相应的转动惯量和惯性积Table1 Moments and product of inertia of dronefly at hovering and forward flight
1.2 N-S方程求解与气动导数计算
1.2.1 翅膀和身体的运动
本文所用蜂蝇翅膀平面形状(如图2(a)所示)取自文献[14],模型翅近似为刚性平板,厚度为平均弦长的3%,前后缘为圆弧.身体模型的外形轮廓如图2(b)所示.
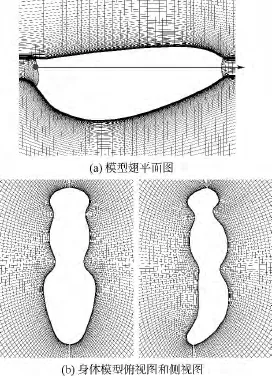
图2 蜂蝇的翅膀与身体模型Fig.2 Model of a dronefly’s wing and body
悬停和前飞时身体模型的速度(飞行速度ue)和姿态(身体角度χ)定义如图3(a)所示.
为方便描述模型翅的拍动,引入坐标系O1x1y1z1,其坐标原点O1位于翅根,x1y1平面与翅膀拍动平面重合,见图3(b).模型翅的拍动有两个自由度:一个为绕O1z1轴的转动,转角记为φ,即翅膀的拍动角;另一个为绕翅膀展向轴的转动,转角记为α,即是翅膀的攻角.拍动角φ随时间的变化可近似表示为
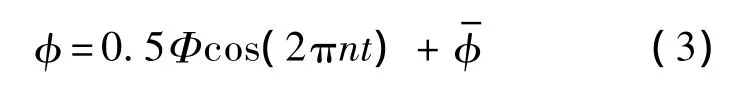
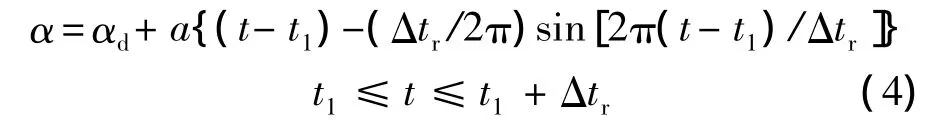
其中,Δtr为翅膀的翻转时间;a为常数;t1为翅膀开始翻转的时刻:
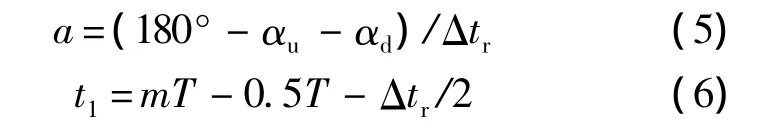
T为翅膀拍动周期.翅膀的下翻运动可用同样的方式描述.从方程(3)~方程(6)可以看出,为了描述翅膀的拍动,需确定以下参数:Φ,n,Δtr,αd,αu和.为描述拍动平面,还需给出拍动平面倾角β.
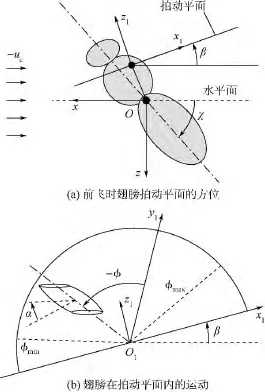
图3 模型翅运动及坐标示意图Fig.3 Sketches of reference frames of wing motion
所需运动参数 Ф,n,Δtr,β 和 χ列于表2,Δtr在悬停和前飞下均为0.30T;前进比定义为J=ue/2nΦR.
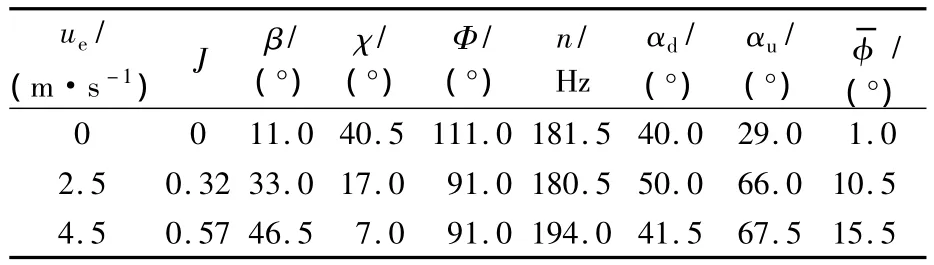
表2 蜂蝇悬停和前飞的运动学参数Table2 Kinematic parameters of dronefly at hovering and forward flight
由于αd和αu的实验数据存在较大的测量误差,而且气动力矩对于的变化也较为敏感,因此,本文通过力和力矩的平衡条件确定αd,αu和:翅膀和身体的平均垂直力之和需平衡昆虫的体重;翅膀的平均水平力需等于身体的阻力;翅膀和身体对于质心的俯仰力矩之和需等于0.雷诺数Re大小约为948(Re定义:Re=Uc/ν,其中,ν为运动黏度系数,U和c定义如上).
1.2.2 N-S 方程求解
要获得气动导数,首先需确定悬停和各前飞速度的平衡状态.平衡状态的确定和气动导数的计算均需数值求解N-S方程.N-S方程数值求解过程在文献[15-16]中已有较为详尽的描述,此处不再赘述.本文使用的计算程序已多次在先前的悬停研究中验证和使用过(例如文献[9,15]),前飞计算中只是在远场边界加入来流速度,而来流速度等于昆虫的前飞速度.文献[17]研究结果显示左翅和右翅之间的干扰除了在进行“打开和合拢”运动时都可以忽略不计;文献[18-19]也证实了翅膀和身体间的干扰也较小,可以忽略.因而,绕翅膀和身体的流动可分别进行计算.
计算所用翅膀网格为100×101×107(法向×周向×展向)的O-H型网格,如图2(a)所示.壁面网格法向间距为0.0015c;远场边界约为20c.无量纲时间步长取0.02(以c/U进行无量纲化).基于文献[16]中对网格密度、时间步长以及算法和程序的验证,其工作表明,本文使用的数值计算方法是可靠的,各计算参数的选取也是合适的.
身体网格为80×81×95(沿身体模型截面的法向方向×周向方向×身体体轴方向)的O-O型网格,如图2(b)所示.计算所得身体的升力和阻力与实验测量结果进行了比较,计算值与实验测量值的差别基本在昆虫体重的2%以内,也就是说身体计算模型和真实身体实验结果间的差别对平衡飞行影响很小.
1.2.3 气动导数的计算
本文计算气动导数方法与文献[6]中纵向稳定性问题的研究方法相同.以纵向气动导数Xu,Zu和Mu(u-系列)计算为例,即在平衡状态的基础上,保持w,q,θ和飞行速度不变(w,q和 θ为0,飞行速度为ue),调整u可计算得一系列气动力和力矩(X,Z和M)随u的变化曲线,曲线在平衡点处的导数就是对应的气动导数.类似地,还可得到其他纵向气动导数w-系列和q-系列以及横向气动导数v-系列、p-系列和r-系列.
在确定气动导数的基础上,本文采用与文献[6]中纵向动稳定性研究类似的特征值和特征向量方法,方法概述详见文献[13].
2 结果与讨论
2.1 悬停和前飞的平衡条件及气动导数
根据力和力矩的平衡条件,通过求解拍动翅和身体的绕流,确定出蜂蝇悬停和各前飞速度下αd,αu和(见表2).在平衡状态的基础上,分别调整纵向状态变量u,w和q得到相应的气动力(X+和Z+)和气动力矩(M+);调整横向状态变量v,p和r得到相应的气动力(Y+)和气动力矩(L+和 N+).以前飞(J=0.32)为例,纵向和横向计算结果见图4(其他飞行状态结果类似).由图4可以看出,在 -0.15≤Δu+,Δw+,Δq+≤0.15 范围内,ΔX+,ΔZ+和 ΔM+相对于 Δu+,Δw+和 Δq+的变化线性较好;由图5可以看出,在-0.15≤Δv+,Δp+和 Δr+≤0.15 范围内,ΔY+,ΔL+和 ΔN+相对于Δv+,Δp+和Δr+的变化线性也较好,这意味着对昆虫运动方程的小扰动线化处理是合理的.
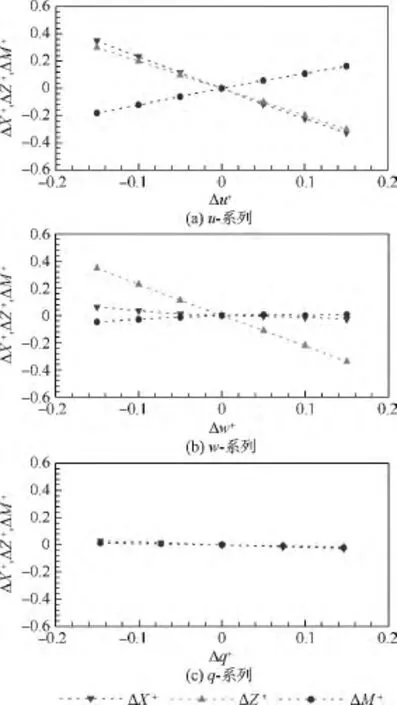
图4 蜂蝇前飞(J=0.32)时纵向u-系列,w-系列,q-系列无量纲气动力和力矩Fig.4 The u-series,w-series,q-series non-dimensional force and moment data at J=0.32
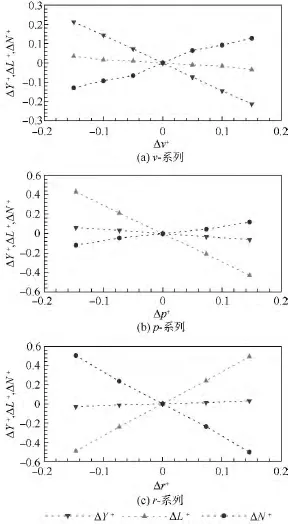
图5 蜂蝇前飞(J=0.32)时横向v-系列、p-系列、r-系列无量纲气动力和力矩Fig.5 The v-series,p-series,r-series non-dimensional force and moment data at J=0.32
根据图4和图5计算结果,可分别得到蜂蝇悬停和前飞平衡位置处的纵向和横向气动导数,见表3和表4.总的来说,相对于翅膀的气动导数,蜂蝇身体部分贡献较小.
首先考虑蜂蝇的纵向运动,由表3可以看出,悬停时(J=0),Xu+为负,Mu+为正,并且二者的绝对值比Zu+大得多,这表明蜂蝇的前后平移将产生与运动相反的阻力,向前运动时产生抬头的力矩,反之产生低头的力矩.Zw+为负且绝对值大于Xw+和Mw+,表明蜂蝇的上下运动将产生与运动方向相反的阻力.蜂蝇的俯仰运动产生的气动导数(Xq+,Zq+和Mq+)数值均较小.与悬停相比,蜂蝇前飞时的纵向运动除产生了与悬停类似的较大的气动导数Xu+,Mu+,Zw+外,导数 Zu+的绝对值也增大至与Xu+和Mu+相同的量级.
对蜂蝇的横向运动而言,由表4可见,悬停时(J=0),Yv+为负,Lv+为正,而且二者的绝对值比Nv+大得多,这表明昆虫的侧向运动(v+)主要产生一个与运动方向相反的侧向力(阻尼力)和一个与运动方向一致的滚转力矩(称Yv+为阻尼力导数,Lv+为侧滑滚转力矩导数).Lp+为负且其绝对值比Yp+和Np+大得多,表明昆虫的滚转运动(p+)主要产生一个较大的阻尼力矩.类似的,Nr+为负且绝对值较Lr+和Yr+大得多,表明昆虫的偏航运动(r+)也是主要产生一个阻尼力矩.因此,悬停时昆虫的横向扰动运动主要产生一个侧滑滚转力矩(Lv+Δv+)和3个阻尼力和力矩:包括一个侧向阻尼力(Yv+Δv+),一个滚转阻尼力矩(Lp+Δp+)和一个偏航阻尼力矩(Nr+Δr+).
与悬停相比,蜂蝇前飞时,Lv+的符号发生变化,变为负值;阻尼力和力矩导数(Yv+,Lp+和Nr+)绝对值进一步增大;偏航滚转力矩导数(Lr+)变化也较为显著,达到与阻尼力矩导数(Nr+)同等量级.这意味着,蜂蝇前飞时,其横向扰动运动产生了一个与运动方向相反的滚转力矩(Lv+Δv+),侧向阻尼力(Yv+Δv+)、滚转阻尼力矩(Lp+Δp+)和偏航阻尼力矩(Nr+Δr+)均增大;而偏航运动也可产生一个与阻尼力矩(Nr+Δr+)相当的滚转力矩.
2.2 特征模态和稳定特性
计算得到气动导数之后,方程(2)中系统矩阵A1和A2中各元素均可确定.应用特征模态的分析方法求解方程(2)可进一步分析蜂蝇的纵向和横向动稳定性.应用MATLAB软件分别计算系统矩阵A1和A2可得相应的特征值和特征向量.A1和A2的特征值计算结果分别见表5和表6.

表3 纵向气动导数Table3 Longitudinal aerodynamic derivatives

表4 横向气动导数Table4 Lateral aerodynamic derivatives
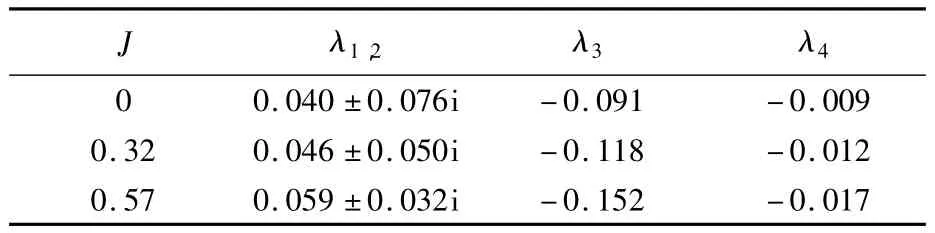
表5 蜂蝇悬停和前飞时纵向稳定性矩阵特征值Table5 Eigenvalues of longitudinal system matrix of dronefly at hovering and forward flight

表6 蜂蝇悬停和前飞时横向稳定性矩阵特征值Table6 Eigenvalues of lateral system matrix of dronefly at hovering and forward flight
蜂蝇的悬停和前飞纵向运动均存在一对实部为正的复数特征值 λ1,2和两个负的实特征值 λ3和λ4,这意味着蜂蝇的纵向运动由不稳定振荡模态、快衰减模态和慢衰减模态3个特征模态构成.悬停的结果与文献[3,6]对若干种昆虫的纵向稳定性研究类似.
本文所考虑的2种前飞速度的纵向特征模态结构上与悬停相同;表面上来看,这与熊蜂前飞[7]时的结果有所不同(熊蜂悬停和低速前飞时由不稳定振荡模态、快衰减模态和慢衰减模态构成;中等速度前飞时由2个振荡模态组成;较高的前飞速度由4个单调模态组成).但是,由表5可以看出,随着飞行速度的增大,蜂蝇纵向稳定性矩阵的复数特征值的实部在逐渐增大,意味着其不稳定性在逐渐增强,这种发展的趋势是与熊蜂的前飞纵向稳定性研究结果[7]一致的.与熊蜂最大前飞速度相比,蜂蝇高速前飞(J=0.57)时未出现4个实特征值的原因主要在于气动导数M+w较小.将前飞(J=0.57)时 M+w人为增大约1倍(M+w=0.60),系统矩阵A1中其他变量不变,可得特征值:λ1=0.132,λ2= - 0.196,λ3= -0.015,λ4=0.027;这种特征值的结构与熊蜂最大前飞速度的结果类似[7].在较大的前飞速度下,Mw+对熊蜂的纵向稳定性有着重要作用,且身体部分对其贡献占主要部分[7];而蜂蝇前飞时,身体部分对气动导数的贡献相对熊蜂要小,这可能是由于两种昆虫身体的外形差异引起的.
对于横向运动而言,悬停(J=0)时,存在一个正的实特征值λ1,一对实部为负的复数特征值λ2,3和一个负的实特征值λ4.它们分别代表了不稳定发散模态、稳定振荡衰减模态和稳定的衰减模态.这与文献[9,12]中悬停的横向稳定性结果一致.
前飞时蜂蝇横向运动系统矩阵的特征值结构与悬停(J=0)类似,但是特征值λ1随着飞行速度的增大而明显减小(前飞J=0.57时λ1=0);相应地,其横向运动的不稳定性在逐渐减弱;尤其是大前飞速度下(J=0.57),λ1=0,可视其为一种中性的稳定.蜂蝇前飞时这种横向运动的稳定性变化趋势与文献[12]中熊蜂前飞的研究结果也是一致的.
特征模态中,振荡模态的周期T和扰动增长倍幅期tdouble或扰动衰减的半衰期thalf可以更为直观地显示蜂蝇稳定性变化的趋势,相应的计算公式[13]如下:


表7 纵向特征模态的时间常数Table7 Time constant of longitudinal natural modes

表8 横向特征模态的时间常数Table8 Time constant of lateral natural modes
由表7可见,悬停时纵向运动的不稳定发散模态倍幅期tdouble≈17.3T,即初始扰动将在约17个拍动周期后幅值加倍;随着前飞速度的增大,不稳定发散模态的倍幅期tdouble在逐渐减小,也就是说初始扰动幅值加倍所需的时间在逐渐缩短,纵向运动的不稳定性即在逐渐地增强.
由表8可以看出,蜂蝇悬停时横向不稳定发散模态的倍幅期tdouble≈8.6T,而前飞时相应的倍幅期在逐渐增大(J=0.32时约为43T,J=0.57时趋于无穷大),即前飞时横向扰动的发散增长需要相对较长的时间,这也更直观地说明了蜂蝇前飞时横向的不稳定性在逐渐减弱;基于较长的倍幅期数值,可以将蜂蝇前飞的横向运动看作较弱或中性稳定.
运动各模态对应的特征向量决定了模态对应各状态变量的相位关系和幅值的相对大小.表9和表10分别给出了纵向和横向各特征模态对应特征向量的极坐标形式;由于特征向量的模可以为任意大小,而方向是唯一确定的,因此纵向和横向的结果分别用角度量δθ和δλ将特征向量归一化.
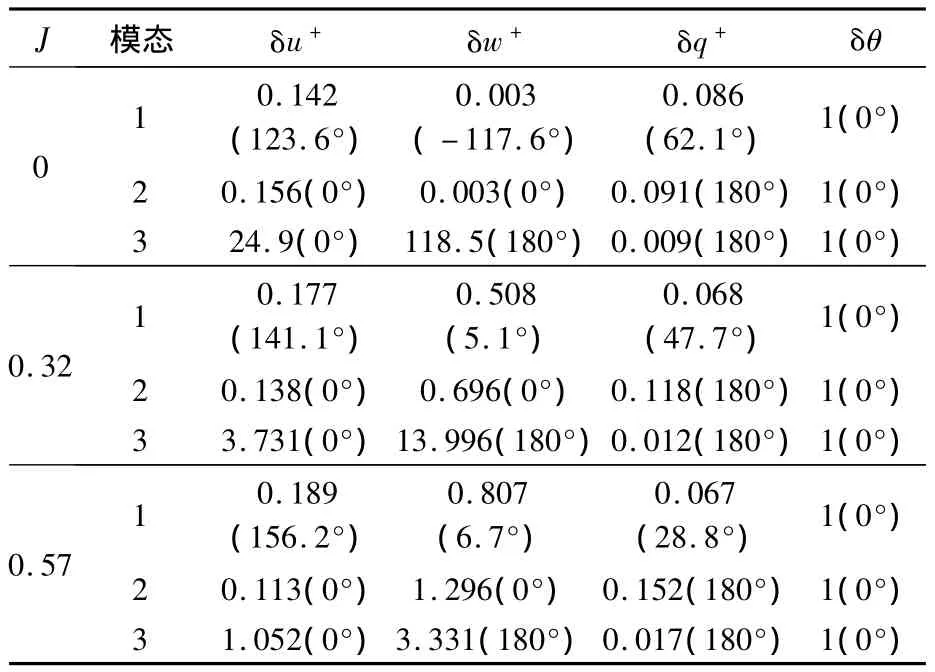
表9 蜂蝇悬停和前飞时纵向各模态对应的特征向量Table9 Eigenvectors of longitudinal natural modes of dronefly at hovering and forward flight
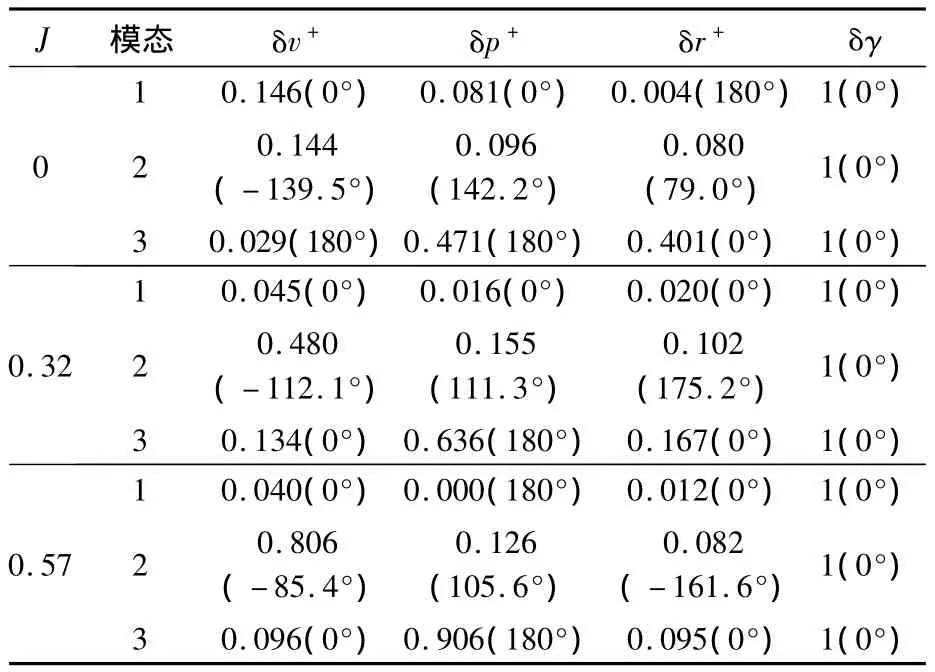
表10 蜂蝇悬停和前飞时横向各模态对应的特征向量Table10 Eigenvectors of lateral natural modes of dronefly at hovering and forward flight
由表9和表10可分别看出纵向和横向各特征模态所对应的运动,具体阐释见早前悬停和前飞的研究工作[3,7,9].
3 结论
1)蜂蝇悬停时纵向扰动运动由不稳定振荡模态、快衰减模态和慢衰减模态构成;横向扰动运动由不稳定发散模态、稳定振荡衰减模态和稳定的衰减模态构成.蜂蝇纵横向运动中均有不稳定模态存在,表明其悬停是不稳定的.
2)蜂蝇前飞时的纵向扰动特征模态结构与悬停时相同,但其不稳定发散模态的倍幅期tdouble随着前飞速度的增加逐渐减小,这意味着初始扰动幅值加倍的时间在逐渐缩短,即蜂蝇前飞时纵向不稳定性在逐渐增强,对飞行不利.
3)蜂蝇前飞时的横向运动由于气动导数L+v的变化(由正变负),代表其不稳定模态的特征值逐渐减小至零,不稳定发散模态的倍幅期不断增大,这意味着前飞时蜂蝇的横向不稳定性较悬停不断减弱,趋于一种中性的稳定.
4)尽管蜂蝇前飞时横向的不稳定在逐渐减弱,但其飞行稳定性包括纵向和横向两方面,而前飞时纵向的不稳定性在逐渐增强,因此,总体上来说,蜂蝇的前飞也是不稳定的.
References)
[1] Taylor G K,Thomas A L R.Dynamic flight stability in the desert locust Schistocerca gregaria[J].Journal of Experimental Biology,2003,206(16):2803-2829.
[2] Schenato L,Wu W C,Sastry S.Attitude control for a micromechanical flying insect via sensor output feedback[J].IEEE Transactions on Robotics and Automation,2004,20(1):93-106.
[3] Sun M,Xiong Y.Dynamic flight stability of a hovering bumblebee[J].Journal of Experimental Biology,2005,208:447-459.
[4] Deng X,Schenato L,Wu W C,et al.Flapping flight for biomimetic robotic insects,part I:system modeling[J].IEEE Transactions on Robotics,2006,22(4):776-788.
[5] Liu H,Nakata T,Gao N,et al.Micro air vehicle-motivated computational biomechanics in bio-flights:aerodynamics,flight dynamics and maneuvering stability[J].Acta Mechanica Sinica,2010,26(6):863-879.
[6] Sun M,Wang J K,Xiong Y.Dynamic flight stability of hovering insects[J].Acta Mechanica Sinica,2007,23(3):231-246.
[7] Xiong Y,Sun M.Dynamic flight stability of a bumblebee in forward flight[J].Acta Mechanica Sinica,2008,24(1):25-36.
[8] Faruque I,Humbert J S.Dipteran insect flight dynamics,part 1:longitudinal motion about hover[J].Journal of Theoretical Biology,2010,264(2):538-552.
[9] Zhang Y L,Sun M.Dynamic flight stability of a hovering model insect:lateral motion[J].Acta Mechanica Sinica,2010,26(2):175-190.
[10] Faruque I,Humbert J S.Dipteran insect flight dynamics,part 2:lateral-directional motion about hover[J].Journal of Theoretical Biology,2010,265(3):306-313.
[11] Cheng B,Deng X Y.Translational and rotational damping of flapping flight and its dynamics and stability at hovering[J].IEEE Transactions on Robotics,2011,27(5):849-864.
[12] Xu N,Sun M.Lateral dynamic flight stability of a model bumblebee in hovering and forward flight[J].Journal of Theoretical Biology,2013,319:102-115.
[13] Etkin B,Reid L D.Dynamics of flight:stability and control[M].New York:Wiley,1996.
[14] Ellington C P.The aerodynamics of hovering insect flight.II.morphological parameters[J].Philosophical Transactions of the Royal Society of London,Series B:Biological Sciences,1984,305(1122):17-40.
[15] Sun M,Tang J.Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J].Journal of Experimental Biology,2002,205(1):55-70.
[16] Wu J H,Sun M.Unsteady aerodynamic forces of a flapping wing[J].Journal of Experimental Biology,2004,207(7):1137-1150.
[17] Sun M,Yu X.Aerodynamic force generation in hovering flight in a tiny insect[J].AIAA Journal,2006,44(7):1532-1540.
[18] Yu X,Sun M.A computational study of the wing-wing and wing-body interactions of a model insect[J].Acta Mechanica Sinica,2009,25(4):421-431.
[19] Liang B,Sun M.Aerodynamic interactions between contralateral wings and between wings and body of a model insect at hovering and small speed motions[J].Chinese Journal of Aeronautics,2011,24(4):396-409.
