基于连续蚁群算法的Bayesian方位估计快速方法

焦亚萌，黄建国，韩晶

(1.西安工程大学 电子信息学院，西安710048;2.西北工业大学 航海学院，西安710072)

子空间类方法相对传统的高分辨方法而言具有较高的分辨性能，在高信噪比条件下对空间相邻的两目标源的分辨能力能够达到波束宽度的1/3～1/5［1］.但这些方法是以子空间分析为基础的，系统误差带来的子空间扰动等原因均会使分辨性能急剧恶化［2-4］，贝叶斯高分辨方位估计方法为阵列高分辨方位估计开辟了新的途径，利用信号和噪声参数的联合后验概率密度函数对信号进行谱估计［5-6］，根据贝叶斯定理，把待估计量视为随机变量，引入被估计量的先验知识，从而提高了估计精度，改善了估计性能［7-8］.但该方法由于多重积分和多维搜索，理论复杂，计算量大，实时性差，难以实时应用.1992年，Dorigo提出的蚁群优化(ACO)算法［9-10］在旅行商问题(TSP)、模糊控制、调度问题以及车辆路径规划(VRP)等方面，取得了一系列较好的实验结果［11-14］.文献［15］用ACO算法解决加权子空间拟合算法的多维非线性搜索问题，得到了优良的高分辨性能.本文提出了一种基于ACO算法的Bayesian方位估计(ACO-Bayesian)快速方法，该方法对小夹角目标估计精度高，与Bayesian方法性能基本相同，收敛性好且计算量小，更易于实际应用.

1 Bayesian高分辨方位估计方法

假设阵列为均匀线列阵，M个阵元，阵元间距为d，K个远场窄带信号源分别以 θk(k=1，2，…，K)的入射角和频率f到达阵列的各个阵元.

信号可以是相干或非相干的，设阵列接收到的加性噪声为平稳的、零均值的高斯空间白噪声，方差为σ2.相邻阵元间的时延为τk=dsin θk/C(C为声速)，则第m个阵元在tn时刻的输出为

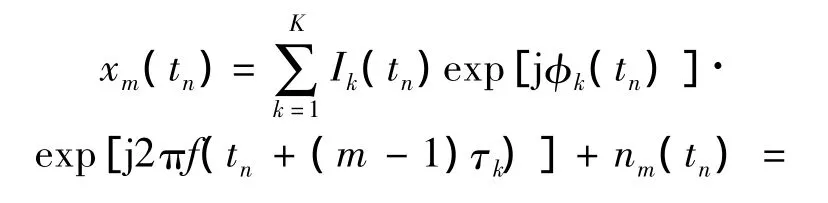
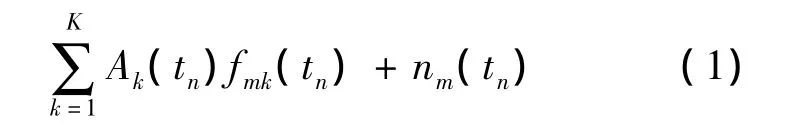
式中，Ik(tn)和φk(tn)分别表示tn时刻第k个信号的幅度和相位;nm(tn)表示tn时刻第m个阵元处的附加噪声，n=1，2，…，N 表示快拍数，m=1，2，…，M表示阵元数.本文的目的是估计信号的方位 Θ =(θ1，θ2，…，θk)T，而对信号的包络 A－={Ak(tn)，∀k，n}和噪声的方差不感兴趣.

由 Bayesian 理论可知，信号方位 Θ =(θ1，θ2，…，θk)T的后验概率密度函数为

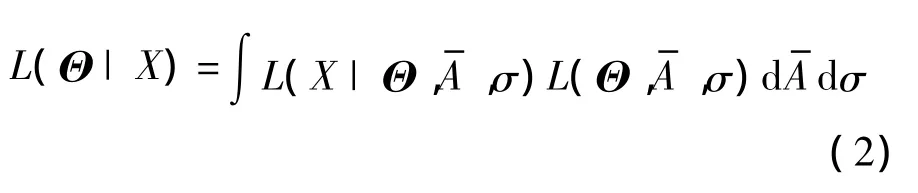
文献［5］提出采样数据正交化算法解决式(2)的积分问题，首先将N次快拍数据分成Nb块，每块有N/Nb=nb个快拍数据.对每一个数据块进行正交化，对于第s个数据块有

λk和ek= ［e1k，e2k，…，eKk］T分别是矩阵 F 的特征值和特征向量，F是K×K维的矩阵，其元素定义为

式中

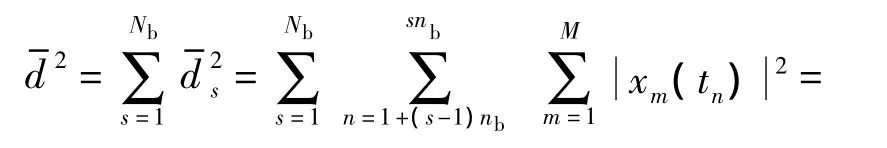
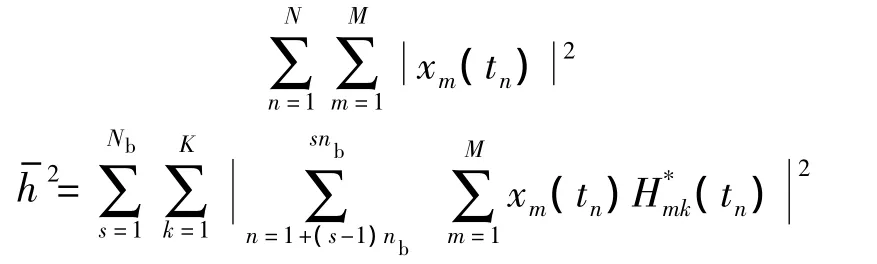
从式(5)可以看出，这是一个关于Θ的高维非线性的多峰值函数，要求它的全局最大值对应的方位角，通过对后验概率密度进行K维网格搜索得到全局最大峰值，计算量非常大，如果计算一个网格点的后验概率密度的计算量为Δ，那么K维的计算量为ΔK.所以尽管Bayesian方位估计方法的估计精度很高，但是其巨大的计算量是其实际应用的最大障碍.

2 基于蚁群算法的Bayesian方法

首先给出ACO-Bayesian方法的流程图如图1所示.

图1 ACO-Bayesian方法流程图Fig.1 Flow chart of ACO-Bayesian method

由于在文献［15］中已对蚁群算法的步骤有了详细的介绍，这里仅作原理性阐述.

2)根据转移概率更新候选解.

满足迭代循环条件时，每只蚂蚁以转移概率p(由式(6)计算)在整个搜索空间中选择一组解Θl(每次迭代每只蚂蚁只需选择一次)，然后构造以选中解为均值，档案表中所有解与选中解的平均距离为标准差(用信息素挥发系数对其进行修正)的高斯核函数如式(7)，利用该高斯核函数对档案表中的所有解进行高斯核抽样得到候选解.

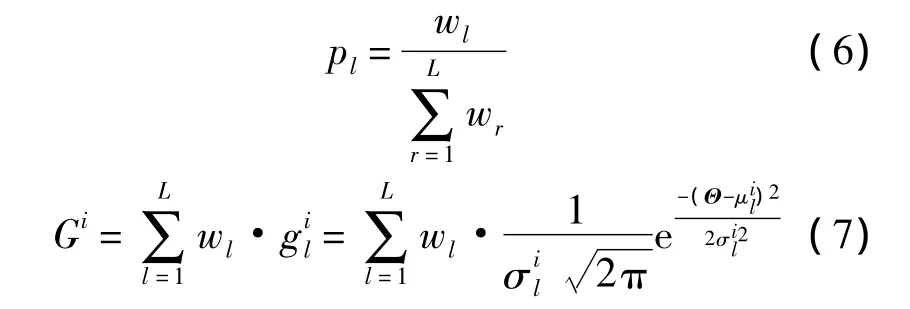
式中，Gi是对整个搜索空间Θ进行一次高斯核抽样值;wl(l=1，2，…，L)即是步骤1)计算的每一组解对应的权值，L是搜索空间的抽样个数;μil即是选中解;σil为用信息素ξ修正的整个搜索空间所有解与当前选中解的平均偏差.对K维搜索空间有

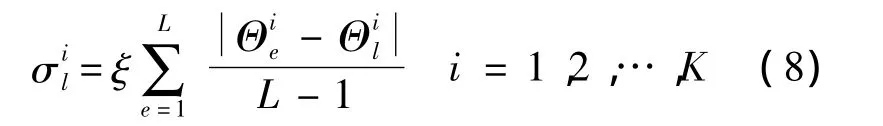
其中Θil表示当前选中解的第i个分量.

3)根据候选解更新搜索空间.

计算候选解对应的目标函数值，并与档案表中的第1组解进行比较，若大于第1组解，则用候选解替换最后一组解(即目标函数值最小的解)，同时给这个新添加的解赋权值，最后对新产生的搜索空间按照目标函数值f从大到小重新排序;若小于第1组解，则不作调整.

4)得到方位估计值.

给定一个精度δ，若连续5次的方位估计值与前一次迭代结果的差值均小于δ，则迭代结束，方位估计结果为最后5次的迭代结果的均值.不满足迭代结束条件转步骤2).

3 仿真结果与性能分析

计算机仿真中采用均匀线列阵，阵元个数为12，采样频率为120 kHz，100次快拍，两目标入射方位角分别为±2°，归一化夹角为α=0.4756.

3.1 目标分辨概率和估计性能分析

1)两目标信噪比为0 dB时，Bayesian方法后验概率分布曲面如图2所示，图3(a)和图3(b)分别是其二维等高线图和峰值点附近的放大图.可以清晰地看出Bayesian方法的后验概率分布曲面只有一个全局最大值点，该点对应的两个角度就是两目标方位的估计值，Bayesian方法是一个非线性的多维最优化的问题.

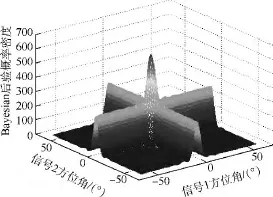
图2 后验概率曲面Fig.2 Curved surface of posteriori probability

图3 二维等高线图和峰值点附近放大图Fig.3 2-dimension contour and enlarged drawing near peak value points

2)ACO-Bayesian方法方位估计结果与迭代次数的关系曲线(SNR=0 dB)如图4所示，可以看出，在信噪比为0 dB的时候，ACO-Bayesian方法有优良的收敛性，可以收敛到最优解.

图4 收敛性分析Fig.4 Convergence analysis

3)分析ACO-Bayesian方法的估计性能，并与Bayesian，MUSIC和MNM方法作对比实验，实验中参数设置如下:T=2，L=100，q=0.1，ξ =0.01，δ=0.001，［θa，θb］=［－ 60°，60°］，做100次Monte Carlo实验，图5是4种方法的分辨概率，可以看出ACO-Bayesian方法的分辨能力与Bayesian相当，优于MUSIC和MNM方法;图6和图7分别是信号1和信号2的估计均方根误差，为了更好地对几种方法的分辨精度进行对比，将由于信噪比过低MNM和MUSIC方法不能成功分辨时的误差标记为10，此时并不是指均方根误差为10，可以看出ACO-Bayesian方法估计性能明显优于MUSIC和MNM方法，信噪比高于 －12 dB时，ACO-Bayesian和 Bayesian方法的估计性能相当.

图5 分辨概率比较Fig.5 Resolution probability comparison

图6 信号1的均方根误差Fig.6 RMSE(root mean squared error)of signal 1

图7 信号2的均方根误差Fig.7 RMSE(root mean squared error)of signal 2

3.2 计算复杂度分析

如果计算一个网格点的后验概率密度的计算量为Δ，则Bayesian方法的计算复杂度为JB=［(θb－ θa)/s］P× Δ，其中，［θa，θb］和 s分别为Bayesian方法的角度搜索范围和搜索步长;而ACO-Bayesian方法的计算复杂度约为JAB≈(P×IP+L+CP×IP)×Δ，其中 P，IP，L分别为 ACOBayesian方法的信号个数、迭代次数和搜索空间抽样个数.对比Bayesian方法的P维搜索，ACOBayesian方法使用高斯核概率抽样技术，P×IP+L小于Bayesian方法P维搜索空间的网格数，而CP是ACO-Bayesian一次迭代高斯核概率抽样的计算量，远远小于P×IP+L.

下面通过仿真对ACO-Bayesian方法的计算量进行分析，仿真模型和参数设置与第3节相同，做50次Monte Carlo实验，表1给出了不同信噪比条件下ACO-Bayesian方法收敛到方位真实值附近所需要的平均迭代次数

表1 不同信噪比条件下ACO-Bayesian方法的平均迭代次数Table1 Mean iteration times of ACO-Bayesian method in different SNR(signal to noise ratio)condition

以信噪比为－5 dB为例，Bayesian方法和ACO-Bayesian的计算复杂度分别为JB=［(θbθa)/s］K× Δ =57600× Δ，JAB≈(T ×IK+L+CK×IK)×Δ=4114.3×Δ.由以上仿真结果可以看出，ACO-Bayesian方法保持了Bayesian方法的估计性能，且计算量大约是Bayesian方法的1/14，大大降低了运算量.

4 水池实验验证

依托20×8×7 m3大型消声水池(如图8所示)开展高分辨方位估计实验对本文的快速方法进行验证，高分辨实验框图如图9所示.

图8 大型消声水池Fig.8 Noise elimination water tank

实验中采用6阵元均匀线列阵，系统采样频率为 122880 Hz，波束宽度约为 16.9°，利用单源数据，按照15 dB信噪比合成夹角为不同波束宽度的双源信号.快拍数为4 000，统计10次，方位估计结果如表2所示.可以看出，ACO-Bayesian最大后验概率方位估计快速方法的均方根误差与原方法相比，略有增加，但仍能正确估计出目标的方位，保持了原方法的高分辨能力，能正确估计夹角为1/5波束宽度的两目标.

图9 高分辨水池实验框图Fig.9 Diagram of high resolution water tank experiment

表2 不同归一化夹角情况方位估计结果Table2 DOA(direction of arrival)in different normalized angle

5 结论

Bayesian高分辨方位估计方法性能十分优越，但该方法理论复杂，本文针对该方法由于多重积分和多维非线性搜索而导致的计算量大、难以工程应用的问题，将连续蚁群算法与Bayesian方位估计方法相结合，提出了一种基于连续蚁群算法的Bayesian(ACO-Bayesian)方位估计新方法，给出了完整的理论过程，并进行了仿真性能分析和水池实验验证.仿真结果表明，ACO-Bayesian方法在保持Bayesian方法优良性能的同时，把Bayesian方法的计算量从((θb－θa)/s)K×Δ减少到(T×IK+L+CK×IK)×Δ，显著减少了计算复杂度，水池实验结果表明，ACO-Bayesian方法能正确估计夹角为1/5波束宽度的两目标，从而为Bayesian方位估计方法的工程应用提供了一种新方法.

References)

［1］ 冯西安.水下目标高分辨方位估计技术研究［D］.西安:西北工业大学，2004.Feng X A.Study on the high resolution DOA estimation techniques of underwater targets［D］.Xi’an:Northwestern Polytechnical University，2004(in Chinese).

［2］ Tadaion A A，Derakhtian M，Gazor S，et al.A fast multiplesource detection and localization array signal processing algorithm using the spatial filtering and ML approach［J］.IEEE Transactions on Signal Processing，2007，55(5):1815-1827.

［3］ Chen C E，Lorenzelli F，Hudson R E，et al.Stochastic maximumlikelihood DOA estimation in the presence of unknown nonuniform noise［J］.IEEE Transactions on Signal Processing，2008，56(7):3038-3044.

［4］ Vorobyov S A，Gershman A B，Wong K M.Maximum likelihood direction-of-arrival estimation in unknown noise fields using sparse sensor arrays［J］.IEEE Transactions on Signal Processing，2005，53(1):34-43.

［5］ Huang J G，Chen J F，Liu C M，et al.Bayesian approach to high resolution direction-of-arrival estimation［C］//Proceeding of the Fourth International Conference on Signal Processing.Piscataway，NJ:IEEE，1998:377-380.

［6］ Li X，Huang J G.Bayesian high resolution DOA estimator based on importance sampling［C］//Proceeding of Oceans 2005-Europe.Brest，France:Institute of Electrical and Electronics Engineers Computer Society，2005:611-615.

［7］ Djuric P M，Li H T.Bayesian spectrum estimation of harmonic signals［J］.IEEE Signal Processing Letters，1995，2(11):213-215.

［8］ Viberg M，Swindlehurst A L.A Bayesian approach to auto-calibration for parametric array signal processing［J］.IEEE Transactions on Signal Processing，1994，42(12):3495-3507.

［9］ Dorigo M.Optimization，learning and natural algorithms［D］.Italy:Dipartimento di Elettronica，Politecnico di Milano，1992.

［10］ Socha K，Dorigo M.Ant colony optimization for continuous domains［J］.European Journal of Operational Research，2008，185(3):1155-1173.

［11］ Dorigo M，Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem［J］.IEEE Transactions on Evolutionary Computation，1997，1(1):53-66.

［12］ Costa D，Hertz A.Ants can colour graphs［J］.Journal of the Operational Research Society，1997，48(3):295-305.

［13］ Gagne C，Price W L，Gravel M.Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence-dependent setup times［J］.Journal of the Operational Research Society，2002，53:895-906.

［14］ Corne D，Dorigo M，Glover F.New ideas in optimization［M］.London，UK:McGraw-Hill，1999:63-76.

［15］ 焦亚萌，黄建国，韩晶.基于连续蚁群优化算法的小快拍加权子空间拟合快速算法［J］.电子与信息学报，2011，33(4):972-976.Jiao Y M，Huang J G，Han J.Continuous ant colony optimization based weighted subspace fitting fast algorithm for DOA estimation with few snapshots［J］.Journal of Electronics ＆ Information Technology，2011，33(4):972-976(in Chinese).