任意波形失真度的一种评价方法

孙璟宇，王中宇，梁志国

(1.北京航空航天大学 仪器科学与光电工程学院，北京100191;2.北京长城计量测试技术研究所，北京100095)

在波形测量中，实际获取的信号与原始信号(或期望的信号)的一致性是首要关注的问题，否则测量结果的可信性将受到质疑.通常，对于“简单”的波形，二者的一致性可能通过这些波形的典型参数来描述，例如波形的幅度、频率、时间或相位偏移、幅度偏移等，更进一步地，包括波形的“面积”(如有效值)等参数;但对于复杂波形来说(例如一般意义上的“任意波形”)，这些参数可能不具有“典型”意义(例如噪声的幅度)，或者无法进行定义(例如噪声的频率)，抑或不具有校准的唯一性意义(例如具有相同有效值的两个波形不能推断两个波形一致).而从人们的主观感受出发，波形的“失真度”却可以反映两个波形之间不一致的程度.

通常，人们定义了正弦波形的失真度指标，用来衡量其谐波分量的大小［1］，并有大量的文献对此进行了研究［2-11］;在某些文献中，脉冲信号的失真也被定义和提及［12-13］.而对于其他波形，特别是一般形式的任意波形，为了表征测量波形与原始波形的一致性，人们也尝试定义了相应的失真度指标，并给出了测量方法［14］.本文则站在对任意波形校准的立场上，就任意波形失真度的评价问题展开讨论.

1 任意波形失真度的定义与评价前提

1.1 任意波形失真度的定义

文献［14］中给出了任意波形总失真度的定义:周期信号实际波形与其最优期望波形间残差的有效值和最优期望波形交流分量有效值之比.即，对于周期为T的已知信号x(t)，其实际波形函数为 y(t)，存在 G，Q，t0∈R，且

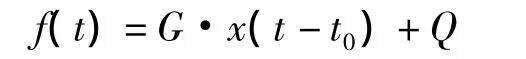
使得

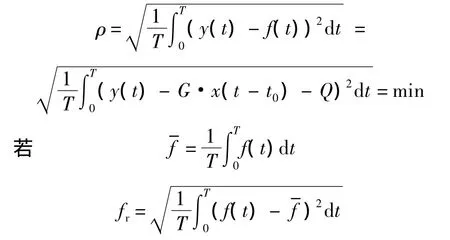
则y(t)相对于其最优期望波形的总失真度DT定义为

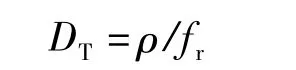
其中，t0为y(t)与x(t)之间的时间延迟;G为波形(幅度)比例因子;Q为波形(幅度)位置偏移量;x(t)为期望波形;f(t)为最优期望波形;为最优期望波形的均值;fr为最优期望波形交流分量的有效值;ρ为y(t)与f(t)之间残差的有效值，表述波形失真.

1.2 任意波形失真度评价的基本前提与假设

为了进行任意波形失真度的评价，有如下的基本前提与假设:

1)谈论到任意波形，人们通常的理解是“任意”给定的波形，或者按照人们的意志“随意”给定的波形.这在通常意义下是对的，也就体现了“任意”性.但谈到对于任意波形的校准，这样的任意显然是行不通的，因为假如人们事先对于所要校准的任意波形一无所知，则校准根本无从谈起.因此，谈到对任意波形的校准，事先必须已知被校准任意波形的模型或参数，然后才能针对这一模型或参数进行校准.

为此，在物理可实现的情况下，周期为T的周期性任意波形一般可以表示为如下形式:

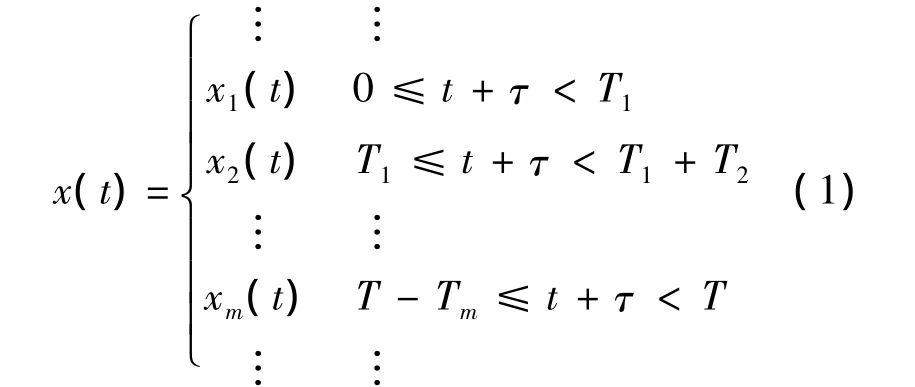
其中，τ为一个实数，代表与t=0时刻相对应的值在曲线函数中的位置;波形在一个周期内可以分割为m段，每段的函数规律和占用的时间比都是严格已知的.

2)本文后续的讨论，均认为研究的任意波形是周期性的.实际上，对于“单次”的任意波形，可以通过周期延拓的办法将其拓展为周期波形，因此不影响相应的讨论过程与结论的得出.

3)用于评价的采样设备的参数或性能指标已知.包括采样使用的采样速率、有效位数、量程等，以及相应参数的不确定度.

2 任意波形失真度评价的过程

任意波形失真度评价的过程，简单地来说，需要使用数据采集系统、数字示波器等波形采样设备获得任意波形，然后对采集到的实际波形与已知任意波形进行比较，从而给出波形的失真度.具体过程如下:

1)对于已知模型的目标任意波形，选取采集系统适当的量程(一般使任意波形的峰峰值达到其80% ～90%)、采集速率rs(根据采样定律，理论上采样速率应高于被校任意波形最高谐波频率的2倍;实际中根据需要选择可接受的将被忽略的最高谐波频率)进行采样，获得相应的采样序列 y(k)，k=1，2，…，m.

2)由于此时采集的y(k)相对于式(1)所示目标波形的“初始位置”一般不会一致，因此需要将目标波形进行相应的平移，亦即对目标波形延迟τ0得到 x(t－τ0)，使二者在起始时间上“对准”.这一过程，就是要对目标波形x(t)延迟时间τ，使用相同的采样速率rs进行采样得到x(k)，并与实际采样序列y(k)进行非线性最小二乘拟合运算，找出“最佳的”延迟时间τ0，并得到此时的目标波形 x0(t)的采样序列为 x0(k)，k=1，2，…，m.

此时，由于实际采集序列y(k)与目标序列x0(k)存在幅度的比例关系(由于采集系统传递函数的模不为1，亦即对于波形采集存在幅度的“放大”或“缩小”)，因此以下证明，即使二者存在这种幅度的比例关系，上述最小二乘拟合运算的结果也是正确的.

为此，假设y(k)对应的连续波形y(t)与目标波形x(t)恰好“对准”，亦即

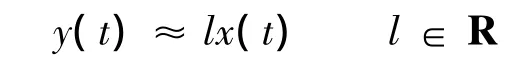
则

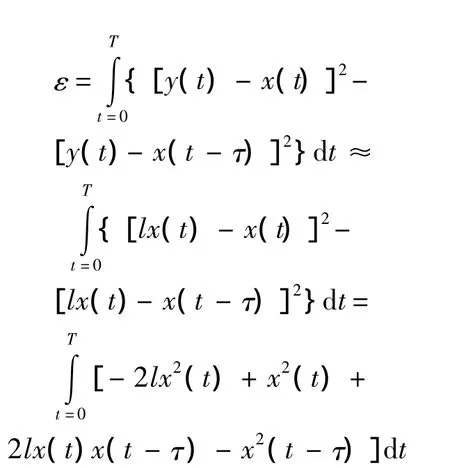
注意到，由于x(t)以T为周期，因而有

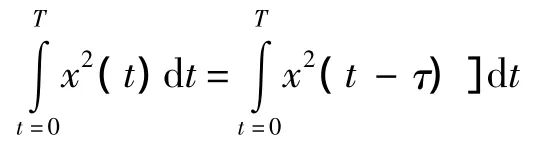
于是

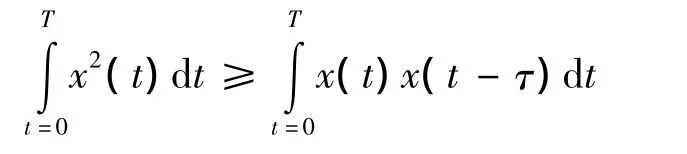
于是就有ε≤0，也就是说，即使实际测量的信号幅度按比例进行了缩放，但在“相似对齐”的情况下，其与目标信号的误差平方和也是最小的.

3)为叙述方便，以下将x0(t)简记为x(t);并令与测量波形y(t)最小二乘最优的期望函数为f(t)=G·x(t)+Q.即，选取合适的G与Q，使得

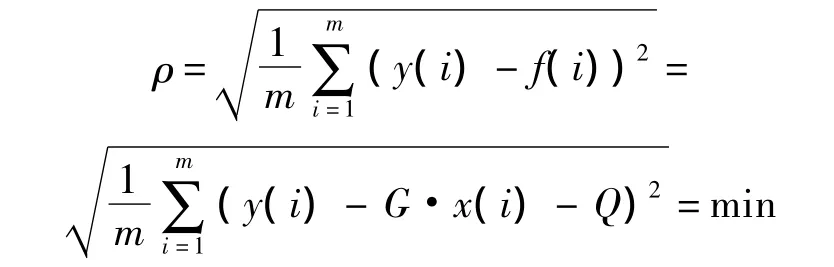
则有

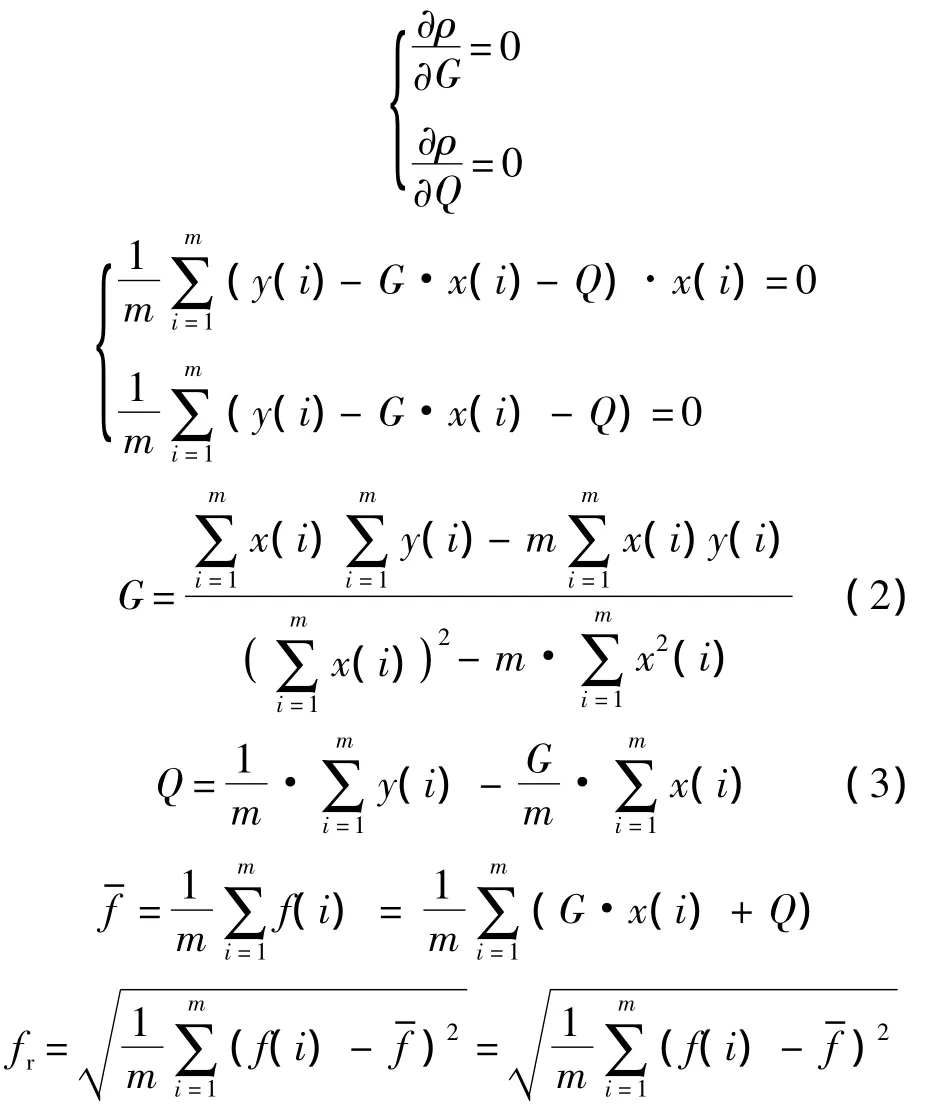
测量数据的总失真度:

修正掉测量设备的A/D位数DB的影响后，则信号 y(t)的总失真度为［15］

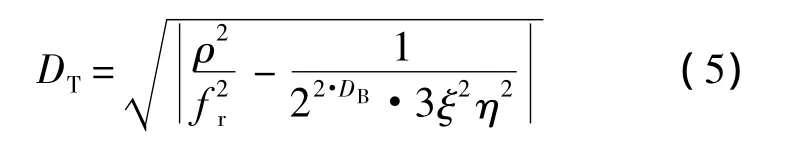
式中，ξ为周期信号交流有效值和峰值之比;η为周期信号峰峰值与测量设备量程之比.

3 实验验证

为了验证上述评价过程的可行性，选取典型的心电图波形进行实验，如图1所示.为简化验证过程，只选取心电波形中包含P波和QRS波的P-R间期和 QRS时限.对此建立函数模型如下(单位:mV;周期 0.4 s，峰值 0.7 mV，峰峰值1.1 mV):

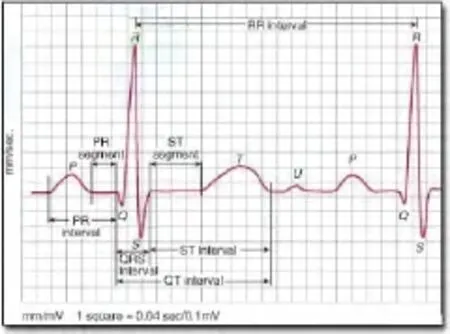
图1 正常心电图示意图Fig.1 Sketch of normal electrocardiogram

1)按照上述评价过程，首先使用Tektronix AWG20212任意波发生器模拟产生该波形(实际模拟发生时将幅度放大3 000倍，即:峰值2.1 V，峰峰值3.3 V)，并使用Tektronix TDS7104数字存储示波器进行采集，获得采样波形y(k)，见图2中序列1.

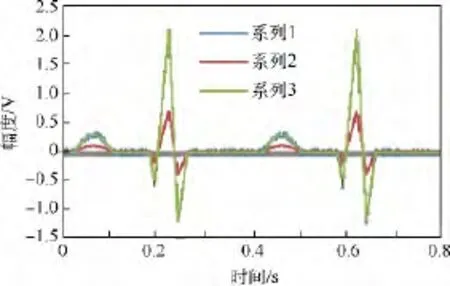
图2 采样波形与拟合序列Fig.2 Sample waveform and fit waveform

2)使用相同的采样速率采样x(t－τ)，并与上述采样波形进行非线性最小二乘拟合，得到拟合波形x(t－τ0)，如图2中序列2.

3)构造f(t)=G·x0(t)+Q，并与y(k)进行最小二乘拟合;按照式(2)、式(3)得:G=2.9952，Q= －0.0167 V，如图2中序列 3.从而根据式(4)计算:

DTs= ρ/fr=0.02789/0.4153=6.7%

4)修正测量设备的A/D位数DB的影响(使用数字存储示波器的量程为5V，DB的位数为6.1 位)，根据式(5)计算:

4 结论

任意波形的失真度，能够反映被测信号中“无用”或“有害”信号的大小，从而反映信号的品质.对其进行评价，在诸如军事、工业测控、医疗、科学实验与仿真等领域具有特别的需求.从本文的讨论中，可以得出以下结论:

1)文献［14］所描述的任意波形失真度的一般定义具有广泛的适应性，可以从时域角度定量描述被测波形与其期望波形之间的差异，并且在现实中是完全可以实现的.

2)经过理论推导，可以使用简便的方法，通过波形非线性拟合，得到被测任意波形的最佳拟合波形，从而得出被测波形的失真度.

3)由于该方法使用时域计算就能完成整个评价过程，对数据采样没有整周期或者同步的要求，可以完全避免频谱分析方法所固有的栅栏效应或频谱泄漏带来的评价误差问题，从而使所有采集到的数据均得到有效利用.同时，也因为避免了繁琐的频域计算与时频域转换过程，而且步骤简单易行，甚至在目前的技术条件下，使用普通的个人计算机就能够达到实时评价的程度.

References)

［1］ 苏皖生，郭允晟.关于正弦波失真表示方法的讨论［J］.计量学报，1986，7(2):123-127.Su W S，Guo Y S.On the methods to express the distortion of a sinewave［J］.Acta Metrologica Sinica，1986，7(2):123-127(in Chinese).

［2］ 梁志国，朱济杰，孙璟宇.正弦信号源波形失真的一种精确评价方法［J］.计量学报，2003，24(2):144-148.Liang Z G，Zhu J J，Sun J Y.A precise evaluation method for the distortion of sinusoidal sources［J］.Acta Metrologica Sinica，2003，24(2):144-148(in Chinese).

［3］ Bracale A，Caramia P，Carpinelli G.Adaptive Prony method for waveform distortion detection in power systems［J］.Electrical Power and Energy Systems，2007，29(5):371-379.

［4］ 王慧，刘正士.基于希尔伯特-黄变换的信号总失真度评价［J］.华中科技大学学报:自然科学版，2008，36(增刊 1):302-305.Wang H，Liu Z S.The evaluation for total distortion of signal based on Hilbert-Huang transformation［J］.Journal of Huazhong University of Science and Technology:Nature Science Edition，2008，36(S1):302-305(in Chinese).

［5］ 孙伟，郭宝龙，陈龙.一种新的音频分析系统的实现方法［J］.仪器仪表学报，2009，30(11):2249-2254.Sun W，Guo B L，Chen L.New solution to signal generator and distortion analyzer［J］.Chinese Journal of Scientific Instrument，2009，30(11):2249-2254(in Chinese).

［6］ Morsi W G，El Hawary M E.A new reactive，distortion and nonactive power measurement method for nonstationary waveforms using wavelet packet transform［J］.Electric Power Systems Research，2009，79(10):1408-1415.

［7］ Claudionor Francisco Nascimento，Azauri Albano Oliveira Jr，Alessandro Goedtelc，et al.Harmonic distortion monitoring for nonlinear loads using neural-network-method［J］.Applied Soft Computing，2013，13(1):475-482.

［8］ 路程，张晓林，李铀.无线通信非线性失真仿真器的设计与实现［J］.北京航空航天大学学报，2011，37(5):528-533.Lu C，Zhang X L，Li Y.Design and implementation of a simulator for wireless communication nolinear disrortion［J］.Journal of Beijing University ofAeronauticsand Astronautics，2011，37(5):528-533(in Chinese).

［9］ Ugur M，Cekli S，Uzunoglu C P.Amplitude and frequency detection of power system signals with chaotic distortions using independent component analysis［J］.Electric Power Systems Research，2014，108:43-49.

［10］ Chen Z，Geng G，Yin F，et al.A pre-distortion based design method for digital audio graphic equalizer［J］.Digital Signal Processing，2014，25:296-302.

［11］ Pasovic M，Danilouchkine M，Matte G，et al.Broadband reduction of the second harmonic distortion during nonlinear ultrasound wave propagation［J］.Ultrasound in Medicine ＆ Biology，2010，36(10):1568-1580.

［12］ GB 9317—1988脉冲信号发生器技术条件［S］.北京:电子工业出版社，1990.GB 9317—1988 The specifications of pulse signal generators［S］.Beijing:Publishing House of Electronics Industry，1990(in Chinese).

［13］ Shi X M，Yeo K S，Ma J G，et al.Distortion of pulsed signals in carbon nanotube interconnects［J］.Microelectronics Journal，2007，38(3):365-370.

［14］ 梁志国，孙璟宇，孟晓风.目标序列已知的周期波形总失真度的测量［J］.计量学报，2008，29(2):172-177.Liang Z G，Sun J Y，Meng X F.Evaluation of the total distortion of periodic arbitrary waveform signals base on the target waveform series known［J］.Acta Metrologica Sinica，2008，29(2):172-177(in Chinese).

［15］ 梁志国，朱济杰.量化误差对周期信号总失真度评价的影响及修正［J］.仪器仪表学报，2000，21(6):640-643.Liang Z G，Zhu J J.The correction of the influence of quantization error to the evaluation of the distortion of periodic signal［J］.Chinese Journal of Scientific Instrument，2000，21(6):640-643(in Chinese).