职业能力测评中评分者信度FINN系数与ICC的计算与MATLAB实现

钟 韬，魏庆曜

(四川交通职业技术学院，四川 成都 611130)

职业能力测评中评分者信度FINN系数与ICC的计算与MATLAB实现

钟 韬，魏庆曜

(四川交通职业技术学院，四川 成都 611130)

对FINN系数与组内相关系数ICC进行研究和分析，详细介绍了FINN系数与组内相关系数ICC的数学原理与计算方法.将FINN系数与组内相关系数应用于职业能力测评，结果显示FINN系数更能得到较好的信度值.而ICC更依赖评分点平均值的方差，在职业能力测评中容易得到较低的信度值，从而测量不出重要的信度.文章例解了FINN系数与组内相关系数ICC的MATLAB计算程序.

FINN系数；组内相关系数ICC；评分者信度

随着我国职业教育课程和教学改革的深入，如何对学生的职业能力进行有效的评价成为大家关注的一个重点问题.在对学生的某些表现性进行评估的时候，要求评分者之间的评判标准是一致的.特别是当表现性评价的结果将用于重要决策时，为了保证评价的客观性以降低决策的风险，我们应该对评分者信度进行严密的考察.

对于学生职业能力测评中评分者信度的计算，目前缺少现成的统一的方法，此文旨在探讨FINN系数和组内相关系数(intra-class correlation coefficient，简称“ICC”)这两种方法.FINN系数的数学模型由心理学教授R.H.FINN在1970年提出，它非常适用于等级制的表现性评价问题，但国内文献对该模型的解释和研究非常缺乏.另一方面，对于一般的表现性评价问题，ICC虽然是一个较好的方法，但是否适用于职业能力测评这类实证问题仍有待考证.

此文旨在对FINN系数与ICC进行深入的研究和分析，剖析FINN系数与组内相关系数ICC的数学原理与计算方法；给出了FINN系数与组内相关系数ICC的MATLAB的计算程序；并以职业能力测评中的能力模型和测评数据为背景，分别使用FINN系数与ICC(组内相关系数)对职业能力测评数据的评分者一致性进行计算，最后对计算的结果进行了系统的分析和整理，指出了应用FINN系数与组内相关系数ICC计算评分者信度需要注意的问题.此文为高校职业能力测评的研究者计算评分者信度提供了依据和计算方法.

1 FINN系数的概念与计算

1.1 FINN系数的概念

该模型假设:如果评判结果的实际的方差Variance(observed)为零，代表所有评分者达成完全协议或具有完全的可靠性，可靠性为1.另一方面，如果只是完全随机的对测评对象作出评级，这种情况下评级的概率分布将满足均匀的离散分布，这时的方差我们称之为预期的方差Variance(expected)，此时的可靠性为0.

1.2 FINN系数的计算

1.2.1 构造检验的统计量:

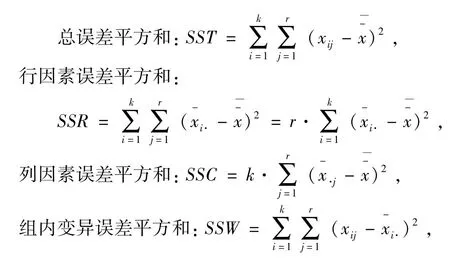
SST的自由度为:kr-1，

SSR的自由度为:k-1，

SSC的自由度为:r-1，

《天鹅》是大提琴独奏曲，旋律纯净质朴，给人带来的是美的享受。在欣赏这首乐曲时，教师先让学生聆听音频，并给出了基本要求：仔细聆听乐曲，自己总结一下，看乐曲速度、情绪、风格等方面都有什么特点？学生拿到任务后，都潜心聆听，并自发展开讨论。经过一番学习研究，学生都能够给出自己的见解。有学生认为，这首乐曲运行速度比较缓慢，旋律中充满沉静与思考，仿佛看到了朦胧的月色下一只天鹅在水面翩翩起舞，给人带来的感觉是舒适、静谧和遐想。也有学生说，这首乐曲是独奏形式展现的，增加了太多思考的内容，给人以心灵的触动。

SSW的自由度为:k·(r-1)，

SSE的自由度为:(k-1)·(r-1).

1.2.4 FINN系数的计算公式:

2 组内相关系数的概念与计算

2.1 组内相关系数的概念

生物统计学家James Aharris教授[2]在1912年提出来组内相关系数这一概念，并将其应用于流行病学和遗传学等自然科学领域.目前也有部分学者将其应用于各种社会科学定量研究中.如管理学、心理学等学科中的信度评估[3-5]，经济学、社会学和教育学中成员间各种社会经济指标的相似程度.同时它还是统计学中很多高级模型的基础，如判断是否需要建立多层线性的数学模型.

组内相关系数(ICC)是衡量和评价观察者间信度的量化指标之一.1966年Bartko首次将它运用于测量和评估信度的大小[6].ICC等于个体的变异度除以总的变异度，它的计算结果介于0～1之间.0代表信度极低，评分结果完全不可信，l表示信度极高，评分结果完全可信.一般情况下，ICC低于0.4代表信度较差，大于0.75则代表信度良好.当ICC应用于定量资料时，则要求较高的信度值[7].

2.2 组内相关系数的计算

根据研究目的的不同，ICC可划分为各种不同的类型，用于估计不同总体参数.因此对同一组数据，不同类型的ICC计算结果是不相同的.在职业能力测评中，由于既要考虑行因素的随机效应，又要考虑列因素的随机效应，因此我们选用了两因素随机效应模型(twoway random effects mode1)[6]:

式中，μ:所有观察数据的总均数，为常数；ri:行因素(即被测试者)的随机效应，服从符合独立正态分布，均数为0，方差为σ2r；cj:列因素(即被测试者)的随机效应，服从独立正态分布，均数为0，方差为σ2c；eij:随机残差的效应，服从独立正态分布，均数为0，方差为σ2e；所有效应互相独立.

又因为研究设计(比如KOMET项目)在进一步研究中是使用单个评分者评分，而且需要考虑评分者系统误差，因此我们选择Single Absolute agreement[6]类型:

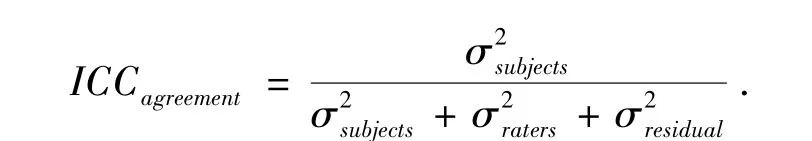
综上所述，我们选择ICC(A，1)用于职业能力测评中评分者信度的计算，其计算公式如下:

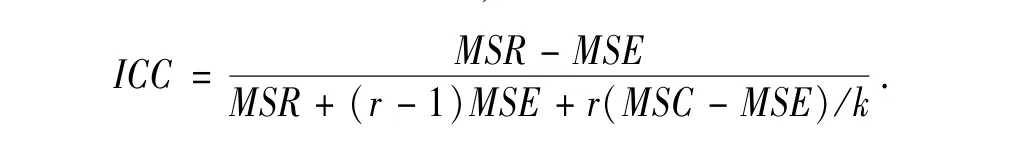
若选用Single consistency[6]类型，则计算公式如下:

3 FINN系数与组内相关系数ICC的MATLAB实现

4 FINN系数与组内相关系数在职业能力测评中的实例应用

表1数据是在一次针对汽修专业学生的职业能力测评中，关于应对“发动机水温过高”故障处理的评分数据.由17位教师(评分者)针对40个能力点进行的评分.

表1 “发动机水温过高”故障处理评分数据(初测)Table 1 Score data of disposing"Engine water temperature is too high"(first evaluation)

表2数据是在评分者培训后所进行的测评，评分数据是由与初测相同的17位教师针对40个能力点给出的评分.

表2 “发动机水温过高”故障处理评分数据(复测)Table 2 Score data of disposing“Engine water temperature is too high”(second evaluation)

分别采用FINN(oneway)、FINN(twoway)、ICC (C，1)、ICC(A，1)计算两次测试的评分者信度.计算结果如表3.

表3 两次测评的评分者信度Table 3 The reliability of the two test scores

5 小结

通过对以上结果的分析，我们发现FINN系数获得的评分者信度值相比ICC会比较乐观.计算组内相关系数ICC的方法，是一种较为严格的评价方法，但它存在一个问题，即评分点平均值的一个极小的方差，也会致使ICC“测量不出或测量不出重要的信度”(Wirtz/Caspaper 2002).比如在表3中，利用ICC计算的结果就比较小.虽然这时也可以接受一个较小的ICC值，但却很难确定一个明确的阈值，说明合格与不合格的评分者信度之间的界限在哪里.

在职业能力测评中的实践中，由于普遍采用的是等级评分制，评分结果是离散数据，离散数据本身会丢失一部分信息.又由于不可避免各个评分点的难度存在差异，评分点平均值的方差会导致ICC“测量不出或测量不出重要的信度”.和ICC相比，FINN系数“明显不依赖评分点平均值的方差”(Asendorf/Wallbott 1979).因此，在职业能力这一类测评中适合将FINN系数用作计算评分者信度的标准.

在实际应用中要注意:FINN系数介于0.0～1.0.其中，0.0表示评分者的评分结果之间不存在任何联系；而1.0表示评分者之间既有相同的平均值也有相同的方差.数值越接近1.0，评分结果的评分者信度越高.FINN系数在0.5～0.7表示及格，大于0.7表示良好.在职业能力测评中，只有较高的FINN系数才是令人满意的评分者信度，也就是说，在实践中只有0.7以上的FINN系数才是足够高的.

[1]FINN R H.A Note on Estimating the Reliability of Categorical Data [J].Educational and Psychological Measurement，1970，30:71.

[2]HARRIS J A.The formation of condensed correlation tables when the number of combinations is large[J].The American Naturalist，1912，46 (548):477-486.

[3]曾五一，黄炳艺.调查问卷的可信度和有效度分析[J].统计与信息论坛，2005，6:13-17.

[4]杨奇明，林坚.组内相关系数:定义辨析、估计方法与实际应用[J].浙江大学学报，2013，40(5):509-515.

[5]杨建锋，王重鸣，类内相关系数的原理及其应用[J].心理科学，2008，2:434-437.

[6]余红梅，罗艳虹.组内相关系数及其软件实现[J].中国卫生统计，2011，28(5):497-500.

[7]潘晓平，倪宗瓒.组内相关系数在信度评价中的应用[J].华西医科大学学报，1999，1:62-63.

[8]FISHER R A.Statistical Methods for Research Workers[M].Edinburgh:Oliver and Boyd，1925.

[9]王维，陈青山，刘治民.应用Excel完成组内相关系数ICC的计算和评价[J].中国卫生统计，2008，25(3):314-315.

[10]安娜斯塔西A苏珊娜.心里测量[M].缪小春，竺陪梁，译.杭州:浙江教育出版社，2001:111-129.

[11]黄广杨.教育测量与评价[M].上海:华东师范大学出版社，1993:275-276.

[12]GLEASON J R.Computing intraclass correlations and large ANOVAs [J].Stata technical bulletin，1997，6(35):26.

[13]黄卫石.国家公务员考试面试评分者信度的研究[J].安徽教育学报，1998(3):82-85.

[14]漆书青.现代测量理论在考试中的运用[M].武汉:华中师范大学出版社，1998:78-80.

[15]LYNCH，BRIAN K.Language Assessment and Programme Evaluation [M].UK:Edinburgh University Press，2003:87-88.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Calculation of FINN coefficient and ICC for rater reliability in competence assessment and the MATLAB program

ZHONG Tao，WEI Qing-yao
(SichuanVocational and Technical College of Communications，Chengdu 611130，P.R.C.)

This paper is devoted to researching and analyzing the FINN coefficient and ICC.The concept and calculation method of them were presented in detail.Being applied to the competence assessment，the results show that by using FINN coefficient，people can get better reliability value.Because ICC depends more on the average variance of Score point，it is easy to get low reliability value in competence assessment，so that people can’t detect important reliability in this case.The matlab program is given in this paper.

FINN coefficient；ICC；rater reliability

O213；F241

A

2095-4271(2015)04-0489-05

10.11920/xnmdzk.2015.04.018

2015-05-12

钟韬(1981-)，男，汉族，四川人，讲师，研究方向:应用数学和高等教育研究，E-mail地址:tom_joan＠163.com.

魏庆曜(1956-)，男，汉族，重庆人，教授，研究方向:高等教育研究，E-mail地址:sccdwqy＠163.com.

教育部哲学社会科学研究重大攻关项目(13JZD047-09)；交通运输部科技项目(2012-319-284-310).